农机滑动轴承油膜润滑理论及边界条件的研究*

高宇星 ， 徐武彬 ， 李 冰 ， 赵江南

（1.广西科技大学机械与交通工程学院，广西 柳州 545006；2.广西土方机械协同创新中心，广西 柳州 545006）

0 引言

滑动轴承转子系统在大型农业机械领域中有极为广泛的应用[1-2]。由于滑动轴承圆度误差会导致轴承的油膜几何特征发生变化，从而改变油膜的发散和收敛边界，此时轴承的油膜特性将发生很大的变化，这对旋转机械的工作性能和运行特性有很大的影响，因此与滑动轴承油膜润滑理论及边界条件相关的研究一直是旋转机械研究领域中重点关注的问题[3-5]。

从滑动轴承润滑分析模型的建立到线性和非线性油膜力计算的研究，国内外学者围绕滑动轴承油膜润滑理论及边界条件进行的研究已经取得了一系列进展[6-7]。然而，所开展的轴承油膜润滑分析中也存在着多种问题，如误差信息表达不足、油膜力求解方法的稳定性差以及油膜边界条件选取不合理等，这些问题对滑动轴承的润滑特性均有影响。

滑动轴承油膜润滑理论研究的关键是在适当的边界条件下寻找Reynolds方程及其他控制方程（如能量方程、热变形方程等）的解。由于滑动轴承工作表面的制造误差与油膜厚度在同一量级（μm）上，所以轴承工作表面的制造误差会导致油膜的几何特征发生变化，从而会改变油膜的发散边界和收敛边界[8]。因此，如何确定符合实际的Reynolds方程边界条件将成为滑动轴承润滑理论分析的关键问题。

1 滑动轴承油膜润滑理论的发展和研究现状

滑动轴承油膜润滑理论的核心就是Reynolds方程[9]。该方程是三维Navier-Stokers方程根据油膜润滑的特性忽略方程中的惯性项得到的[10-12]，但是，由于Reynolds方程并不存在任何封闭形式的解，所以该方程的求解成为该领域新的难点。

1904年，德国著名的理论物理学家Arnold Sommerfeld提出了无限长轴承的假设，通过对雷诺方程进行解析求解，最终得到了无限长轴承的油膜压力分布[13]。1953年，Dubois和Ocvirk[14]在长轴承假设的基础上，提出了一种短轴承假设，建立了无限短轴承的解析解。长轴承假设和短轴承假设方法的核心是假设轴承长径比无限大或无限小，从而使Reynolds方程实现降阶可积，并最终求出解析解。但是，在工程领域中使用的滑动轴承转子系统大多是有限长轴承，因此有限长轴承油膜力的计算也成为这一领域重点研究的问题[15]。在1941年，学者Christopherson[16]首次提出运用FDM的方法对雷诺方程进行求解，并采用Southwell松弛法来进行迭代计算，获得Reynolds方程的数值解，他在研究中假定所有负向的压力为0，油膜起始端和末端的压力及压力梯度也均被设为0，而这样的假定实际上便是Reynolds方程的边界条件。1949年，Cameron等[17]基于Christopherson所提出的有限差分法求解了有限长滑动轴承转子系统的雷诺方程，获得了滑动轴承转子系统在稳定状态下的运行特性，并证明稳态特性与实验结果一致。1958年，Raimondi和Boyd[18]通过有限差分法求解得到了轴承油膜压力的数值解，并进一步通过积分法获得了滑动轴承的轴承力。此后，有限差分法得到了较为广泛的运用，并且还在不断地完善和发展。滑动轴承研究的关键是在适当的边界条件下寻找Reynolds方程的解。由于数值方法相对于其他方法而言更易于操作、具有更高的精度。因此，近年来Reynolds方程的求解主要采用数值方法。

随着轴承润滑理论的发展，轴承油膜润滑理论的研究对象越来越复杂，理论中考虑的实际因素越来越全面。Elrod等[19]提出了一种考虑空穴效应的算法，该算法在JFO的边界条件下保证了整个轴承区域内润滑油的质量守恒。Kim等[20]提出了一种TEHD计算模型，该模型考虑了轴承内的热效应和弹性变形效应对油膜特性的影响，被影响的因素主要包括润滑油粘度、油膜的热传导效应及轴承的热传导效应等。Hashimoto等[21]分别在层流和湍流状态下研究了由于磨损造成的轴承的几何变化对滑动轴承动态和静态特性的影响。在1978年，Lund和Thomsen[22]根据有限差分法提出了一种考虑油膜破裂边界的高效算法，能够对不同结构的轴承进行特性预测，如油膜压力分布及轴承的承载力等。本文提出的Reynolds边界条件（又称Swift-Stieber边界条件）也是目前最为常见的轴承润滑边界条件。

2 润滑油膜的形成机理及Reynolds方程

根据摩擦表面之间油膜形成的原理，得到如图1所示的滑动轴承润滑油膜形成机理图。在滑动轴承高速运转的过程中，滑动轴承转子系统在收敛区内可以通过轴承与轴颈之间的相对运动而自动形成润滑油膜，滑动轴承转子系统可以依靠该油膜进行润滑[23]。

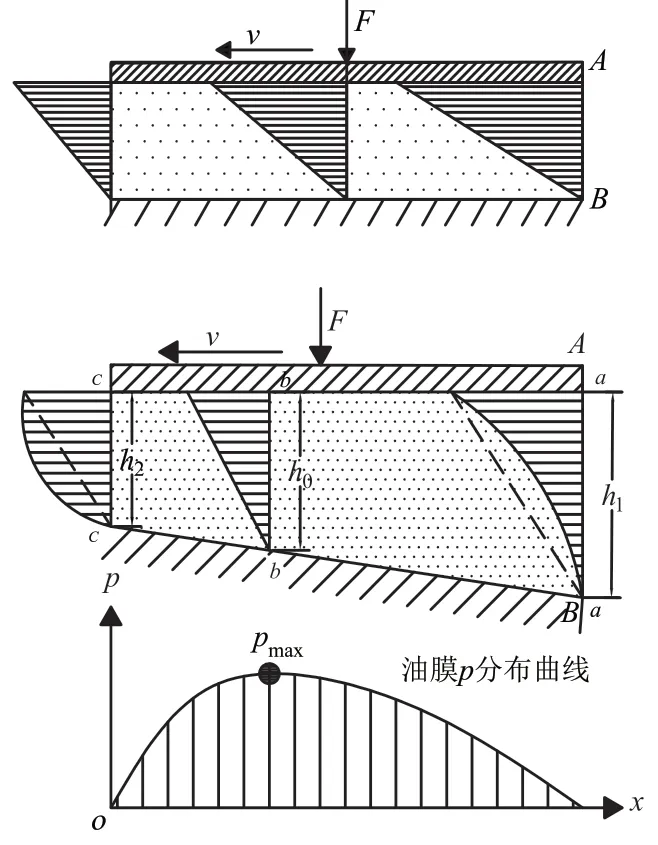
图1 滑动轴承润滑油膜形成机理图

Reynolds对轴承动压油膜的形成机理进行了详细分析，并提出油膜润滑理论的核心是Reynolds方程。该方程可以从理论上计算两个相互滑动表面之间形成的油膜压力，并对轴承的油膜压力分布进行描述。Reynolds方程如公式（1）所示：

方程从左到右的各项分别描述了油膜压力沿轴承圆周方向（记作X轴方向）的压力变化、油膜压力沿轴承轴线方向（记作Z轴方向）的压力变化、流体的动压效应及油膜的挤压效应。

3 求解Reynolds方程的边界条件

在油膜润滑理论的研究中，油膜形成和破裂的边界条件的观点各有不同[24]。目前，工程实际中经常采用的边界条件有：Sommerfeld边界条件[25]；半Sommerfeld边界条件[26]；Swift-Stieber边界条件[27]等。

3.1 Sommerfeld边界条件

该边界条件认为油膜在滑动轴承轴颈圆周360°上的每个位置都存在完整的油膜，并且该润滑油膜在收敛楔与发散楔内可以形成相互对应的正、负压力区域，如图2、图3所示。

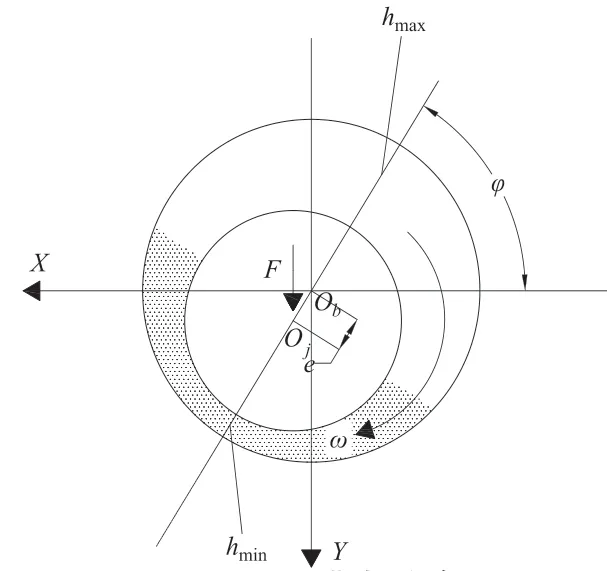
图2 油膜力分布

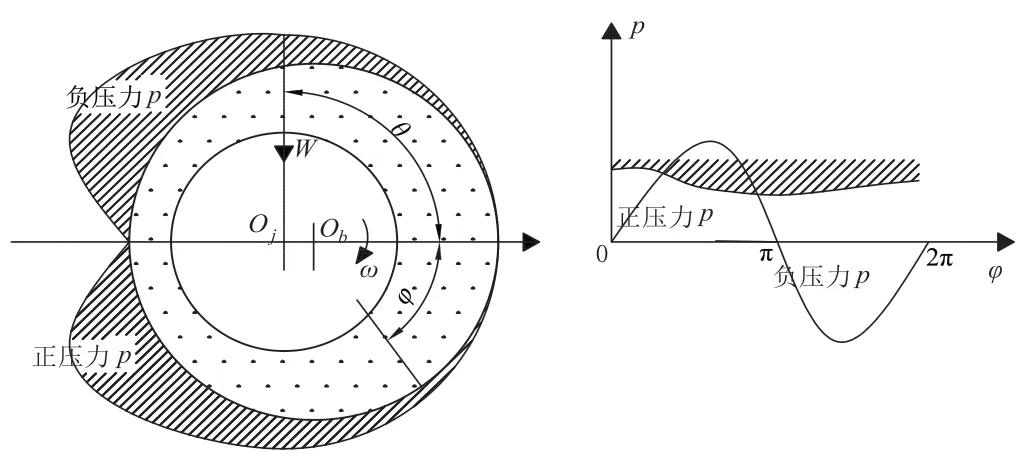
图3 Sommerfeld边界条件

Sommerfeld边界条件示意图如图3所示，在该边界条件下油膜压力沿轴承轴线方向（记作Z轴方向）的压力变化满足周期函数，即p(φ)=f(2π+φ)，Reynolds方程在Sommerfeld边界条件下的求解区间如公式（2）所示：

3.2 半Sommerfeld边界条件

该边界条件认为油膜在滑动轴承运行工作中只承受油膜正压区（0,π）区间内的正压力，而在负压区（π,2π）区间内不承受任何压力。因此，该边界条件下的油膜压力分布假设可以认为是Sommerfeld边界条件下油膜压力p(φ)的简化。

如图4所示，半Sommerfeld边界条件示意图中存在正压区p(φ)，在求解过程中只计算油膜收敛楔正压区p(φ)内的承载力，不考虑负压区内油膜压力的影响，因此Reynolds方程在半Sommerfeld边界条件下进行求解时，设定的求解区间如公式（3）所示：

图4 半Sommerfeld边界条件

3.3 Swift-Stieber边界条件

Swift-Stieber边界条件认为，形成油膜正压区的起止点是从最大轴承间隙hmax开始的，而轴承油膜破裂的边界位置由油膜压力为0以及切向压力梯度为0这两个条件来决定，具体边界区间如公式（4）所示，因此该边界条件也被称为自然破裂边界条件。

Swift-Stieber边界条件示意图如图5所示，认为流体润滑压力的出发点在最大流体润滑油膜处，而且满足油膜的流动连续性。

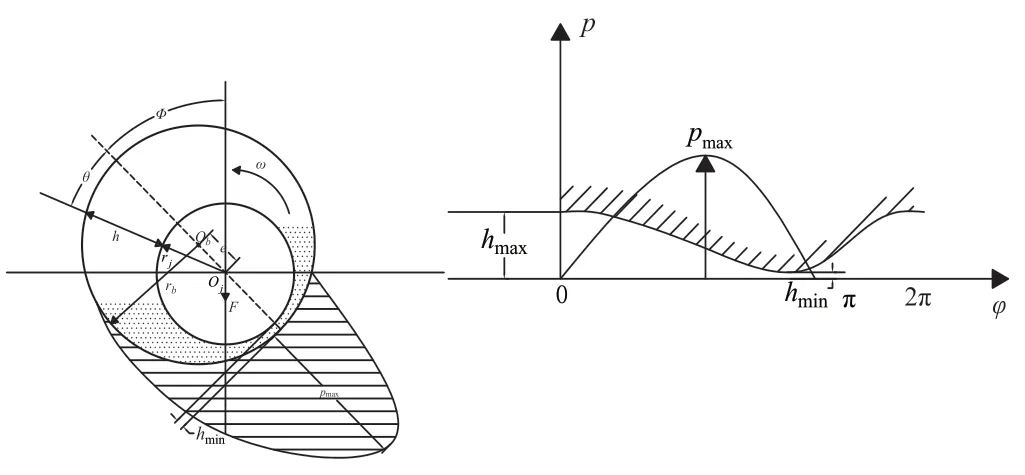
图5 Swift-Stieber边界条件

Reynolds方程在Swift-Stieber边界条件下进行求解时，要求在油膜破裂边界处的油膜压力及其梯度值均为0。因此，设定的求解区间如公式（4）所示：

Swift-Stieber边界条件具有较高的精度和较为方便的施加过程，是目前油膜润滑分析中最为常见的边界条件之一。与上述两种边界条件相比，Swift-Stieber边界条件以油膜区内液体流动的连续性为出发点，符合压力和流量的连续条件。因此，该边界条件在油膜破裂处使用更加合理，符合润滑轴承的实际情况。但是Swift-Stieber边界条件仅适用于理想轴承，且不能保证润滑边界上润滑油的质量守恒。考虑制造误差的影响后，该条件有可能失效，而且不能解释油膜再形成的情况，因此不适用于对误差轴承的理论分析。

3.4 三种边界条件的对比

Sommerfeld边界条件和半Sommerfeld边界条件相对较为简单，在理论推导和精度要求不高的情况下使用较多，但是二者仅考虑在正压区域内的计算，而将负压区域的压力值设定为0，也未考虑空穴区域压力或者是外部大气压压力；Swift-Stieber边界条件在不同的情况下考虑了流体的质量守恒，其压力计算结果和实际情况较为接近，在数值计算中使用较多。

在滑动轴承转子系统实际工作的过程中，由于轴承圆度误差会导致轴承的油膜几何特征发生变化，从而改变油膜的发散和收敛边界，且负压区油膜的破裂会导致油膜在轴颈的圆周表面上不连续，与假设条件相违背，因而传统的边界条件如半Sommerfeld边界条件、Sommerfeld边界条件均不适用于对误差轴承进行润滑特性分析。与这两种传统边界条件相比，Swift-Stieber边界条件要求在油膜破裂边界处的油膜压力及其梯度值均为0，这种边界条件更加符合滑动轴承润滑分析的实际情况。

4 Reynolds方程的求解算例

滑动轴承转子系统是通过改变油膜压力来运行的，作用在轴颈上的非线性油膜力既与轴颈的位置有关，又与轴颈的运动有关，因此可以通过压力场的数值积分得到。

为提高求解精度，在求解油膜压力P的过程中，首先将油膜压力的收敛精度设为1×10-7，并在Swift-Stieber边界条件下对Reynolds方程进行数值求解，最终得到轴颈表面油膜压力P的分布。其中，滑动轴承油膜压力分布图如图6所示。

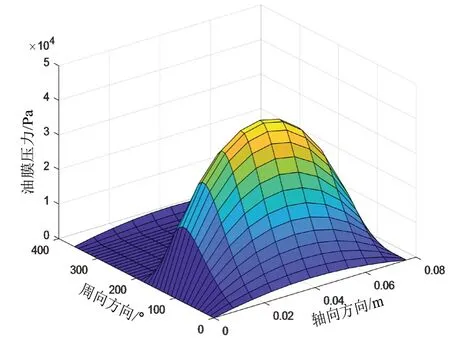
图6 滑动轴承油膜压力分布图

该算例与Ogrodnik[28]给出的油膜压力分布结果的对比图如图7所示，在Swift-Stieber边界条件下求得的压力计算结果与压力分布和实际情况较为接近，说明在Swift-Stieber边界条件下对Reynolds方程进行数值求解具有较高的准确性，可用于后续的研究。

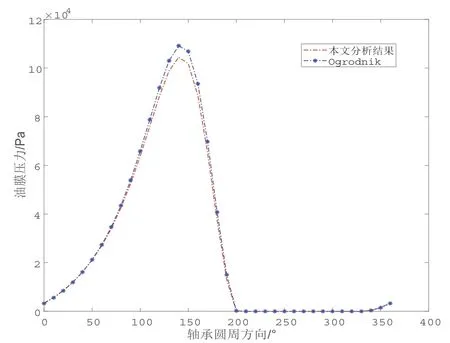
图7 油膜压力结果对比图

在研究圆度误差旋量参数对滑动轴承油膜压力分布影响的过程中，滑动轴承转子系统结构参数如表1所示。

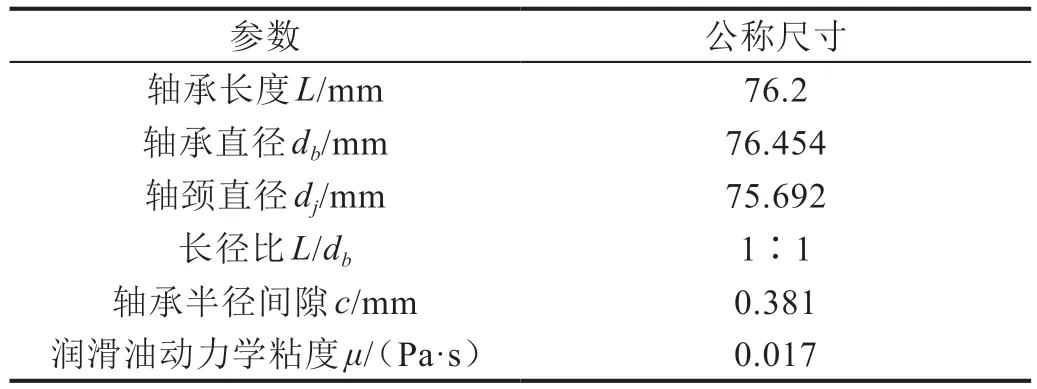
表1 滑动轴承转子系统结构参数表

圆度误差对油膜压力的影响规律如图8所示。当考虑圆度误差旋量dx﹥0时，滑动轴承油膜压力的最大位置在轴承宽度的中心，压力沿轴承长度均匀分布，并且其油膜压力分布与理想滑动轴承的油膜压力分布基本一致，但是旋量参数dx会改变最大油膜压力的数值。与理想圆截面相比，圆度误差旋量dx越大，油膜压力越大。

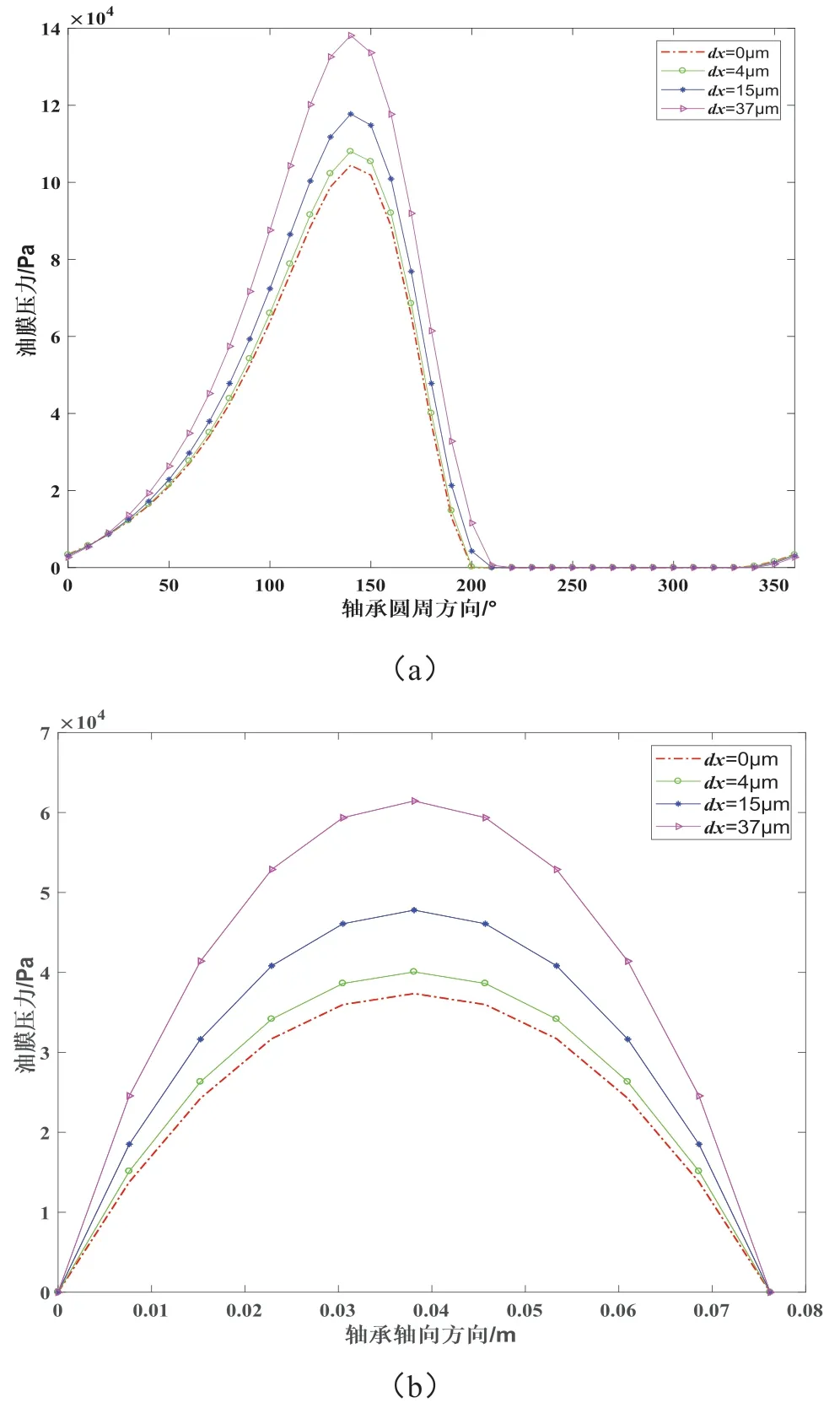
图8 圆度误差对油膜压力的影响

5 结语

1）本文在阐述滑动轴承油膜润滑理论研究现状的基础上，着重对求解Reynolds方程的三种边界条件进行了对比分析，发现传统的边界条件如半Sommerfeld边界条件、Sommerfeld边界条件不适用于对误差轴承进行润滑特性分析，而Swift-Stieber边界条件可以对误差轴承的润滑特性进行良好的分析。

2）在Swift-Stieber边界条件下求得的压力计算结果与实际情况较为接近，Swift-Stieber边界条件在数值计算中使用较多，是目前比较符合实际的边界条件。

3）通过算例求解了在Swift-Stieber边界条件下的Reynolds方程，并进一步研究发现，圆度误差旋量参数会改变最大油膜压力的数值，与理想圆截面相比，油膜压力会随着旋量参数的增大而增大。