一种可倾转四旋翼飞行器系统优化与控制研究*

廉欣芸 ，马 瑞 ，韩锦锦 ，冯辰宇 ，袁俊杰

（江苏理工学院机械工程学院，江苏 常州 213001）

0 引言

随着飞行器的创新和发展，多旋翼技术成为众多学者关注的研究热点。多旋翼飞行器由于具有机动灵活、可控性强、体积小等优点，大规模应用于日常生活中。但传统多旋翼飞行器是一个欠驱动、多变量、强耦合的复杂非线性系统，无法实现六自由度全向运动，这在很大程度上影响了无人机的灵活性，目前很难独立控制传统四旋翼无人机完成空中接触作业等高难度任务。

为了解决常规四旋翼的欠驱动问题，科研人员研究出一种可倾转飞行器，即飞行器的每个旋翼可绕垂直于臂的轴进行倾转，通过改变旋翼倾转角度来获得各方向的推力和力矩，从而增加系统可控变量输入，使无人机成为全驱动或过驱动系统。近年来，国外学者也对可倾转多旋翼无人机构型进行了大量研究，Kawasaki等[1]提出了倾转机架的四旋翼飞行器，将相邻的两个螺旋桨分别固定在两个倾转轴上，再由两个电机驱动螺旋桨进行倾转运动。与传统四旋翼无人机相比，可倾转四旋翼无人机具有起降快捷、姿态平稳、可悬停执行任务的优点，在进行空中接触性作业时应用更加常见。

随着人工智能的发展，智能控制技术也越来越多应用在控制系统设计中，如模糊控制、深度学习、人工神经网络等。可倾转飞行器与传统飞行器相同，具有强耦合性、不确定性和非线性等特征[2]。目前，飞行器的飞行控制设计与研究已取得大量成果，如PID控制[3]、自适应控制[4]等控制算法。滑模控制作为一种特殊的有限时间控制，其系统的收敛时间上界与初始值无关，因此受到许多学者的关注[5]。

基于以上对于飞行器控制系统的研究，本研究设计了一种RBF神经网络以及非奇异快速终端滑模控制器，滑模控制克服了系统的不确定性，增强了系统对干扰和未建模动态的鲁棒性，RBF神经网络有效降低了模糊增益，减小了滑模控制产生的抖振，通过自适应权重的调节保证了整个闭环系统的稳定性和收敛性。

1 结构设计及系统建模

1.1 结构设计

本研究所设计的可倾转四旋翼飞行器在传统四旋翼飞行器的基础上设计了可倾转机构，利用双轴舵机作为旋翼倾转的驱动器，在每个旋翼上增加了一个双轴舵机，两端分别与无刷电机与倾转基座固定连接，舵机驱动带动电机绕机臂旋转，同时带动与电机相连的旋翼倾转，实现旋翼的倾转。可倾转机构如图1所示。考虑到飞行时电机驱动倾转机构会对旋翼产生推力，为了使飞行器在可倾转机构的运作下获得稳定的姿态，需进一步控制飞行器的位置。各旋翼的倾转方向如图2所示。

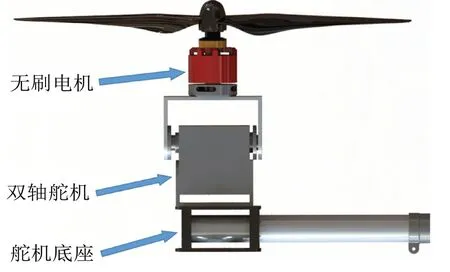
图1 可倾转机构

图2 旋翼倾转方向

1.2 系统运动学建模

定义地球固连坐标系Fg，机体坐标系Fb，在机臂轴线与旋翼轴线的交点建立四个子坐标系Fpi，原点位于机臂轴线xpi与旋翼轴线的交点，zpi与zb方向相同，坐标系定义如图3所示。

图3 坐标系定义

机体坐标系到地球固连坐标系的旋转矩阵为：

机臂坐标系原点在机体坐标系下的位置矢量为：

对于可倾转四旋翼飞行器而言，其刚体运动学模型与常规多旋翼飞行器相同，主要描述位置与速度、姿态角与角速率之间的关系。系统的运动学方程为：

1.3 刚体动力学建模

本研究设计的可倾转多旋翼的动力学模型可通过牛顿-欧拉方程得到[6]。对每个旋翼建立固定的旋翼坐标系，把旋翼推力和反扭矩投影到旋翼坐标系上，而且推力和反扭矩的数值成比例，所以由8个分力可以得到刚体的力和力矩。本研究中系统的平动方程在地球固连坐标系下描述，转动方程在机体坐标系下描述，可表示为：

其中，m为飞行器的质量，Jb为飞行器的惯性矩阵。Fg为飞行器在地球固连坐标系上受到的合外力，由自身重力Fg、四个旋翼对机体产生的合力Fp和未知的外部干扰力Fd组成。

其中，n是旋翼转速，k是旋翼升力系数，α是旋翼倾转角度。

Mb为固连坐标系下的合外力矩，由四个旋翼对机体产生的合力矩Mp和未知的外部干扰力矩Md组成。

其中，c是反扭矩系数。

1.4 控制分配

为得到合适的旋翼转速n和旋翼倾转角α，采用控制分配的方式将控制力和控制力矩分配到转速n和倾转角α上。由式（8）、式（9）空气动力对机身产生的合力/力矩与旋翼升力的分力呈线性关系[7]：

其中，A是常数矩阵：

执行机构中间动作量可以表示为：

控制分配矩阵是不含倾转角变量的常数矩阵。可直接获得真实控制量旋翼转速n和角度α。

2 基于神经网络的控制器设计

2.1 控制器结构

常规四旋翼由于其欠驱动性无法实现完整意义上的六自由度运动，需要单独设计位置与姿态控制器。而本研究的可倾转四旋翼是一种过驱动系统，可以实现六自由度独立运动，因而六自由度的控制器可独立设计[8]，此处将位置的三个自由度和姿态的三个自由度看作矩阵处理，分别设计位置控制器与姿态控制器。控制器结构如图4所示。

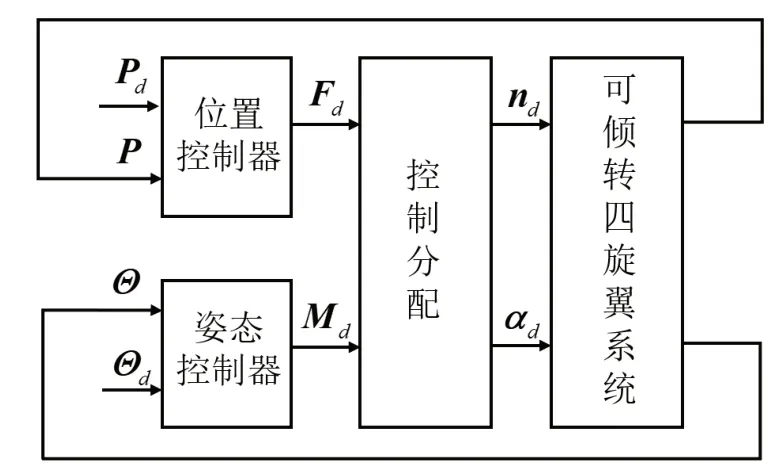
图4 控制器结构

2.2 控制器设计

以设计位置控制器为例，根据牛顿-欧拉方程推得无人机的平动动力学模型为：

假设期望跟踪参考位置为Pd，定义轨迹跟踪误差为ep=P-Pd，由此可得位置系统误差为：

定义非奇异快速终端滑模面[9]为：

对式（16）进行一阶求导：

在不考虑外部干扰的情况下设计等效控制律与切换控制律，式中令，Fd=0，可得：

式中，λ1﹥0，为使系统状态点能够到达滑模面，设计系统的控制律为：

RBF神经网络具有万能逼近特性[10]，其逼近位置模型算法为：

设计自适应律为：

将式（23）代入式（22），可得：

3 仿真测试分析

根据得出的控制律与可倾转四旋翼飞行器在MATLAB的Simulink环境下搭建系统模型并进行仿真测试分析。

物理参数如表1所示。

表1 动力学模型物理参数

假设期望轨迹跟踪的参考位置为：

偏航角期望值为ψd=π/3，四旋翼飞行器飞行过程中所受的干扰力与干扰力矩分别为：

根据上述仿真条件，对四旋翼位置与姿态进行仿真，其仿真结果如图5、图6、图7所示。由仿真结果可知，经过非奇异快速终端滑模控制的位姿在神经网络的逼近下达到与期望值快速逼近的效果，实现较好的轨迹跟踪和期望的响应特性。经过神经网络逼近的控制输入趋向平稳，有效控制了抖振，保持了系统的鲁棒性。

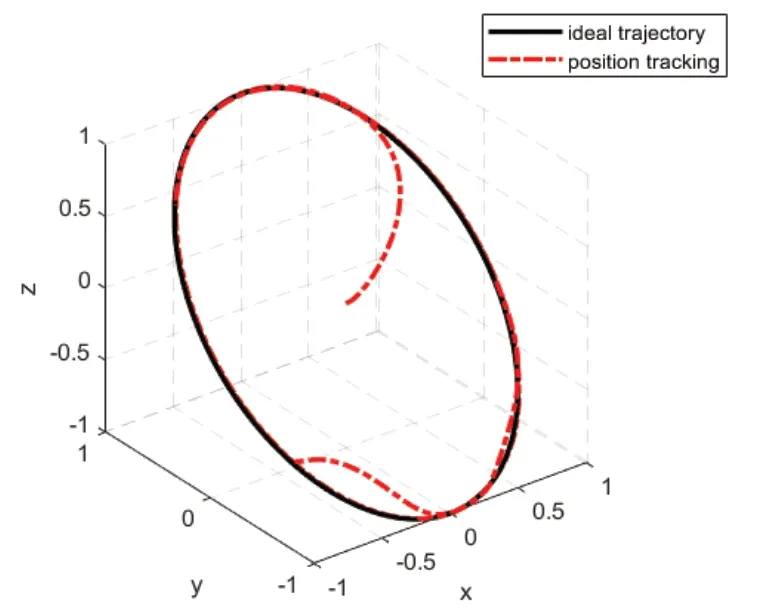
图5 位置跟踪三维效果

图6 x、y、z方向轨迹跟踪

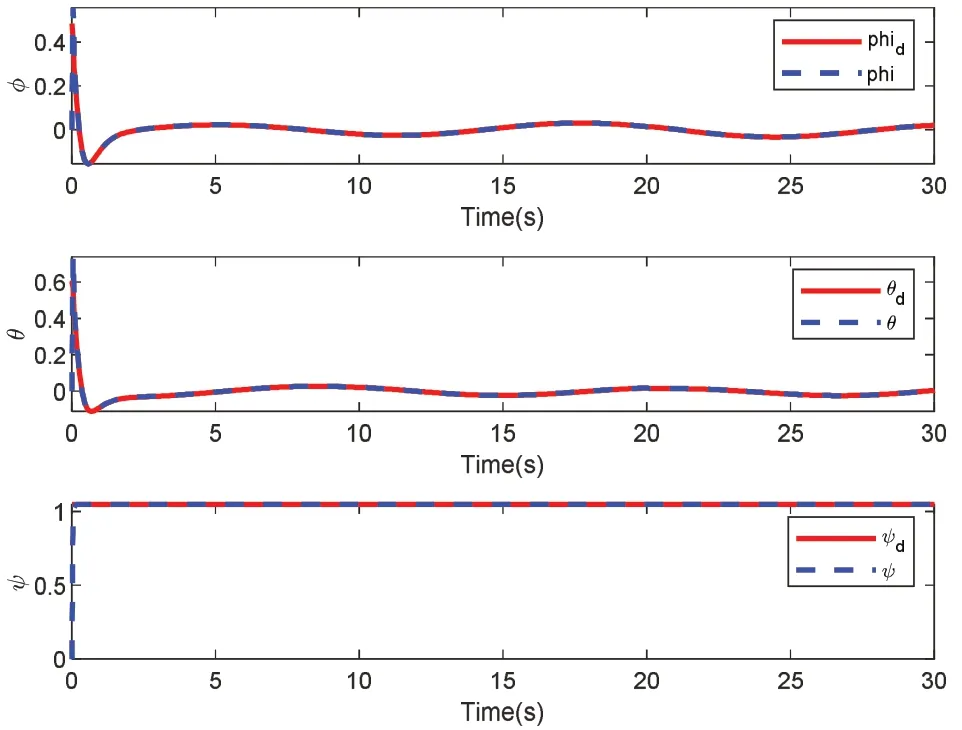
图7 ϕ、θ、ψ姿态角度跟踪

4 结论

本研究设计了一种可倾转四旋翼飞行器的构型。在传统四旋翼飞行器的基础上设计了可倾转结构，实现飞行器的全驱动；提出动态控制分配与位姿解耦控制方法，通过构造中间控制量对控制分配进行线性化处理。根据飞行器的位置与姿态的动力学模型单独设计控制器，采用RBF神经网络结合非奇异快速终端滑模控制可倾转飞行器的位置与姿态，结合等效控制律和切换控制律共同设计滑模控制，利用神经网络自适应控制逼近虚拟控制量，通过MATLAB/Simulink仿真验证了该控制器的可行性，该控制器能够在较快时间内实现轨迹跟踪，具有较强的稳定性与抗扰性。