界面极限滑移条件下的液膜密封流场平均速度分布规律*
2023-05-25曹志康黄茜茜陆雨佳
曹志康 胡 琼,2 卢 迪 肖 洋 陈 阳 王 衍 黄茜茜 陆雨佳
(1.江苏海洋大学机械工程学院 江苏连云港 222005;2.南京航空航天大学直升机传动技术重点实验室 江苏南京 210016)
现代工业的飞速发展要求密封设计向高工况、长寿命方向推进,而密封技术涉及多门学科交叉,其相关理论极为复杂。对于高速运转的密封装备而言,常会出现泄漏、振动、噪声等失效现象。相关研究显示[1],这可能是由液膜空化泡受扰引发流场大幅波动所致。因此,考虑空化效应的液膜密封微尺度流场速度分布规律研究仍然是先进密封技术领域的重点。然而,对于工程实际问题,人们关心的往往不是瞬时局部的微观变化量,而是整体平均压力、平均速度等一些宏观量,这些宏观量受流固界面黏性剪切应力的影响及流场平均速度与剪切应力的数学关系如何,目前在液膜密封技术领域研究中鲜有报道。
有研究[2-3]显示,高剪切率会导致流体内部由压应力转变为拉应力,当拉应力超过临界值后便会发生空化。范毓润教授团队研制了一种Couette流变仪,测得-0.045 MPa压力,约75 000/s剪切率下,淡水发生空化的临界切应力约为100 Pa,并指出黏度随剪切率升高无明显变化[4]。谢方伟教授团队研究发现离合器摩擦间隙流场中出现的气体是在剪切空化作用下,油液发生了从液体转换成油液蒸汽的相变[5],且转速越高,油膜空化程度越剧烈,气泡破碎加剧,并从槽区扩展到非槽区[6]。
BOCQUET和BARRAT[7]的研究表明,当液膜密封运行时,动环旋转、静环静止,使得密封微间隙内液膜与动环端面之间存在相对切向运动速度,从而产生边界滑移,而微/纳尺度下的边界滑移对系统性能影响较大,不容忽视。描述边界滑移问题的物理模型主要有2种:一种是滑移长度模型[8],另一种是极限应力模型[9]。滑移长度模型是由Navier在线性滑移边界条件假设上建立起来的,即滑移速度与局部剪切率成正比,该模型目前应用最广泛[10-11]。刚发生边界滑移时流体所受的临界拉应力,称为极限应力,根据极限应力大小判断边界滑移大小的方法,称为极限剪应力模型。吴承伟团队研究发现,极限剪应力模型比滑移长度模型优异的地方在于,极限剪应力模型可准确描述高剪切率流体流动的边界滑移[12]。
还值得关注的是,当两个表面具有不同极限剪切应力时,界面滑移只发生在极限剪应力较小的表面[13],并且即使某一个界面极限剪应力为0时,仍然有较大的流体承载力;当两个表面的极限剪应力互换时,流体承载力没有变化[14]。可见,无论液膜密封流体型槽底面是剪切应力最大(无边界滑移)还是无剪切应力(边界滑移最大),都可以维持完整液膜,可不考虑液膜收缩效应。
为探究流固界面黏性剪切应力的影响及流场平均速度与剪切应力的关系,本文作者对比研究液膜密封流体型槽与液膜界面无滑移和无剪切2种极限情况下的微流场平均速度分布规律,考察液膜密封槽区底面与液膜界面剪切应力对流场的作用效果,并基于极限切应力边界滑移理论,建立槽区界面剪应力-速度模型,以期为液膜密封高速失稳机制的阐释和抑制提供理论和方法参考。
1 几何模型
图1所示为螺旋槽液膜密封(简称S-FFS)端面几何结构示意图。图中,h0表示非槽区平均膜厚;hg表示螺旋槽轴向深度;α为螺旋线螺旋角。螺旋槽开设在静环端面上,螺旋线方程为

图1 S-FFS几何结构示意Fig.1 Schematic of S-FFS geometric structure
r=rgeθtanα
(1)
式中:θ为周向角度。
2 密封间隙Couette流动模型
Couette流动是指上下两平行平板所组成的间隙内充满黏性为μ的流体的不可压缩的恒定流动,上平板以速度U相对下平板运动,这与密封间隙的工作原理极为相似,因此液膜密封流体型槽内的流场流动在很大程度上可基于该模型进行描述。此外,现有研究广泛指出此类微尺度流体膜与壁面间存在边界滑移[15-16],用滑移速度us和滑移长度Ls描述,流动模型示意图如图2所示,其中两平板间距为H,且被密封水为牛顿流体、等密度、等黏度,流动恒定,不考虑体积力,则Navier-Stokes方程为

图2 考虑边界滑移的Couette流动模型示意(以线性分布为例)Fig.2 Schematic of Couette flow model considering boundary slip (taking linear distribution as an example)
(2)
(3)
(4)
由于:①两个方向的速度u和v相对于z的梯度较其他两个方向大;②流动为三维,在z方向没有变化;③当流速u达到临界流速uc时,下平板开始出现边界滑移,当u=U,且U>uc时,滑移速度为us;④压力在膜厚方向的梯度dp/dz≈0,因此,速度u和v的二阶偏微分方程可写为
(5)
(6)
边界条件为
(7)

(8)
(9)
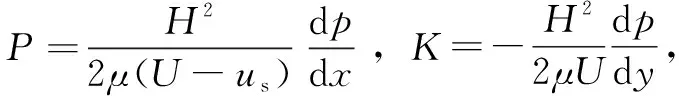
(10)
(11)
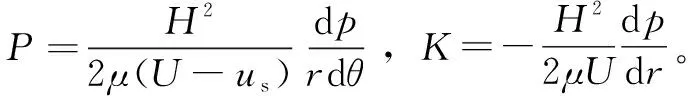

图3 S-FFS流体型槽内的Couette流动Fig.3 Couette flow in the S-FFS microchannel:(a)circumferential velocity distribution with different P;(b)radial velocity distribution with different K
3 液膜密封流场数值计算与结果分析
3.1 数值计算方法
文中采用文献[18]中的计算模型(称为BTF模型),即通过流动因子ξ来确定密封端面间流体的流动状态,具体计算方法按文献[19],其中径向平均线速度按下式计算[20]:
(12)
式中:ri、ro分别为密封面内侧和外侧半径;pin为内径侧入口压力;pout为外径侧出口压力;μ为动力黏度。
利用上述方法,将表1中的计算参数代入计算后得ζ=0.20<9/16为层流,与众多学者在开展相关研究时确定的流态一致[21-25],因此下文计算采用层流模型。

表1 几何参数与工况参数Table 1 Geometric and operating parameters
假设液相不可压缩、黏度不变,气相为理想气体,两相均匀混合,忽略流体重力和密封端面变形的影响,S-FFS密封环两端面保持平行,密封流体型槽内流体流动连续。由于微流场中存在液体低压气化,这是空化区形成的主要原因之一,故采用Mixture模型,液相为主相,气相为次相,而空化模型则选择计算精度较高的Schnerr-Sauer模型[26-27]。采用有限体积法求解两相流连续性方程、动量方程和能量方程。考虑S-FFS为周期对称结构,为缩短计算时间,选取1/Ng周期建立模型,周期对称面Γ1和Γ2为周期边界,外径侧为常温水介质入口,内径侧为大气出口。由于流体型槽开设在静环端面,所以液膜与静环贴合面为静止壁面,与动环贴合面为旋转壁面,其中在设置静止壁面时,针对槽区表面,通过剪切条件的选择实现其无滑移、无剪切2种极限状态。采用文献[28]中的网格划分方法,最终膜厚方向尺寸扩大1 000倍后的1/Ng周期网格模型与边界条件分别如图4(a)和(b)所示。使用压力-速度耦合算法,连续性方程用PRESTO!算法离散,动量方程和空化方程均采用较高精度的QUICK算法离散。考虑空化计算复杂性高,计算较难收敛,将松弛因子调为0.1~0.2,同时为收敛充分,将收敛精度尽可能调低,设为10-8可获得稳定结果。基于传统无滑移边界条件,采用上述方法与文献[29]中的实验结果进行对比,其参数为:G-24-5样件,外半径ro=0.032 m,内半径ri=0.024 m,槽数Ng=24,膜厚h0=7×10-6m,夹角Δθg=8.4°,槽深hg=4.6×10-6m,转速N=142 r/min,两侧压力po=pi=100 kPa,空化压力pc=30 kPa,动力黏度μ=0.083 Pa·s,承压力Fo=44.1 kN。文中计算结果与文献实验结果对比如图5所示,可见两者的空化区形状和面积大小较为一致,不过实验中槽区底面粗糙度对流场可能存在附加影响,使其空化区面积略小于文中理论计算结果。
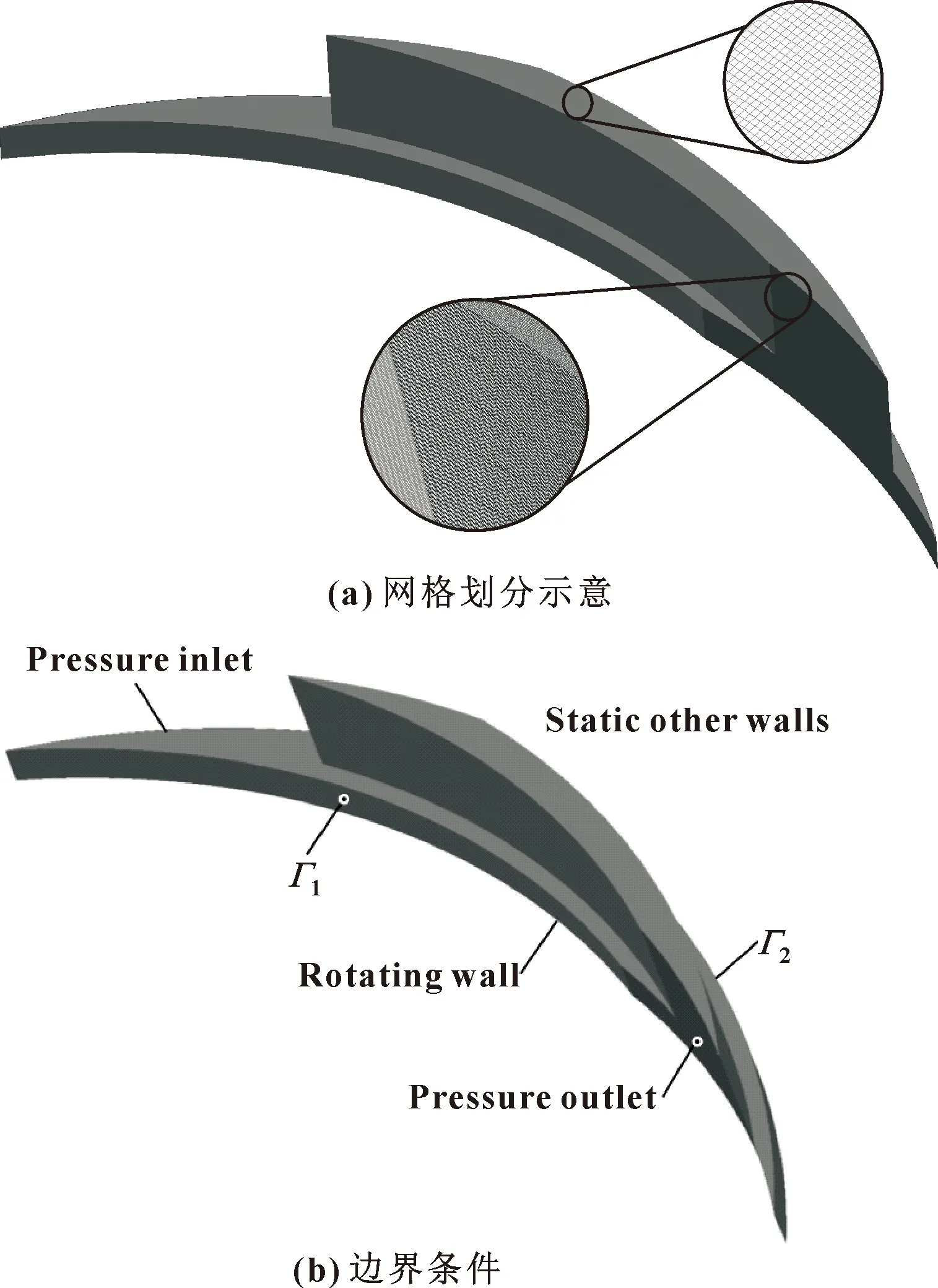
图4 网格划分示意及边界条件Fig.4 Schematic of grid division(a) and boundary conditions(b)
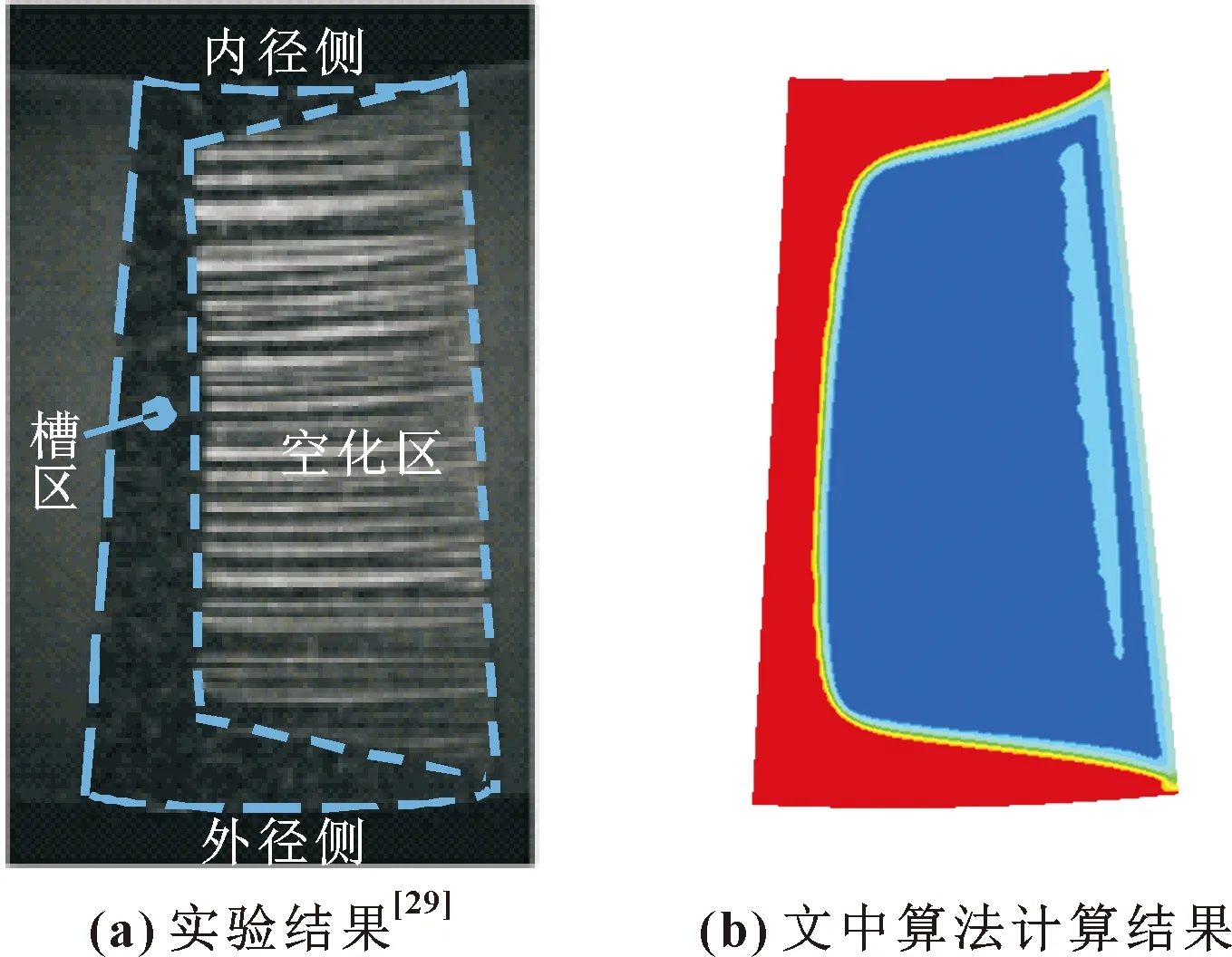
图5 文献实验结果与文中计算结果对比Fig.5 Comparison between the experimental result in the literature[29] (a)and the calculated result in this paper(b)
3.2 计算结果与分析
3.2.1 压力梯度分布规律
压力梯度数值大小和正负可以明确反映流场速度变化快慢和方向,因此考察不同转速时在无滑移条件和无剪切条件下距动环端面不同膜厚处x、y和z方向的压力梯度,结果如图6和7所示。

图6 不同转速时无滑移条件下的压力梯度分布Fig.6 Average pressure gradient distribution with no slip under different rotational speeds:(a)pressure gradient dp/dx; (b)pressure gradient dp/dy;(c)pressure gradient dp/dz
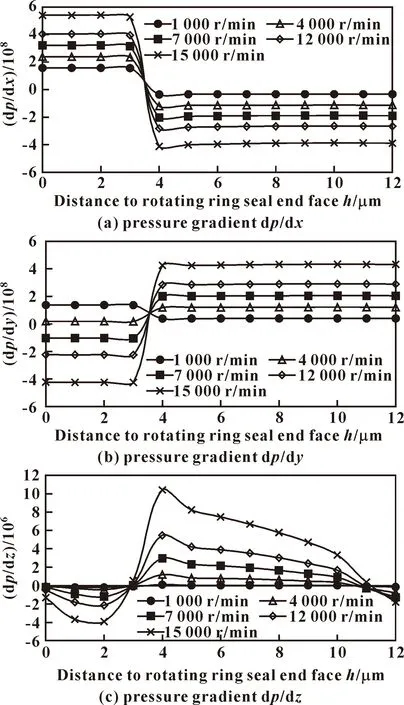
图7 不同转速时无剪切条件下的平均压力梯度分布Fig.7 Average pressure gradient distribution with no shear under different rotational speeds:(a)pressure gradientd dp/dx; (b)pressure gradient dp/dy;(c)pressure gradient dp/dz
图6显示,在边界无滑移的条件下,x、y方向上的压力梯度在槽区近槽台处方向发生逆转,但在h=3~4 μm处的逆转区间以外,两方向的压力梯度均保持为常数;z方向上的压力梯度在膜厚方向的变化规律相对复杂,在非槽区压力梯度为负值,在槽区为正值,整体规律为减小-增大-减小,在4 μm处出现最大值,在接近槽底面处出现稍许反升;整体而言,转速越高,各方向压力梯度数值越大(不考虑方向),z方向的压力梯度远小于x和y方向。与无滑移条件相比,图7所示无剪切条件下的各方向压力梯度均较大,在z方向上,近槽底面处的压力梯度值持续下降而没有出现反升,其他规律两者则基本一致。综上所述,当单独考察非槽区和槽区流动时,平均压力梯度dp/dx和dp/dy为常数,dp/dz可忽略不计,即非槽区和槽区仍可视为Couette流动,与文中第2节理论模型相对应;而槽区台阶对流场的影响,应做特殊考虑,尤其当考察密封稳定性时,轴向压力波动不可忽视。
3.2.2 流体型槽速度分布规律及拟合
受旋转速度、径向压差、流体型槽、液体黏性、壁面材料特性等的影响,微间隙内的流场极为复杂,探索流体型槽速度分布规律对建立速度场模型至关重要。因此,文中沿膜厚方向考察在不同滑移边界及不同转速条件下,膜厚分别为0~12 μm(其中,膜厚为0表示动环端面,膜厚为12 μm表示静环流体型槽底面)处液膜截面各方向(轴向(膜厚方向)、径向和周向,以及合成方向)的平均速度分布规律,结果如图8和9所示。
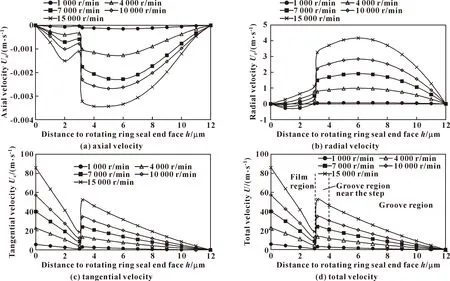
图8 不同转速时无滑移条件下流体型槽流场平均速度分布规律Fig.8 Average velocity distribution of microchannel flow field under no slip condition at different rotational speeds:(a)axial velocity;(b)radial velocity;(c)tangential velocity;(d)total velocity

图9 不同转速时无剪切条件下流体型槽流场平均速度分布规律Fig.9 Average velocity distribution of microchannel flow field under no shear condition at different rotational speeds:(a)axial velocity;(b)radial velocity;(c)tangential velocity;(d)total velocity
从图8和9可以看出,2种极限条件下的速度分布规律主要的区别有两处:①无滑移条件下流场与密封环表面间不存在速度滑移,而无剪切条件下的槽底面存在显著的速度滑移,且随转速上升而增大;②无剪切条件下的轴向和径向平均速度较无滑移条件时大,但切向速度和合成速度差距很小。图8(a)和图9(a)显示,2种条件下,轴向平均速度均从开槽端面指向未开槽端面,非槽区最大速度发生在h=2 μm处,槽区内部的轴向速度大于非槽区,并受转速影响更大,即转速上升时,槽区速度的增加幅度大于非槽区,且最大速度发生位置逐渐向台阶靠近。图8(b)和图9(b)显示,在不高于7 000 r/min时,非槽区的径向平均速度存在负值,说明有泄漏发生,但随转速上升速度增大,负值消失,但无滑移边界条件下的最大径向平均速度位于槽区h=6 μm处,而无剪切条件下位于h=12 μm处(槽底面)。图8(c)和图9(c)显示,液膜的切向(即周向)平均速度占主导地位,其值远大于轴向和径向平均速度,且转速越高,主导地位越突出,且在非槽区,切向速度沿轴向(从动环端面到静环端面)近乎呈线性减小,但在槽内台阶处(h=3 μm)出现速度阶跃,随后近似呈抛物线规律下降。图8(d)和图9(d)显示,液膜三维合成平均速度分布规律与切向平均速度基本一致,说明较高转速下液膜密封的合成速度分布规律由切向速度决定,且非槽区可近似为简单Couette流动(即图3中的P=0),槽区可认为是逆压梯度Couette流动(即图3中的P<0)。由此可见,由于液膜的径向速度和轴向速度远小于切向速度,在一般压差下(文中为2 MPa),可忽略径向和轴向速度对流态的影响,而流体型槽的存在几乎不影响非槽区流场,这与ARNDT等[30]所提出的“孤立型不平整表面对流场只产生局部扰动,对整体边界层影响较小”观点相符。
4 流体型槽界面剪切应力-速度拟合模型
鉴于3.1和3.2节的分析结果,可尝试基于Couette流动理论建立S-FFS流体型槽界面剪切应力模型。如果按无滑移边界下的简单Couette流动理论,剪切应力可近似表示为
(13)
式中:u为流体型槽内任意膜厚处的切向速度,m/s;U为动环端面周向的平均线速度,m/s;H为考虑非槽区和槽区的综合膜厚,H=h0+hg=1.2 μm。
通过计算,其结果与数值仿真偏差很大(如图10所示),这是因为流体型槽的存在改变了流体型槽流场分布,不能再以简单Couette流动理论描述。
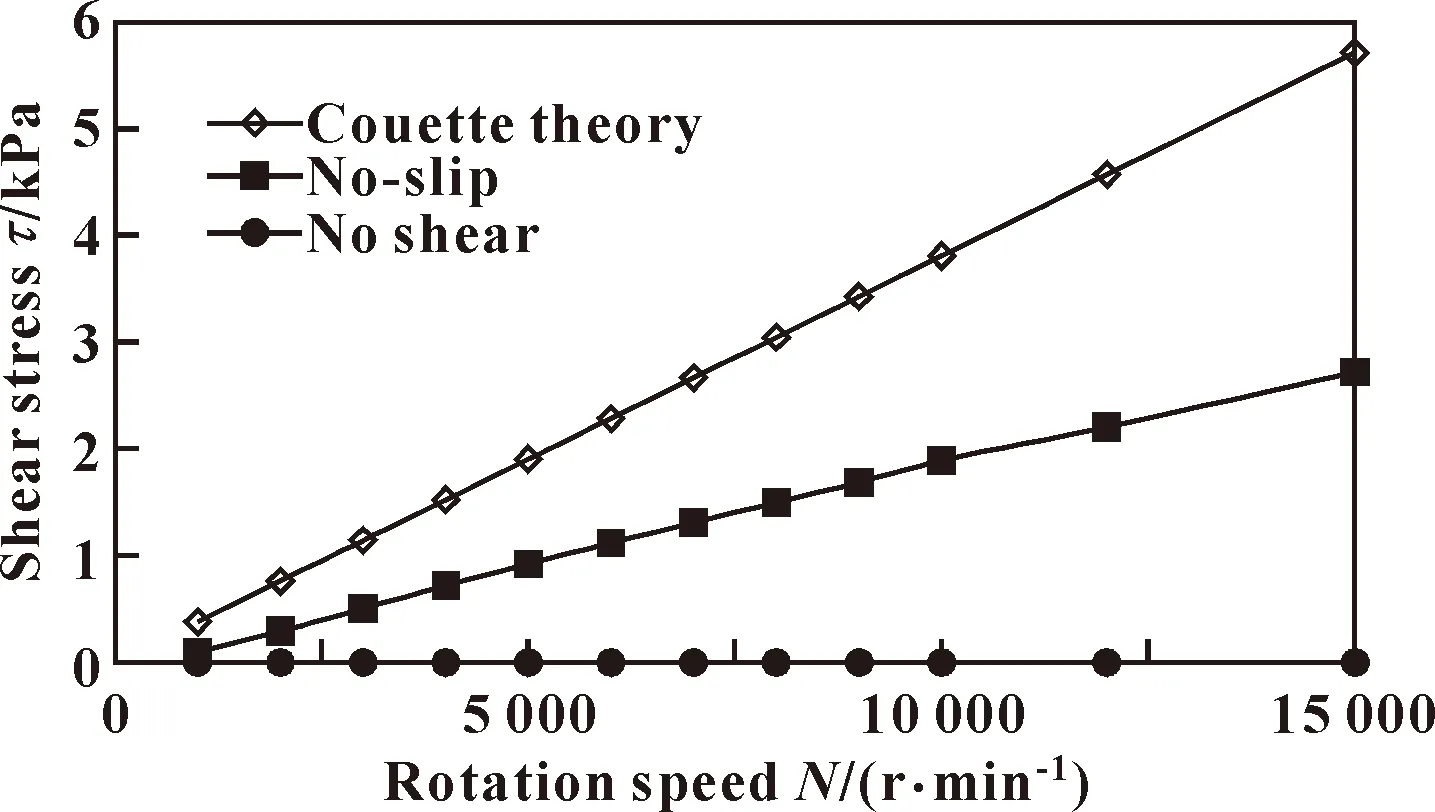
图10 流体型槽界面剪切应力与转速的关系Fig.10 Relationship between shear stress of microchannel interface and rotational speed
在流体型槽中,液体的黏度由两部分组成,一部分是液体的常规黏度,另一部分是由固壁和液体分子相互作用导致的附加黏度。因此,流体型槽中的黏性系数可以表示为
μ=μ0+φ/yn
(14)
式中:φ/yn是附加黏度,φ依赖于材料特性,y是到固壁的距离。
当y趋向于0即在亲水壁面上时,黏度为无穷大,即液体分子黏附于固壁表面而不移动,这对应上述无滑移条件;当到固壁的距离超过一定值时,液体的黏性趋向于常数μ0;或是当固壁为疏水材料时,附加黏度很小,此时液体的黏性同样趋向于常数μ0。
当液膜与密封环界面的剪应力达到极限值,液体将沿固壁表面发生滑移。由于受到周向线速度、径向压差、液体黏度及流体型槽参数等的影响,流体型槽内液体沿槽型方向流动,结合第3节的分析结果,绘制如图11所示的S-FFS液膜流动速度示意图,其中,上表面为亲水动环端面,下表面为疏水静环流体型槽底面。根据上述黏度特性,当流体速度u=uc时,下表面刚好发生滑移,此时的临界切应力

图11 液膜密封流体型槽界面速度滑移示意Fig.11 Schematic of interfacial velocity slip of liquid film seal microchannel
τlim=(μuc)/h
(15)
下表面滑移速度为us。
根据3.2节的速度分析结果,对流体型槽底面无滑移和无剪切2种极限情况下的液膜速度进行拟合,拟合结果如图12—15所示。
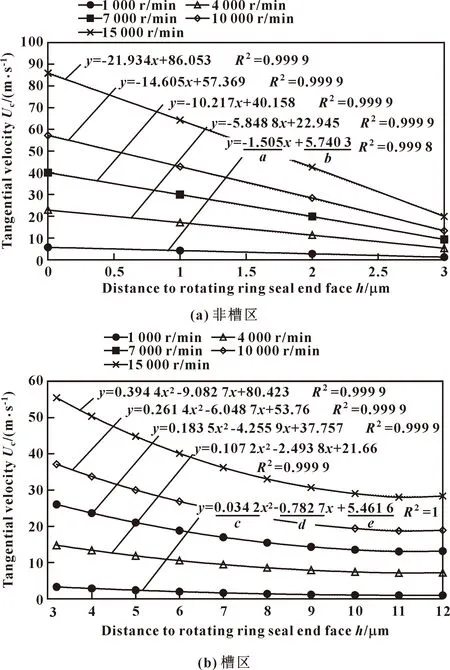
图14 不同转速下无剪切液膜合成平均速度拟合Fig.14 Fitting of total velocity of no-shear liquid film at different speeds:(a)non-groove region;(b)groove region
图12和13中的自变量x表示膜厚(以下用h表示),图14和15中的x表示转速(以下用N表示),据此可获得不同膜厚处的节点在不同转速下的平均速度:
①无滑移条件下
(16)
(17)
②无剪切条件下
(18)

(19)
对于无滑移时的槽区表面剪切应力(也为某转速下,开始滑移时的极限应力,即τN,lim)则可直接根据槽区流场速度规律计算,即
0.063 7)]×106
上式与数值计算对比结果如图16所示。结果显示:10 000 r/min以下时,两者偏差较小,在5%以内,而造成这些偏差的原因应该是文中研究所取速度为沿轴向不同膜厚处流场横截面的平均速度,实际上整个截面在径向和周向均存在一定的速度梯度。在高转速下,由于空化效应影响增强,槽区流场受扰程度增大,流动变得更加复杂,因此,平均流速规律曲线波动较大,难以通过常规曲线精确拟合,造成偏差较大。该问题可望在掌握流体型槽底面空化面积占比与转速确定性关系的基础上进行拟合,理由是:水蒸气的黏度小于水,所以流-固界面气体的存在会降低界面黏性剪切力,且气体面积越大,剪切力越小,而气层厚度与剪应力大小无关[31]。
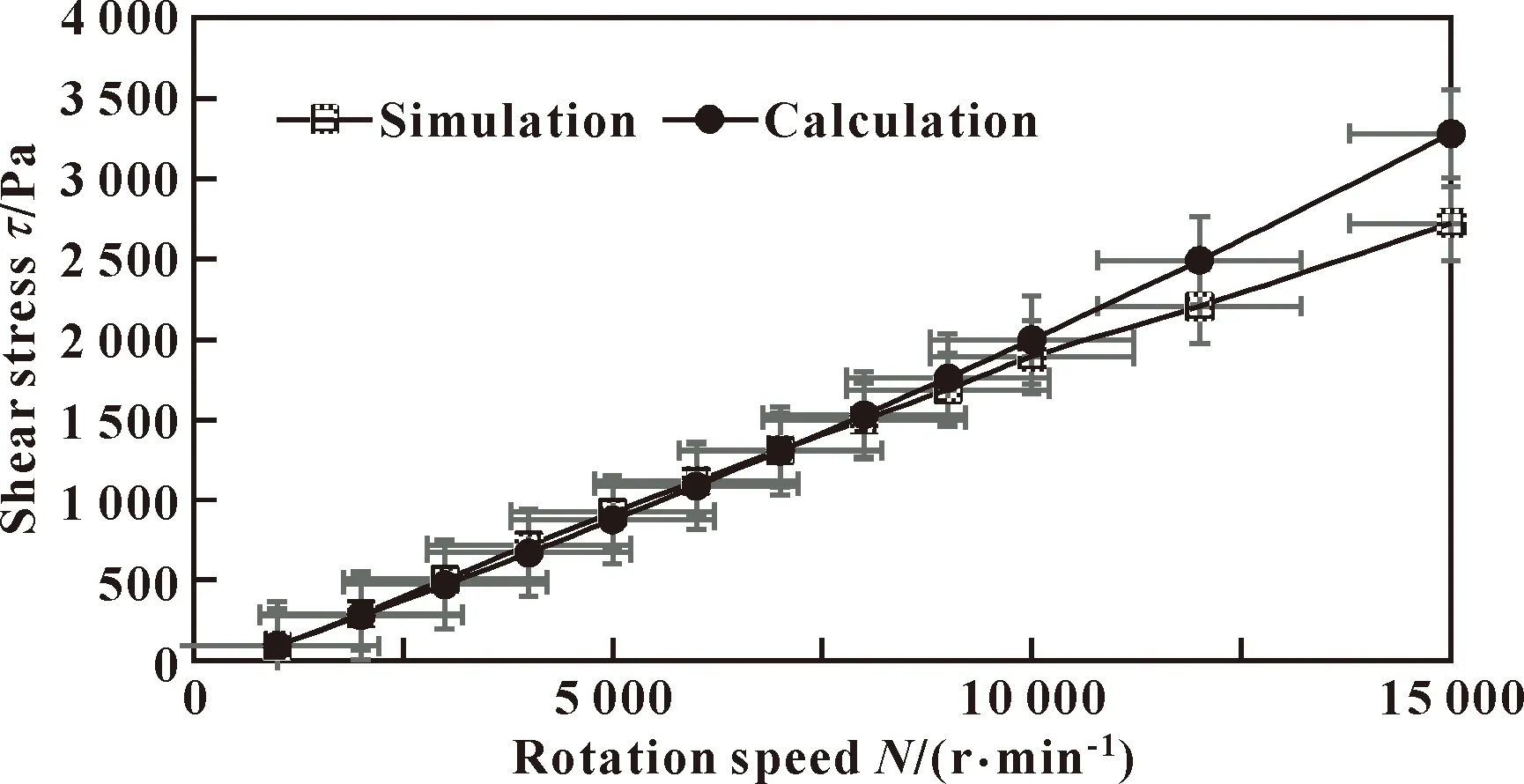
图16 拟合计算与仿真对比Fig.16 Comparison between fitting calculation and simulation
5 结论
(1)两种极限条件下,液膜密封微流场平均压力梯度在轴向距非开槽端面3~4 μm处(近台阶槽区内部)发生突变,非槽区(h=0~3 μm)和槽区(h=4~12 μm)的平均压力梯度dp/dx和dp/dy为常数,但轴向压力梯度dp/dz波动较大,当考察密封稳定性时,轴向压力波动不可忽视。
(2)液膜的切向平均速度远大于径向和轴向平均速度,决定三维合成速度分布规律;非槽区和槽区流动相对独立,非槽区流场可视为简单Couette流动,槽区视为逆压梯度Couette流动,各方向速度均随转速上升而增大;轴向平均速度从开槽端面指向未开槽端面,非槽区最大速度发生在h=2 μm处,槽区内部轴向速度大于非槽区,转速上升,速度增幅更大,且最大速度发生位置向台阶靠近;在不高于7 000 r/min时,非槽区存在指向泄漏方向的径向平均速度,但随转速上升而消失,无滑移条件下的槽区最大径向平均速度位于h=6 μm处,无剪切条件下位于槽底面。
(3)在槽底面无剪切条件下,槽底流-固界面存在较大的径向和切向速度滑移,且转速越高,滑移速度越大;流体型槽界面剪切力-速度拟合模型与仿真结果在转速不高于10 000 r/min时,偏差在5%以内,但在高转速时,空化效应增强,需对剪切应力-速度拟合模型进行修正。
