立足新课标，发展学生深度思维的教学思考

2023-05-25江苏省无锡市江阴市城西中心小学

小学教学研究 2023年15期

江苏省无锡市江阴市城西中心小学金雯

《义务教育数学课程标准（2022 年版）》指出，教师需要留给学生足够的时间和空间，让学生经历观看、试验、推测、运算、验证等活动过程。教师是教学活动的组织者和引导者，需要关注学生发展，将学生作为学习主体，遵循深度思维的培养原则，实现“教”与“学”的统一，逐渐发展学生的深度思维。

一、遵循深度思维培养原则，开展主体教学

（一）主体性原则

小学生好奇心强，是教学活动的主体。因此，教师在培养学生的深度思维时，需要尊重学生的认知特点和发展规律，遵循主体性原则，因势利导，让学生在丰富自身数学知识的过程中发展思维能力。

（二）渗透性原则

深度思维的培养并非单纯的教育行为，而是渗透于教学活动的全过程，教师需要遵循渗透性原则，将深度思维培养融入学生的观察、类比、实践活动中，让学生积累数学表象信息，思考和领悟数学规律，进而让深度数学思维的发展水到渠成。

（三）启发性原则

深度思维是学生需要形成的学习品质，是学生对外界输入信息主动加工、处理的最终结果，教师需要掌握深度思维形成条件，对学生思维加以有效引导，才能将学生思考问题的路径逐层引向更深层次，让学生思维向深度和广度发展。因此，教师在培养学生深度思维时需要遵循启发性原则。

二、优化数学教学策略，培养深度思维

（一）引导学生观察，奠定培养基础

1.激发学生浓厚的观察兴趣

教师可以根据学生的天性采用多样化的方法，激发他们观察、探索和求知的欲望。

例如，在教学“图形的运动”一课时，教师可以采用“游戏激趣”的方式，为学生准备传统的益智玩具——七巧板，引导学生观察七巧板中的三角形、正方形和平行四边形板块特点，利用这些板块自由拼接成各种动植物、人物和建筑物的形象，让学生在“游戏”过程中观察、交流、操作，加深对图形变换特点和方法的理解认知。

教师在培养学生观察兴趣时，要“重视直观” “重视学生直接体会”，在教学中力求贴近学生的实际生活，符合学生的认知规律，体现教学方法的多样性，使学生在数学活动中有耳目一新的感觉，从而提升其观察兴趣的培养效果。

2.培养学生良好的观察品质

学生观察品质的形成需要经过“观察—思考—实践”，这样才能将事物的表象信息内化为自身具备的思维知觉，进而形成数学素养。教师在培养学生的“观察品质”时，要强调观察的目的性和全面性。例如，在“游戏激趣”的观察活动中，教师可以引导学生观察七巧板的成型作品，让他们思考作品是由哪些图形构成的，接着引导他们动手操作，让他们在实践中加以体会。这样，学生在无意识中经历了“信息获取—信息加工—信息运用”的过程，他们的观察活动更加全面、更加完整，久而久之，学生的观察能力将会获得大幅度提升。

（二）鼓励大胆猜测，发展类比思维

类比指的是观察两种不同事物的外在表象，找出两者之间的相似之处，判断两者可能存在的共性，然后进行由此及他的“猜测”，得出最后的数学结论。在培养学生的深度思维时，教师可以在引导学生观察的基础上，鼓励学生大胆猜测，发展他们的类比思维。例如，在教学“圆的面积”时，教师可以先引导学生复习旧知，让学生回顾平行四边形、三角形、梯形等图形的面积计算公式的推导过程：都是在面积不变的情况下转化成以前学过的图形，再根据转化前后两个图形的关系，推导得出新学图形的面积计算公式。接着，教师可以引导学生大胆猜想圆是否也能转化为已学过的图形来计算，在学生“猜想”后，实践操作，将圆平均分成若干等份后再拼接起来，让学生观察拼接后的图形。此时，学生会发现，拼接成的图形近似于一个长方形。教师进一步引导学生大胆猜测圆的面积与长方形面积之间的关系并深入思考，得出结论：如果圆分的等份越多，拼接后图形的边越接近直线，当等分数量无限多时，拼接的图形就是一个长方形。通过实践操作，学生不难发现，圆的半径r等于长方形的宽h，圆周长的一半等于长方形的长，再根据长方形面积计算公式，可以推导出圆的面积公式。

波利亚曾指出，在证明数学概念和定理前，需要经历猜想的过程，在猜想和类比中得出概念或定理的主导思想。猜想是创造性思考的基础，而类比则是将旧知与新知建立联系，引发进一步推理和论证。可见，教师在发展学生深度思维时，需要鼓励学生大胆猜测、大胆想象，让学生在类比的过程中形成解决数学问题的思路，从而促进学生“类比思维”的发展。

（三）开展数学实践，开发推理思维

《义务教育数学课程标准（2022 年版）》明确指出，学生除了接受学习外，动手实践也是学习数学的重要方式。数学的本质是对生活各事物的抽象，它源于生活又运用于生活，“百听不如一练”，要培养学生的深度思维，教师需要摒弃灌输式的教学方式，适当放手，开展实践，让学生在实操中发现问题，体验过程，深入思考，进而从某个或某些已知的判断中推想出新的结论，在强化思维的跳跃性的同时，逐步形成数学的推理思维。例如，在教学“三角形的内角和”一课时，教师可以利用问题创设思考情境：（1）什么是三角形的内角？（2）三角形有几个内角？（3）不同三角形，内角和一样吗？在问题的引导下，学生对“内角和”这个数学问题产生了兴趣。在此基础上，教师引导学生算出三角尺三个角度数的总和，得出“三角尺的内角和为180°”。接下来，教师抛出关键性问题：“其他三角形的内角和是多少呢？”将学生的思维从“三角尺”引向“普遍三角形”，让学生带着问题，进行数学探索实践。学生利用方格纸折、剪、撕等，制作出各种三角形，然后用量角器测量不同三角形内角的度数，通过将实测数据相加，得出“三角形内角和为180°”的结论。在本次教学中，教师利用创设问题情境的方式激发学生实践动机，利用问题引导，让学生从“个别现象”到“一般现象”探索，学生在实践活动中根据“一般现象”得出推理结论，从而推理思维得到锻炼，增加了数学思维的深度。

（四）教学内容拓展，锻炼归纳思维

归纳思维的培养通常经历“积累信息—信息处理—概括抽象”的过程，教师可以在习题教学中进行适当拓展，锻炼学生的归纳思维。例如，在练习教学中，教师给出下列一组数字（见图1），要求学生在图形的空白处填写适当的数。

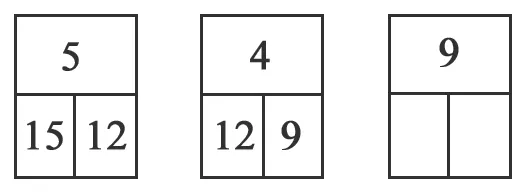
图1

学生在分析这道题时，需要从前两组数字中积累表象信息，然后处理信息，从中找出数的规律，从“个别”现象推出“一般性”结论。从第一组数字中可以看出5×3=15，15-3=12；而第二组数字中4×3=12，12-3=9，通过推理，可以得出第三组数字中9×3=27,27-3=24。因此，第三组数字中空白处应分别填写27 和24。教师在习题教学中引入拓展性内容，不但能够激发学生的挑战心理，还有助于学生展开从“个别”到“一般”的思考，进而发展学生的归纳思维。