一种蒸发波导预测的改进模型
2023-05-25王方方崔鸣宇
张 瑜,任 朔,王方方,崔鸣宇
(河南师范大学电子与电气工程学院,河南新乡 453007)
0 引 言
低空或超低空目标的探测是现代战争的有效手段之一。由于受地球凸起的影响,地海面上的雷达系统探测低空和超低空目标时的作用距离较小,一般为十几公里范围[1-2]。为了扩大雷达的作用范围,超视距探测成为目前雷达系统的主要方式。实现超视距探测功能的雷达系统主要有高频天波超视距雷达、高频地波超视距雷达和基于大气波导的微波超视距雷达三种类型。高频天波超视距雷达是利用高频无线电波经电离层的反射来实现,高频地波超视距雷达主要是利用高频无线电波地海面的绕射来实现,基于大气波导的微波超视距雷达是利用大气波导效应来实现[2-5]。由于高频天波超视距雷达和高频地波超视距雷达需要的设备复杂、造价高,需要部署的场地大,因此一般常用于在地面部署,无法在舰船上使用。基于大气波导的微波超视距雷达只是需要得到大气波导的特征参数就可以实现,具有造价很低、部署场地很小的优点,因此是舰船雷达系统实现超视距探测的首选方式。当然,这种超视距探测方式也常用于岸基雷达系统。
大气波导是一种特殊的大气层结,取决于大气修正折射率梯度。由于地海面上空的大气呈现不均匀分布,每层大气都有不同的大气修正折射率,当大气修正折射率的梯度小于0时就会形成特殊的大气层结,称为大气波导。当雷达的无线电波在大气波导内传播时,由于受到大气波导的陷获,使得无线电波只能在大气波导内传播,类似在一个金属波导管中的传播。这种方式的无线电波具有衰减小的特点,其传播距离很远,一般可达几百公里。大气波导主要分为悬空波导、表面波导和蒸发波导三种类型[3]。主要发生在陆地上空的悬空波导和表面波导出现的概率很小,出现在海面和海陆交界上空的蒸发波导出现的概率很大,因此利用蒸发波导更具有实用价值[6],这也是目前蒸发波导及其应用研究最多的原因所在。鉴于大气波导的出现概率和实用环境,在舰船和岸基上雷达系统实现超视距探测大都选用基于蒸发波导的微波超视距雷达方式。
要实现基于蒸发波导的超视距雷达探测,首先需要建立在蒸发波导内的大气修正折射率剖面模型(称为蒸发波导预测模型),预测模型的精度决定超视距雷达探测精度。大气修正折射率剖面主要通过两类方法获得,一是利用高精度的微波折射率仪进行移动测量[7-8],二是利用预报、预测等其他方法获得蒸发波导特征参数,再根据特征参数利用常用预测模型建立大气修正折射率剖面[9-13]。第一类方法由于受条件和使用场地的限制,作为检验大气修正折射率剖面模型的精度是很好的,但是不太适合岸基和舰船的实际应用。目前获得蒸发波导特征参数的方法较多,也具有一定的精度,但是常用的蒸发波导预测模型精度不太高。为了进一步提高蒸发波导预测模型精度,本文通过分析常用蒸发波导预测模型,建立了改进模型,使得其精度进一步得到提高,进而可进一步提高雷达超视距探测精度。
1 蒸发波导特征参数与常用蒸发波导预测模型
1.1 蒸发波导及其特征参数
海面水体由于受太阳照射使得水分蒸发,经与近海面大气的相互作用使得大气湿度快速下降,进而使得垂直大气的修正折射率快速下降,这种机理形成的大气波导称为蒸发波导。蒸发波导具有发生概率高、持续时间长、稳定性好、水平方向延伸大等特点,垂直高度一般都在距离海面40 m 以内[3,14]。
依据气象学理论和电波传播理论,当大气修正折射率M梯度dM/dh小于0 时会形成蒸发波导[1,3],即
式中:h为距离海平面的垂直高度,m;M为h高度处的大气修正折射率。
蒸发波导的高度形态如图1所示。蒸发波导的海面大气修正折射率M0可以由地面气象参数或其他方法直接得到。蒸发波导的特征量主要有两个,即波导高度ht和波导强度△M。波导高度ht是指大气修正折射率梯度dM/dh随高度从小于0 变化到大于0的结点离海面的高度,即大气修正折射率M从海面开始随高度减小,直到这一高度才开始增大的结点高度,它对应的修正折射率为Mt。波导强度△M是指波导层中大气修正折射率最大值与最小值之差,即△M=M0-Mt。
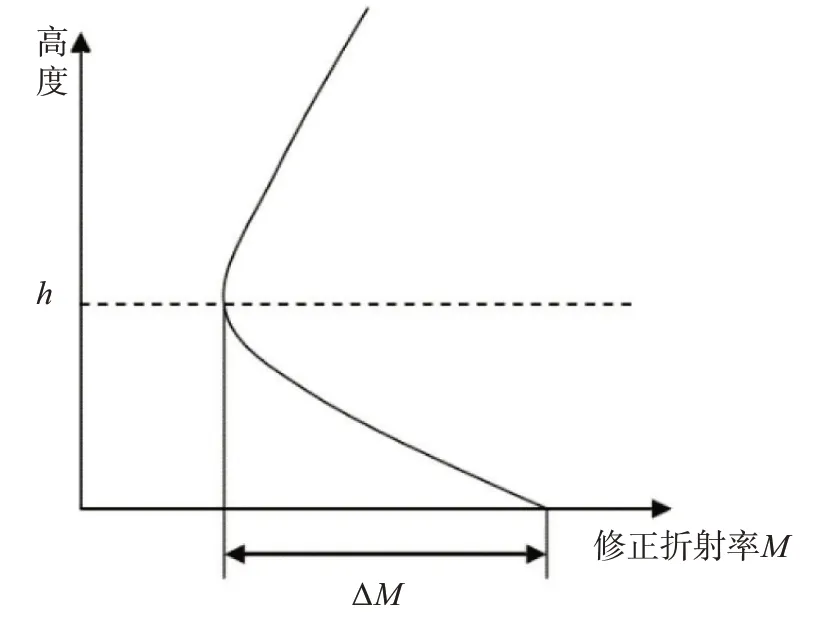
图1 蒸发波导及其特征参量示意图
1.2 常用蒸发波导预测模型
目前常用的蒸发波导预测模型主要是单参数模型[6,15],即
式中:M(0)=M0,为海平面的大气修正折射率;ht为波导高度,m;z0为空气动力学粗糙度因子,通常取z0=1.5×10-4,m。
2 常用蒸发波导预测模型的缺陷分析与改进模型的建立
2.1 大气修正折射率剖面模型的缺陷分析
从式(1)可见,在常用蒸发波导预测模型中,如果要得到大气修正折射率剖面M(h),只需要获得蒸发波导的波导高度ht和海平面的大气修正折射率M(0)=M0即可。海平面的大气修正折射率M(0)很容易根据实际测量得到,而波导高度ht可以通过各种预测方法获得。
当蒸发波导的波导高度ht和海平面的大气修正折射率M(0)确定后,蒸发波导内的大气修正折射率剖面就是一个确定的对数曲线。在实际蒸发波导测量中,发现许多蒸发波导具有相同的波导高度ht和海平面的大气修正折射率M(0),但是其波导强度不同,如图2所示。图2中,M1(h)、M2(h)为实际大气修正折射率剖面,Mt(h)为预测模型得到的大气修正折射率剖面。实际波导强度为△Mi=M0-Mi,i=1,2,…,由预测模型得到的波导强度为△Mt=M0-Mt,Mt可由式(2)计算得到。
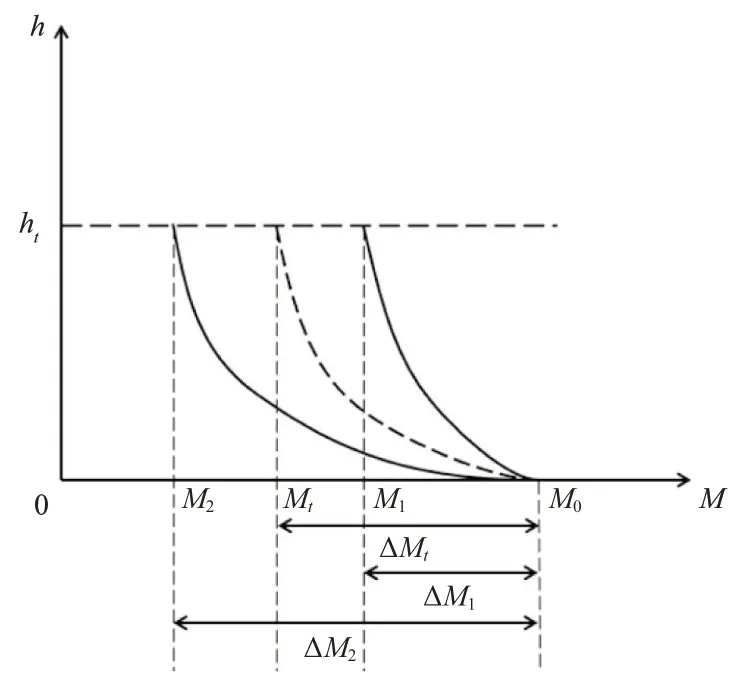
图2 实际蒸发波导剖面与预测剖面示意图
可见,在这些情形下,利用蒸发波导预测模型无法得到较为精确的大气修正折射率剖面,且实际波导强度△Mi偏离预测波导强度△Mt越大,则误差越大,进而影响雷达超视距探测误差越大。
利用蒸发波导模型(式(2))获得的大气修正折射率剖面的误差是没有考虑波导强度△M的影响,因此要想使得蒸发波导预测模型的计算结果更接近实际情况,需要对预测模型进行改进,加入波导强度的影响因素。
2.2 蒸发波导预测改进模型的建立
为了保持原有蒸发波导预测模型的原貌,改进后的预测模型是在原有预测模型的基础上增加波导强度ΔM的影响因子f(ΔM,h),即改进预测模型形式为
假设海平面的大气修正折射率为M(0)=M0,波导高度为ht,m;波导强度为ΔM。取h=ht,利用式(2)可计算得到波导高度ht对应的预测大气修正折射率Mt和预测波导强度ΔMt=M0-Mt。利用波导强度的定义可得到波导高度ht对应的实际大气修正折射率M=M0-ΔM,如图3所示。
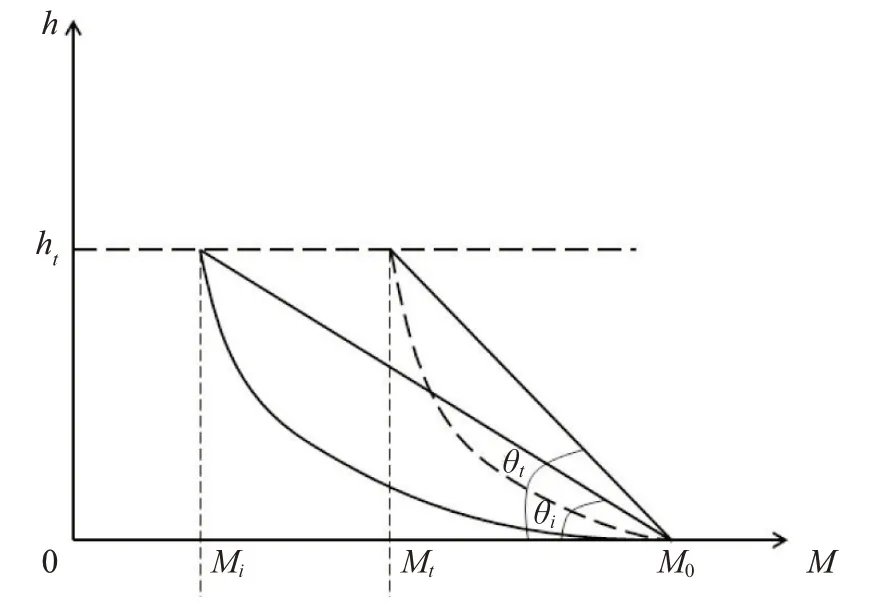
图3 蒸发波导预测改进模型
采用以M0为中心的线性旋转方式使得波导高度ht对应的预测大气修正折射率Mt等于实际大气修正折射率M。这样,波导强度ΔM的影响因子f(ΔM)为
由于
将式(5)代入式(4)可以得到
将式(6)代入式(3)可以得到蒸发波导预测的改进模型为
式中,Mt=M(0)+0.125ht
3 实验与分析
为了验证蒸发波导预测改正模型的精度,根据2020年10月在连云港和日照两个地方的海边利用微波折射率仪进行移动测量得到的蒸发波导实际测量数据,选择具有相同的波导高度ht、相同的地面大气修正折射率M0、不同的波导强度ΔM的典型数据。通过利用常用蒸发波导预测模型和改正模型计算得到大气修正折射率剖面,并与实际测量数据进行比较,得到了两种蒸发波导预测模型的代表性误差。
3.1 蒸发波导测量
2020年10月14-25日,在连云港和日照的海边分别进行了蒸发波导的测试。在实验中利用吊车作为测试平台,将高精度的微波折射率仪和激光测距机一起悬挂在吊车的升降线上进行上下移动测量,如图4所示,共获得大气修正折射率剖面1 500组数据。微波折射率仪的精度为0.5,采用的激光测距机的测距精度为2 mm。


图4 蒸发波导测试实验
3.2 两种蒸发波导预测模型的精度检验与分析
为了检验蒸发波导预测模型的精度,在所有测量数据中选择了具有相同地面修正折射率和波导高度,但具有不同波导强度的七组数据,分别采用蒸发波导预测模型和本文的改进模型进行大气修正折射率剖面计算,并与实测大气修正折射率剖面进行比较,典型结果如图5所示。
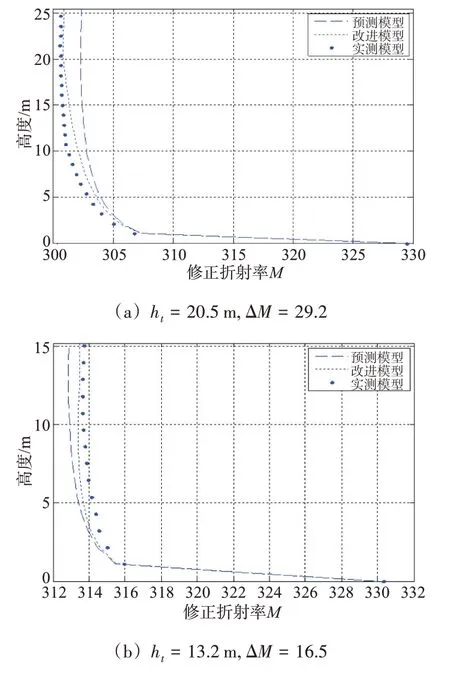
图5 蒸发波导预测模型精度比较
由图5可见,经与实际测试数据相比,蒸发波导预测的改进模型远远大于蒸发波导预测模型的精度,且在近海面低层和波导高度附近的精度很高,在海面与波导高度之间的中段误差较大。其原因是一旦海面大气修正折射率和波导高度确定后,由蒸发波导预测模型得到的大气修正折射剖面就得到确定,也就确定了波导强度ΔMt=M0-Mt。然而,实际环境中的波导强度很少正好等于ΔMt,会不同程度地大于或小于ΔMt,因此与实际大气修正折射率剖面相比就会产生一定的误差,引起误差的很大因素就是没有考虑波导强度的影响。当利用考虑波导强度的蒸发波导预测改进模型后,得到的大气修正折射率剖面与实际情况相比其误差很小,产生小误差的原因是受实际剖面的弯曲程度的影响。总的来讲,相比蒸发波导预测模型,改进模型的精度有了很大的提高。利用改进模型更能代表实际的大气修正折射率变化情况,更能适合于实际应用。
3.3 蒸发波导预测模型误差随波导强度的变化规律与分析
为了获得蒸发波导预测模型误差随波导强度的变化规律,在实际测量数据中选择了具有相同地面修正折射率和波导高度,但具有不同波导强度的七组数据,将利用常用蒸发波导预测模型和改进模型计算结果与实测数据进行差分,在波导高度ht为20.5 m 时得到蒸发波导预测模型误差随波导强度的变化规律,结果如图6所示。
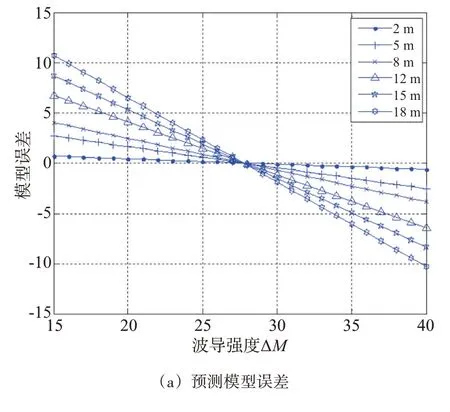
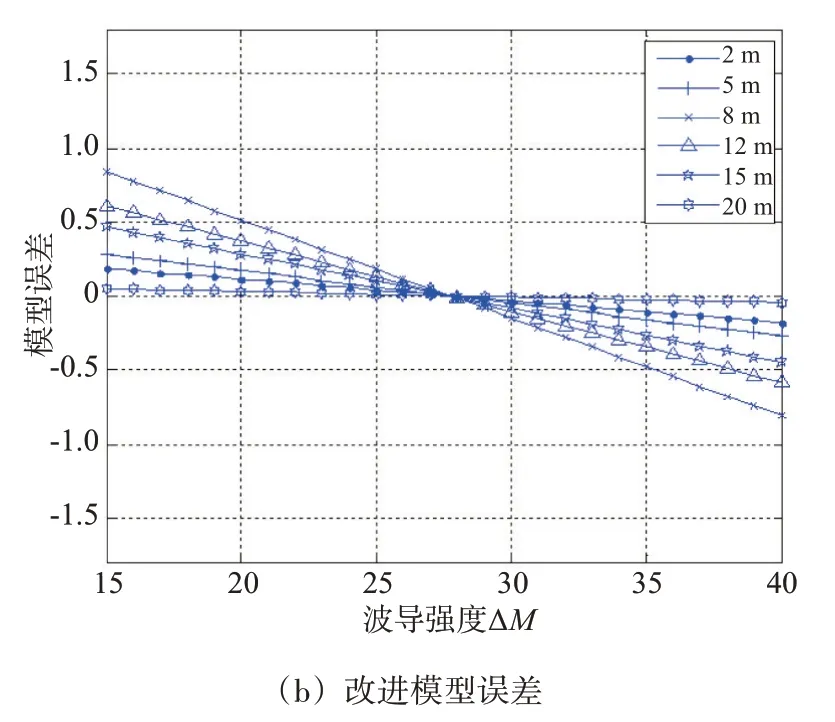
图6 蒸发波导预测模型误差随波导强度的变化
从图6可知,蒸发波导预测模型精度远远小于改进模型精度。与实测数据相比,预测模型和改进模型产生的误差随波导强度基本上呈线性变化。当实际波导强度等于预测模型的波导强度时,两种模型产生的误差都很小;随着实际波导强度偏离预测模型波导强度的增大,两种模型产生的误差也都逐渐增大,但是改进模型的误差远远小于预测模型的误差。
4 结束语
提高舰船雷达性能是现代战争的紧迫需求,利用蒸发波导效应实现雷达超视距探测是扩大雷达探测范围的重要方式之一。要实现舰船雷达超视距探测首先需要获得蒸发波导剖面,其中蒸发波导剖面建立的精度决定着雷达的实际有效应用。实验表明,本文提出的蒸发波导预测的改进模型可以有效地提高大气折射率剖面的精度,减少了常用预测模型带来的误差,更适合舰船雷达的实际应用,能够有效提高其利用蒸发波导进行超视距探测性能。下一步的主要工作是研究蒸发波导中大气修正折射率剖面的弯曲影响,建立更高精度的蒸发波导预测的实用模型,进一步提高蒸发波导的预测精度。
