高超声速目标尾迹对GNSS信号的衰减特性研究

冯世杰

（电子科技大学电子科学技术研究院，四川成都 611731）

0 引 言

临近空间（距离地面20～100 km 高度的区域）内的高超声速目标（如弹道导弹、航天飞机）再入或在临近空间中飞行时会与空气产生强烈摩擦，导致目标周围空气发生电离，形成包裹目标的等离子体鞘套及目标身后范围较大、强度较低的等离子尾迹，再入过程中的通信黑障便是由此产生［1-2］。洲际导弹等再入武器的等离子体鞘套会改变再入目标的雷达目标特性，从而对有源雷达的目标探测带来了一定欺骗和干扰作用。

等离子体鞘套及尾迹可能会对在其中传播的电磁波产生衰减、折射、反射等效应［3-4］。由于时域有限差分方法（Finite-Difference Time-Domain,FDTD）在色散介质的仿真计算中存在的独特优越性，被广泛用于等离子体的电磁模拟［5］。其中移位算子时域有限差分方法［6］因编程简单、概念清晰且计算精度高而受到较多关注［7-11］。但这些研究中，普遍使用二维鞘套模型，少有人对等离子鞘套进行三维建模仿真。

等离子体的电磁特性不利于有源雷达的目标探测，但可用于无源雷达对空间目标的探测。无源雷达，即自身不具备信号发射器，利用空间已有辐射源进行目标探测的雷达。基于GNSS 的无源雷达因具有成本低、信号源广泛、覆盖率高等特点，受到的关注日益增多。有研究发现，数类不同飞行器的飞行过程均会在短期内降低经过目标飞行路径上的GNSS 信号强度［12］。我国也有不少学者，在尝试利用GNSS 信号来进行空间目标探测［13-16］。但目前少有学者就高超声速目标尾迹对GNSS信号的衰减特性进行研究。

由上可见，针对等离子体鞘套电磁特性的数值仿真研究中大多使用二维模型，对鞘套内等离子体的三维分布重视不足。同时鞘套尾迹范围较大，对GNSS 信号的衰减作用明显，这些特征均十分适用于被动式目标探测，但现有研究对鞘套尾迹的关注较少。本文借助计算流体动力学（Computational Fluid Dynamics,CFD），模拟了高超声速再入体在临近空间飞行时的三维等离子体流场，建立了三维等离子体鞘套电磁模型，并使用改进的SO-FDTD算法，仿真计算了GNSS信号在目标不同飞行条件下的等离子尾迹中的功率透射系数，绘制了透射系数分布图。为基于GNSS 的被动式空间目标探测提供了一定依据。

1 目标绕流流场模型

图1所示为文中建立的高超声速目标模型，其中模型总长0.9 m，直径0.09 m，尾翼宽度0.045 m。在ESI_Group 软件中，使用基于热化学非平衡效应的七组元空气化学反应模型［17］和Park 双温度模型［18］，以全N-S方程组对再入体热化学非平衡流场进行求解，仿真计算不同飞行条件下的目标绕流流场。不同飞行条件下的背景大气密度、压强和温度等相关参量，参考美国标准大气模型（1976）进行取值。

图1 目标模型示意图

等离子角频率以及等离子碰撞频率是等离子体鞘套的两个重要参数，能够显著影响等离子体鞘套的电磁特性。由文献［4］，可基于仿真得出的流场参数计算等离子角频率和等离子碰撞频率，计算公式如式（1）、（2）所示：

式中：ωp为等离子角频率；ven为等离子碰撞频率；ne和nm分别为鞘套中的电子数密度以及中性粒子数密度；T为气体温度；me为电子质量，me=9.1×10-31kg；e为电子电荷量，e=1.6×10-19C；ε0为真空介电常数，ε0=8.85×10-12F/m。

利用式（1）、（2）对高超声速再入体绕流流场仿真结果进行计算，可得等离子体鞘套的电磁参数分布。绕流流场随目标飞行高度、速度、攻角等条件的变化而存在区别，但流场结构具有一定相似性，下面仅以海拔高度H=40 km、目标飞行速度V=20 Ma、攻角为0°的绕流流场为例进行说明。

图2、图3所示为再入模型绕流流场的参数分布。由图2和图3可知，等离子角频率及等离子碰撞频率在绕流流场头部达到最大值，在流场身部及尾迹区域显著下降。绕流流场在目标身后不断扩散，尾迹外侧的等离子角频率低于尾迹中心，同时尾迹外侧的等离子碰撞频率高于尾迹中心。

图2 Ma=20，H=40 km条件下的等离子角频率分布图

图3 Ma=20，H=40 km条件下的等离子碰撞频率分布图

2 电磁波传播的计算方法及模型

2.1 改进的SO-FDTD方法

本文通过移位算子时域有限差分方法（SOFDTD），对电磁波与等离子体鞘套的相互作用进行计算分析。在碰撞非磁化冷等离子介质中，Maxwell方程组及其辅助方程为

式中：J为极化电流密度；E为电场强度；H为磁场强度；ωp和νen分别为等离子角频率和等离子碰撞频率；μ0为真空磁导率，μ0=4π×10-7N·A-2。

假定J与E的离散空间坐标相同，E值更新于整数时间步，而J和H的值更新于半整数时间步，以x分量为例，可得式（3）、（4）两个旋度方程的FDTD差分离散格式为

引入移位算子［6］：

利用移位算子对式（5）进行化简得

式中：p0=p1=2ε0ω2p；q0=νen+；q1=2νen；q2=νen-2/Δt。

如果直接使用式（9）进行迭代计算，则程序内存开销较大，因为需要引入Jxn-1/2，Jxn-3/2，Enx和Enx-1四个辅助变量存储以前时刻的场分量。这里采用文献［8］中给出的内存优化算法，引入一个辅助变量Jx1，这样式（9）可由式（10）、式（11）所代替：

可见，利用式（10）、式（11）进行迭代计算，仅需使用1 个辅助变量Jx1即可，这种计算方式能够节约内存，特别是在三维模型中。但需注意的是，在计算式（10）之前，需用一个临时变量保存Jn-1/2x，以防在计算式（11）时变量被覆盖丢失。

2.2 电磁仿真模型的建立

SO-FDTD仿真程序中采用边长为0.007 5 m的立方体网格对等离子体流场进行建模，仿真程序通过Matlab 编写。SO-FDTD 电磁仿真模型整体为三维矩形，其中再入体模型的轴向平行于电磁仿真模型中的x轴，且再入体模型的轴向位置位于电磁仿真模型y-z平面的中心。因本文主要关注流场尾迹导致的电磁波衰减，所以电磁仿真模型在x轴方向上的仿真范围较大，为7 m，在y轴及z轴方向上仿真范围均为1.7 m。电磁仿真模型内共有49 916 846个网格，模型边界使用了10层CPML 边界。为了将CFD 计算得到的流场参数转换到SOFDTD 电磁仿真模型中，本文使用距离反比法进行了空间差值运算。由于仿真实验中的模型范围较大，网格数较多，为加快程序运行速度，在距离反比差值以及FDTD 迭代程序中均使用了GPU 并行加速技术。

在高度H=40 km，马赫数Ma=20，攻角为0°的飞行条件下，频率为1 575.42 MHz 的平面电磁波沿z轴正方向传播时，电磁波在绕流流场中的归一化电场幅度分布如图4所示。从图4中可以发现，在目标中轴线所处的x-y平面上，目标头身部区域附近的电场幅度分布出现了条纹状的“波纹”。这是由于高超声速目标头身部区域激波的存在，因此目标头身部区域的介质参数分布存在较大梯度，从而导致了入射电磁波的反射及折射现象。

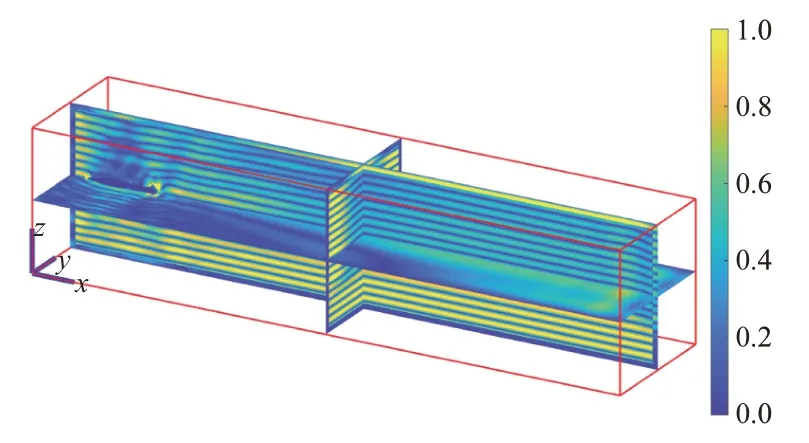
图4 平面波在绕流流场中的归一化电场幅度分布示意图

图5为模型中目标头身部x=0.75 m 处的y-z平面上的电场分布示意图。从图5可见，反射及折射后改变传播方向的电磁波又与原传播路径上的电磁波发生干涉，从而导致了图4中出现的“波纹”。

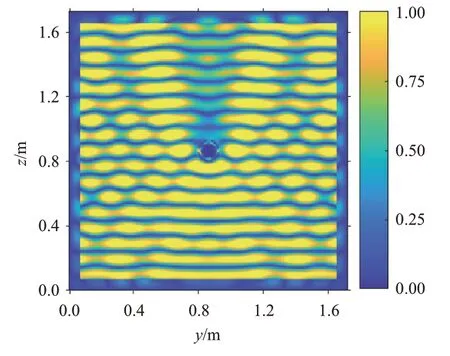
图5 目标头身部y-z平面切片上的电场幅度分布示意图

3 等离子体流场尾迹中的GNSS信号衰减特性

在仿真程序中，设平面电磁波沿模型z轴正方向传播。由于鞘套尾迹的范围较大，对GNSS 信号的吸收衰减更容易被探测发现，所以本文重点关注鞘套尾迹对信号的影响。图4所示结果的同等仿真条件下，模型中部x=3.50 m 处尾迹区域的y-z平面上的归一化电场分布图如图6所示。

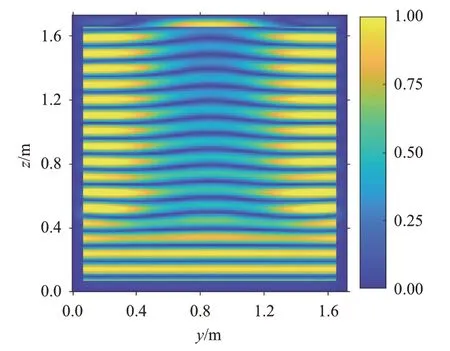
图6 目标尾迹中y-z平面切片上的电场幅度分布示意图

由图6可知，电磁波信号幅度在穿过等离子体鞘套后存在较明显的衰减，电场幅度的周期性变化在模型中z＞1.40 m 的区域内相对稳定。所以在本文的后续实验中，选择在z=1.60 m 处的x-y平面上对透射信号进行取样，该平面可称为取样面。信号经过等离子体流场后的衰减由归一化功率透射系数Pt量化，Pt由式（12）确定：

式中，Ei为入射波电场强度，Et为透射波电场强度。

3.1 信号频率变化的影响

设再入体飞行条件为：高度H=40 km、目标飞行速度V=20 Ma，攻角为0°。入射波频率f1设为北斗B2b 信号和伽利略E5b 信号所用的载波频率1 207.14 MHz；入射波频率f2设为北斗B1c 信号、GPS L1 信号和伽利略E1 信号所用的载波频率1 575.42 MHz。仿真得到的信号透射系数在取样面上的分布图如图7所示。

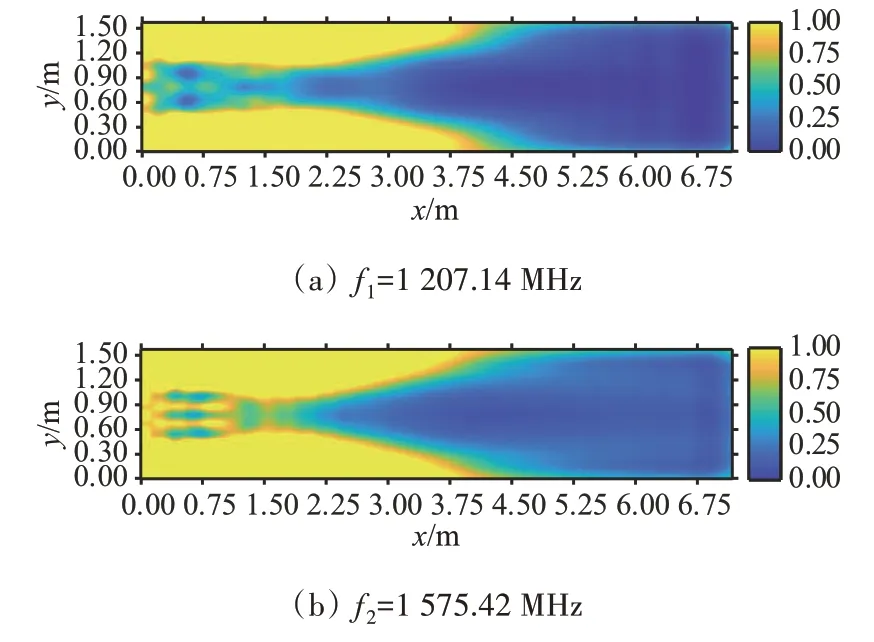
图7 不同频率GNSS信号的透射系数分布图

由图7可知，在本例给出的仿真条件下，GNSS信号经过高超声速再入体尾迹后的衰减较为明显，尾迹中心区域的透射系数在0.2 以下。同时在目标头身部对应的区域，透射系数的分布出现了3条相邻的凹陷区域，由图5可知这一现象同样由电磁波的干涉所致。

由图7（a）、（b）两图的对比可知，相同飞行条件下，频率更低的GNSS 信号经过鞘套尾迹后的透射系数更低，信号衰减更为严重。这是等离子体的高通滤波特性所带来的结果，只有入射电磁波的角频率大于等离子角频率时，入射波才能在等离子体中透射。

3.2 飞行速度变化的影响

设入射GNSS信号的载波频率为f=1 575.42 MHz，目标飞行高度H=40 km，攻角为0°，目标飞行速度V分别设为18、20、22 Ma，取样面上的透射系数分布如图8所示。

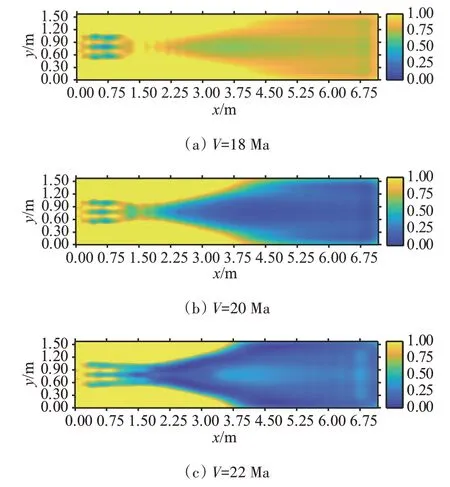
图8 不同飞行速度下GNSS信号的透射系数分布图

由图8可知，在其他条件相同时，尾迹中的信号透射系数随着飞行速度的增大而呈现整体下降的趋势，但它们之间并非简单的线性关系，透射系数的分布结构会随着飞行速度的增加而发生变化。在飞行速度为18 Ma 和20 Ma 时，取样面尾迹中心的信号透射系数低于尾迹边缘；而在飞行速度为22 Ma 时，情况相反，尾迹中部区域的信号透射系数不仅高于尾迹头部及边缘区域，甚至超过20 Ma飞行速度下相同区域的透射系数值。

上述现象，是不同运动速度条件下的流场参数分布差异所导致的。在相对低速（18 Ma、20 Ma）条件下，尾迹边界与中心的等离子碰撞频率差异不大，所以等离子角频率的分布决定了信号的衰减程度。由于尾迹中心的等离子角频率高于尾迹边缘，所以尾迹中心流场对透射信号的衰减作用更明显。但是在相对高速（22 Ma）条件下，流场尾迹边缘及头部的等离子碰撞频率加剧，由式（10）可知这些区域中等离子体对信号的衰减也随之增加。同时尾迹边界处碰撞频率的增加也一定程度上加快了气体分子复合速度，降低了尾迹中心区域的电子含量和等离子角频率，从而导致了尾迹中后段信号透射系数的回升。

3.3 飞行高度变化的影响

设入射GNSS信号的载波频率为f=1 575.42 MHz，飞行马赫数Ma设为20，攻角为0°，再入体飞行高度H分别设为35、40、45 km，不同高度下的大气参数如表1所示。

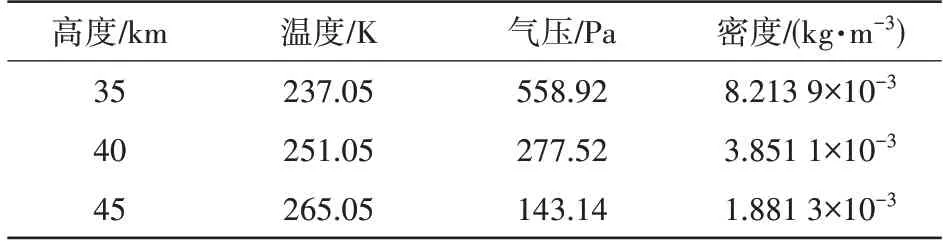
表1 不同高度下的大气参数表

不同高度下，GNSS 信号透射系数仿真计算结果如图9所示。

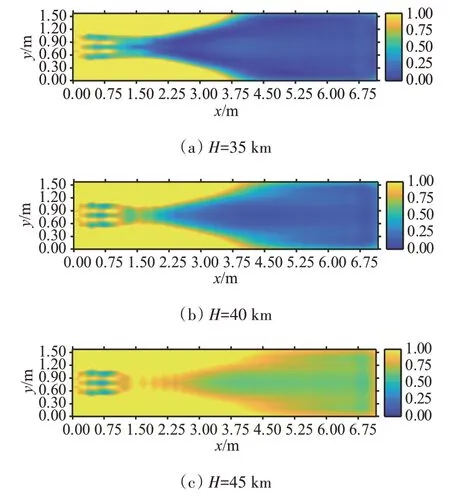
图9 不同飞行高度下GNSS信号的透射系数分布图

由图9可知，与3.2节中的现象相似，在飞行速度一定的情况下，尾迹中的信号透射系数随着飞行高度的降低而呈现整体下降的趋势，因为随着海拔高度的降低，鞘套中气体分子经高温电离产生的等离子体浓度也随之升高。但透射系数的分布结构会随着飞行高度的降低而发生变化。在飞行高度H为35 km 时，取样面尾迹中心区域的信号透射系数高于尾迹边缘及头部区域；而在飞行高度为40 km 和45 km 时，尾迹中心区域的信号透射系数低于尾迹边缘及头部。这与3.2 节中出现的类似现象有着相同的原因，即更低的飞行高度条件下，尾迹头部及边界处的等离子碰撞频率加剧，增强了这些区域对电磁波的吸收，也加快了尾迹中气体分子的复合速度，从而导致了信号透射系数分布结构的变化。

4 结束语

本文通过热化学非平衡模型模拟了导弹型再入体在临近空间飞行的绕流流场，并利用改进的SO-FDTD 方法对GNSS 信号在流场尾迹中的衰减特性作了计算和分析，得出了以下结论：

1）临近空间高超声速目标绕流流场尾迹能够给GNSS 信号带来明显的衰减。衰减特性因再入高度、速度、信号频率和取样点位置的不同而存在区别。

2）目标飞行条件一定时，频率越高的GNSS信号在绕流流场中的透射系数越高。

3）在其他飞行条件相同的情况下，高超声速目标运动速度增加或高度降低时，GNSS 信号透射系数呈现整体降低的趋势。但飞行条件变量与透射系数之间的关系并非简单的线性关系，透射系数分布结构会随着尾迹流场参数的变化而发生变化。

4）一般情况下，高超声速目标尾迹中部区域对信号的衰减效应强于尾迹边界及头部区域。但当其他飞行条件不变，目标飞行速度超过或飞行高度低于某临界值时，尾迹中部区域对信号的衰减效应会弱于尾迹边界及头部区域。

在未来的研究中，有条件的学者可利用风洞等试验设备对高超声速目标绕流流场进行参数验证。另外在后续电磁学仿真中，可增大仿真范围，并将目标外形、来流攻角、信号入射角度、信号的反射和折射纳入考虑，为基于GNSS 的高超声速目标无源探测提供更为坚实的依据。