土拱应力传递模型及其形态差异性对比*

林 斌 赵咏佳 李怀鑫,2 田竹华 王 鹏

(1. 安徽理工大学土木建筑学院, 安徽淮南 232001; 2. 长安大学公路学院, 西安 710064; 3. 马鞍山学院建筑工程学院, 安徽马鞍山 243100)

土拱效应是桩体支护工程的关键内容,土拱效应的存在使得桩侧土体内部应力发生了偏转且形成类似拱形的“虚拟拱”现象,工程中“以点控线,以线控面”的支护理念就是利用土拱效应的机理。实践表明,土拱效应的作用范围是影响桩体受力的关键因素。[1]为此前人进行了大量研究:文献[2-3]分别采用悬链线、圆弧线小主应力拱迹线描述土拱作用范围;吕庆等则采用抛物线型大主应力拱迹线分析土拱作用范围,[4]两者最主要问题是桩体受力时,桩后有无数条应力等值线,如何确定具体应力等值线为土拱作用范围,而且土拱效应受蠕变[5]、温度[6]、土体含水率[7]、动荷载[8]以及桩截面尺寸[9]等因素影响,不同影响因素会导致桩间土拱形态各异。在理论计算中,正是由于假定的土拱形态不同,从而导致各计算方法间的差异性较大。[10]

近些年来,随着PLAXIS、FLAC3D、ABAQUS等数值软件的发展,通过数值模拟分析土拱形态成为一种常用手段,张建勋等通过PLAXIS软件改变相关参数,阐述了土拱的作用范围以及土拱内应力的分布规律;[11]Li等通过FLAC3D软件分析了土拱效应的产生条件以及应力的传递过程;[12]刘朝晖等通过数值软件对桩间土拱效应进行研究,结果表明土拱形态不同则桩间结构物的受力状态也不同。[13]上述研究成果对研究土拱效应及土拱应力传递规律具有一定意义,但缺乏严格的数学模型进行定义。

因此,基于桩、土静力平衡条件及抗剪强度准则,将建立土拱应力传递模型,并基于工程背景建立数值模型,通过控制等应力差方法比较三种应力云图中土拱的形态差异,并结合模拟及相关研究成果对土拱应力的传递规律进行分析。

1 土拱应力

合理桩间距下,土拱效应不仅发生在水平方向,在竖直方向也会发生土拱效应,由于两者相互作用而发生耦合现象,因此为简化理论计算,假定竖直土拱为水平土拱起到拱脚支撑作用,其模型如图1所示。

图1 三维土拱效应模型Fig.1 Soil arching effect of three dimensions

1.1 竖向土拱

取某一深度z下单位厚度相邻抗滑桩间竖向土拱受力分析,其中p1与土体重力方向平行,p2平行于拱体某一点曲线斜率,桩间竖向土拱受力如图2所示。

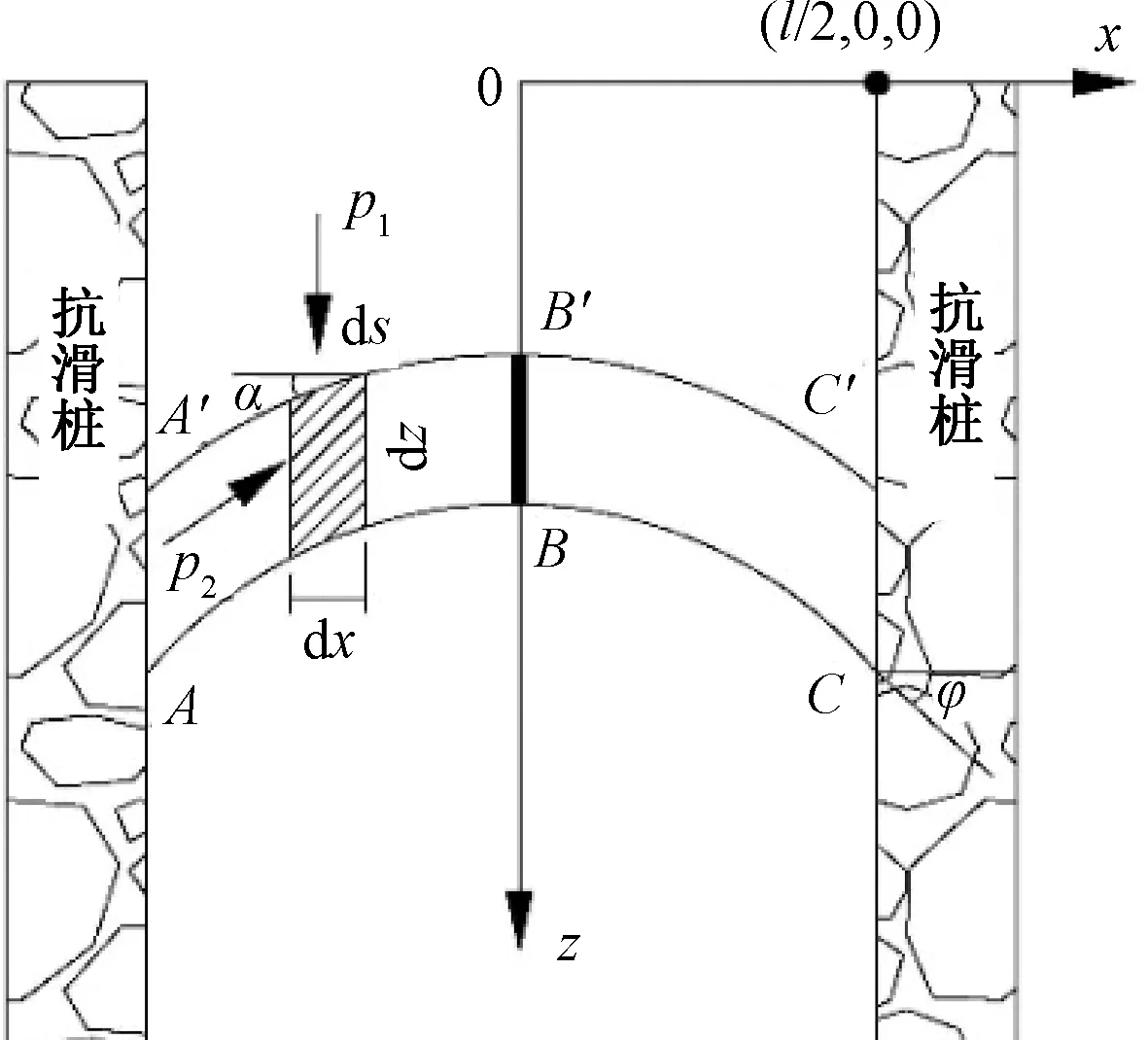
图2 竖向土拱整体受力分析Fig.2 Analysis of overall forces of vertical soil arching

模型假定桩体为刚性体,桩间竖向土拱所受的最大主应力σ′1为定值,且均匀竖直作用在竖向拱上。[14]竖向土拱拱顶B′B截面处受力分析如图3所示,拱顶B′B截面处存在p1=σ′1,p2=σ′2,σ′1为最大主应力,σ′2为中主应力,σ′3为小主应力。

图3 竖向土拱拱顶竖向剖面Fig.3 A vertical cross section at the apex of vertical soil arches

根据图2竖向土拱微元体分析可得:

(1)

式中:τyz和σx分别为微元体侧面的剪应力和正应力;c为黏聚力;α为微元体所在拱迹线处的切线方向与水平方向的夹角。

根据微元体静力平衡条件,由式(1)可得:

p1=p2·2sinα+2c

(2)

由于拱表面的应力均匀分布,即σ′1为:

(3)

由式(1)～式(3)可知:

(4)

在竖向拱与桩体接触面处α=φ。

竖向拱体上方合力为:

(5)

式中:l为拱的跨度。

根据图2竖向土拱整体静力平衡条件可得:

(6)

将式(4)代入式(6)中可得:

(7)

求解式(7)可得:

(8)

1.2 水平土拱

对于抗滑桩而言,桩间x—z平面内竖向土拱为x—y平面内水平土拱提供了拱脚支撑,此时桩侧x—y平面内水平土拱受力如图4所示。

图4 桩后端承拱微元体受力分析Fig.4 Force analysis on soil elements of end bearing arches behind piles

根据水平方向整体静力平衡条件推导σ′3时,应不考虑土体质量,由式(7)得:

(9)

求解式(9)得:

(10)

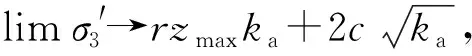
将该边界条件代入式(10)中得:

(11)

2 水平土拱应力递减模型

沿桩长方向取单位水平土拱为研究对象,假定极限状态下,土体抗剪强度满足Mohr-Coulomb强度理论,且桩后水平推力经过水平土拱自我调整后分别作用于桩后拱脚处和桩侧土拱上,如图5所示。

由图5可得:

(12)

式中:b为桩正面宽度;σ″3为桩后拱脚处应力;σ′3为桩侧土拱上应力。

由图5可知桩角处应力满足:

σ′3=σ″3cosβ

(13)

式中:β为拱迹倾角;不考虑土体黏聚力时可假定为φ、45+φ或45-φ,若考虑黏聚力影响时则假定[15]:

(14)

式中:h为拱厚。

桩土界面达到极限剪切强度时满足Mohr-Coulomb准则,即:

τxy=σxtanφ+c

(15)

式中:τxy为桩土界面剪应力;σx为桩土界面法向应力。

通过图6将坐标系向左平移ccotφ,进而将式(15)转换成式(16)[16]:

图6 Mohr-Coulomb 强度准则Fig.6 Mohr-Coulomb Strength Criterion

τxy=(σx+ccotφ)tanδ=σx1tanδ

(16)

根据坐标系平移建立误差分析可得:

(17)

将式(17)代入式(16)可得:

tanδ(σy+ccotφ)

(18)

该方法虽可建立桩-土界面抗剪强度关系,但由于计算复杂,因此可采用等应力模型转换,将式(15)转变成式(19)[17]:

τxy=σysinφ+ccosφ

(19)

由图4可知桩侧端点处应力分别为:

(20)

由于σ′3随y从σ′3减小至零,且τxy与σy为线性关系,故假定桩侧剪切面上τxy随σy呈线性递减的关系,相关研究成果表明桩侧应力呈线性递减变化[6],因此可得:

(21)

联立式(12)、式(20)和式(21)可得:

σ3=k(φ)σ″3+d(φ,c)

(22)

由式(13)、(22)可得桩后土拱和桩侧土拱的荷载传递系数分别为:

式中:α1为桩后土拱荷载传递系数;α2为桩侧土拱荷载传递系数。

3 数值模拟

3.1 模型参数

四川省境内巴(中)达(州)铁路D1K70 +390～DK70 +420右侧边坡[1],坡体相对高差为30～120 m,坡体介质主要为风化泥岩残积土,边坡模型38 m高,52 m长,24 m宽,土体内摩擦角φ为28°,黏聚力c为50 kPa,桩截面尺寸为b×a=2 m×3 m,桩长为16 m,其中悬臂段长为9 m,桩间净距l为6 m,模型相关参数见表1,网格划分单位均为1 m,模型边界采用单向约束,桩体固定,模型共计42 480个单元,47 192个结点,模型见图7。

表1 模型参数Table 1 Model parameters

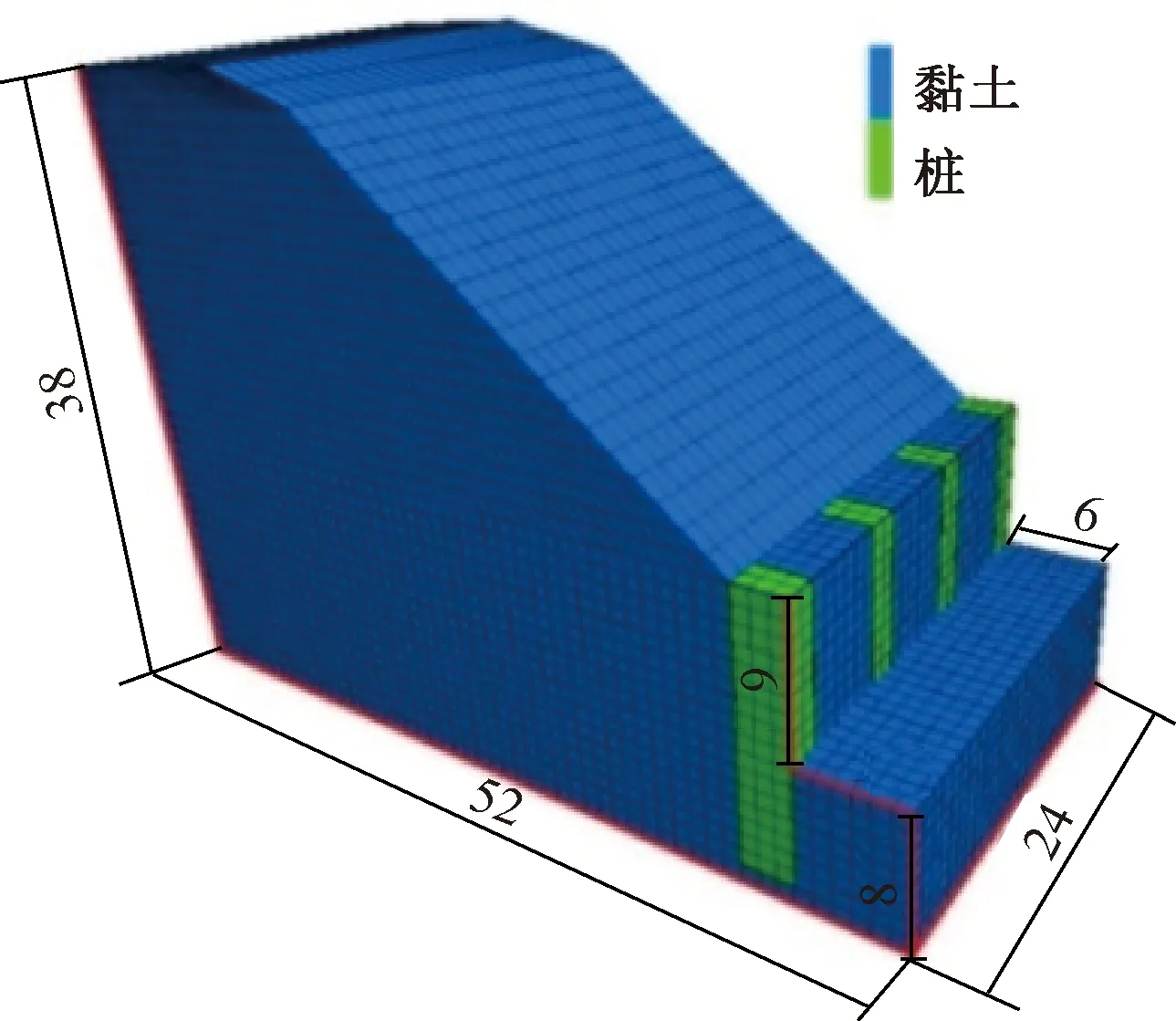
图7 FLAC3D三维模型 mFig.7 FLAC3D modeling

3.2 土拱效应演化过程

为比较不同应力工况下土拱形态差异性,将FLAC3D中的模型结果导入到Tecplot软件中,通过定量控制等应力差方法比较不同深度下的模型切片,应力云如图8所示,其中σyy代表y方向应力,σ1代表大主应力,σ3代表小主应力。

a—距桩顶1 m; b—距桩顶3 m; c—距桩顶5 m。图8 三种应力工况下土拱效应区域 MPaFig.8 Zones of soil arching effect in three conditions of stress

从图8可见:随着桩深的增加,桩间最先形成一级拱,一级拱应力达到一定值后,二级拱开始形成,当上一级拱承受应力达到极限时则退出工作状态,此时桩后荷载由次级拱承担,因此次级土拱承受应力大于初级土拱承受应力,而土拱承受的抗剪强度有限。为简化理论分析,假定一级拱作用区域为土拱主要作用范围,该范围距桩体的最大距离作为最大拱高fmax,各级拱高随桩深的变化如图9所示。

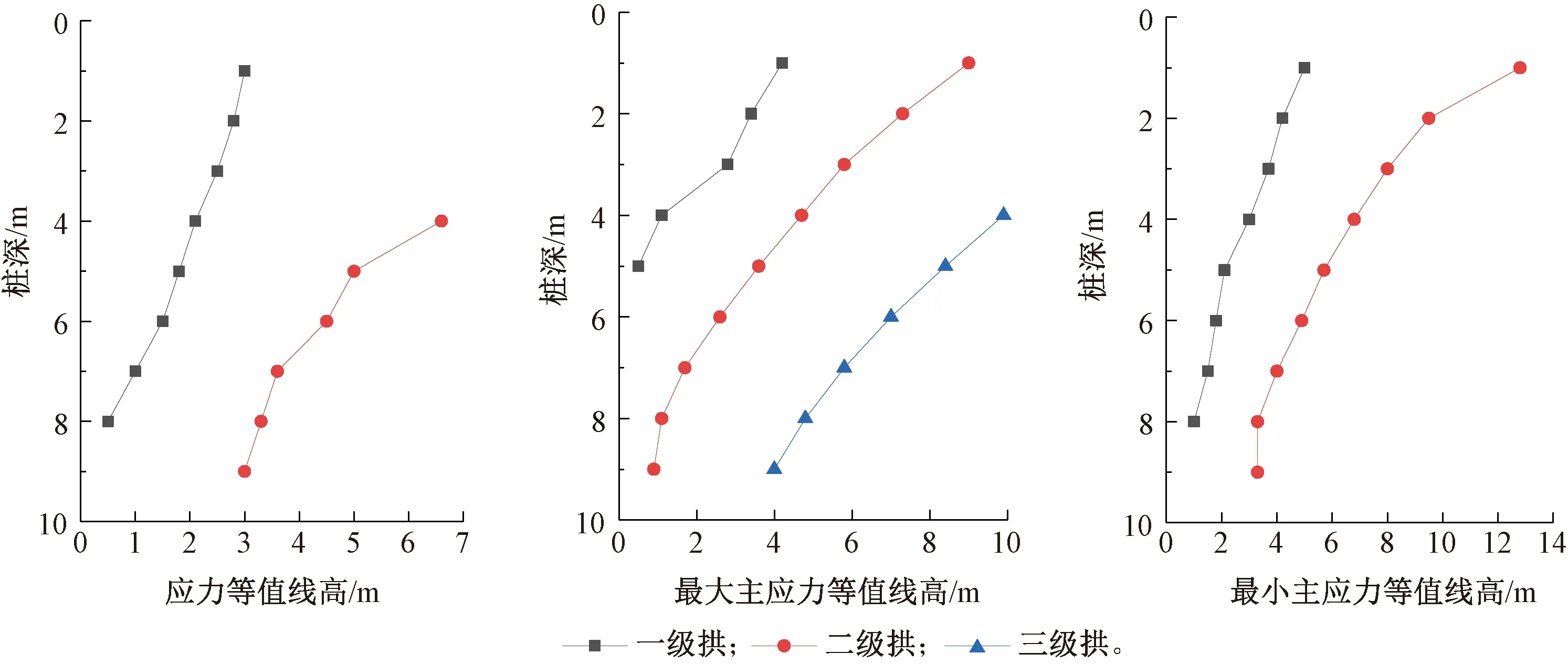
图9 三种应力云等值线高Fig.9 Isoline heights of three stress contours

由图9可看出:各级拱高均随桩体深度的增加而减小,一级拱最先消失,而且一级拱拱高下降速率大于二级拱拱高,此外,最小主应力云的最大拱高大于最大主应力云的最大拱高,而最大主应力云的最大拱高大于应力云的最大拱高。

相关研究学者以相邻圆形抗滑桩轴线及中心线建立坐标系,提出了桩后最大拱高与桩间距、桩体截面尺寸、桩深的关系的经验表达式[18]:

fmax=λD(n+1)-0.375λz

(24)

式中:fmax为最大拱高;λ为与桩土性质有关的系数,黏性土取1;D为圆形抗滑桩直径;n为桩间距与桩径的比值;z为深度。

在合理桩间距下,桩后荷载主要通过土拱效应传递到抗滑桩,但由于土拱效应作用范围随桩深变化,因此很难确定具体拱迹线方程,根据水平土拱在竖直方向的演化过程,建立如图10所示土拱受力区。

图10 土拱效应分区Fig.10 Subregions of soil arching effect

由图8、图10可知:在y方向应力云中,桩后土拱效应作用范围只有Ⅰ、Ⅱ和Ⅳ区域,在大、小主应力云中,桩后土拱效应作用范围为4个区域。

3.3 土拱受力分析

现通过FLAC3D软件提取抗滑桩中线轴线处最大主应力云,如图11所示。可见:在大主应力云中土拱效应存在一定深度以下,进而桩间竖向土拱可为水平土拱提供拱脚支承,因此文中理论假设是可行的,此外,文中竖向应力σ′1是基于土拱效应提出的,即在合理桩间距下推导,因此将工程案例中相关参数代入式(8),建立合理桩间距下竖向应力σ′1与深度z间的关系,如图12所示。

图11 桩间大主应力云 PaFig.11 Contours of vertical stress σ′1 between piles

图12 合理桩间距下竖向应力σ′1Fig.12 Vertical stress σ′1 with reasonable pile spacing

由图12可以看出:在合理桩间距下,桩间距越大,土拱效应越微弱,竖向应力σ′1随深度变化越大,反之则越小,因此在合理桩间距下计算竖向应力σ′1时,不能够忽略竖向土拱效应的影响。

为进一步分析水平土拱应力传递规律,将案例中相关参数及不同应力云中的拱高值代入式(11)可得桩间水平应力分布,如图13所示。

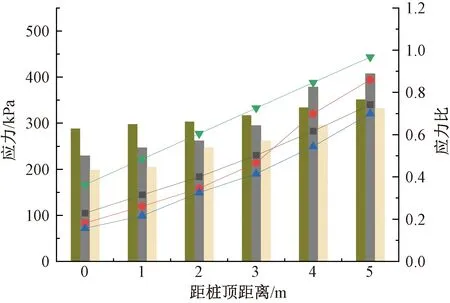
图13 桩间水平应力σ′3分布Fig.13 Horizontal stress σ′3 between piles

对比可以发现:随着桩体深度的增加,桩间水平土拱应力逐渐增加,其占桩后应力的比值也逐渐增加。在深度较浅时,桩后荷载主要由桩后水平土拱和桩侧水平土拱承担,其中桩后水平土拱作用在桩正面处,桩侧水平土拱作用在桩侧,随着桩体深度的增加,桩后水平土拱逐渐失效,荷载主要通过桩间水平土拱作用在桩侧,因此水平土拱应力σ′3增加并逐渐接近于桩后应力σ3。

将不同深度下桩后拱脚处应力σ″3代入式(11)中可得不同深度下桩脚处应力,如图14所示。可见:数值结果中桩后拱脚处应力随深度变化不大,由于式(10)时按Rankine土压力计算C1,从而造成与实测值间误差,但根据后者桩体一般偏于安全。当设计桩体时不考虑土拱效应时,根据Rankine主动土压力值设计桩体强度比考虑土拱效应时土压力值所设计桩体强度偏大。

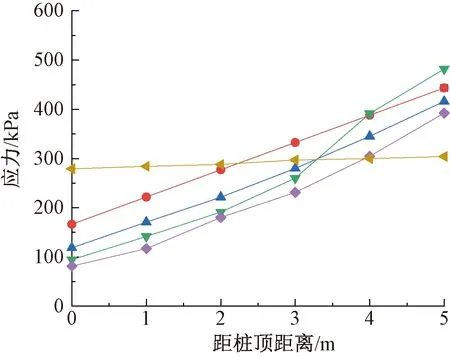
图14 桩后拱脚处应力σ″3Fig.14 Stress σ″3 in arch feet behind piles

为比较土拱效应下荷载的传递规律,将桩后拱脚处不同深度下应力σ″3代入式(23)可得到桩后荷载的传递规律,如图15所示。

图15 水平荷载传递系数Fig.15 Transfer coefficients of horizontal loads

桩侧荷载传递系数逐渐增大,但桩后土拱荷载传递系数逐渐减小,这表明荷载逐渐从桩后土拱转移到桩侧土拱上,由于该算法只须监测桩后拱脚处的应力,在工程中易实施。

现根据数值模拟结果提取不同深度下桩侧平均剪应力,并将该平均剪应力代入(12)和式(21)可得到数值模拟下的土拱荷载传递系数,其与图15的对比结果见图16。

图16 土拱荷载系数理论计算与数值计算对比Fig.16 Comparisons between theoretical calculations and numerical calculations of soil arch load coefficients

由图16可以看出:土拱荷载系数的数值计算与理论计算的差异性随桩深逐渐减小,但两者结果整体较为接近,因此说明文中土拱荷载传递系数理论计算方法具有可行性。

4 结束语

1)桩间竖向土拱和桩后水平土拱的法向应力解析解均呈指数递减规律,这种基于桩侧摩阻力及桩土Mohr-Coulomb强度准则的计算方法消除了理论计算中由于假定拱迹线不同带来的结果差异性。

2)随着桩体深度的增加,水平土拱效应逐渐减弱,桩侧土拱法向应力σ′3及桩脚处应力σ″3均增加并逐渐接近桩后应力σ3,此外,桩后土拱荷载传递系数α1逐渐减小,桩侧荷载传递系数α2逐渐增大。

3)通过模拟桩后水平土拱效应的演化过程,可根据应力等值线构成的拱形结构将其范围分成为4个区域,其中Ⅰ区域范围内土拱效应最强。

4)同一条件下,最小主应力云中最大拱高拱高fmax大于最大主应力云图中最大拱高,而最大主应力云图中最大拱高大于水平方向应力云中的最大拱高,而且随桩体深度的增加,三种应力云中的拱迹线均发生变化,因此应建立与深度有关的拱迹线方程。