火灾下箱板装配式钢结构温度分布规律研究*

薛 辰 李 然 兰 涛, 余志祥 李泽旭

(1.中国船舶重工集团国际工程有限公司, 北京 100121; 2.西南交通大学土木工程学院, 成都 610031)

0 引 言

箱板式钢结构作为一种新兴的装配式钢结构体系,在强度、整体性、延性、抗震性能等多方面都具有很大优势。[1-6]该结构借鉴了船舶上层建筑形式,此体系的房屋建筑单元由加劲钢板装配而成,内部无梁柱,建筑单元具有模块化集装特征,构件连接及单元装配均采用干连接。该结构中的围壁墙板和楼板均由带加劲肋钢板制造而成,两者经装配形成承载系统以承担结构中的水平荷载和竖向荷载。该体系可充分利用室内空间,具有生产工业化、施工装配化、装修一体化等特点,现已应用于实际工程,详见图1、2所示。由于该体系为纯钢结构,耐火性较差,火灾作用下的高温对带加劲肋钢板的传热、受力等性能将产生较大影响,因此,须要明确箱板装配式钢结构在火灾作用下的温度场分布规律,为经济合理设计箱板式钢结构提供安全保障。

图1 箱板装配式钢结构办公楼示范工程Fig.1 A demonstration project of prefabricated box-plate steel structure office buildings

图2 箱板装配式加劲钢墙板与钢楼板Fig.2 Stiffened wall panels and steel floor slabs of prefabricated box-plate steel structures

现有的模拟火灾空气温度场的计算模型主要有经验模型、区域模型和场模型。经验模型中,当前采用最多的是1991年国际标准化组织ISO给出的标准温度-时间曲线[7]。该曲线虽计算方便,但由于未考虑火灾中各因素的影响,计算结果与实际情况差距大。区域模型可将结构进行合理分区,计算效率高,但其应用场景有限,在计算复杂空间场景时该方法将失效。目前计算最精确、最先进的是场模型,因此主流的流体软件FDS、FLUENT和CFX等都采用场模型,其计算精确高效,更接近真实火灾情况。李国强团队基于FDS软件模拟了120余例大空间建筑火灾温度场,拟合出适用于大空间建筑的空气升温简化模型算式[8-9],该算式已被CECS 200∶2006《建筑钢结构防火技术规范》采用。

目前对于截面均匀分布的钢构件的升温已有多种计算方法可求解,但对截面非均匀分布的钢构件升温,二维非稳态传热问题的解析解求解非常困难,通常采用数值方法。Palm使用通用有限元软件ABAQUS,考虑热传导、热对流、热辐射的综合因素,对各种结构构件进行三维瞬态热分析,得到结构构件在火灾下的温度分布[10],计算结果与文献[11-12]的计算结果相比较,显示有限元方法的精度令人满意。

目前对该新型结构体系的抗火性能研究较少,此体系在火灾作用下的耐火极限、临界温度、破坏模式等方面的研究尚处于空白,因此有必要对其在火灾下的热力学行为开展研究,为箱板式钢结构抗火设计提供参考依据。为此,以一个模块单元组成的单层箱板结构和三个模块单元组成的三层箱板整体结构为研究对象,通过数值模拟软件建立火灾动力学模型及火灾瞬态热分析模型,以火源位置变化为参数开展了7种火灾场景数值模拟,得到了不同火灾场景下空气温度场的分布规律及整体结构的传热历程数据。

1 模型概况

选择火灾动力学软件FDS,采用场模型建立了一层和三层的箱板式钢结构火灾动力学模型,进而根据火灾空气温度场结果,导入ABAQUS构建一层和三层箱板装配式钢结构火灾瞬态热分析模型。

1.1 空气温度场模型

1.1.1模型建立

建立的FDS模型以真实结构为依据,最大程度还原了真实结构,钢板墙内外两侧和楼板下方都设有均匀分布的横、纵向加劲肋。结构平面尺寸为9.7 m×8.3 m,层高为2.9 m,三层总高为8.7 m,墙和楼板均采用Q235,厚度均为1 cm,T形、L形加劲肋均匀分布于墙板与楼板内侧,L形加劲肋采用┗75×50×8,T形加劲肋采用TN200×200。所有的门窗洞口都处于常开的状态,用于模拟热气流的传导和烟气的扩散。取箱板装配式钢结构体系的单层单间和三层单间为研究对象,该结构功能为办公室,室内未采用喷淋防火措施。

为包含整个建筑物,单层模型建立的网格尺寸为11.0 m×10.0 m×5.0 m,总容积达550 m3,占地面积为110 m2。为确保其计算的稳定性和精确性,将整个建筑模型统一划分网格,最后选用0.1 m×0.1 m×0.1 m的单元格,最终网格个数为550 000个,模拟火灾时间为1 800 s,单次模拟计算时间大约需100 h。三层模型网格尺寸为11.0 m×10.0 m×10.0 m,模拟火灾时间为1 800 s,单次模拟计算时间大约需200 h。

1.1.2火源设定

大量火灾试验数据显示,在火灾初期增长阶段,热释放速率近似按时间的平方(t2)规律发展,简化之后可以式(1)[13]表示:

Q=αt2

(1)

式中:Q为火源热释放速率,kW;α为火灾增长系数,kW/s2;t为火灾有效燃烧的时间,s。

火灾的火源按照固定型火源场景设置,选取火灾类别为快速火,根据文献[13]取火灾增长系数α=0.044。该建筑的使用功能是办公室或住房,无喷淋,按GB 51251—2017《建筑防烟排烟系统技术标准》[14]中取稳态时最大热释放速率为6.0 MW。取固体稳定火源面积为单位面积1.0 m×1.0 m,将其布置在木质桌面上,设定其单位热释放速率为6 000.0 kW/m2,根据式(1)可计算得到,在t=358 s时将达到最大热释放速率。

因模型是按固定型火源设置,所以火源位置是影响箱板式钢结构建筑室内温度场分布的关键因素。当火源居中时,四周钢结构同步受热升温;但当火源在室内一侧时,靠近火源的钢构件会更快速地进入危险状态,钢构件失效顺序也会发生变化。为了研究不同火灾场景下该结构的失效过程和破坏机理,设置了不同的火源场景来探究不同工况下的火灾对空气温度场的影响,7种不同火灾场景工况见表1,单层模型的火灾场景工况示意见图3,室内空间的9个分区示意见图4。

表1 火灾场景工况Table 1 Fire scenarios of a single-storey prefabricated box-plate steel structure

a—三维示意; b—正视图; c—俯视图。图3 单层箱板装配式钢结构FDS模型Fig.3 A FDS model of a single-storey prefabricated box-plate steel structure

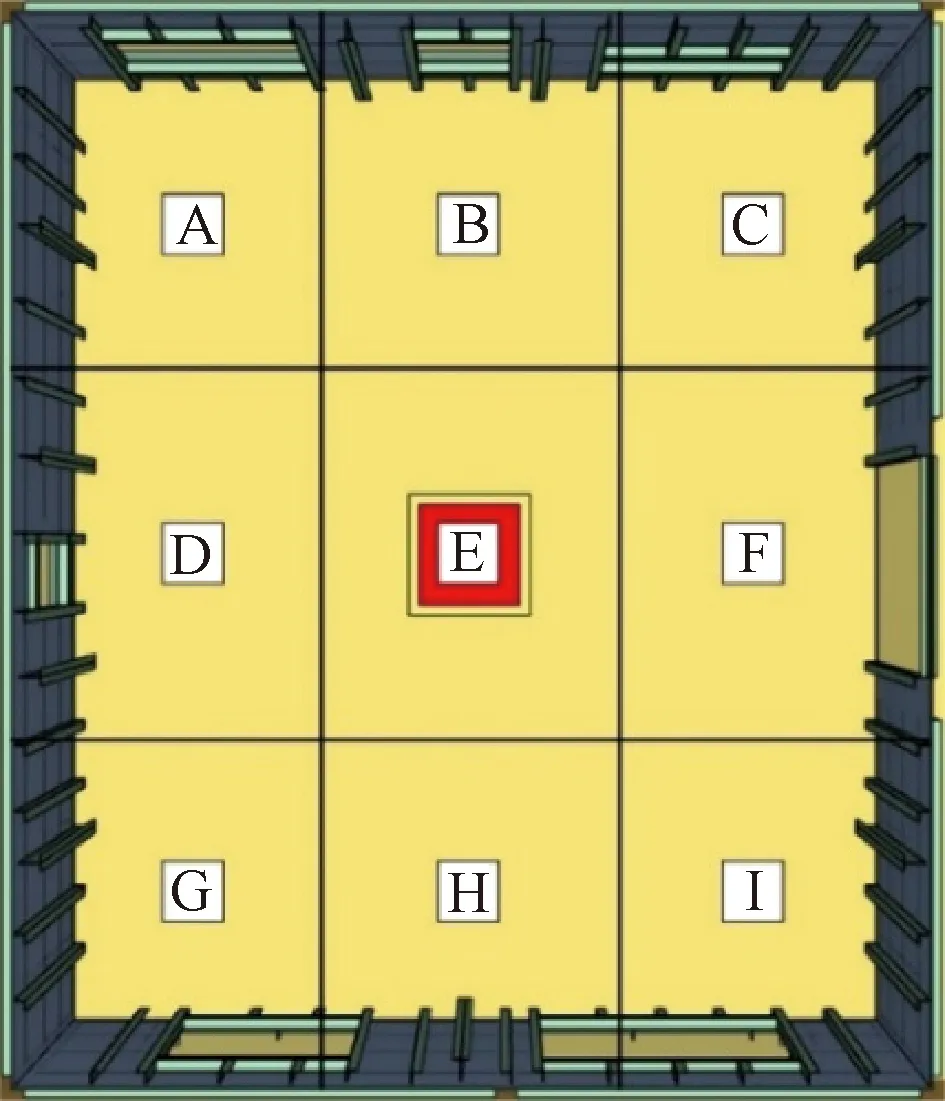
图4 空间分区示意Fig.4 A schematic diagram of space partition

1.1.3测点布置

为了获得火灾下整个室内的温度场,须要在关键位置设置足够的热电偶来测量火灾过程中的温度及其他参数的变化。为此,设定一层地面标高为Z=0 m,分别在Z=0,1,2,2.9 m高度平面内,室内空间A～G区每个区域的中心处各设置一个热电偶,在特殊位置如门窗洞口和墙面上也设置了部分温度测点,共计68个。另外为了更直观展示火灾发展过程中温度分布情况,在模型X、Y方向剖面以及Z=1,2,2.9 m高度平面处设置了温度切片。三层测点设置在每层中间高度和楼板处,分区情况与单层结构相同。

1.2 火灾瞬态热分析模型

1.2.1模型建立

火灾瞬态热分析模型的规格尺寸与前述FDS火灾模型一致,结构平面尺寸为9.7 m×8.3 m,单层高为2.9 m,三层总高为8.7 m,墙板厚为1 cm,楼板厚为1 cm;T形、L形加劲肋均匀分布于墙板与楼板内侧,L形、T形加劲肋截面分别采用L75×50×8和TN200×200×8×13,墙板外部的加强区由矩形肋纵横分布交错组成,截面为100 mm×10 mm;所有钢材均采用Q235;模型中所有钢构件间的连接均为刚接,边界条件为底部全部固接;热力耦合计算前施加的恒荷载为自重,活荷载为楼面荷载和上人屋面荷载,楼面荷载与上人屋面荷载大小为2.0 kN/m2。

1.2.2材料属性

通过比较分析各国设计标准关于钢材高温材性的关键参数取值,最终确定了本文数值模型的有效热物理参数及材性力学参数。钢板和加劲肋材料均为Q235钢,常温下屈服强度为235 MPa。热物理属性密度取ρs=7 850 kg/m3;热膨胀系数取αs=1.4×10-5m/(m·℃);比热容和热传导系数使用欧洲Eurocode 3[15]中的算式;泊松比取νs=0.3;屈服强度、弹性模量都按GB 51249—2017《建筑钢结构防火技术规范》[16]提供的算式进行计算,应力-应变关系使用Eurocode 3中提出的不考虑强化的光滑曲线材料模型为计算模型,输入每个温度下对应的应力-应变曲线。

1.2.3单元类型与分析步设置

瞬态热分析计算需要在接触板块中输入热辐射和热对流参数,并导入FDS中计算的测点随时间变化的温度数据。因火灾模型只考虑初期增长阶段及持续平稳的全盛阶段过程,所以1 800 s后的火灾视为已进入平稳阶段,之后的测点温度将使用火灾发展平稳阶段的温度数据。采用DC3D8热传导网格,通过瞬态热分析即可以得到结构受热后的温度时程数据。共设置一个分析步,属性为瞬态热传导,设置为自动调整步长,最大步长为30 s,计算时长取10 800 s。

2 空气温度场计算及分析

2.1 单层模型

2.1.1室内整体温度场分布

为方便观察火灾下室内空间空气温度场的分布规律,更直观地呈现火灾变化趋势,截取了不同场景计算结果,如图5～7所示,图中体现了火源处X、Y、Z方向的温度变化、烟气浓度和火势变化。

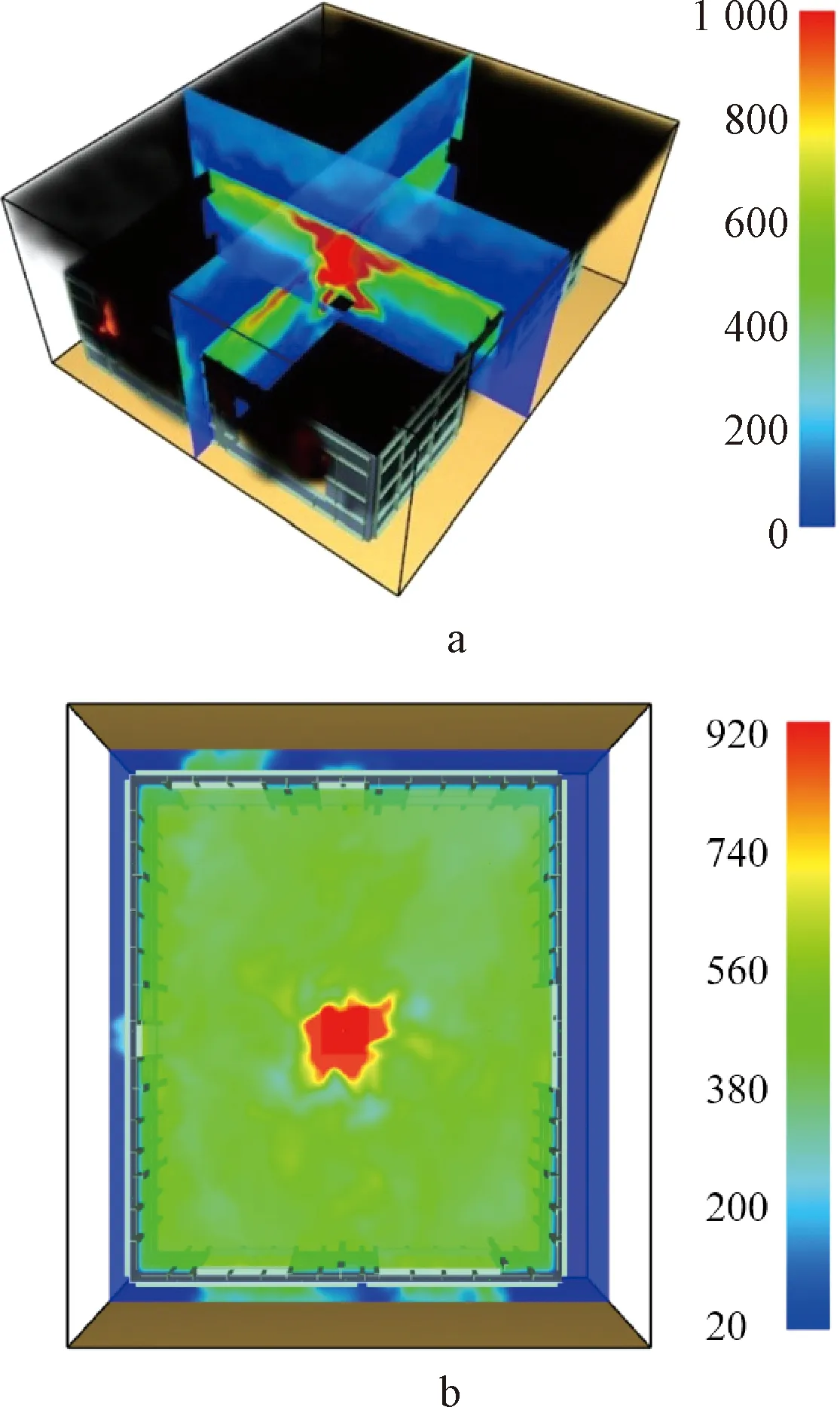
a—竖直方向; b—水平方向(Z=2.0 m)。图5 火灾场景1不同方向温度场分布 ℃Fig.5 Temperature fields in different directions in scenario 1

a—竖直方向; b—水平方向(Z=2.0 m)。图6 火灾场景2不同方向温度场分布 ℃Fig.6 Temperature fields in different directions in scenario 2

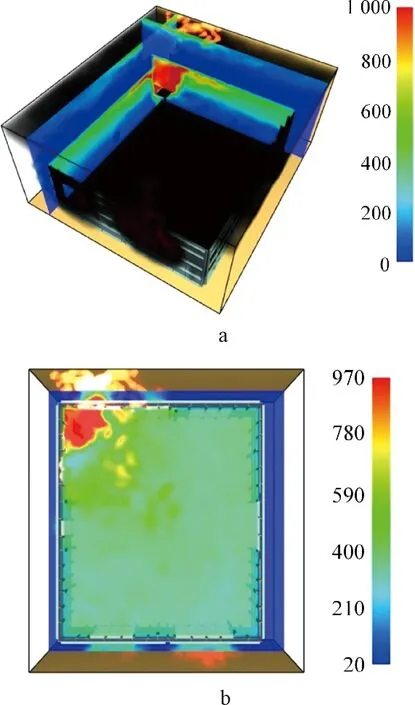
a—竖直方向; b—水平方向(Z=2.0 m)。图7 火灾场景3不同方向温度场分布 ℃Fig.7 Temperature fields in different directions in scenario 3

2.1.2测点温度-时间曲线

3种火灾场景下各测点时间-温度曲线如图8～10所示。由于火源位置的不同,场景1～场景3高温所对应的区域分别为E区,D区和A区。场景1和2中环境最高温度都达到了1 000 ℃以上,场景3温度偏低,最高温度约为900 ℃。

a—Z=2.0 m; b—Z=2.9 m。 A; B; C; D; E; F; G; H; I。图8 火灾场景1各测点温度-时间曲线Fig.8 Temperature-time curves of measurement points in scenario 1

a—Z=2.0 m; b—Z=2.9 m。 A; B; C; D; E; F; G; H; I。图9 火灾场景2各测点温度-时间曲线Fig.9 Temperature-time curves of measurement points in scenario 2

a—Z=2.0 m; b—Z=2.9 m。 A; B; C; D; E; F; G; H; I。图10 火灾场景3各测点温度-时间曲线Fig.10 Temperature-time curves of measurement points in scenario 3

整体来看,三种场景下的时间-温度曲线都呈现出离火源位置越近温度越高的趋势。从图8a、b中可以看出:灭灾场景1高度2.0 m处,E区后期温度稳定在1 050 ℃,除火源外,其余分区温度维持在400～500 ℃,E、A、B、G、C区呈现相似的变化趋势,在1 000 s附近温度突增。这是因为1 000 s左右时桌子腿被引燃,释放出了更多的热量;高度2.9 m处,除E分区外,D和F区温度较高,稳定阶段温度分别维持在670,600 ℃,其余分区则在500 ℃以下。场景2中,高度2.0 m处除火源区D区外,其余分区都经历了先两次升温,后进入稳定阶段,之后降温,再次进入稳定状态的过程,各分区温度-时间曲线如图9a所示;高度2.9 m处温度基本没有突变,如图9b所示,Z=2.0,2.9 m最后稳定阶段各分区温度见表2。场景3中,高度2.0 m处的曲线除火源外的区域温度变化较为一致,维持在300～400 ℃,2.9 m处时除火源外,温度最高的分区为D、E区,最高温度达到600 ℃,之后分别稳定在320 ℃和430 ℃,B、C、F、G区变化趋势较为一致,最后都稳定在340 ℃左右,其他距离较远的分区则在30 ℃以下。从图中也可以看出,空间位置越高的测点,曲率越缓和,体现了屋顶热空气慢慢积聚的过程。

表2 场景2各分区稳定阶段温度值Table 2 Temperatures of each part in scenario 2 in the stable phase of heating

2.2 三层结构

2.2.1室内整体温度场分布

4个火灾场景在燃烧相对稳定时的整体温度场分布结果如图11～14所示,图中体现了火源处X、Y两竖直方向及火源上方屋顶Z平面的温度分布。

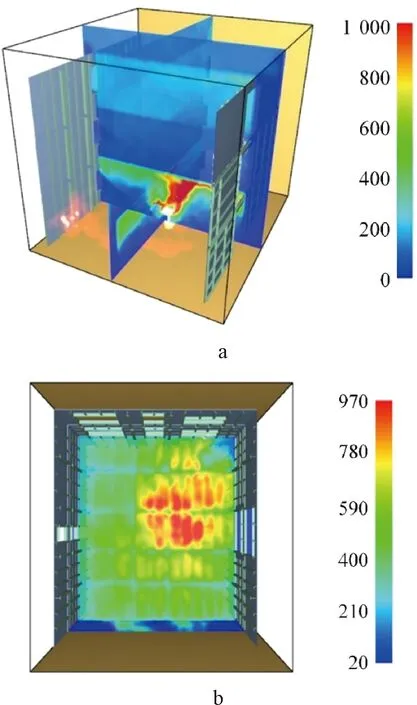
a—竖直方向; b—水平方向(Z=2.9 m)。图11 火灾场景4温度场分布 ℃Fig.11 Temperature fields in different directions in scenario 4

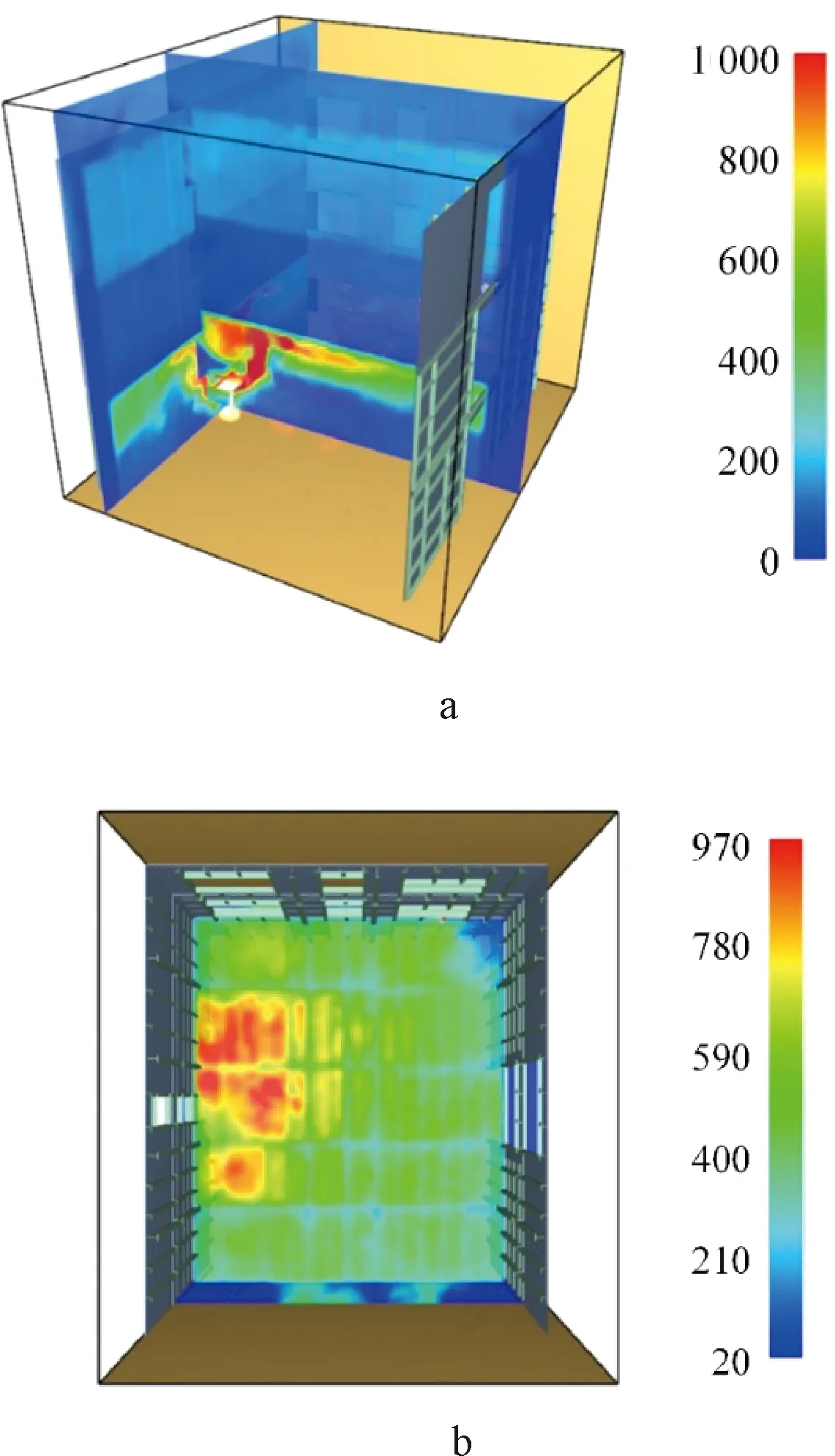
a—竖直方向; b—水平方向(Z=2.9 m)。图12 火灾场景5温度场分布 ℃Fig.12 Temperature fields in different directions in scenario 5

a—竖直方向; b—水平方向(Z=5.8 m)。图13 火灾场景6温度场分布 ℃Fig.13 Temperature fields in different directions in scenario 6

a—竖直方向; b—水平方向(Z=5.8 m)。图14 火灾场景7温度场分布 ℃Fig.14 Temperature fields in different directions in scenario 7

2.2.2测点-温度时间曲线

火灾场景4和5的火源分别位于一层的E区和D区,火灾场景6和7的火源分别位于二层的E区和D区;4个火灾场景在不同高度处的时间-温度曲线见图15～18所示。

a—一层Z=1.5 m; b—一层Z=2.9 m; c—二层Z=4.4 m、 Z=5.8 m; d—三层Z=7.3 m、Z=8.7 m。图15 火灾场景4各测点温度-时间曲线Fig.15 Temperature-time curves of measurement points in scenario 4

a—一层Z=1.5 m; b—一层Z=2.9 m; c—二层Z=4.4 m、 Z=5.8 m; d—三层Z=7.3 m、Z=8.7 m。图16 火灾场景5各测点温度-时间曲线Fig.16 Temperature-time curves of measurement points in scenario 5

a—二层Z=4.4 m; b—二层Z=5.8 m; c—一层Z=2.9 m与三层Z=7.3 m、Z=8.7 m。图17 火灾场景6各测点温度-时间曲线Fig.17 Temperature-time curves of measurement points in scenario 6

a—二层Z=4.4 m; b—二层Z=5.8 m; c—一层Z=2.9 m与三层Z=7.3 m、Z=8.7 m。图18 火灾场景7各测点温度-时间曲线Fig.18 Temperature-time curves of measurement points in scenario 7

由于火源位置的不同,场景4和6高温所对应的区域为E区,场景5和7对应的为D区。4个场景最高温度都达到了1 000 ℃以上。

场景4和5的最高温度出现在一层火源所在E区和D区处,Z=1.5 m处最高温度在1 000 ℃左右,一层屋顶因为热空气上升的原因,场景4的E区和场景5的D区温度也稳定在了900 ℃以上;火源外的其他分区在Z=1.5 m处的温度集中在100～200 ℃,Z=2.9 m屋顶则呈现不同分区间的温度差异较大,场景4有D、F和C区在500 ℃以上,其余则在400 ℃以下,场景5温度较高分区为A区和E区,其余在400 ℃以下;对比图15c、d与图16c、d可知:场景4二层和三层的整体温度要高于场景5,但最终顶层楼板温度都在100 ℃左右。

场景6和7的最高温度出现在二层火源所在分区E区和D区上方,场景6在Z=4.4 m处最高温度在1 100 ℃,场景7则达到了1 200 ℃,二层屋顶Z=5.8 m的D、E区后续也稳定在了1 000 ℃左右;火源外的其他分区在Z=4.4 m处的温度集中在200 ℃以下,Z=5.8 m屋顶处不同分区间的温度差异较大,场景6有F和G区在500 ℃,其余分区则在300～400 ℃,场景5温度较高分区为A区和E区,其余在400 ℃以下;对比图17c与图18c可知,一层温度几乎不变,维持在20 ℃,场景6三层的整体温度要稍高于场景7,最终顶层楼板温度都在100 ℃左右。

由4种场景下的时间-温度曲线可知:火源所在楼层的层中高度处,火源所在分区升温速度极快,时间-温度曲线斜率近乎呈垂直趋势,温度极高,均在1 000 ℃以上,其余分区则温度较低,在200 ℃以下,且呈现相似的变化趋势;火源所在楼层屋顶高度处的温度比起层中高度处的温度变化较为缓和,并且温度稍低于层中高度处的温度,而其余分区则远高于层中高度处的温度,且距火源越近的分区温度越高;4个场景中第三层的温度变化较为一致,由于楼梯口位于C区,上下层的空气流通、传热都须要通过此处,所以C区空气温度较高,在300～400 ℃,顶层温度则都在100 ℃。从各层温度-时间曲线可见:位置越高的测点,曲率越缓和,体现了屋顶热空气慢慢积聚的过程。

3 结构温度场计算及分析

3.1 单层结构

由于火源位置不同,对应的室内空气温度场分布也不尽相同,从而影响空气与结构之间的热对流,对结构传热升温造成极大影响。以下为3种不同工况下的单元传热过程,火灾发展过程中的时刻用T表示。

3.1.1火灾场景1

当T=1 631 s时,中心E区楼板升温至400 ℃以上,钢材材性已经开始微变;T=5 531 s时,B、C区升温缓慢,D、H两分区楼板升温最快,已达400 ℃以上,火源所在的E区位置楼板温度已经达到900 ℃,其余分区楼板温度均在300 ℃左右,整体结构墙板也在逐渐升温;T=7 231 s时,E区楼板温度有所回落,降至868 ℃,除B、C区楼板温度在300 ℃外,其余分区楼板温度均在400 ℃,Z≥1 m的墙板温度已达300 ℃以上;T=9 981 s时,整体结构温度场已经稳定,如图19所示。

a—T=1 631 s; b—T=5 531s; c—T=7 231s; d—T=9 981 s。图19 火灾场景1不同时刻温度场 ℃Fig.19 Temperature fields at different points in time in scenario 1

3.1.2火灾场景2

当T=300 s时,D区楼板升温至450 ℃,靠D区近的窗口上缘也升温迅速,升温至200 ℃以上,其他位置温度均处于200 ℃以下;T=388 s时,D区楼板升温至600 ℃,钢材进入屈服状态,窗口上缘钢板温度升至300 ℃以上,其余位置温度均在200 ℃以下;T=1 122 s时,D区楼板温度升至822 ℃,A、E、G区楼板温度在488 ℃,窗口周边结构温度在600 ℃左右,靠近火源的上半部分墙板在300 ℃左右;T=2 022 s时,结构温度场基本稳定,如图20所示,D区楼板温度在900 ℃左右,A、E、G区楼板温度在500 ℃左右,洞口附近墙板温度在800 ℃左右,西侧其余墙板温度在400 ℃左右。

a—T=300 s; b—T=388 s; c—T=1 122 s; d—T=2 022 s。图20 火灾场景2不同时刻温度场 ℃Fig.20 Temperature fields at different points in time in scenario 2

3.1.3火灾场景3

当T=478 s时,A区楼板温度达416 ℃,近火源的西侧墙板温度升至300 ℃,D、E区楼板比其余分区楼板升温快,已达200 ℃左右;T=628 s时,A区楼板温度已升至600 ℃左右,北侧近火处窗口上方墙板温度升至500 ℃左右,西侧墙板温度上升至400 ℃左右,D、E区楼板温度在250 ℃左右;T=808 s时,A区楼板温度升至700 ℃,北侧近火处窗口上方墙板温度为600 ℃左右,西侧墙板温度在500 ℃左右,D、E区楼板温度在300 ℃左右;T=1 077 s时,结构温度场已基本稳定,如图21所示,A区楼板稳定在800 ℃,北侧近火处窗口墙板温度达到了800 ℃,火源附近的B、D、E区楼板温度也达到500 ℃以上,西侧墙板温度在600 ℃左右。

a—T=478 s; b—T=628 s; c—T=808 s; d—T=1 077 s。图21 火灾场景3不同时刻温度场 ℃Fig.21 Temperature fields at different points in time in scenario 3

3.2 三层结构

由空气温度场计算结果可知,三层结构与单层结构有很大不同,以下为4种不同工况下最终稳定后的整体结构和各楼层的结构温度场分布。

3.2.1火灾场景4

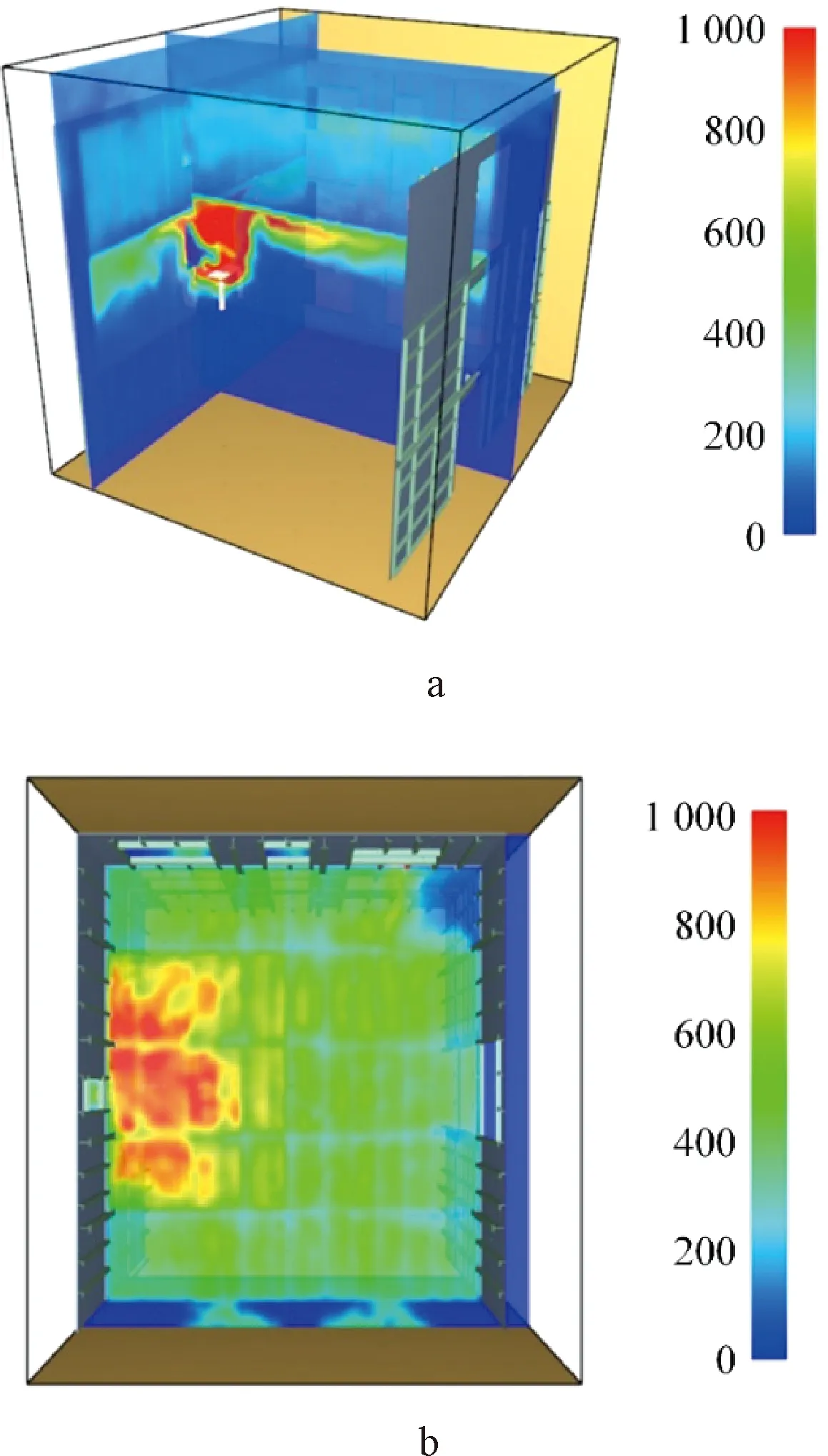
当T=6 027 s时,整体结构温度已经接近稳定,温度场分布如图22a所示。由于火源位于一层中心位置,所以在三层整体结构温度场模型中一层楼板及墙板的温度都较高,而二、三层温度分布不明显。单独截取一～三层的结构温度场分布如图22b～d所示,可见:一层楼板火源上方楼板达到了960 ℃,楼板其余位置温度则在400～500 ℃,中部以上的墙板温度大约在330 ℃;二层所有分区中C区温度较高,墙板底部温度达到250 ℃,墙板上部和楼板的温度都在180 ℃,这是因为一层层顶C区布置有楼梯口,热空气会通过该洞口流通,造成局域温度较高,其他区域的楼板和墙板中上部均温也在100 ℃;三层楼板比二层楼板温度略有上升,均温110 ℃,C区墙板温度在200 ℃以上,其他墙板均温在160 ℃,该层呈现了温度随高度升高而降低的规律。

a—整体结构温度场; b—一层结构温度场; c—二层结构温度场; d—三层结构温度场。图22 火灾场景4不同楼层结构温度场 ℃Fig.22 Temperature fields on different floors in scenario 4

3.2.2火灾场景5

当T=7 017 s时,整体结构温度已经接近稳定,如图23a所示。各层结构温度场分布如图23b～d所示。可知:首层楼板火源处D区温度最高,达到944 ℃,D区的墙板温度在550～700 ℃,其他位置处的楼板和墙板均温在300～400 ℃;二层稳定后最高温度位于C区,墙板底层温度在200 ℃左右,中间高度处温度约240 ℃,楼板温度在140 ℃左右,其余分区楼板和墙板均为80 ℃左右;三层C区墙板底层温度在130 ℃左右,中间高度处温度约200 ℃,其余位置处墙板均温约为130 ℃,而顶层楼板温度整体较为平均,大约为100 ℃。

3.2.3火灾场景6

当T=6 642 s时,整体结构温度已经接近稳定,结构温度场分布如图24a所示。各层结构温度场的分布如图24b～d所示。可知:首层结构整体温度较低,均温20 ℃,只有墙板顶和C区附近区域温度稍高,在25 ℃左右;二层楼板E区最高温度达954 ℃,其他分区楼板温度在500 ℃左右,墙板除C区外,中部以上部分温度都在400 ℃,而C区因为楼板洞口的存在,火源所在楼层产生的热空气向上流动被带走,所以还保持着较低的温度;三层也呈现随高度升高温度逐渐降低的趋势,顶层楼板均温在130 ℃,大部分墙板则维持在200 ℃左右。

a—整体结构温度场; b—一层结构温度场; c—二层结构温度场; d—三层结构温度场。图24 火灾场景6不同楼层结构温度场 ℃Fig.24 Temperature fields on different floors in scenario 6

3.2.4火灾场景7

当T=7 472 s时,整体结构温度场已经接近稳定,如图25a所示。各层结构的温度场分布如图25b～d所示。可知:首层结构整体温度较低,均温为20 ℃,只有墙板顶部和C区附近温度稍高,25 ℃左右;二层D区楼板最高温度达996 ℃,A、E区楼板温度在550 ℃左右,F区楼板在400 ℃左右,D区墙板温度也较高,在500～900 ℃,靠近楼板洞口的C区依旧温度较低,在20 ℃左右,其他分区墙板和楼板均温约350 ℃;三层楼板均温约为100 ℃,C区墙板温度在210 ℃左右,其余墙板均温约为170 ℃。

a—整体结构温度场; b—一层结构温度场; c—二层结构温度场; d—三层结构温度场。图25 火灾场景7不同楼层结构温度场 ℃Fig.25 Temperature fields on different floors in scenario 7

4 结束语

以一个模块单元组成的单层箱板结构和三个模块单元组成的三层箱板整体结构为研究对象,通过数值模拟方法得到了箱板钢结构空气温度场及结构传热规律:

1)针对箱板结构内部空气温度场,火源所在区域不同高度的时间-温度曲线有很大差异,越靠近火源的测点,初始升温速率越大,且升温速率随时间逐渐增大,曲线斜率最大时接近竖直状态,与ISO国际升温曲线相比,室内最高温度要大于ISO曲线温度,比起室内采用统一升温曲线的传统计算方法,根据高度分区计算更符合实际情况;

2)由7种火灾场景下的时间-温度曲线计算结果显示,单层结构同一高度处,火源所在位置区域温度最高,3种工况下最高温度都达到900 ℃以上,其他区域则离火源越近温度越高,并且出现温度随高度升高而升高的趋势;三层结构火源所在楼层温度最高,4种工况下最高温度达1 000 ℃以上,层内离火源越近的区域温度越高,底层楼层温度基本不变,均温在20 ℃,顶层楼层的空间的时间-温度曲线较为缓和,层内温度分布均匀同时温度也较低,都在100 ℃左右,并且出现温度随高度升高而降低的趋势;各曲线曲率随高度升高逐渐缓和,体现了屋顶热空气缓慢积聚的过程;

3)由火灾瞬态热分析计算得到的结构温度场显示,单层箱板结构火源上方楼板温度最高,3种工况下最高温度都在800 ℃以上,墙板底部温度最低,均温在20 ℃左右;三层箱板结构在4种工况下最高温度都在900 ℃以上,位于火源上方楼板处,火源位置楼层墙板温度随高度升高而升高;当火源位于一层时,一层整体平均温度较高,二层整体平均温度为200 ℃,三层整体均温为100 ℃,当火源位于二层时,二层整体平均温度较高,一层整体温度维持在20 ℃,三层平均温度为150 ℃,火源外的其他楼层温度较低且分布更均匀;

4)箱板装配式钢结构室内空气温度场具有明显的分层性和区域性,空气温度场与结构温度场分布总体呈现一致趋势,火源所在楼层的温度随空间高度升高而升高,而由于楼层之间的密闭性和热空气的向上流动,底部楼层温度基本不变,上部楼层温度会较低且分布更均匀。