海洋环境施工钢栈桥腐蚀特征研究及稳定承载力分析*

2023-05-25程为

工业建筑 2023年2期

程为

(中铁建大桥工程局集团第四工程有限公司, 哈尔滨 150000)

跨海桥梁桥址区存在水深、浪高、流急等特点,且波浪荷载对跨海桥梁设计和施工的影响很大[1-3]。平潭海峡公铁两用大桥位于福建省平潭县,施工区域温度高、湿气重、海水含盐度较高,施工钢栈桥极易出现严重的腐蚀现象,同时该区域海水的水流、波浪作用大,为钢栈桥临时结构的安全带来较大隐患[4-6]。

近年来,有较多学者对沿海地区钢栈桥的腐蚀问题进行了调查,如大连港鲇鱼湾、甘井子、寺儿沟等港区多座钢栈桥[7-10],其基础部分为钢筋沉箱墩台,上部为钢结构,钢桥面板距离水面1～4 m,表面均涂有防腐漆,但目前部分桥面板及焊接部位防腐漆出现了开裂、脱落等现象;大连北大桥[11]钢结构桥建成已17年,施工时防腐技术比较落后,目前该桥桁架、桥塔、工作平台均已严重腐蚀;武汉琴台文化艺术中心[12]钢栈桥采用热浸镀锌防腐措施,但由于长期处于潮湿环境下,结构交接部位出现局部锈蚀现象,部分防腐漆已剥落。

虽然目前已有较多有关钢栈桥腐蚀的研究,但与钢栈桥受力性能有关的文献仍较少,而钢管桩腐蚀后稳定性能的研究更是稀缺,因此腐蚀环境下钢管桩的竖向承载问题有待进一步研究。本文基于福平铁路平潭海峡公铁两用大桥钢栈桥,对其深水裸岩区钢栈桥的腐蚀现状展开研究:对腐蚀钢材进行现场取样,对钢构件表面腐蚀形态进行测定;对腐蚀钢管桩进行力学模型简化,基于理论推导确定腐蚀后钢管桩的相对计算高度;采用ABAQUS软件建立腐蚀后钢管桩的精细化有限元模型,对腐蚀后钢管桩轴压稳定承载力进行分析,为未来钢栈桥施工提供参考。

1 工程概况

1.1 钢栈桥概况

平潭海峡公铁两用大桥位于福建省平潭县,全长约16.34 km,桥位区全年6级以上大风天气超过300 d,年均发生3.8次台风,多年风力均速可达6.9 m/s,100年重现期浪高9.69 m。桥址处风急浪高,海洋环境极其恶劣。为提高海上作业工效,减少船机设备使用,大桥基础采用长栈桥辅助施工平台施工方案。钢栈桥跨度最大28 m,采用(8+28/24) m的孔跨布置,4根钢管桩横向和纵向布置均为8 m,栈桥示意如图1所示。钢管桩选用φ1 800×20、φ1 420×16管桩,材质为Q235B,其元素成分见表1。栈桥施工区域最深水深达45 m,其中水深18～45 m区域的栈桥占栈桥全长的55%,栈桥已经服役5年。为此,本文主要以深水区跨度为28 m处的钢管桩为研究对象。钢栈桥下部结构的防腐措施参考JTS 153-3—2007《海港工程钢结构防腐蚀技术规范》[13],防腐涂层种类及厚度如表2所示。

表1 Q235B钢板元素成分及含量Table 1 Elemental composition and content of Q235B steel plate %

表2 钢栈桥下部结构防腐涂层种类及厚度Table 2 Types and thicknesses of anti-corrosion measures for steel trestles μm

1.2 腐蚀环境概况

平潭地区处于亚热带气候带、东亚季风区,温热湿润,具有典型的季风性气候,海域属于半日潮类型。该地区全年平均温度高于20 ℃,平均降水量高于1 300 mm,海水含盐量的年平均值为3.0%～3.2%,最高达3.6%。以上数据说明,平潭海峡公铁两用大桥所在区域温度高、湿气重,且海水含盐度较高。钢栈桥常年处于上述严酷的海洋环境中,必然会发生严重的腐蚀破坏。现有研究表明,钢结构腐蚀层中主要成分为α-FeOOH、β-FeOOH、γ-FeOOH及Fe3O4等,腐蚀产物呈疏松、多孔的状态,不能对内部未腐蚀钢材形成保护层;同时部分氧化产物(β-FeOOH)的存在加速了钢材的腐蚀速率,导致钢材在海洋环境中出现更严重的腐蚀问题[14-16]。钢材受腐蚀后不仅导致构件截面受损,还对钢材的强度、延性等力学性能产生影响,导致构件的承载力有所降低,为钢栈桥临时结构的安全带来较大隐患。此外,该地区大风天气多,有效作业时间较短,且钢栈桥临时结构搭建长度较长、施工环境复杂,钢材进入施工场地后未能及时开展作业即已出现腐蚀现象,造成了钢材极大的浪费。

2 钢材腐蚀形态测定

对钢管桩表面腐蚀形态进行测定,能最直观地反映出钢材的腐蚀状况,从而鉴定工程结构是否存在安全隐患。

2.1 腐蚀钢材现场取样

根据现场腐蚀情况排查,钢管桩表面防腐层部分脱落,可观察到大量蚀坑,选取其中腐蚀最为严重的钢管桩进行现场取样。由于钢管桩所处腐蚀区域较广,下部处于腐蚀的全浸区,中部属于浪溅区和潮差区,上部处于大气区,因此需要分别对4个不同区域的钢材进行取样以分析不同腐蚀区域对钢材腐蚀性能的影响。不同腐蚀区域钢管桩表面取样钢板的平面尺寸为150 mm×150 mm。

钢管桩长期处于富含电解质海水中,钢管表面在氧气、阳光、潮湿海风和浪花飞溅等因素共同作用下容易发生电化学腐蚀。以铁的氧化物为主的腐蚀产物附着在钢管桩表面,导致微观测量难以进行,因此需要对腐蚀钢材表面进行酸洗除锈。本文严格按照ASTM标准[13]要求配制酸洗溶液,采用刷子进行反复刷涂酸洗至完全除去铁锈。

2.2 腐蚀形态测定

采用光学数码显微镜对酸洗后的试件进行超景深试验,对腐蚀后钢材的微观形貌进行分析。在光学数码显微镜中,可以观察到腐蚀后试件表面的蚀坑形状。根据不同的蚀坑深度,对不同深度的蚀坑采用不同的颜色进行划分,可以得到超景深试验彩图,如图2所示。可以看出,不同腐蚀区域内取样钢材的腐蚀程度差异明显。

a—浪溅区; b—全浸区; c—潮差区; d—大气区。图2 扫描后试件表面形貌示意 μmFig.2 Schematic diagrams of specimen surface state by scanning

基于超景深试验结果可知:钢管桩呈现非均匀腐蚀状态,浪溅区钢材点腐蚀最为严重,其腐蚀深度远大于其他区域,浪溅区点腐蚀最大腐蚀深度可达到0.446 mm,全浸区最大腐蚀深度为0.087 mm,潮差区为0.433 mm,大气区为0.248 mm。即浪溅区的最大腐蚀深度是全浸区的5倍,这是由于浪溅区同时接触海水与空气,加上海浪冲击、干湿交替、温度变化等因素的叠加作用导致此处腐蚀最为严重。

为了量化点腐蚀的影响,通过概率统计的方法确定腐蚀钢材表面蚀坑的分布规律。分别汇总统计每个腐蚀区域钢材腐蚀深度,得到钢材腐蚀深度的频数分布直方图,如图3所示,其中横坐标为钢材腐蚀深度d与最大腐蚀深度dmax之比,纵坐标为相对频率。由图3可知,全浸区、潮差区和大气区钢材腐蚀深度分布均呈现两端低而中间高的正态分布,而浪溅区钢材腐蚀深度分布呈现逐渐上升的指数分布。

a—浪溅区; b—全浸区; c—潮差区; d—大气区。图3 钢材腐蚀深度的频数分布直方图Fig.3 Frequency distribution histograms of steel corrosion depths

以腐蚀深度之比d/dmax为自变量,相对频率为因变量,对数据进行拟合分析,建立腐蚀深度分布概率函数。文献[17]提出可以采用回归判定系数(R2)评价模型的可靠性,而且当R2≥0.95、0.80≤R2<0.95、0.65≤R2<0.80和R2<0.65时,其预测结果的精度分别为“优”“良”“中”“差”。可以发现,浪溅区、全浸区、潮差区和大气区钢材腐蚀深度分布概率函数相对应的判定系数(R2)分别为0.945、0.941、0.886和0.871,可见,本文提出的腐蚀深度分布概率函数可以较好地预测不同腐蚀区域内钢材的腐蚀分布规律。

基于腐蚀深度分布概率函数,可以计算得出不同区域钢材点腐蚀的腐蚀速率:全浸区、浪溅区、潮差区和大气区钢材点腐蚀的腐蚀速率分别为0.011,0.076,0.034,0.027 mm/a。

3 腐蚀钢管桩受力模型的简化

海洋环境下钢材的腐蚀导致钢管桩承载力降低,加剧了构件整体失稳的可能,然而现行规范并未给出考虑腐蚀损伤影响的构件承载力设计方法。因此,基于不同腐蚀区域钢材的超景深试验结果,本文将此类构件简化为由若干个均匀壁厚柱段组成的阶梯柱,并建立简化力学模型,对其进行屈曲分析。

3.1 等截面轴心受压柱端约束之间的相互关系

图4为上端可移动的等截面轴心受压柱,两端受抗弯弹簧约束。柱的上端具有滑动弹簧铰,下端具有固定弹簧铰,约束常数为r1和r2,分别表示柱上端和柱下端有单位转角时的约束弯矩。

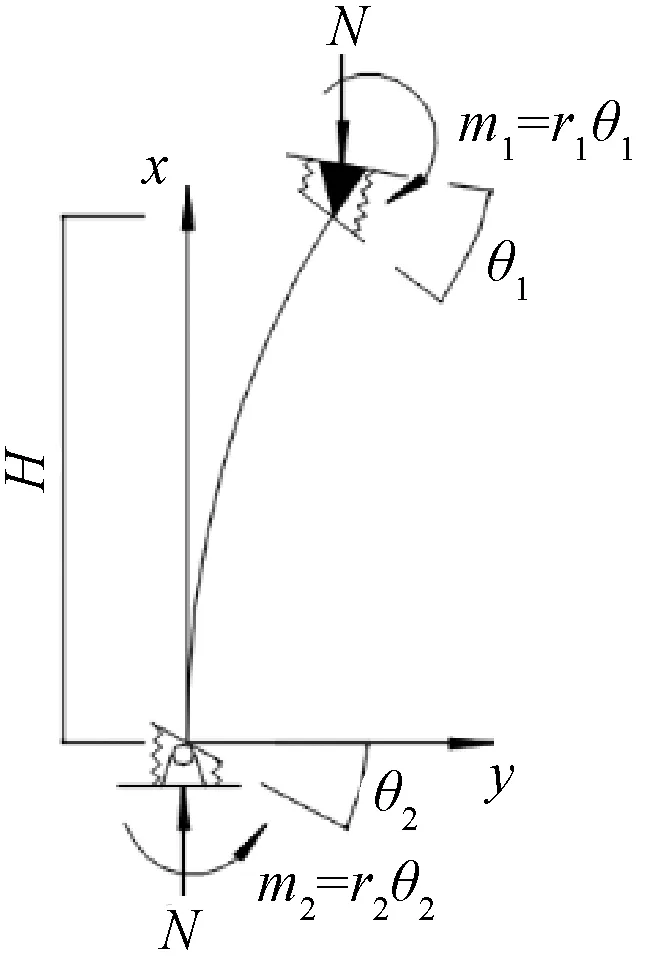
图4 有侧移柱柱端转角与弯矩示意Fig.4 The schematic diagram of rotation and bending moment of column end with lateral deflection

建立柱任意截面的弯矩平衡方程,对原点取矩:

Ny(x)-M(x)-r2θ2=0

(1)

基于此,可得到有侧移柱柱端约束常数r1和r2之间的关系式:

(2)

式中:μ为计算长度系数;E为弹性模量;I为截面惯性矩。

3.2 有侧移的轴心受压单阶柱约束常数

基于等截面轴心受压柱的分析原理,对柱截面变化的单阶柱进行分析。将两柱段划分为图5b和图5c两个隔离体,分别进行计算,上、下端部及柱段连接处抗弯刚度分别为r0、r2和r1。图5a的轴心力作用下在柱顶有某一转角θ0时所应施加的力矩m0=r0θ0,图5b上端和图5c下端具有连续性,变形和内力协调。

基于等截面轴心受压柱端约束之间的相互关系可知,有侧移的轴心受压单阶柱约束常数r0的表达式为:

a—单阶柱; b—下柱段; c—上柱段。图5 两柱段计算简图Fig.5 Calculation model of two-segment stepped columns

(3)

式中:μi、Hi、Ii分别为上、下柱段的计算长度系数、柱高与截面惯性矩,其中,i=1,2。

3.3 变截面柱计算长度系数

当柱上端为自由端,端部没有约束弯矩,柱端能自由转动的同时还能侧移,失稳时柱上端的弯矩m0=r0θ0=0。因为θ0≠0,只有r0=0,则式(3)变为:

(4)

上下段柱的线刚度比值:

(5)

临界力参数:

(6)

上、下段柱的临界力分别为:

N1=π2EI1/(μ1H1)2

(7a)

N2=π2EI2/(μ2H2)2

(7b)

最终可得单阶柱计算长度系数:

(8)

求解上式即可得到柱上端为自由的单阶柱下段柱的计算长度系数μ2,而上段柱的计算长度系数μ1=μ2/η1。

3.4 变阶柱计算长度

由于钢管桩随着暴露条件的不同沿高度可划分为全浸区、潮差区、浪溅区和大气区,因此可以将腐蚀后的钢管桩简化为三阶柱力学模型。三阶柱计算长度系数在GB 50017—2017《钢结构设计标准》[18]中尚无表可查,因此本文基于单阶柱计算长度系数的推导方法提出了三阶柱计算长度系数的公式。

将四段柱划分为图6a和图6b两个隔离体,分别进行计算。假定上段柱、中段柱和下段柱的临界力分别为:

Ni=π2EIi/(μiHi)2

i=1,2,3,4 (9)

式中:μ1,μ2,μ3,μ4分别为各段柱的计算长度系数。轴心作用下钢管桩临界力均相等,故有:

N1=N2=N3=N4

(10)

上段柱与下段柱线刚度比值、中1段柱与下段柱线刚度比值、中2段柱与下段柱线刚度比值分别为:

a—有限元模型; b—三阶柱; c—上柱段。图6 四段柱有限元模型及计算简图Fig.6 Calculation model of four-segment stepped columns

(11a)

(11b)

(11c)

临界力参数:

(12a)

(12b)

(12c)

可得三阶柱计算长度系数计算公式:

(13)

采用数值计算方法通过MATLAB编程对三阶柱计算长度系数计算式(式(13))进行求解,即可得到柱上端为自由的三阶柱下段柱的计算长度系数μ4,而上段柱、中段柱1、2的计算长度系数μ1、μ2、μ3通过μ4计算可得:μ1=μ4/η1,μ2=μ4/η2,μ3=μ4/η3。

为保证理论推导的正确性,选取特殊工况对计算长度系数公式进行验证。选取工况为三阶柱各阶截面均相等,即三阶柱为等截面柱。对于等截面柱,当柱上端为自由端、下端固定时,长度计算系数为2.0。相同工况下,采用式(13)对三阶柱计算长度系数进行求解,可得μ1=μ2=μ3=μ4=2.0,由此可以证明计算长度系数公式的正确性。

基于得到的计算长度系数,可以提出三阶柱的相对计算高度公式为:

Heff=μ1H1=μ2H2=μ3H3=μ4H4

(14)

式中:Heff为相对计算高度。

3.5 理论结果与有限元结果的对比分析

本文采用ABAQUS软件建立钢管桩的有限元模型对理论推导公式展开验证。选取C3D8R实体单元模拟钢管,建立4个等截面部件模拟组成四段柱的4个柱段,不同柱段的壁厚不同,各部件之间通过TIE连接。根据施工栈桥实际情况,将钢管桩边界条件简化为底端固接、顶端自由。荷载作用方式为轴压荷载,通过Buckle分析可得到腐蚀后钢管桩的屈曲临界力,模型如图6a所示。钢材本构采用双折线模型,应力-应变关系见式(15),其中,fy为钢材屈服强度,εy为屈服应变,Es为弹性模量,取2.06×105MPa,泊松比取0.3。为方便讨论,定义Ki为各柱段与下柱段线刚度的比值,并在工程实际应用范围内(0.2～5.0)选取Ki。

(15)

对比阶梯柱屈曲临界力的理论计算结果(Ncr,Cal)与有限元分析结果(Ncr,FE)如图7所示,其中,Ncr,Cal通过式(16)计算得到。可知,Ki在0.2～5.0范围内时,Ncr,Cal和Ncr,FE的结果十分接近,拟合后直线斜率为0.998 5,接近1.0,由此可以说明本文提出的相对计算高度公式是合理的。

(16)

图7 临界力计算结果对比Fig.7 Comparison between calculated and finite element results of critical load

4 钢管桩稳定承载力计算

考虑到腐蚀后钢管桩在几何缺陷、加载偏心和残余应力等复杂因素影响下承载力无法达到屈曲临界力,本节将采用三种方法(理论计算法、精细化有限元模型以及均匀腐蚀简化有限元模型)对腐蚀后钢管桩的实际稳定承载力展开分析。以深水区28 m跨度处施工钢栈桥腐蚀后的钢管桩为例,其中,柱高H=46 m,直径D=1.8 m,初始壁厚t0=20 mm。浪溅区、全浸区、潮差区和大气区高度分别为13.8,18.4,4.6,9.2 m。

1)理论计算时,将腐蚀后钢管桩简化为三阶柱模型,各柱段壁厚均匀减少,腐蚀厚度按等效损失质量法考虑,具体如式(17)所示。

(17)

式中:m0和m分别为腐蚀前、后钢管的质量;d为等效均匀腐蚀深度。

在该条件下,浪溅区、全浸区、潮差区和大气区的腐蚀厚度分别为0.357,0.035,0.260,0.124 mm。在底端固接、顶端自由的工况下,将上述参数代入式(13)可解出全浸区柱段计算长度系数μ4= 5.06,计算长度L0=μ4H4= 93.11 m,由此可知长细比λ= 147.40。查询GB 50017—2017可以得到稳定系数φ=0.356,则稳定承载力计算值Nu,cal=φAfy= 9 356.59 kN。

2)为验证理论计算结果的准确性,本文考虑腐蚀后钢管的表面形貌,采用ABAQUS建立了腐蚀后钢管单桩的精细化有限元模型并进行稳定承载力计算。采用C3D8R实体单元模拟腐蚀前钢管,并基于超景深试验结果在钢管表面不同腐蚀区域内生成相应数量的蚀坑,其后通过切割操作实现钢管的腐蚀损伤,如图8所示,其中红色点状区域表示蚀坑。钢管桩的几何参数按实际工况取值,钢材本构与其余各参数取值与3.5节保持一致,初始缺陷取一阶屈曲模态,幅值为H/1 000,通过弧长法可得到腐蚀钢管桩的稳定承载力Nu,FE1= 9 796.43 kN。

3)建立精细化有限元模型需要明晰钢管的表面形貌,建模过程繁琐,不便于实际应用。因此本文提出采用3.5节中的简化阶梯柱有限元模型计算腐蚀后钢管桩的稳定承载力,即将腐蚀后钢管桩按腐蚀区域分成4个柱段,假设各柱段产生腐蚀均匀,腐蚀深度按式(17)取值,与理论计算中的腐蚀深度保持一致。通过弧长法计算得到的腐蚀钢管桩稳定承载力Nu,FE2= 9 823.30 kN。