基于混合整数线性规划模型的SPONGENT S盒紧凑约束分析

石一鹏，刘 杰*，祖锦源，张 涛，张国群

（1.西北工业大学 软件学院，西安 710129；2.上海机电工程研究所，上海 201109）

0 引言

SPONGENT［1-2］是一种基于海绵结构的轻量级哈希函数，它的作用是针对可变长度有限位的输入，通过吸收、压缩等步骤输出一个固定位数的哈希值。在SPONGENT 中，使用了类 似PRESENT［3］的基于代换-置换网 络（Substitution-Permutation Network，SPN）结构的轮函数，该轮函数的输入是经过有限步简单处理的原始输入信息，输出是最终生成的哈希值。因此，轮函数是SPONGENT 中生成哈希值的关键结构，对SPONGENT 的差分密码分析，最重要的就是针对轮函数分析差分密码。

差分密码分析是针对现代分组密码最有效、最著名的攻击方法之一，目前已经应用到很多密码的攻击中，因此抵抗差分攻击的能力也逐渐成为评估加密算法安全性能的基本要求。Ankele 等［4］针对Sparx-64/128 分析了15 和16 轮的差分特征；ElSheikh 等［5］针对CRAFT 算法分析了差分密码；Ji等［6］针对GIFT-64 和GIFT-128 展开了密钥相关的差分路径搜索；杨继林等［7］针对类CLEFIA 动态密码结构分析了差分特征。

同时，很多基于差分密码分析的新的密码分析方法也逐渐诞生，并广泛应用于多种密码算法的安全性分析中，如Wei 等［8］对TWINE 算法展 开了不 可能差 分密码分析；Moghaddam 等［9］对Midori、SKINNY 和CRAFT 算法展开了截断差分分析；Hutahaean 等［10］对小型PRESENT 算法展开了飞去来器分析（boomerang attack）；陈少真等［11］对GOST2 算法展开了密钥相关攻击等。

差分密码分析的基本思想是通过研究密码输入差分和输出差分之间的关系猜测密钥，为了提高攻击成功的概率，需要寻找一条高概率的差分路径；然而密码在经过数轮迭代之后产生的差分可能十分复杂，分析处理时可能面临十分庞大的数据量。

Mouha 等［12］提出将混合整数线性规划（Mixed Integer Linear Programming，MILP）模型应用于差分路径的自动搜索，为寻找高概率的差分路径提供了一种全新的思路，通过这种方法可以有效地找到活动S 盒数量的下限。但最初提出的模型忽略了S 盒自身的差分特性，不能够用于面向位进行处理的加密算法，如PRESENT［3］、LS-Design（Linear-Sbox-Design）［13］、GIFT［14］等。Sun 等［15］使用描述S 盒可能和不可能差分模式的方法，将Mouha 等［12］提出的模型扩展到了面向位的密码算法的差分分析中；但是该S 盒描述方法不能保证得出描述S 盒的最优方式。Sasaki 等［16］在文献［15］的基础上改进了MILP 模型，提出了一种新的约简算法，获得了理论上的最优描述，大幅提高了差分路径搜索的效率。此后MILP 模型在差分密码分析中有了更多的应用。如，Zhu 等［17］基于MILP 模型对GIFT-64 展开了12 轮差分特征的研究；Bagherzadeh 等［18］基于MILP 模型对LEA 和HIGHT 分析了差分密码；Kumar 等［19］基于MILP 模型对WARP 分析了18 轮和19 轮的差分特征。

基于以上的分析，针对SPONGENT 的轮函数应用MILP模型进行差分路径搜索时，可以较好地解决SPONGENT 差分路径搜索效率低下的问题。由此，将SPONGENT 差分路径搜索问题转变为针对它的轮函数进行MILP 建模的问题；而对于具有典型SPN 结构的轮函数，建立MILP 模型，最重要的步骤就是寻找S 盒的最优描述。所谓“最优”，就是在不违背S盒所规定差分模式的条件下最大限度地减少冗余不等式的数量，即寻找一种“紧凑约束”。本文基于约简算法［16］分析了SPONGENT 的S 盒的紧凑约束。此外，无法忽略一个事实——即使约简算法［16］在应用过程中展现了很好的实际效果，但是目前仍没有一种严谨的方法证明所得到约束结果的紧凑性。因此，本文提出了一种可能的方法，从约束条件存在必要性的角度验证所得到约束的紧凑性。

本文的主要工作为：

1）使用不等式对SPONGENT 中S 盒所有差分模式的最小凸集描述，得到287 个不等式，应用约简算法［16］在287 个不等式中筛选，首次得到了一组由23 个不等式组成的约束。

2）提出了一种评价约束条件必要程度的指标，并给出了基于该指标的约束紧凑性验证算法，用于对所得到的不等式约束验证紧凑性。针对所得到的SPONGENT S 盒的约束应用该算法，结果表明，所得到的约束中，每一个不等式都是不可替代的，即23 个不等式组成的约束对于SPONGENT 的S 盒是紧凑的。

1 SPONGENT

1.1 SPONGENT的版本参数

SPONGENT 是一个基于海绵结构的哈希函数家族，根据不同的散列输出值的位数（size）、capacity和rate，SPONGENT可以被分为13 个版本，不同的版本对应不同的加密轮数和安全等级。表1 以SPONGENT-size/capacity/rate的参数化形式标识不同的版本，并给出了每一个版本对应的和运算轮数（round）。其中：state是参与SPN 结构轮函数运算部分的位数；rate是state中参与异或运算的位数，也是输入信息分块处理的单位；capacity是state中不参与异或运算部分的位数，3 个参数满足state=rate+capacity。

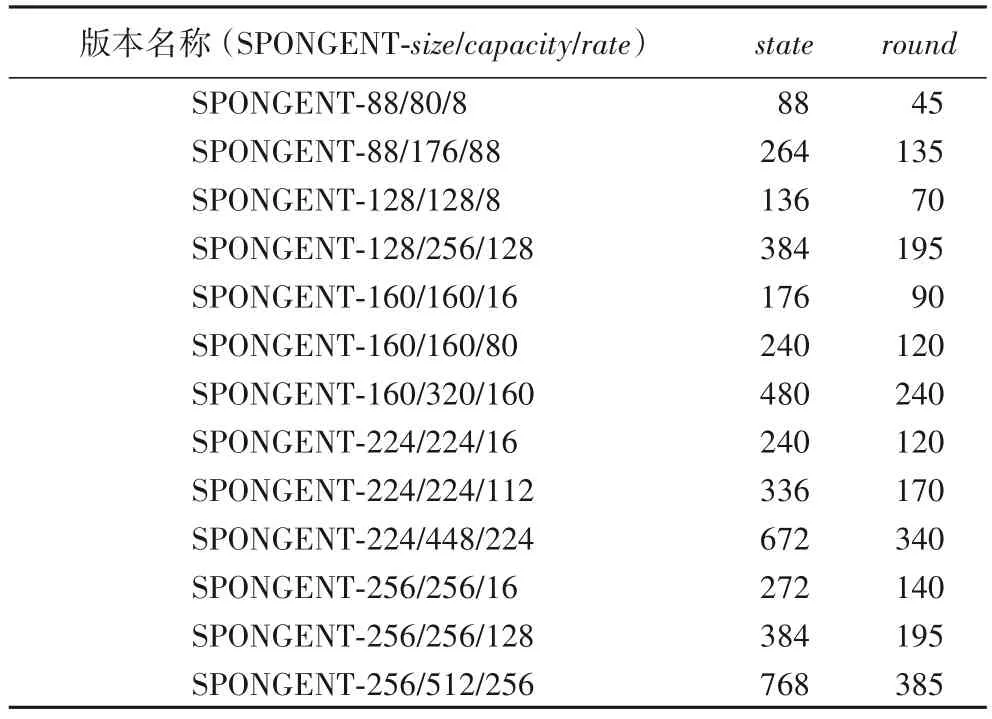
表1 SPONGENT版本参数Tab.1 SPONGENT version parameters

由表1 可知，SPONGENT 共有5 种长度的散列值输出，由SPONGENT-size表 示，分别为SPONGENT-88、SPONGENT-128、SPONGENT-160、SPONGENT-224 和SPONGENT-256。

1.2 SONGENT的计算过程

对于输入的消息，SPONGENT 进行以下3 个阶段的操作计算输出：

1）初始化阶段：将输入信息的位数扩展成为rate的整数倍，再将它分割为若干个rate位的分块。

2）吸收阶段：将初始化阶段得到的若干个分块逐步与state的前rate位异或运算。

3）压缩阶段：通过SPN 结构的轮函数逐步计算得到输出值。

1.3 SONGENT中的轮函数

在SPONGENT 所用的轮函数中主要进行以下运算：

1）state与轮常数及其反序值进行异或运算，根据state的位数不同，轮常数相应的初值不同。

2）state通过S 盒完成字节代换，每一次代换的字节由4位组成，使用b表示state的位数，每一轮需要进行b/4 个平行运算。表2 为S 盒规格的16 进制表示，x经过代换变为S(x)。

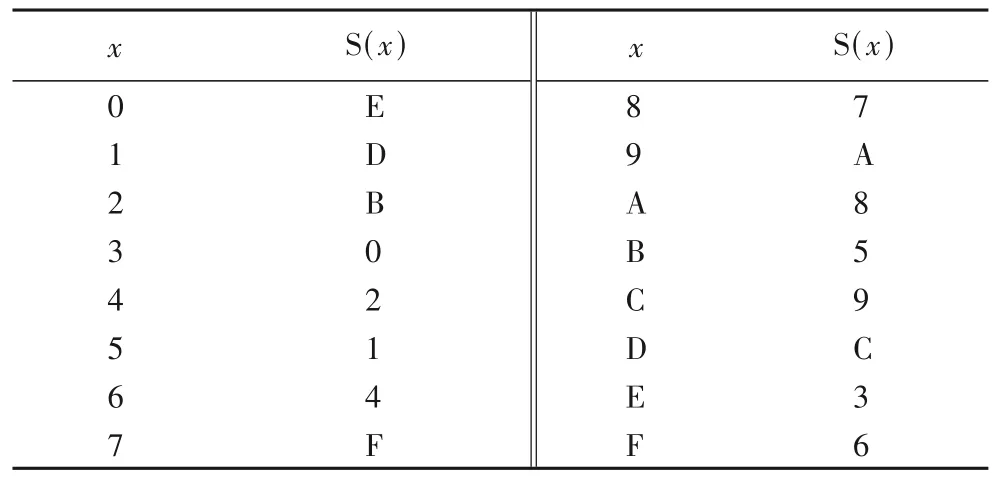
表2 S盒规格的16进制表示Tab.2 Hexadecimal representation of S-box specification

3）state进行P 盒置换运算，这里的P 盒与PRESENT 所用P 盒的置换规则类似，都是一种宽轨迹策略的运算。第i位的值被置换到第P（i）位，运算规则为：

本文重点分析S 盒的紧凑约束，对于轮函数的运算过程不作更多讨论。在得到S 盒的紧凑约束之后可以针对轮函数的结构建立更加高效的MILP 模型，从而进行更高效的差分密码分析。

2 MILP在最优差分路径搜索中的应用

MILP 应用于差分路径搜索之前，已经在很多领域发挥过重要的作用，它的含义可分为“混合整数”以及“线性规划”两部分。“线性规划”即表明这是一种使用变量约束和不等式约束对目标函数优化的数学方法；“混合整数”则强调其中的一些变量被限制为整数值，而其他变量可以是二进制值或连续值。对于最优差分路径的搜索，可以使用相应的变量约束和不等式约束描述可能的差分路径，并将差分路径的概率作为目标函数，该MILP 模型的解即对应最优的差分路径。

2.1 文献［12］分析框架

Mouha 等［12］提出将MILP 应用到差分路径分析时，给出了针对SPN 结构3 种常见操作的不等式分析。

2.1.1 异或操作不等式分析

使用Xin1、Xin2表示异或运算的输入差分，Xout表示相应的输出差分，3 个参数之间的关系可以表示为：

其中⊕表示异或运算。可以发现，当且仅当Xin1与Xin2值都为0 时，Xout的值为0，否则3 个参数之间至少有两个值不为0。使用一个虚拟变量d∈{0，1}辅助表示这种关系：

2.1.2 线性操作不等式分析

使用w(x)表示一个向量x的汉明重量，差分分支数BD满足以下公式：

2.1.3 S盒操作不等式分析

对于双射的S 盒，当且仅当输入差分为0 时，输出差分也为0。即满足以下公式：

2.2 收紧MILP可行域的方法

利用文献［12］的方法针对SPN 加密结构建立MILP 模型之后，就可以针对不等式约束求解，最优的差分路径就是不等式解空间中的一个解。

然而，针对面向位的密码算法，在庞大的解空间中寻找最优的差分路径并不比应用MILP 之前更容易；并且，在这个解空间中很多差分路径是不可能出现的。因此需要寻找到一种收紧MILP 可行域的方法，尽可能多地剔除不可能出现的差分路径，以缩小最优差分路径的搜索范围。

通过添加不等式约束条件排除不可能的差分模式，就可以有效排除很多不可能差分路径，这样的不等式约束被称为截断不等式。

Sun 等［15］提出了两种生成截断不等式的方法：针对统计规律逻辑建模，以及差分模式最小凸集的H-表示。由于受到统计规律的限制，针对统计规律逻辑建模的方式并不适用于大多数加密结构，因此以下主要介绍差分模式最小凸集的H-表示。

定义1将S 盒所有可能的差分模式描述为一个离散点集，这个点集的最小凸集可以表示为若干不等式的公共解，那么称这一组不等式为S 盒所有可能差分模式最小凸集的H-表示。

例如，S 盒的输入差分为x=1001 时，可能的输出差分为y=1001 或y=1100，输入差分为x=1011 时，可能的输出差分为y=1011 或y=1110。使用（x3，x2，x1，x0，y3，y2，y1，y0）表示一个差分模式，那么所有可能的差分模式组成的点集为｛（1，0，0，1，1，0，0，1），（1，0，0，1，1，1，0，0），（1，0，1，1，1，0，1，1），（1，0，1，1，1，1，1，0）｝，最小凸集的H-表示为：

S 盒所有可能差分模式最小凸集的H-表示中含有大量有效的截断不等式。

2.3 获取紧凑约束的方法

随着可能差分模式的增多，最小凸集H-表示的不等式会越来越多，例如PRESENT 中S 盒所有可能差分模式最小凸集的H-表示为327 个不等式。这样庞大的不等式组合极其冗杂，导致MILP 在有限时间内难以完成求解。然而，由于不可能的差分模式是有限的，排除所有不可能的差分模式并不需要如此多的不等式，只需要选择可以排除所有不可能差分模式的截断不等式组合就可以达到收紧可行域的目的。因此可以在不影响原有约束有效性的同时尽可能地减少不等式的数量，以便不等式求解，即所谓得到紧凑约束的过程。

为了尽可能地减少不等式数量，Sun 等［15］利用贪心算法的思想筛选不等式：依次选择可以排除更多不可能差分模式的不等式，直到所有的不可能差分都被所选择的截断不等式排除。

使用该贪心算法可以得到一个较优解，但无法保证所得到的不等式数量是最少的；并且对于可以排除相等数量不可能差分模式的截断不等式，并没有明确给出选择的优先级。基于这种情况，Sasaki 等［16］提出了一种新的约简算法，应用MILP 选择最优不等式组合，它的基本步骤为：首先计算每个不可能的差分模式可以被哪些不等式排除，得到一个关于不可能差分模式和截断不等式之间的指导二维表，如表3 所示，单元值为1 表示它对应的不可能差分模式可以被对应的截断不等式排除；然后设定约束条件为每一个不可能差分模式至少被一个不等式所排除，同时设定每一个不等式最多可以选择一次；最后设定目标函数为最少的不等式数量，进行MILP 求解。

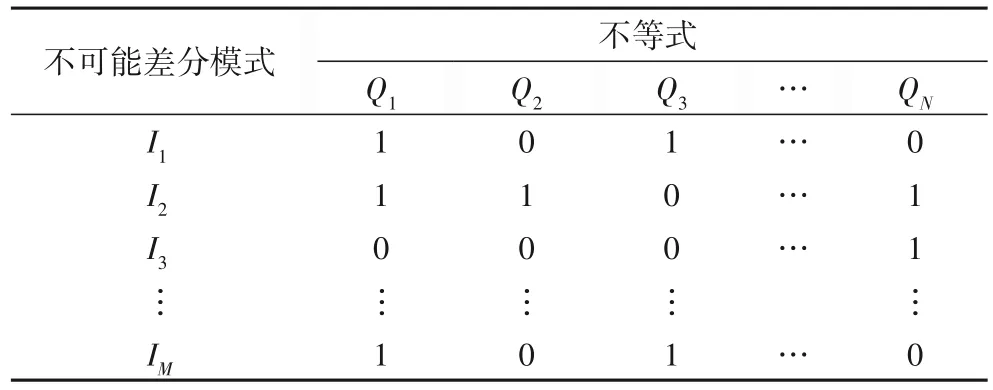
表3 指导二维表样例Tab.3 Example of 2D guidance table

3 SPONGENT S盒的约束分析

为了寻找S 盒的紧凑约束，本章使用Sasaki 等［16］提出的约简算法展开具体分析，主要步骤包括：计算所有可能的差分模式、求解截断不等式和缩减不等式数量。

3.1 计算所有可能的差分模式

求解SPONGENT 中S 盒所有可能的差分模式，得到输入-输出差分表，如表4 所示。

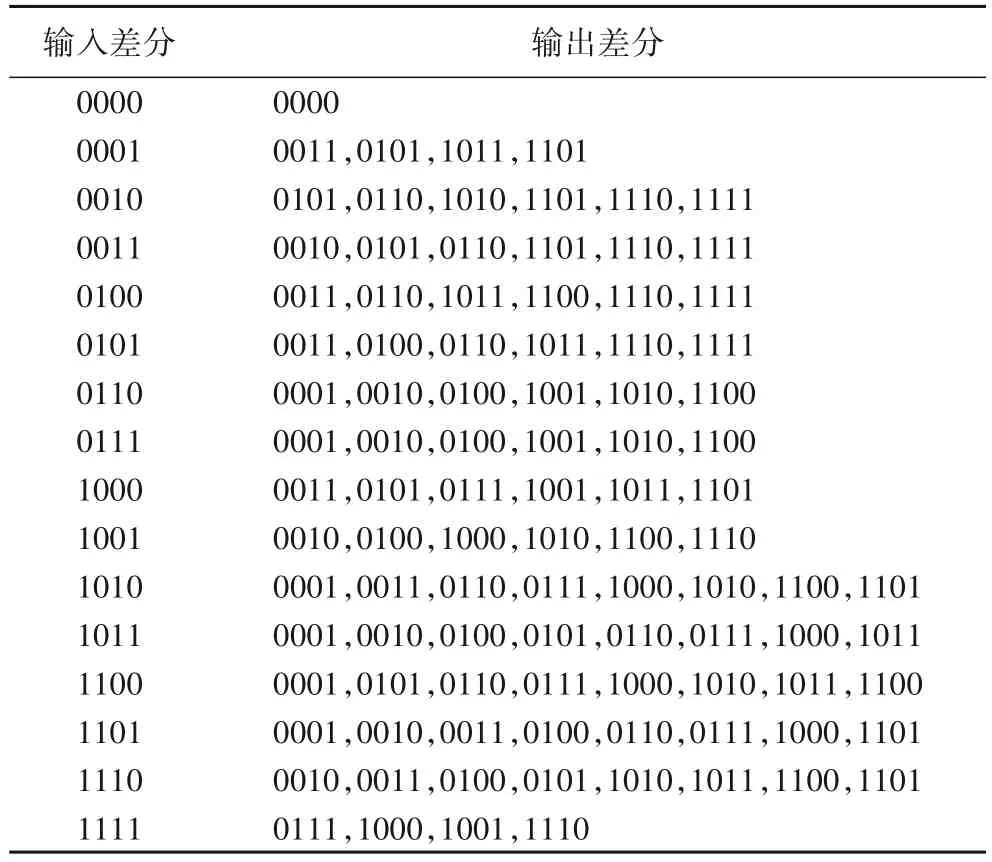
表4 输入-输出差分表Tab.4 Input-output difference table

例如，输入差分x=0001 时，可能的差分输出有：y=0011，y=0101，y=1011，y=1101，则可能的差分模式包括（0，0，0，1，0，0，1，1），（0，0，0，1，0，1，0，1），（0，0，0，1，1，0，1，1），（0，0，0，1，1，1，0，1）。

3.2 求解截断不等式

根据表4 可以得到97 个可能的差分模式，对应97 个点，使用SageMath 中的函数inequality_generator（）计算得到它的凸集的H-表示，共含有287 个不等式：

对所有的不等式按照顺序从0 开始编号，以便下一步计算，最后一个不等式的编号为286。使用变量Ij∈{0，1}(j∈{0，1，…，286})表示每一个不等式。

3.3 缩减不等式数量

计算所有不可能的差分模式，共有256 -97=159 个，并对所有的不可能差分模式从0 开始编号，最后一个不可能差分模式编号为158。

然后应用约简算法［16］，得到了类似表3 的159×287 的二维表，如可以排除第20 个不可能差分模式（1，1，1，0，1，0，0，0）的不等式有I23，I28，I41，I193，I223和I242：

令Ij=1 表示选择保留这个不等式，Ij=0 表示不保留该不等式，则由第20 个不可能差分模式可以得到约束条件为：

对全部不可能差分模式进行以上步骤，可以得到关于Ij的159 个不等式约束，求解得

对应值为1 的不等式为：

上述不等式组即为所求S 盒的约束。

4 紧凑性验证

4.1 紧凑性验证算法

4.1.1 约束不等式集合的紧凑性

在S 盒所有可能差分模式最小凸集的H-表示中，每一个截断不等式可以排除的不可能差分模式会有重合的部分，如表3 中，不等式1 和3 都能排除不可能差分模式1，不等式1、2和N都能排除不可能差分模式2。这种重合的情况在最终所求得的不等式约束集合中同样存在，而这恰恰是发现不等式约束集合可能存在冗余的一个重要突破口。

为了更好地表示这种冗余的情况，本文使用一个具体的案例说明。如表5 所示，使用Qi表示待选择的截断不等式，使用Ij表示需要被排除的不可能差分模式，当单元格值为1时，表示它对应的不可能差分模式可以被对应的截断不等式排除，表5 中Q1到Q8所能排除的不等式数量为降序排列。

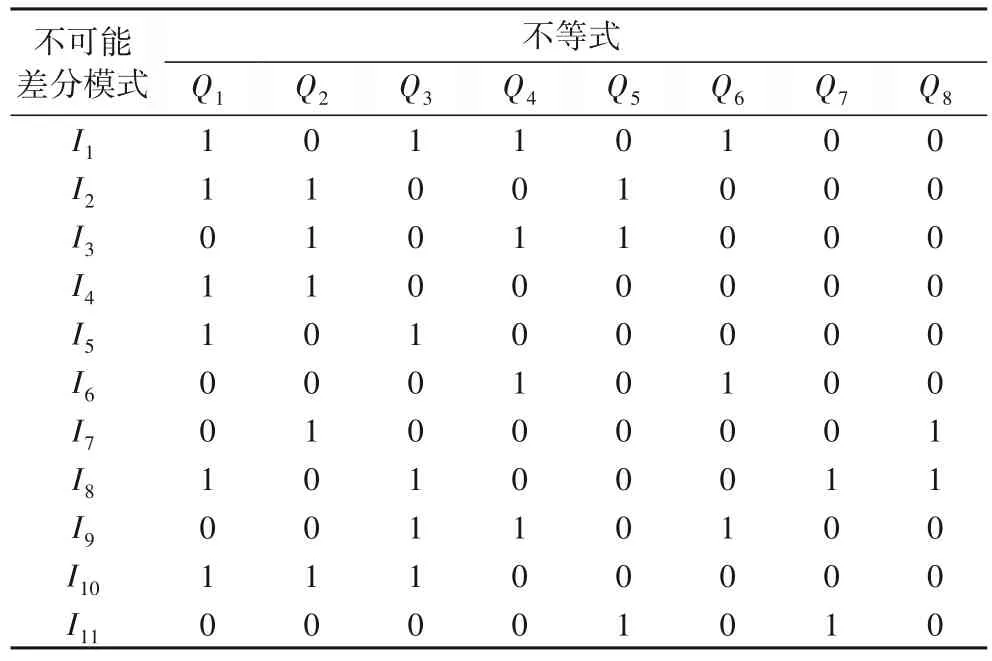
表5 冗余不等式约束案例Tab.5 Case of redundant inequality constraints

针对表5 中的数据应用贪心算法［15］筛选不等式，依次选取可以排除不可能差分模式最多的截断不等式，直到所有的不可能差分模式都被排除，得到的筛选结果为Q1、Q2、Q3、Q4、Q5。不难发现，Q1排除的不可能差分模式都可以被Q2、Q3、Q4、Q5组成的其他不等式组排除，不等式Q1对整个不等式约束集合就是冗余的。删去Q1对于不等式约束集合排除不可能差分模式的能力没有任何影响，但是却可以减轻运算的负担，提高差分路径搜索的效率。

使用MILP 模型进行S 盒约束不等式求解的目标，是希望使用尽可能少的不等式描述S 盒所容许的差分模式，并且排除所有不可能的差分模式。由于求解关注的重点之一是不等式的数量，因此一切可能导致不等式约束集合存在冗余的情况都应当被排除，这对于差分路径搜索复杂度的提升具有重要的意义。无论使用哪一种算法求解不等式约束集合，都应当保证最终的求解结果自身是紧凑的。为此，需要针对不等式约束集合验证紧凑性。

遗憾的是，目前尚未有一种方法能够针对不等式约束集合的紧凑性验证，为此，本文提出一种可行的方法。

4.1.2 紧凑性验证算法

为了验证不等式约束集合的紧凑性，本文首先定义了一个评价约束条件必要程度的指标“必要度”，使用参数Necessity∈{0，1，…}表示，定义如下：

定义2对于一个约束条件，在整个约束条件集合中由该条件唯一排除的不可能差分模式的数量定义为该约束条件的必要度。

当一个不等式的必要度为0 时，表示该不等式对于约束组合是非必要存在的。此时，原不等式约束集合就是不紧凑的，一个紧凑的不等式约束集合至少不能包含该不等式。

基于约束不等式的必要度，本文提出了一种验证约束条件集合紧凑性的算法，如算法1 所示。

算法1 验证约束条件集合紧凑性的算法。

4.1.3 算法的正确性及应用

算法1 是基于“必要度”的概念设计的。对于一个不等式约束集合，算法1 能够计算每一个不等式的必要度，当不等式约束集合中存在必要度为0 的不等式时，则判定该不等式约束集合是不紧凑的；反之，若所有不等式的必要度都不为0，则判定该不等式约束集合是紧凑的。

由于“必要度”代表一个不等式能够唯一排除的不可能差分模式的数量，当不等式约束集合中存在必要度为0 的不等式时，表明该不等式所排除的每一个不可能差分模式都能被其他不等式所排除，去除这个不等式对于不等式约束集合整体排除不可能差分模式的能力没有影响，因此当前的不等式约束集合存在冗余不等式，是不紧凑的；同样，若每一个不等式的必要度都非0，则表明每一个不等式都至少有一个不可能差分模式是其他所有的不等式都不能排除的，若去除其中某个不等式，新的不等式约束集合就无法排除对应的不可能差分模式，因此当前不等式约束中的每一个不等式都有存在的必要，当前的不等式约束集合是紧凑的。由此可以证明，算法1 能够准确判定一个不等式约束集合的紧凑性。

对于表5 中所示案例，使用Sun 等的贪心算法［15］得到的约束不等式集合与使用本文算法1 优化得到的约束不等式集合如表6 所示。

表6 不等式约束集合的优化结果Tab.6 Optimization results of inequality constraint set

使用贪心算法［15］得到的约束不等式集合为｛Q1，Q2，Q3，Q4，Q5｝。使用算法1 得到其中各个不等式的必要度分别为：0、1、0、1、1。此时可以得知，Q1和Q3对于不等式约束集合而言是冗余的。去除Q1，得到新的不等式约束为Q2、Q3、Q4、Q5，此时各个不等式的必要度分别为2、2、1、1，即新的不等式约束集合是紧凑的。由此可知，算法1 对于鉴别约束不等式集合的紧凑性以及指导约束集合优化具有实际的有效性。

值得注意的是，对于一个不等式约束集合而言，其中各个不等式的必要度会相互影响，去除或替换某一个不等式，其他不等式的必要度很可能也会发生变化。如表6 所示，去除Q1之后，Q3的必要度由0 变化为2，这启示研究者在不等式集合中发现多个必要度为0 的不等式时，不可以直接将它们全部去除，而是应该每去除一个不等式重新评估一次必要度，采用回溯的方式找到去除不等式最多的方案。

表6 的案例说明，算法1 对于约束不等式可能存在的冗余情况具有很好的鉴别作用，对于不等式约束的改进和优化也具有很好的指导意义。对于应用Sun 等［15］提出的贪心算法进行差分分析相关研究遇到的问题［18］，或许可以使用算法1 解决；而对于Sasaki 等［16］改进之后的约简算法而言，使用算法1 可以验证其所得到结果的正确性。

由于Sasaki 等［16］的约简算法是基于线性规划的，并且以不等式数量的最小值作为规划目标，其所得的不等式约束集合中每一个不等式的必要度一定不为0。假设存在一个必要度为0 的不等式，它一定会在线性规划过程中因为“不等式数量最小化”这个优化目标而被排除，否则可以判定算法的实现过程出现了错误。

综上，算法1 对于Sun 等［15］提出的贪心算法具有很好的优化效果，当出现必要度为0 的不等式时，可以根据算法1 指导不等式约束集合的优化；对于Sasaki 等［16］改进之后的约简算法则具有很好的检验作用，当出现必要度为0 的不等式时，证明算法的实现过程存在错误，从而及时矫正。

4.1.4 算法的时间复杂度

对于拥有m个不等式、n个不可能差分模式的不等式约束，使用验证算法紧凑性验证，首先需要计算每一个不等式的必要度，这一过程的时间复杂度为O（mn）；之后需要检查是否存在必要度为0 的不等式，这一过程的最坏时间复杂度为O（m）。综上，本文验证算法的时间复杂度为O（mn）。

4.2 约束紧凑性验证

4.1节中说明，使用Sasaki 等［16］改进之后的约简算法得到的约束不等式集合应当是紧凑的，若得到的不等式集合不是紧凑的，则说明算法实现过程中出现了错误。因此针对3.3 节中得到的约束应用算法1，得到每一个不等式约束的必要度如表7 所示。由表7 可知，3.3 节中所得的每一个不等式约束必要度都不为0，即每一个不等式都有存在的必要性，算法实现过程是正确的，所得的约束不等式集合是SPONGENT S 盒的一个紧凑约束。

表7 不等式约束的必要度Tab.7 Necessities of inequality constraints

5 结语

随着MILP 在差分密码分析中的地位日渐升高，寻找建立高效不等式约束的方式也变得更加重要。本文使用MILP模型针对SPONGENT 中S 盒的紧凑约束展开了分析，得到了紧凑的23 个不等式约束；同时定义了评价约束条件必要程度的参数“必要度”，并在此基础上提出了一种约束紧凑性验证的算法。结果表明本文提出的基于MILP 的SPONGNET 的S 盒紧凑约束分析方法可实现高效、紧凑的差分路径自动搜索。未来的研究工作主要包括以下两个方面：基于本文所得到的S 盒紧凑约束，针对SPONGENT 的轮函数结构建立更加高效的MILP 模型，尝试对SPONGENT 的轮函数自动搜索差分路径，以求得到更好的分析结果；依据本文的分析方法，对其他密码算法进行紧凑约束分析，并利用本文的紧凑性验证算法验证所得到约束条件的紧凑性，建立SPONGENT 类加密算法的通用MILP 差分分析模型。