基于相似和差异双视角的高维数据属性约简

李元江，权金升，谭阳奕，杨 田

（智能计算与语言信息处理湖南省重点实验室（湖南师范大学），长沙 410081）

0 引言

随着数据规模的不断扩大，尤其是特征数量的急剧增长，维度灾难成为数据挖掘和人工智能的共性问题［1］。作为主要的数据压缩方法，属性约简能够根据某种评估规则筛选有效的特征，去除冗余特征，从而达到降维数据、简化计算、提高数据质量和模型泛化能力的目的［2］。

粗糙集［3］为属性约简提供了理论框架，在没有先验知识的情况下［4-6］，通过知识粒和近似算子计算上下逼近，筛选重要特征，进而制定推理规则。基于粗糙集理论，学者们设计了一系列属性约简算法［7-11］。其中，区分矩阵［12］是粗糙集理论中的一种属性约简方法，它关于特征的复杂度为线性级别，能够对高维数据进行快速降维［13］。

经典的区分矩阵模型聚焦于异类的样本，将能否区分异类的样本作为评估属性的标准，好的属性往往能够区分更多的异类样本对。但是在以往区分矩阵的研究中，没有基于同类样本对属性形成评价，导致同类样本的信息没有得到充分利用。针对这一问题，本文提出了异同矩阵，通过样本对相似性和差异性的两方面对属性形成综合评估，以充分利用原始数据表的信息，使属性约简结果更加合理可靠。

1 相关工作

维度灾难会降低机器学习模型的性能，导致学习算法失效，降维能将高维的原始数据转换为低维数据，同时尽可能保留数据的原始含义，从而使机器学习模型能够有效使用这些数据。

属性约简是降维中的重要方法，在粒计算领域，当前研究主要集中于粗糙集理论及其推广理论。由Pawlak［3］提出的粗糙集理论是重要的知识粒化模型。粗糙集以等价关系形成知识粒，通过上下逼近划分正域和边界，正域为能准确分类的样本的集合，基于正域的大小制定规则就能挑选出有效特征，这些规则包括依赖度［14-15］、信息熵［16-17］、相关族［18］、区分矩阵［12，19］等。这些方法在知识推理，机器学习，数据挖掘等邻域发挥着重要的作用［20-23］。

另外，有一些较新颖的属性约简思想被提出，包括：Armanfard 等［24］提出了一种局部特征选择的方法，区别于经典属性约简方法为所有样本生成一个约简子集，该方法为每个样本区域生成一个约简，从而对后续的学习更有针对性；Wang 等［25］提出了邻域自信息的概念，将粗糙集模型中的上近似纳入特征的衡量标准，能更加全面地考量特征子集；Zhu等［26］提出了一种多粒度的邻域粗糙集模型，在此基础上得到一种自适应特征选择方法；Yamada 等［27］针对高维生物数据提出了一种非线性特征选择方法；Hu 等［28］将属性的重叠度引入到k-最近邻粗糙集中，提高了约简数据的计算效率和分类性能。

以上方法都是基于不同的考量，形成新的属性约简的标准，但它们都面临共同的问题，即对于属性维度的时间复杂度或空间复杂度较高，算法效率较低。而区分矩阵算法对于属性维度的复杂度是线性级别的，因此能够处理更高维度的数据。

当前基于经典区分矩阵模型，结合其他模型，衍生出了一系列新的算法：Hu 等［14］用邻域关系替换等价关系，以样本为中心，固定半径形成邻域，进而形成上下逼近；Wang 等［29］在邻域关系的基础上进行改进，提出了邻域区分指数来衡量特征子集的区分能力。另一个方面研究则是对经典集合进行改变：Dubois 等［30］引入模糊集，形成了模糊粗糙集；Jensen等［31］首次把依赖度应用于模糊粗糙集，提出了新的属性约简算法；Chen 等［32］将区分矩阵的概念应用于模糊粗糙集中。

相较于原始模型，这些新的区分矩阵模型作出了基于邻域形成覆盖关系替代划分关系以及用模糊关系替代经典集合关系等改进，旨在更加充分地利用数据信息，其中覆盖关系能够处理连续数据，模糊关系生成的信息粒能包含更多信息。但经典区分矩阵及其衍生模型都没有完全充分利用样本信息，均只使用不同类别的样本信息对属性进行评价，并没有使用到大量的同类样本信息。

因此，为了更加充分地挖掘数据信息，异同矩阵的概念被提出。异同矩阵将同类样本相似度纳入对属性的衡量，形成同类相似度和异类差异度两个方面的评价。基于样本对在每个属性下的距离以及类别标签计算同类相似度和异类差异度，进而将所有样本对的信息形成异同矩阵，并提出相应的属性重要度对属性进行评价，通过启发式属性约简算法挑选出重要属性，去除冗余属性，完成属性约简。

2 基本概念

2.1 粗糙集

定义1［3］不可区分关系。设R是U上的一个等价关系，U/R表示R的所有等价类构成的集合，[x]R表示包含元素x∈U的R等价类。一个知识库就是一个关系系统K=(U，R)，其中U为非空有限集，称为论域，R是U上的一族等价关系。若P⊆R，且∩P也是一个等价关系，称为P上的不可区分（indiscernibility）关系，记为ind(P)。

定义2［3］上近似与下近似。给定知识库K=(U，R)，对于任意子集X⊆U和一个等价关系R∈ind(K)，则

基于依赖度和信息熵等方法的属性约简方法关于特征的复杂度高，难以处理高维数据。区分矩阵对于特征的复杂度较低，可快速约简高维数据。

2.2 区分矩阵

定义3［12］设I=(U，A，V，f)是一个知识表达系统，|U|=n，则I的区分矩阵为：

其中βij={a∈A|f(xi，a) ≠f(xj，a)}。

区分矩阵是一个n×n的对称矩阵，矩阵的每个元素记录了能够区分两个样本的属性集合。

定义3 中的区分矩阵存在两个问题：1）对于同类样本可能依然会进行区分，实际上与决策相关性更强的特征应该较少地区分同类样本对；2）在处理连续型数据时，将两个样本值是否相等作为区分标准太过严苛，相当于粒化水平太细，会导致模型出现过拟合的情况。

3 异同矩阵及属性约简

3.1 异同矩阵的基本概念

对于上述问题，文献［33］中提出了针对连续型数据的区分矩阵方法，将连续值的差值是否超过一个阈值作为区分标准，使第2）个问题得到了合理解决，但并没有解决第1）个问题。不考虑同类样本的情况，使这部分数据信息没有被利用，极有可能影响最终的分类效果。本文从样本对的相似性和差异性两方面对属性形成综合评估，提出异同矩阵以解决第1）个问题。

定义4异同矩阵。设I=(U，A，V，f)是一个知识表达系统，|U|=n，|A|=m，ak(xi)表示xi在属性ak下的属性值。则I的异同矩阵为：

其中：(xi，xj)为不同类别的样本差异度；Sak(xi，xj)为相同类别样本的同类相似度；|·|表示取绝对值；γ1、γ2分别为差异度和相似度阈值。

从定义4 可以看出异同矩阵是一个对称矩阵，因此计算矩阵时只需要计算一半即可。该异同矩阵的每个元素是一个1 ×m的列表，列表的每个数值相当于对属性进行评价，对于不同类别的样本，某属性下的样本值差距大于阈值，说明该属性能很好地区分它们，则记为1；否则不能区分，记为0。对于相同类别的样本，某属性下的样本值差距小于阈值，说明该属性不会错误地区分它们，因此记为1；否则记为0。

定理1对于定义4 中的异同矩阵，当同类相似度阈值取值为0，异类差异度阈值取值为0 时，异同矩阵变化为区分矩阵。

证 明 当γ1=0，γ2=0 时，对于任 意xi，xj，ak，如 果d(xi)=d(xj)，则(xi，xj)=0。如 果d(xi) ≠d(xj)，当ak(xi)=ak(xj) 时，(xi，xj)=0；当ak(xi) ≠ak(xj) 时，(xi，xj)=1。将定义4 中αij值为1 的位置对应的属性形成集合，即为定义3 中βij，此时，异同矩阵变换为区分矩阵。

根据定理1 可知，异同矩阵是对区分矩阵的推广，因此异同矩阵在优化区分矩阵的基础上保留了区分矩阵的良好性质。

基于异同矩阵，定义5 给出了属性重要度评估方法。

定义5属性重要度。设I=(U，A，V，f)是一个知识表达系统，|U|=n，|A|=m，ak(xi)表示xi在属性ak下的属性值。SDM为S的异同矩阵，则属性ak的属性重要度为：SIG(ak)=(ak)，其中αij(ak)表示αij的第k个值。

根据属性重要度，本文在3.2 节中设计了启发式属性约简算法。

3.2 基于异同矩阵的属性约简算法

基于异同矩阵的约简算法可以分为两步：第一步为建立异同矩阵，根据给定的阈值和定义4 遍历一半的样本对，建立异同矩阵；第二步为约简，根据第一步建立的异同矩阵，计算每个属性的属性重要度，选取属性重要度最大的特征ak进入约简，并将αij(ak)=1 的αij设置为(0，0，…，0)，每轮选择当前未被选择的属性直到所有αij都为(0，0，…，0)。对于算法的时间复杂度，假设样本数为n，特征数为m，算法的第一步要遍历一半的样本对，因此要进行(n(n-1))m次计算，时间复杂度为O(n2m)；第二步基于矩阵的运算复杂度是常数级别。因此，ARSDM 算法的时间度为O(n2m)。由于要基于每个属性存储样本对的信息，因此空间复杂度为O(mn2)。具体算法如下：

算法1 异同矩阵约简算法。

第一步：建立异同矩阵。

4 实验与结果分析

4.1 实验设置

实验数据集来自UCI 和scikit-feature 数据库，具体信息如表1 所示。对Fitting Fuzzy Rough Sets（FFRS）［34］、Granular Ball Neighborhood Rough Sets（GBNRS）［35］和Discernibility Matrix based on Graph theory（DMG）［36］三种属性约简算法进行对比，其中DMG 算法是区分矩阵算法的最新改进版本。对于属性约简结果，通过分类回归树（Classification And Regression Tree，CART）分类器和支持向量机（Support Vector Machine，SVM）分类器进行十折交叉验证，得到的结果为10次结果的平均值。

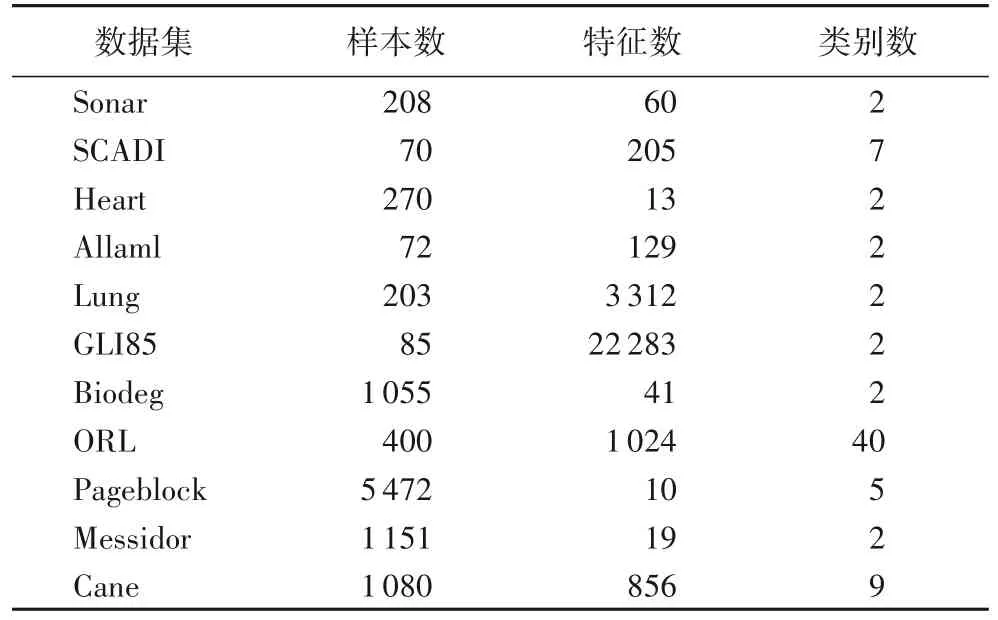
表1 数据集信息Tab.1 Dataset information

对于FFRS 和DMG，为了得到更好的结果，本文将δ设置为从0 到0.5 并以0.02 为步长进行遍历，因此会得到26 个结果，最终选取分类准确率最高的结果。GBNRS 算法运行不需要设置参数，但是GBNRS 的结果具有较大随机性，因此本文设置运行5 次，取最大准确率。同时，ARSDM 也对阈值γ1从0 到0.5 以0.02 为步长进行遍历，对阈值γ2=0.2γ1从0到0.1 以0.004 为步长进行遍历。ARSDM 也会得到26 个结果，选取分类准确率最高的结果作为最终约简。4 个对比算法的时间复杂度与空间复杂度如表2 所示。

表2 时间/空间复杂度对比Tab.2 Comparison of time/space complexity

本文实验均在同一环境下进行，使用Matlab R2018b 进行代码编写，在个人电脑上运行。个人电脑的系统为Windows 10，处理器是Intel Core i5-8250U CPU @ 1.60 GHz，内存是32.0 GB。

4.2 结果分析

原始数据（RAW）和4 个算法（DMG、FFRS、GBNRS 和ARSDM）在CART 和SVM 分类器上的约简数据的分类准确率分别如表3 和表4 所示，每个数据集的最大分类准确率用加粗字体表示。图1 和图2 分别展示了CART 和SVM 在不同数据集上的准确率变化。

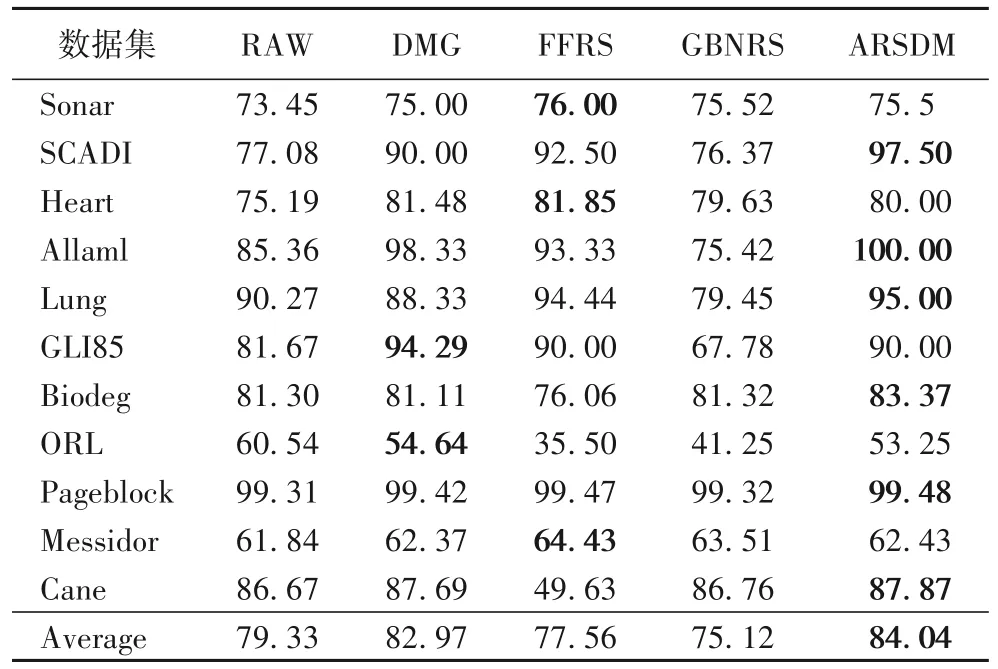
表3 CART分类器上约简数据的分类准确率比较 单位：%Tab.3 Comparison of classification accuracy on reduction data under CART classifier unit：%

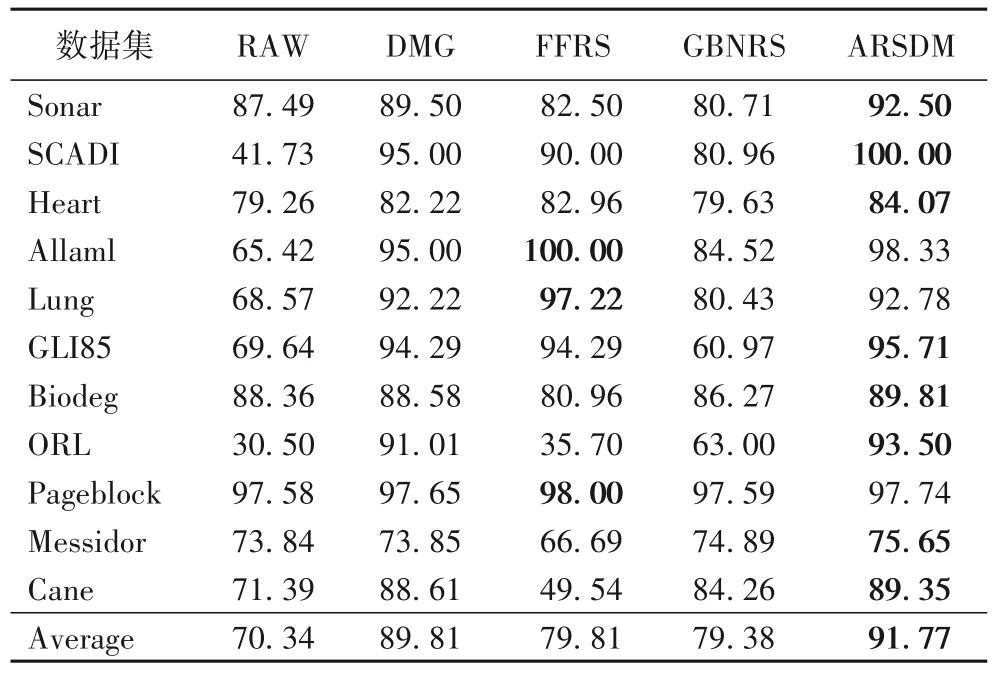
表4 SVM分类器下约简数据的分类准确率比较 单位：%Tab.4 Comparison of classification accuracy on reduction data under SVM classifier unit：%

表3、4 的结果表明，经过ARSDM 算法约简的数据分类准确率比原始数据高，说明ARSDM 在减小数据规模的同时，保证了约简数据的质量。对比另外三个算法的约简结果，在CART 分类器的评估下，ARSDM 对于数据集SCADI、Allaml、Lung、Biodeg、Pageblock、Cane 的分类准确率更高；在SVM 分类器的 评估下，对于数据集Sonar、SCADI、Heart、Lung、GLI85、Biodeg、ORL、Messidor、Cane 的分类 准确率更高。ARSDM 在两个分类器下的平均分类准确率均最高，其中，对比DMG、FFRS 以及GBNRS，在CART 分类器下的平均分类准确率分别提高1.07，6.48，8.92 个百分点；在SVM 分类器下的平均分类准确率分别提高1.96，11.96，12.39 个百分点。这说明对比只考虑样本差异度的DMG，加入样本相似度后的ARSDM 能够筛选出质量更高的属性进而提高分类准确率。而且对比经典的属性约简方法，ARSDM 对数据集的考察更全面，能够利用更多的信息，分类准确率较为稳定，有良好的鲁棒性。

表5 展示了4 个算法对不同数据集的约简时间，由于DMG、FFRS、ARSDM 需要针对26 个邻域参数计算26 次，以选择最好的结果，因此，约简时间是26 次计算的总时间。GBNRS 需要运行5 次选取最好结果，所以约简时间是5 次约简时间总和。从表5 中可以看出，对比DMG，ARSDM 平均运行时间更长，因为ARSDM 要额外计算样本相似度；对比FFRS 和GBNRS，ARSDM 平均运行时间更短；此外，对于高维数据，ARSDM 运行效率更有优势，例如GLI85；而对于样本数量大维度低的数据，ARSDM 运行效率较低，例如Pageblock。结合分类准确率结果，这说明ARSDM 更适合处理高维数据，能在对高维数据有效较低维度的同时保证较高效率。

表5 四个算法的约简时间对比 单位：sTable 5 Comparison of reduction time of four algorithms unit：s

5 结语

本文基于粗糙集理论对区分矩阵模型进行了优化，由于以往研究只考虑了不同类别的样本，形成的评价不够全面，因此，本文从相似和差异两个方面，加入了对同类样本相似性的衡量，提出了异同矩阵。在异同矩阵的基础上，提出了属性约简启发式算法ARSDM。在数值实验中，将ARSDM 算法与FFRS、DMG、GBNRS 约简结果对比，用CART 和SVM 分类器对结果进行评估。结果表明，ARSDM 能在原始数据上有效去除冗余属性，对比其他约简算法的结果，在多数数据集上分类准确率有明显提高。

ARSDM 算法在样本数量较多时的约简速度较慢。因此，后续的研究工作主要是两个方面：1）对ARSDM 算法进行优化，提高运行速度，处理维度更高的数据；2）将ARSDM 算法应用到增量学习中，使其能够处理动态数据。