基于协同变异与莱维飞行策略的教与学优化算法及其应用

高 昊，张庆科，卜降龙，李俊青，张化祥

（山东师范大学 信息科学与工程学院，济南 250358）

0 引言

近年来，随着待优化实际问题日益复杂，各种智能优化算法为代替传统优化方法而相继被提出，具有效率高、求解代价小的特点，以智能随机的方式求解，在计算精度、收敛速度、单目标与多目标问题、单峰与多峰等问题上各有侧重。教与学优化（Teaching-Learning-Based Optimization，TLBO）算法［1］是一种针对连续非线性大规模优化问题的优化算法，无需提前设定参数，不必关注参数对解质量的影响。目前，许多文献已将TLBO 算法及其相关变体应用于比例-积分-微分控制器（Proportion Integration Differentiation，PID）优化［2］、系统优化［3］、风险预测［4］、路径优化［5］、序列比对［6］、特征选择［7］、经济负荷调度［8］、故障检测［9］、图像工程［10］等领域，并取得了不错的应用效果。

与众多智能优化算法一样，TLBO 算法也会有陷入局部极值、算法早熟等问题。为了更好地解决这些问题，本文对TLBO 算法相关研究进展归纳总结如下：

1）种群初始化。Wang 等［11］使用Logistic 混沌映射初始化种群，生成均匀分布在解空间的个体，提升了种群多样性；Roy 等［12］提出一种基于反向学习的教与学优化（Oppositional TLBO，OTLBO）算法，使用反向学习生成反向种群，并在算法迭代过程中产生反向学习种群，与种群中相对应的个体进行比较，筛选比较好的个体来加快算法收敛速度。

2）引入策略和机制。Chen 等［13］提出了一种可变种群方案，种群规模随三角形震荡折线图的波动动态变化，在种群规模增长阶段使用高斯分布生成新个体，在种群规模减小阶段删除最相似的个体；Yu 等［14］提出了一种分组策略，将种群分为若干组进行老师的教学任务，防止算法过早收敛，同时在学生交流阶段让某位学生随机选择两名学生进行交流，以提升算法的种群多样性；Wang 等［15］让学习者在迭代学习过程中使用差异变异来保持学习者的多样性，避免了采用重复消除近似个体的重启方法造成算法时间复杂度的提升；Taheri 等［16］提出了一种平衡教与学优化（Balanced TLBO，BTLBO）算法，新增了辅导阶段与重启阶段，在提升算法局部勘探能力的同时又能兼顾全局探索能力；He 等［17］提出了一种混沌教与学优化（Chaotic TLBO，CTLBO）算法，将莱维飞行与混沌映射相结合，对适应度值较差个体执行莱维飞行策略，并对部分个体进行混沌搜索，提升了算法的全局搜索能力；Rao 等［18］提出了一种基于精英概念的精英教与学优化（Elitist TLBO，ETLBO）算法，使用精英解替换较差解，提升了种群整体质量；于坤杰等［19］提出了加入反馈学习阶段的反馈精英教与学优化（Feedback Elitist TLBO，FETLBO）算法，能平衡算法的全局探索与局部开发能力。

3）引入惯性权重因子。Niu 等［20］设计了一种随迭代次数线性递减的惯性权重，并用于教学阶段的个体更新，提高了算法的收敛速度；Wu 等［21］引入一种非线性惯性加权因子用于教学阶段和学习者阶段的学习者更新；Cao 等［22］设计了一种自适应权重因子来获得较强的全局搜索能力；Coelho等［23］提出一种基于混沌惯性权重的教与学优化（Chaotic Inertia Weight TLBO，TLBOCIW）算法，通过混沌权重更新个体，使个体在解空间中的分布更加均匀，种群的多样性得到提升。

4）混合算法。Zou 等［24］将粒子群优化算法（Particle Swarm Optimization，PSO）的社会特性融入TLBO 算法，个体位置的更新由原始位置、平均位置、全局最佳位置共同决定；Ouyang 等［25］在TLBO 算法中引入和声搜索（Harmony Search，HS）算法来优化当前最佳个体；Chen 等［26］在教学和学习者阶段加入模拟退火算子进行个体水平的更新。

由于不存在一种优化算法可以解决所有优化问题，针对算法的单一策略改进并不利于提升算法面对复杂问题的能力，因此，有必要进一步深入探究多策略融合方法。本文提出了一种基于均衡优化与莱维飞行策略的新型教与学优化（Equilibrium-Lévy-Mutation TLBO，ELMTLBO）算法，在解决算法易陷入局部最优、算法早熟等问题的同时，提升算法综合性能。首先，算法采用多精英均衡引导策略，避免种群陷入局部最优；其次，在莱维飞行的基础上引入一种自适应权重，二者结合平衡算法的局部勘探和全局探索能力；最后，设计包含多种变异算子的变异算子池，丰富了种群的多样性。

1 教与学优化算法

TLBO 算法主要灵感来源于课堂上学生学习进步的过程。在TLBO 中，一组学习者或一类学习者构成了整个种群，种群中的每一个个体通过成绩或水平来评价其优劣，种群的最佳个体被选择为老师，老师即为目前最佳解决方案，肩负着引领种群迭代的任务。基于以上描述，算法工作流程被分为两个阶段：教学阶段和学习者阶段。

1.1 教学阶段

在教学阶段，老师会根据学习者们的平均水平进行教学任务。教学阶段老师的教学过程描述如下：

其中：xmean为班级的平均水平，它是所有个体的算术平均值；i为个体编号，j为分量编号；nPop为种群规模，dim为个体维度；r1为［0，1］区间服从均匀分布的随机向量；TF∈{1，2}为教学因子，算法在TF=1 时偏向于全局搜索，TF=2 时偏向于局部搜索。

1.2 学习者阶段

在学习者阶段，一名学习者通过随机挑选另一名学习者进行相互交流学习。低水平者将向高水平者学习，而高水平者将吸取低水平者的经验教训。这个过程通过以下公式加以描述：

其中：k为与个体i交流的随机个体；r2为［0，1］区间服从均匀分布的随机向量。学习者通过上述两个阶段来提升自身水平，并选择种群中的最佳个体作为老师来引导种群进行下一次的迭代。

2 基于教与学优化算法的改进

2.1 均衡引导

均衡引导是一种避免全局最优解过度引导的策略。算法可以通过精英池筛选4 个精英解及1 个平均状态解作为引导个体，4 个精英解有助于提升算法的局部勘探能力，而作为4 个精英解算术平均值的平均状态解可以提升算法的全局探索能力。若候选解数少于4，会提高算法在单峰函数上的性能，但会降低算法在多峰和复合函数上的性能；若候选解数超过4 则会产生相反的效果［27］。在标准TLBO 算法中，老师作为种群的当前最佳决策方案引导种群进行迭代，若当前最佳个体陷入局部最优则导致整个种群更新停滞不前。于是，将均衡引导策略引入TLBO 算法是一种不错的解决方案。引导种群迭代的不再是当前迭代的最优个体，而是精英池中的精英，通过精英的均衡引导可以避免算法搜索停滞。

2.2 基于莱维飞行的自适应权重

莱维飞行可以在不确定环境中最大限度地提高资源搜索的效率，它常见于自然界中动物的觅食、移动等过程。莱维飞行服从莱维分布，它以极大的概率进行小范围游走，以极小概率产生一段长距离的飞行。这种随机游走属于一种马尔可夫链，即当前位置只与上一状态的位置及转移概率有关［28-29］。在此前的研究中，Yang［30］把莱维分布函数经过简化和傅里叶变换后得到它的幂次形式的概率密度函数如下：

生成一个服从莱维分布的随机数比较难，Yang［30］采用Mantegna 方法通过式（5）提取莱维飞行步长s：

其中：u～N(0，σ2)；v～N(0，1)；β=1.5。方差σ如式（6）所示：

其中：σ是通过复杂运算得到的一个标量；Γ 为伽马函数。

在调研国内外相关研究时，无一例外地发现很多有关于莱维飞行的改进算法均使用式（7）［31］进行个体更新。

其中：α为步长控制因子；⊗为点乘；Levy(β)为服从莱维分布的步长。

由于α的值会影响莱维飞行的方向及所产生的步长，因此本文在此前研究的基础上增大σ，减小出现远距离飞行的频率并增加莱维飞行所产生的步长，以平衡莱维飞行所提供的搜索能力。

如果莱维飞行产生的步长较大，会跳过全局最优解，而步长过小则会降低算法收敛速度，同时在算法陷入局部最优时也无法提供跳出局部最优的能力［32］。综上所述本文提出一种将莱维飞行与自适应动态权重相结合的方法，基于莱维飞行的权重来控制个体位置更新的过程，并提出如下公式：

其中：s是莱维飞行产生的步长；r3、r4和r5为［0，1］区间服从均匀分布的随机数；ub与lb分别为问题的上下界；RSR为缩放范围（Scaling Range，SR）因子，是根据问题上下界确定的步长缩量因子，它将莱维飞行产生的较大步长限定在解空间内，使莱维飞行机制既有效又不至于直接越界；X为在迭代范围[1，maxiter]内单调递减的凸函数，由当前迭代次数iter和最大迭代次数maxiter共同确定；C=4.5，为固定的常数，经过试错法重复实验得到，设计目的是在算法迭代后期削弱莱维飞行的能力，使算法趋向于局部收敛的过程；w是由问题的上下界、当前迭代次数和最大迭代次数、服从莱维分布的步长共同确定的自适应惯性权重，自适应权重对个体进行控制，以平衡算法的全局探索和局部开发能力。

为了保证算法具有足够的跳跃性，增加了一个提升算法跳跃能力的式（13），此公式产生的步长将有一定的概率替代经权重控制后产生的步长，本文将此概率设置为0.3。

2.3 变异算子池

在进化类算法中，通过变异可以丰富种群多样性，提高算法的全局搜索能力，避免算法陷入局部最优。为此，本文在TLBO 算法中设计了变异池策略（图1），在变异池中融入了两类变异操作，即基于差分进化（Differential Evolution，DE）算法的变异操作和基于遗传算法（Genetic Algorithm，GA）的变异操作。首先，差分操作是通过对不同个体间进行差分扰动操作产生更多潜在的解。差分进化算法的变异策略有多种，其中一类变异算子在单峰问题上表现突出，另一类变异算子在多峰问题上表现突出［33］。基于此，本文将差分进化算法的两类变异算子融合，以提升算法的全局探测和局部开发能力。其次经典遗传算法的变异操作则是针对个体进行的变异，遗传算法的变异算子也可以提升种群多样性，但由于涉及个体的重启操作，种群多样性会更高。遗传算法的变异算子分为均匀变异算子和非均匀变异算子：均匀变异算子产生的数值可均匀地分布到整个搜索空间，所以会提高算法全局探索能力；非均匀分布的变异算子则是对个体某些维度进行小范围随机扰动，提升算法收敛精度。综上所述，本文在变异算子池中融合了上述变异算子，在算法迭代进化过程中，针对某一个学习者个体，随机选择上述一种变异算子进行变异操作。变异算子池的引入平衡了算法的全局探索与局部勘探能力，在丰富算法种群多样性的同时也能够提升算法局部搜索的能力。

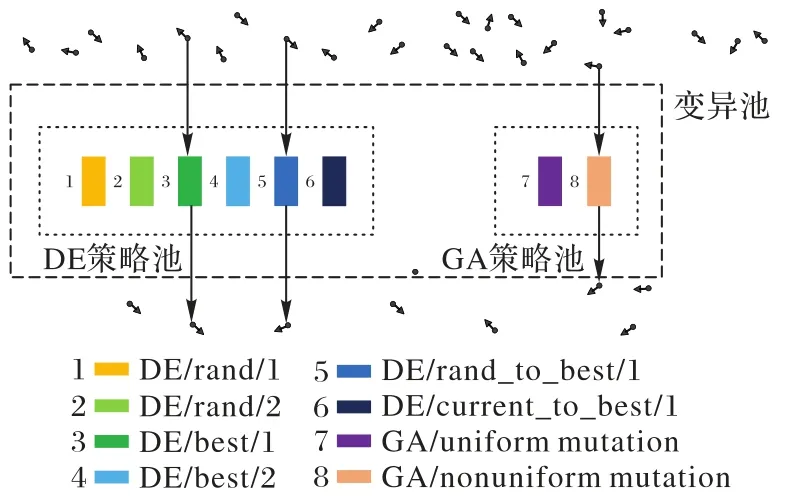
图1 变异算子池Fig.1 Mutation operator pool

3 实验与结果分析

3.1 测试函数

对ELMTLBO 算法在15 个国际测试函数上进行了多方面的评估。这15 个测试函数都是最小化问题，大小和复杂性各不相同，详情如表1 所示。需要注意的是，单峰函数只有一个最优解，而多峰函数有多个最优解；单峰函数用于评价优化算法的开发能力，而多峰函数则用于评价优化算法的探索能力。

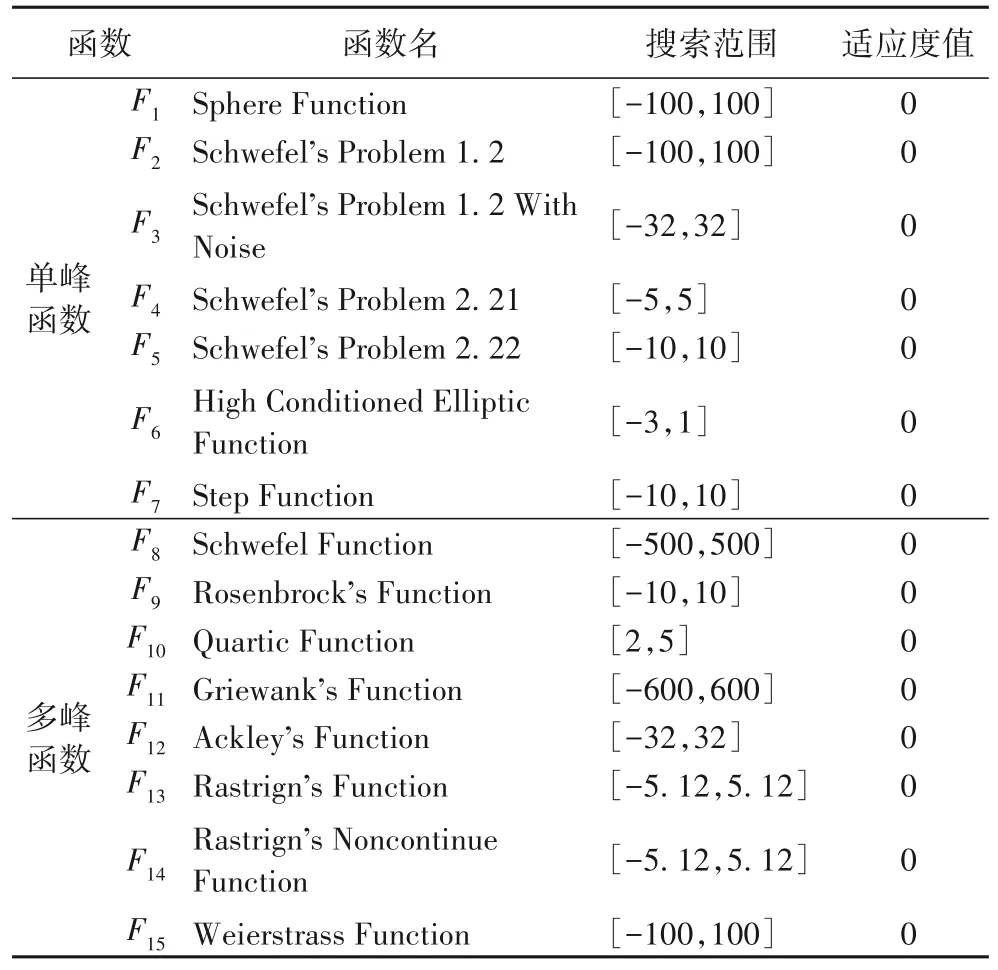
表1 测试函数Tab.1 Test functions

3.2 实验环境设置及评价标准

对比算法选择了几种先进的智能优化算法，包括：侏儒猫鼬优 化算法（Dwarf Mongoose Optimization Algorithm，DMOA）［34］、白鲨优化器（White Shark Optimizer，WSO）［35］、向量的加权平均数（weIghted meaN oF vectOrs，INFO）［36］、冠状病毒群体免疫优化器（Coronavirus Herd Immunity Optimizer，CHIO）［37］、平衡优化器（Equilibrium Optimizer，EO）［27］、樽海鞘算法（Salp Swarm Algorithm，SSA）［38］和Jaya 算法［39］；以及TLBO 和它的一些改进算法，包括：BTLBO、CTLBO、ETLBO、FETLBO、TLBOCIW 和OTLBO。

由于算法的不稳定性，为了使实验真实、公平，每组实验独立运行20 次，结果取平均值。在与先进的智能优化算法进行对比实验时，每个算法的最大评价次数（MaxFEs）为5×105，种群规模设置为40，决策变量维度设置为50；而在进行同类型TLBO 改进算法对比实验时，每个算法的最大评价次数为10×105，种群规模设置为40，决策变量维度设置为100。在以上实验中，所有结果统计表中均加粗标注表现最佳算法的平均值（Mean）和标准差（Std）。

各算法在15 个函数上均进行了测试，但为方便展示，仅列出有代表性的4 个测试函数的收敛曲线及箱图，其中：F4代表单峰函数，F8和F9代表复杂多峰函数，F14代表简单多峰函数。

3.3 不同类型算法的50维性能测试

与先进智能优化算法的对比结果如表2，图2 为部分函数的收敛曲线图。

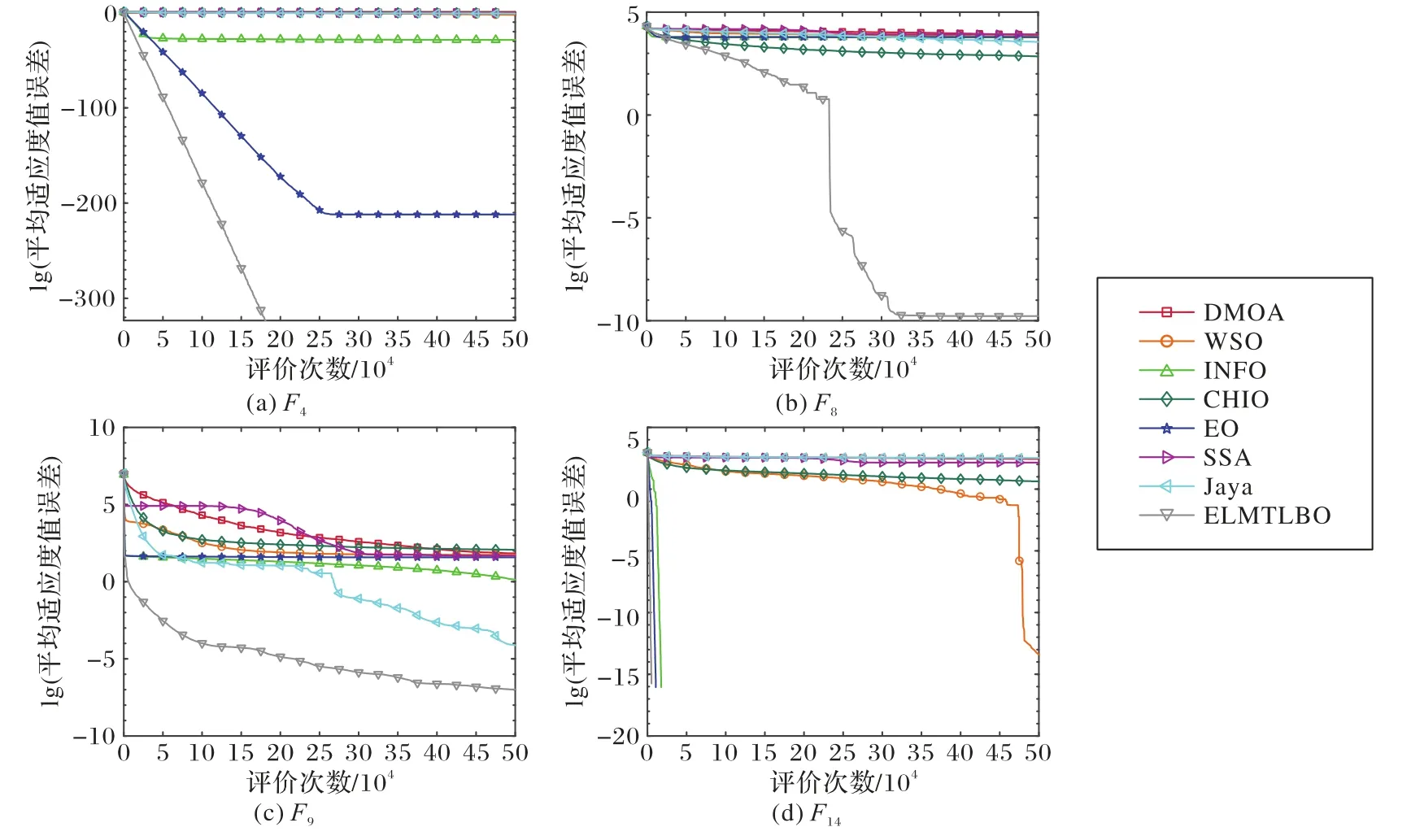
图2 不同类型算法针对50维问题在基准函数上的平均适应度值误差收敛曲线比较Fig.2 Comparison of fitness convergence curves of different types of algorithms on benchmark functions for 50-dimensional problems

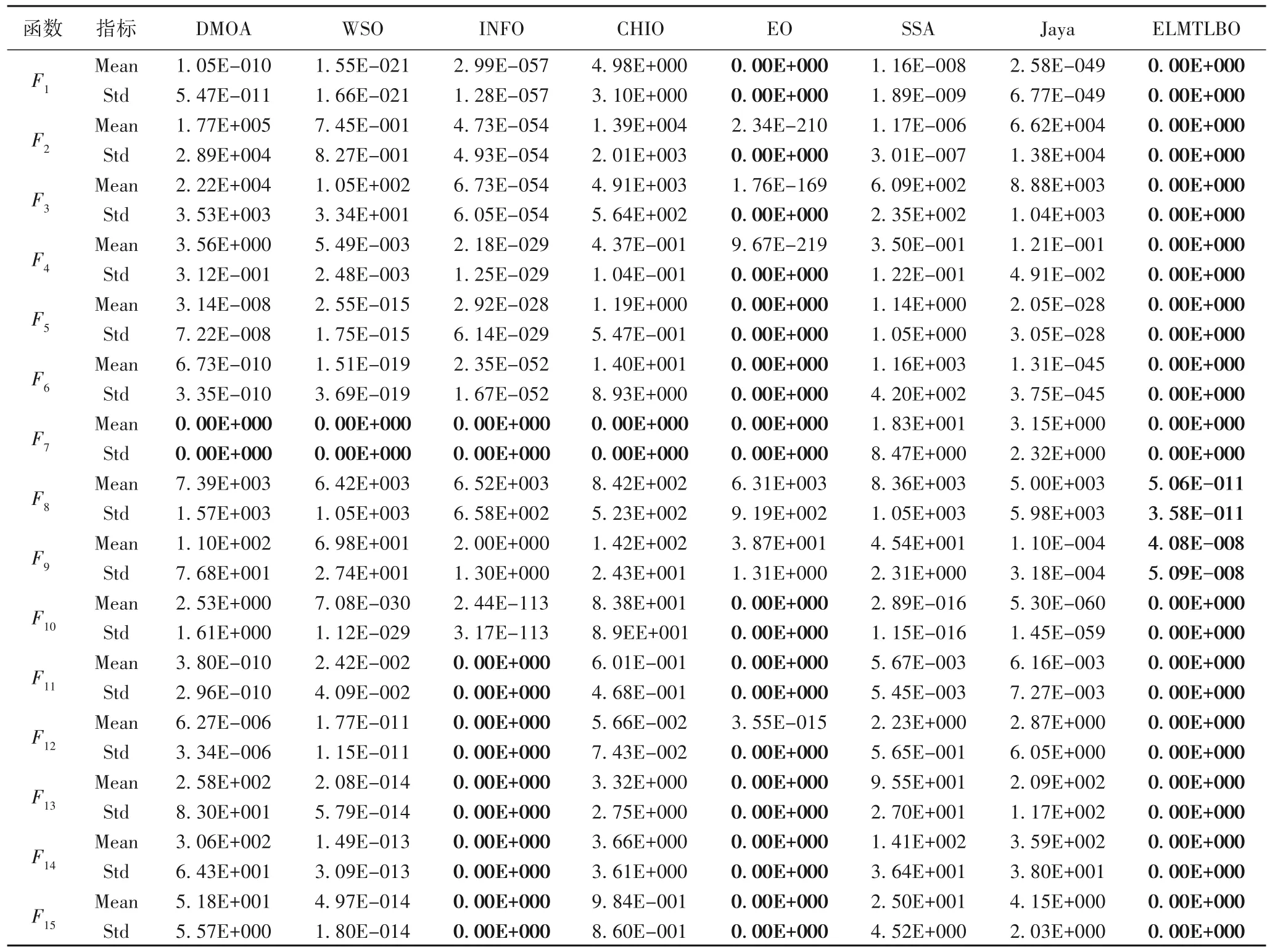
表2 ELMTLBO与不同类型算法针对50维问题在基准函数上的性能比较Tab.2 Performance comparison of ELMTLBO and different types of algorithms on benchmark functions for 50-dimensional problems

从表2 可以明显看到，ELMTLBO 在15 个测试函数上表现优秀，在其中13 个测试函数上均找到了全局最优解，而且在F8和F9上的性能最突出。在对比算法中，EO 表现较为优秀，它在9 个测试函数上找到了全局最优解，但是在F8和F9函数上表现不及ELMTLBO；表现最差的SSA 和Jaya 在任何测试函数上均表现不佳。结果表明，ELMTLBO 能够平衡算法的搜索能力，提高算法的综合求解性能。

从图2 可以明显看到，ELMTLBO 算法在F4函数上比EO等算法具有更高的收敛速度，且收敛精度也得到提升，基于莱维飞行产生的自适应权重可以使算法在前期快速收敛。在F14、F8、F9函数上，EO 算法在搜索后期陷入了局部最优，局部搜索能力弱，而ELMTLBO 借助莱维飞行机制以及变异算子池使算法能够在高速收敛的同时保证算法具有的逃逸能力。在F8函数上，ELMTLBO 依靠莱维飞行机制跳出了局部最优，从而使得收敛曲线突降；而在F9函数上，ELMTLBO算法的收敛曲线稳定下降，避开了其他算法易陷入的停滞点，验证了ELMTLBO 较其他算法更具有全局探索能力，依靠均衡引导及变异算子池增强的种群多样性，能避免算法陷入局部最优；同时在ELMTLBO 陷入局部最优且算法搜索停滞后，依靠莱维飞行使算法跳出了局部最优，从而使得收敛曲线急速下降。以上分析表明，ELMTLBO 与几种先进的智能优化算法相比，综合求解性能突出，能够高效求解各种问题。

3.4 同类型算法的100维性能测试

ELMTLBO 与TLBO 及它的一些改进算法的收敛精度如表3 所示，部分函数的收敛曲线图如图3 所示，比对箱图如图4 所示。

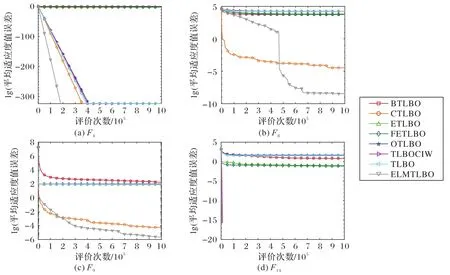
图3 ELMTLBO与TLBO算法变体针对100维问题在基准函数上的平均适应度值误差收敛曲线比较Fig.3 Comparison of fitness error convergence curves of ELMTLBO and TLBO algorithm variants on benchmark functions for 100-dimensional problems

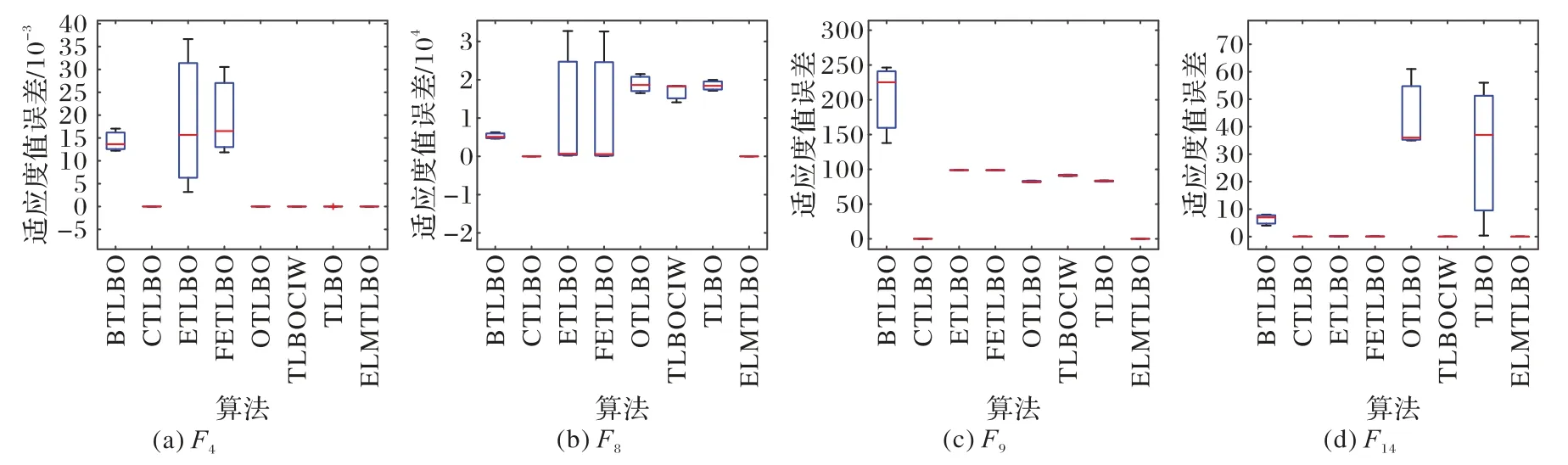
图4 ELMTLBO与经典TLBO改进算法针对100维问题在基准函数上的箱图比较Fig.4 Comparison of box plots of ELMTLBO and classic improved algorithms of TLBO on benchmark functions for 100-dimensional problems

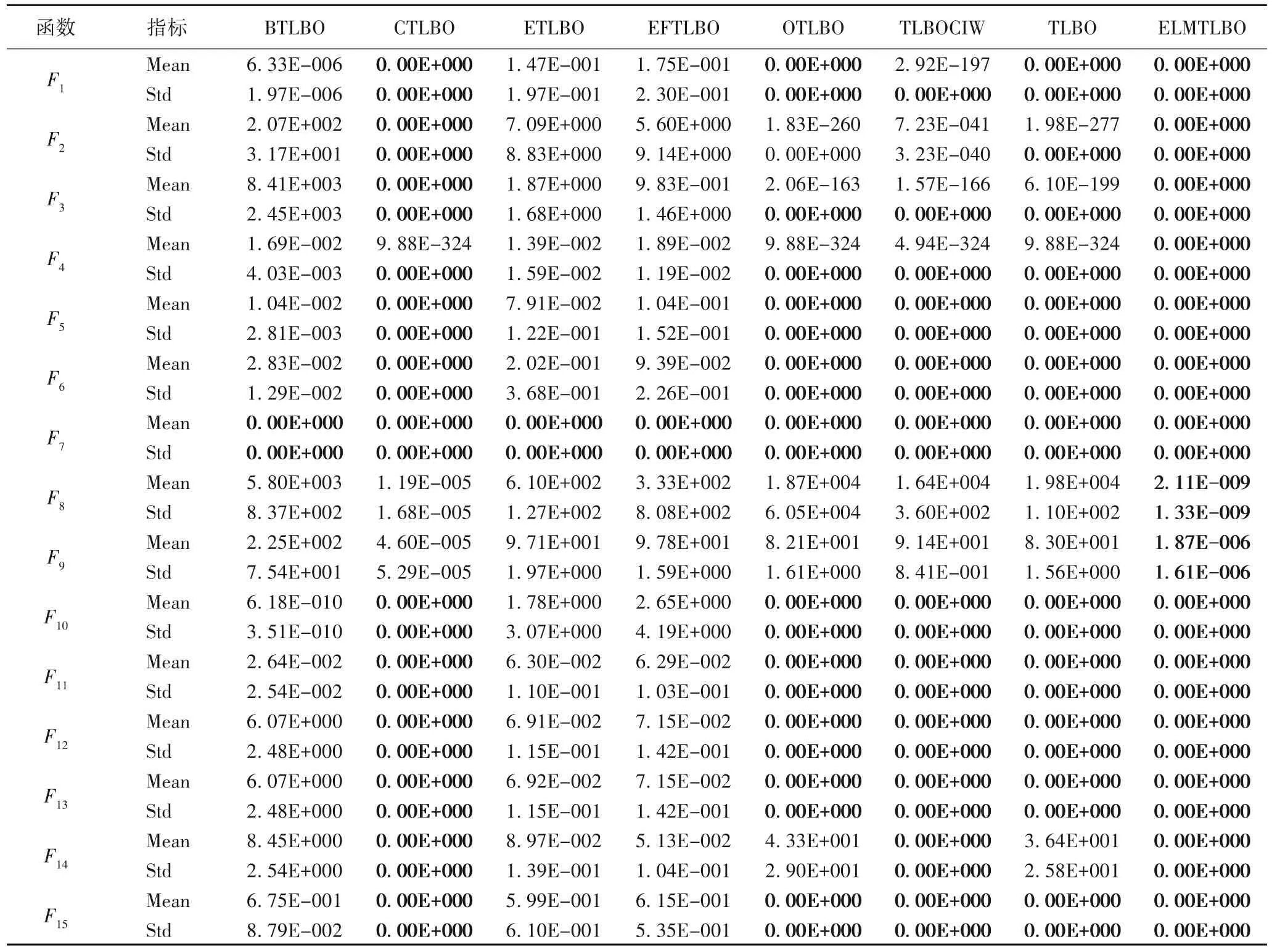
表3 ELMTLBO与同类型改进算法针对100维问题在基准函数上的性能比较Tab.3 Performance comparison of ELMTLBO and improved algorithms of the same type on benchmark functions for 100-dimensional problems

从表3 可以明显看到，大多数算法都可以在某些函数上找到全局最优，其中表现较为优秀的CTLBO 在12 个函数上收敛到全局最优，但在多峰函数F8、F9上性能却不及ELMTLBO；而ELMTLBO 在13 个函数上均收敛到全局最优，求解能力较强。除此之外，ELMTLBO 在F8和F9函数上的性能明显优于其他优化算法，这意味着ELMTLBO 在多峰函数上具有比其他改进算法更强的寻优能力，表明算法能很好地平衡全局探索与局部勘探能力。

从收敛精度图（图3）可以看出，TLBO 在F1函数上收敛较快，而在迭代后期陷入局部最优；TLBO、BTLBO 等算法在F8、F9和F14函数上出现早熟现象，并一直持续到迭代终止。面对解空间较大的多峰函数F8，依靠莱维飞行机制，在算法搜索中期收敛曲线出现了明显的跳跃，并在均衡引导和协同变异策略的引导下，算法继续精细化搜索。而在多峰函数F9上，表现相对较好的CTLBO 在迭代后期陷入了局部最优，而ELMTLBO 依靠均衡引导策略、莱维飞行和自适应权重策略、变异算子池策略的相互协作，仍可以使算法逐步向最优解逼近而不会陷入搜索停滞。

从图4 可知，ETLBO、FETLBO 算法结果数据较离散，显示出算法极大的不稳定性，这一特点在F4和F8上较为明显。CTLBO 和ELMTLBO 算法在所有测试函数的数据结果分布均较为集中，且结果的精度较高，验证了CTLBO 和ELMTLBO 算法具有稳定性及高效性。

整体来看ELMTLBO 算法在单峰问题和多峰问题上均表现出了卓越的性能，这说明本文对TLBO 的改进是有效的；而相较于其他经典的TLBO 改进算法，本文对TLBO 的改进效果更加显著。总的来说，ELMTLBO 具有可以应对复杂多样问题的综合能力。

3.5 完整性消融实验

为体现本文各策略的有效性，对ELMTLBO 算法中的三个策略进行完整性消融实验，在原始TLBO 算法中分别融入均衡引导策略（TLBOE）、基于莱维飞行的自适应权重策略（TLBOL）以及变异算子池策略（TLBOM），并与标准TLBO 和ELMTLBO 算法一起进行函数测试。参与测试的所有算法，均循环10 次，测试维度为30，最大评价次数为3×105，并对最佳适应度值取平均值。这些测试是基于CEC2005 和CEC2017 测试集中的部分测试函数进行的。表4 展示了不同改进策略的收敛精度情况。从表4 可以看到，带有均衡引导策略的TLBOE在F1、F5上优于TLBO 算法；带有自适应权重的TLBOL在F1、F5、F10、F13上优于TLBO 算法；带有变异算子池策略的TLBOM在F1、F5、F11、F13、F15上优于TLBO 算法。所有的改进策略都在不同测试函数上优于TLBO 算法，这说明每个策略在TLBO 算法上是有效的。而对于三个策略融合的ELMTLBO 算法，其收敛精度高于参与测试的任何算法，这表明所有改进策略都是相辅相成且稳定有效的，它们能够提升ELMTLBO 算法的综合求解能力。

表4 不同改进策略的结果对比Tab.4 Comparison of results of different improvement strategies

4 基于隐马尔可夫模型的多序列比对

多序列比对（Multiple Sequence Alignment，MSA）是为了揭示整个基因家族的特征，找出DNA 或RNA 序列的相似性或不相似性，可以判断同源基因间亲缘关系的远近，为预测或治疗疾病提供帮助，是一个NP 完全组合优化问题（Nondeterministic Polynomial Complete，NP-C）。MSA 目前缺乏快速有效的算法来解决比对问题，而使用隐马尔可夫模型（Hidden Markov Model，HMM）来解决多序列比对问题是一个热点方向。于是，本文使用ELMTLBO 算法优化HMM，并以此来求解多序比对问题。最终获得的基因序列可以用于基因溯源，可以收集、整理、检索和分析序列中表征蛋白质结构与功能的信息，并在相关病毒的疫苗或特效药研究等领域拥有较为突出的优势［40］。

4.1 MSA及HMM的相关概念

马尔可夫模型（Markov Model，MM）是数学中具有马尔可夫性质的离散时间随机过程，是用于描述随机过程统计特征的概率模型，其状态序列等于观测序列。而HMM 是一种特殊的离散时间有限状态链，与MM 最大的区别是：隐藏状态与观测状态分离。通常来说，HMM 可简化为一个三元组：

其中：π为初始概率向量；A为N阶转移概率矩阵；B为N×M阶生成概率矩阵。

HMM 是一个输出符号序列的统计模型，具有q个状态S1，S2，…，Sq，它们被分为三组：匹配（M）、插入（I）和删除（D）。此外，还有两种特殊状态：开始状态和结束状态。状态通过转移概率aij相互连接，它按一定的周期从一个状态转移到另一个状态，每次转移都会产生访问状态的路径和由路径上发射的可观察状态组成的序列。转移到哪一个状态，转移时输出什么符号，分别由转移概率和转移时的输出概率来决定。

当HMM 应用于MSA 时，观察序列以未对齐的序列形式给出，在序列对齐过程中通过对HMM 中参数的不断调整，最终找到产生最佳对齐的路径。这一过程可以使用前向算法和Viterbi 算法来确定HMM 生成给定序列o的概率，并得出产生o的最大概率的路径。最近研究表明，HMM 是解决MSA 问题的强大工具，针对MSA 的数学模型被描述如下：

1）为序列比对符号集合，Σ中包含基本字符集，若解决DNA 序列问题则包含A、C、G、T 四种碱基；若解决蛋白质问题，则包含20 种字符；“*”表示序列中的空缺。

2）S是待比对序列，具体表示为：

序列集合S包含q条序列，对于每一条序列Si，它由长度为Li的字符组成，序列中的sij代表一个符号。

3）扩展矩阵A为序列集S进行多序列比对后的结果矩阵：

其中：aij为Si序列的第j个字符的比对结果，该结果可能为“*”；M大于S集合中最长序列的长度。

4）F为矩阵A的度量函数，用来度量S中的各序列的相似程度。

以上就是MSA 数学模型的描述，多序列比对问题通过在序列集合S中进行适当的空位“*”插入，构建一个比对结果的矩阵A，使得打分函数F(A)达到最大。

4.2 基于ELMTLBO的多序列比对

更好的HMM 训练结果有助于得到更高质量的对齐序列，在使用ELMTLBO 算法训练HMM 时，训练过程中要保持HMM 的长度不变，只对HMM 的参数进行优化。HMM 的参数表示为粒子的位置，所有粒子均需要进行归一化处理以满足HMM 的约束条件。基于ELMTLBO 算法求解MSA 问题的求解步骤如下：

第一步 初始化HMM 模型，读取需要比对的基因序列文件，计算出基因所包含的序列条数lengthdata，确定最长的序列长度Lmax，以及比对后的序列长度L：

在确定比对后的序列长度后，计算出HMM 模型所需的参数个数，由此确定HMM 模型的基本结构，具体公式如下：

第二步 将待比对的序列和ELMTLBO 优化后的每个学习者的数据代入HMM 模型中，这里的学习者就是HMM 中的待优化参数。根据HMM 中数据的组成，将学习者中的Dim个数据分为HMM 模型基本要素对应的条件：初始概率向量(π)、转移概率矩阵(A)和释放概率矩阵(B)。

第三步 运用HMM 的计算原理调用Viterbi 算法求出每个学习者在该HMM 模型条件下的Viterbi 序列。

第四步 从Viterbi 算法计算得到Viterbi 序列后，相当于得到了一系列插入、删除、匹配状态的隐状态序列，根据序列匹配标准，将隐状态序列按照插入、删除和匹配三个状态分别对齐，得到的是比对后的数字序列。

第五步 使用配对分数和函数（Sum of Pairs Score，SPS）计算序列比对结果的得分情况，这里的SPS 函数就是多序列比对问题的适应度函数。SPS 公式如下：

其中：li是比对过的序列，lj是待比对的序列，Dis是两个序列间的距离矩阵。

第六步 当迭代完成后，将最优数据代入HMM 模型中，通过Viterbi 算法回溯得到得分最高的比对后的基因序列。

4.3 序列比对测试

选取的实验对象分别为国际基准序列比对数据库BALiBASE 基因序列数据库中的“451c_ref1”基因序列（图5（a））、“1ad2_ref1”基因序列（图5（b））、截断“kinase_ref1”基因序列（图5（c））及“kinase_ref1”基因序列（图5（d）），同时为了验证ELMTLBO 算法的比对精确度，选取wPSO（weighted PSO）算法、GA、EO算法、TLBO算法作为实验的对照算法。

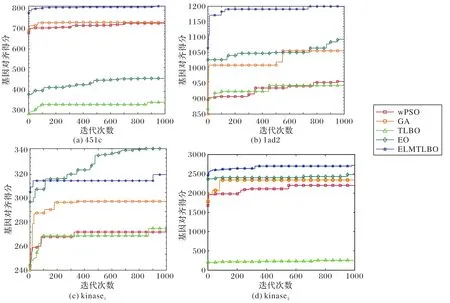
图5 各算法在各基因序列上的得分情况Fig.5 Score of each algorithm on each gene sequence

实验参数设置如下：每个算法独立运行10 次，每次迭代1 000 次。算法初始搜索范围为［0.2，0.8］，由于MSA 问题解空间上下界范围不明确，故取消各算法越界限制条件。算法参数设置如表5。

表5 算法参数设置Tab.5 Algorithm parameter setting

表6 为不同算法在各基因序列上的比对结果及相关序列信息，其中：Name 表示对比序列样本名称，并在名称后附打分结果图标号；lengthdata为样本序列组中序列数目；LSEQ(m，n)表示样本集中序列的长度范围，其中m为最小长度，n为最大长度；Dim表示HMM 中需要优化的参数个数，即优化算法搜索空间的维度；Score为算法最优得分。在实验过程中，计算SPS 得分项来生成算法的多序列比对结果打分图（如图5 所示），T为算法独立运行一次，即算法迭代1 000次的平均消耗时间（单位：s），加粗标记比对精度结果。

表6 不同算法的多序列比对结果Tab.6 Results of multiple sequence alignment of different algorithms

从表6 和图5 可以看出，ELMTLBO 在lad2、451c 及kinase序列上表现不俗，虽然面对维数在上千到上万的高维问题，算法寻优速度仍然较快，显示出了卓越的问题求解能力，同时算法在迭代后期也有继续收敛的潜力。这一点也同样在EO 算法上体现。与TLBO 算法相比，ELMTLBO 算法的Score得分值高，求解精度较高，说明对算法的改进是有效的。

图6 和图7 分别为截取的kinase 基因进行序列比对前后的结果，其中①～⑤分别表示kcc2_yeast、dmk_human、kpro_maize、lcsn 和daf1_caeel，是kinase 基因中的序列段。从图7 可以看到，EMTLBO 算法优化后的HMM 可以精确对齐kinase 序列段。与其他优化算法相比，ELMTLBO 算法能够提升多序列比对精度，从而获得较精确的基因序列比对结果，同时也验证了ELMTLBO 算法具有解决现实世界问题的能力。

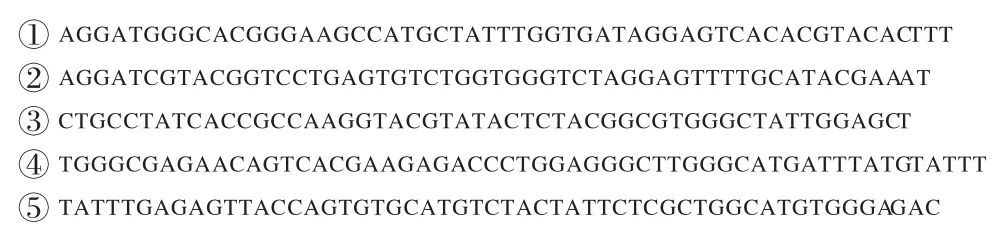
图6 kinase的部分基因序列Fig.6 Partial gene sequences of kinase

图7 比对后的kinase部分基因序列Fig.7 Partial gene sequences of kinase after alignment

5 结语

为解决标准TLBO 算法易陷入局部最优、算法早熟、收敛精度不高等问题，本文提出了一种改进的基于教与学的优化算法ELMTLBO。该算法将莱维飞行与自适应权重融合，自适应更新个体水平，偶尔产生较大的权重使算法具有跳出局部最优的能力；融合DE 算法变异算子和GA 算法变异算子，设计了一种变异算子池，在提升种群多样性的同时，也能够提升算法的收敛精度。仿真结果表明，ELMTLBO 算法比其他参与测试的算法具有更强的寻优能力，在实验提供的大部分测试函数上均能够找到理论最优解。最后将ELMTLBO算法应用于多序列比对问题中，优化HMM 模型中存在的参数。实验结果表明，ELMTLBO 算法能够有效地平衡搜索能力，即使面对高维且复杂得多序列比对问题，仍能够快速且精确地获得基因序列比对结果。由于ELMTLBO 是一种多策略算法，如何合理使每种策略发挥最大效能是一个需继续深入探究的问题，未来EMLTLBO 应引入更多的自适应机制，在算法不同的搜索阶段使用不同的策略进行更高效的搜索，并将其继续应用于更多的实际问题，如图像分割、PID 控制器优化、路径规划等。