基于自抗扰控制的轮毂电机驱动电动汽车耦合振动抑制*

张海军 万少华 张明杰

（湖北文理学院，纯电动汽车动力系统设计与测试湖北省重点实验室，襄阳 441053）

主题词：轮毂电机 随机激励 耦合振动 自抗扰控制

1 前言

轮毂电机驱动电动汽车动力传输效率高、污染小、控制灵活，尤其可以实现对单个车轮的独立控制，因此具有明显的驱动控制优势[1]。然而，相对传统的动力中置电动汽车而言，轮毂电机省去了机械传动系统，电机更加靠近振动源，使其运行条件更加恶劣，同时电机在运行过程中还存在各类不确定性扰动，如路面的随机扰动和自身电磁激励[2]。工程上采用传统比例积分微分控制方法抑制不确定性扰动，虽然实现简单，但始终存在转速超调与快速跟踪之间的矛盾，在复杂扰动条件下跟踪精度不高，制约了车辆动力性能的提升[3]。自抗扰控制（Active Disturbance Rejection Control，ADRC）在“基于误差来消除误差”并吸取现代控制理论方法的基础上具备扰动估计和补偿能力，控制效果好且计算量不大，可极大改善电机控制性能[4-6]。

很多学者针对自抗扰控制在电机上的应用开展了研究。文献[7]针对永磁同步电机，基于自抗扰控制设计进行了综述，并给出了未来研究方向；文献[8]提出了基于比例谐振自抗扰控制的永磁同步电机电流解耦及谐波振动抑制方法；文献[9]分析了自抗扰控制下飞机牵引车的变速动态特性及振动控制；文献[10]分析了基于自抗扰控制的轮毂电机在负载转矩扰动和模型失配扰动条件下的响应情况；文献[11]和文献[12]分别研究了基于自抗扰控制的车辆制动性能和电动汽车定速巡航控制策略。目前，自抗扰控制的相关研究大多集中于传统电机，很少涉及轮毂电机的使用场景。轮毂电机省去了机械传动系统，更加靠近激励源，使其受到更严重的路面激励和不平衡电磁激励双重作用。

本文针对路面不平度和偏心电磁力引起的电磁耦合激励对车辆振动特性及平顺性的影响进行分析，建立车辆1∕4振动系统模型，提出一种基于自抗扰的振动抑制方法，并建立轮毂电机驱动电动汽车振动控制模型，将路面随机激励和轮毂电机自身产生的电磁激励视为总扰动进行统一观测补偿，最后通过MATLAB∕Simulink仿真软件对所提出的控制策略进行仿真验证。

2 轮毂电机驱动电动汽车振动分析

2.1 1/4车辆振动模型

轮毂电机驱动电动汽车振动系统主要由2 个子系统组成，即汽车悬架系统和轮毂电机系统。为了简化分析，本文建立1∕4车辆振动模型，如图1所示。

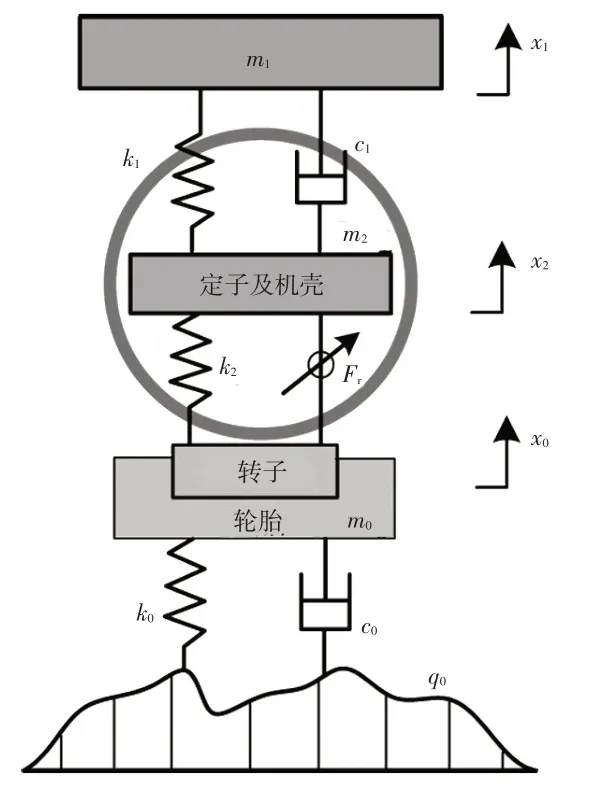
图1 车辆1∕4振动模型

根据牛顿第二定律，车辆振动系统的振动方程为：

式中，m1、m2、m0分别为车辆簧载质量、电机定子质量、电机转子及轮胎轮毂质量；x1、x2、x0分别为簧载质量位移、电机定子位移、轮胎轮毂位移；q0为随机路面激励位移；k0、k1、k2分别为轮胎刚度、悬架刚度和电机轴承刚度；c0、c1分别为轮胎阻尼和悬架阻尼；Fr为电机内部不平衡电磁力。

2.2 轮毂电机数学模型

本文以表贴式外转子永磁同步电动机为例，忽略电机铁芯饱和及涡流磁滞损耗，则电机在转子坐标系中状态方程为：

式中，Ud、Uq分别为定子d、q轴电压；id、iq分别为定子d、q轴电流；Rs为定子相电阻；L为绕组自感；ψf为转子永磁体磁链；np为极对数；J为转动惯量；B为黏滞摩擦系数；ωe为电角速度；TL为负载转矩。

电机d、q轴磁链方程和电压方程为：

式中，φd、φq分别为d、q轴磁链；Ld、Lq分别为定子d、q轴轴电感。

表贴式永磁同步电机的定子电感满足Ld=Lq，由机电能量转换原理可知，电磁转矩Te为：

当电磁转矩Te和负载转矩TL不相等时，将导致电机转速的改变，同时产生角加速度ωr，由力学原理知，电机机械运动方程为：

2.3 随机路面激励输入分析

路面不平度是影响车辆振动输入的主要来源，且具有随机性，常用道路激励来表示：

式中，n为空间频率，为波长的倒数；n0=0.1 m-1为参考空间频率；Gq(n0)为参考空间频率下的路面功率谱值；ω为频率指数，一般取ω=2。

以时间频率表示的路面不平度功率谱密度在整个时间频率范围内为白噪声，用一定条件下的白噪声代替路面的随机激励，可表示为：

式中，v为车速；f0=0.01 Hz 为下限截止频率；q0(t)为随机路面不平度随时间变化的幅值；ω(t)为均值为0、强度为1的单位白噪声道路干扰。

仿真选用的系统相关参数如表1所示，设置车速为60 km∕h，粗糙度系数为64×10-6的B 级路面不平度位移输入如图2所示。

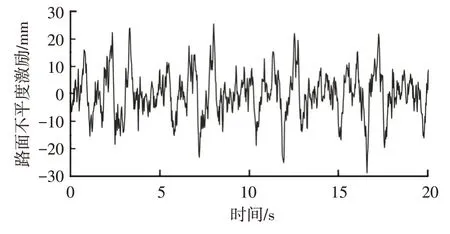
图2 B级路面不平度位移输入

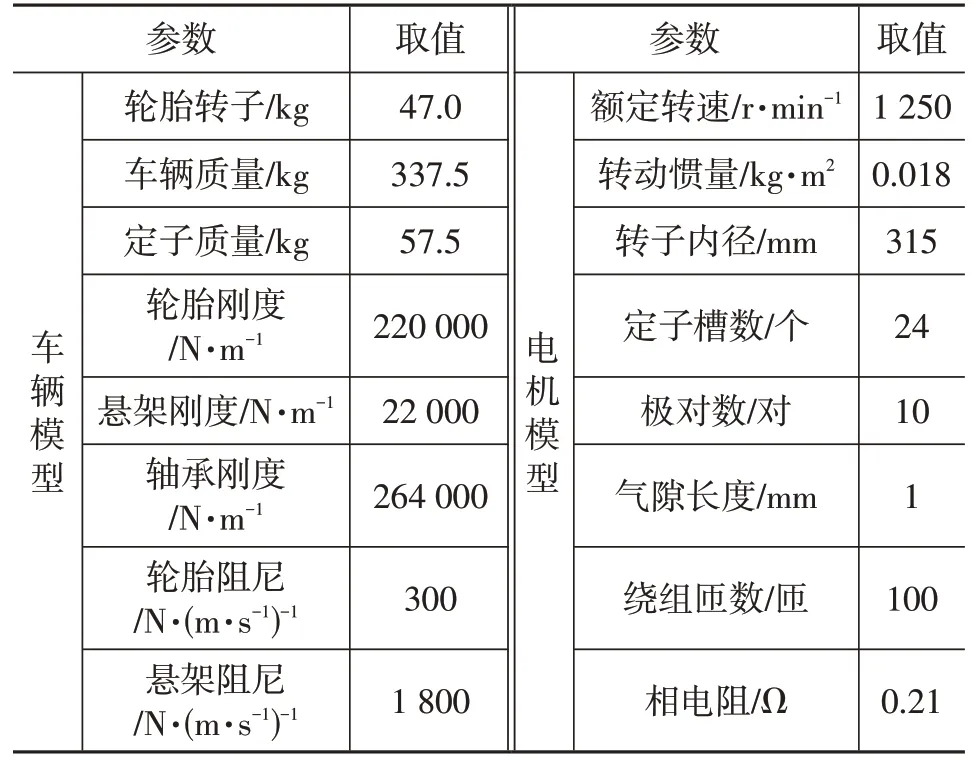
表1 模型主要参数

不考虑电磁激励时，以路面谱作为车辆振动系统输入的激励源，选取车身加速度、轮胎相对动载荷、车身位移和电机位移作为车辆平顺性指标，得到车辆系统响应如图3所示。

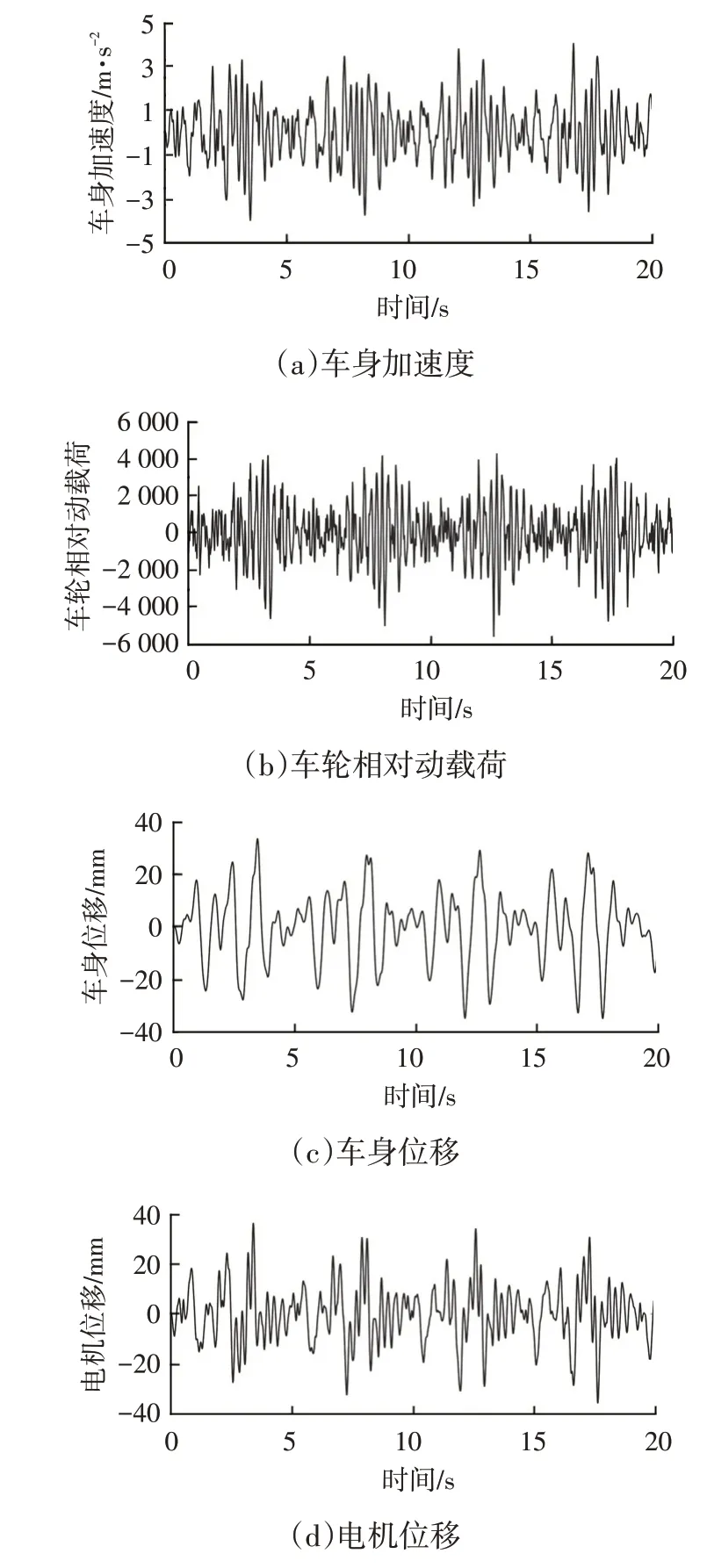
图3 单独路面激励时的系统响应

2.4 耦合振动输入分析

轮毂电机驱动电动汽车行驶过程中，在复杂路况等随机因素的影响下，定、转子极易出现旋转轴线不对称的现象，使得电机定、转子之间气隙分布不均匀，从而产生气隙偏心现象，加剧车辆及电机振动。以B级路面上车速60 km∕h为例，得到电机定、转子偏移量变化情况如图4所示。

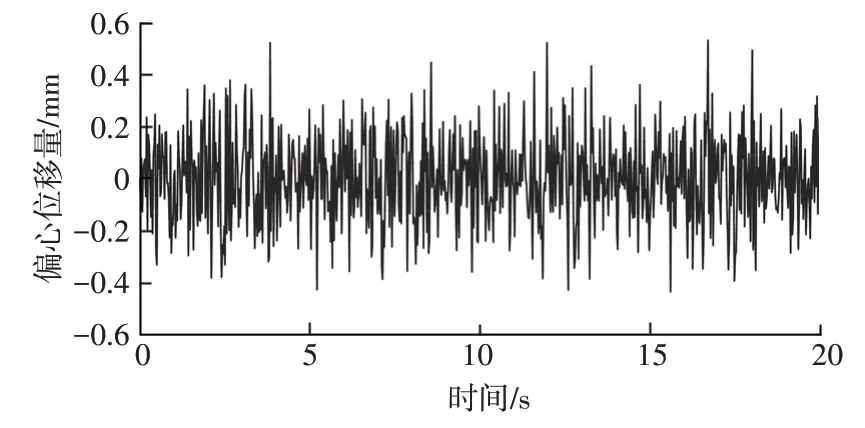
图4 轮毂电机定、转子偏移量

轮毂电机动态偏心时其气隙长度gp随时间变化：

式中，ge为定子周向气隙长度；hm为永磁体径向厚度；μr为相对磁导率；θ为机械角度；ep为偏心距。

电机气隙的偏心不会影响电机定子和转子磁动势，但是气隙偏心会导致气隙磁导发生变化，从而产生不平衡电磁力。本文的研究对象为表贴式永磁同步电机，为得到最优的转矩控制，可将全部相电流作用于交轴，且d轴电流为0，转子之间的气隙长度最小位置随转子的旋转发生周期性改变，气隙磁导λd及电感L可表示为：

式中，ε=ep∕(ge+hm∕μr)为有效气隙长度；μ0为磁导率；N为定子匝数。

路面不平度引起的轮毂电机气隙偏心会在一定程度上加剧电机和车辆的振动，因此有必要分析路面激励与电机电磁耦合作用对车辆平顺性的影响。同样设置仿真条件为B级路面，车速60 km∕h，得到系统响应如图5所示。

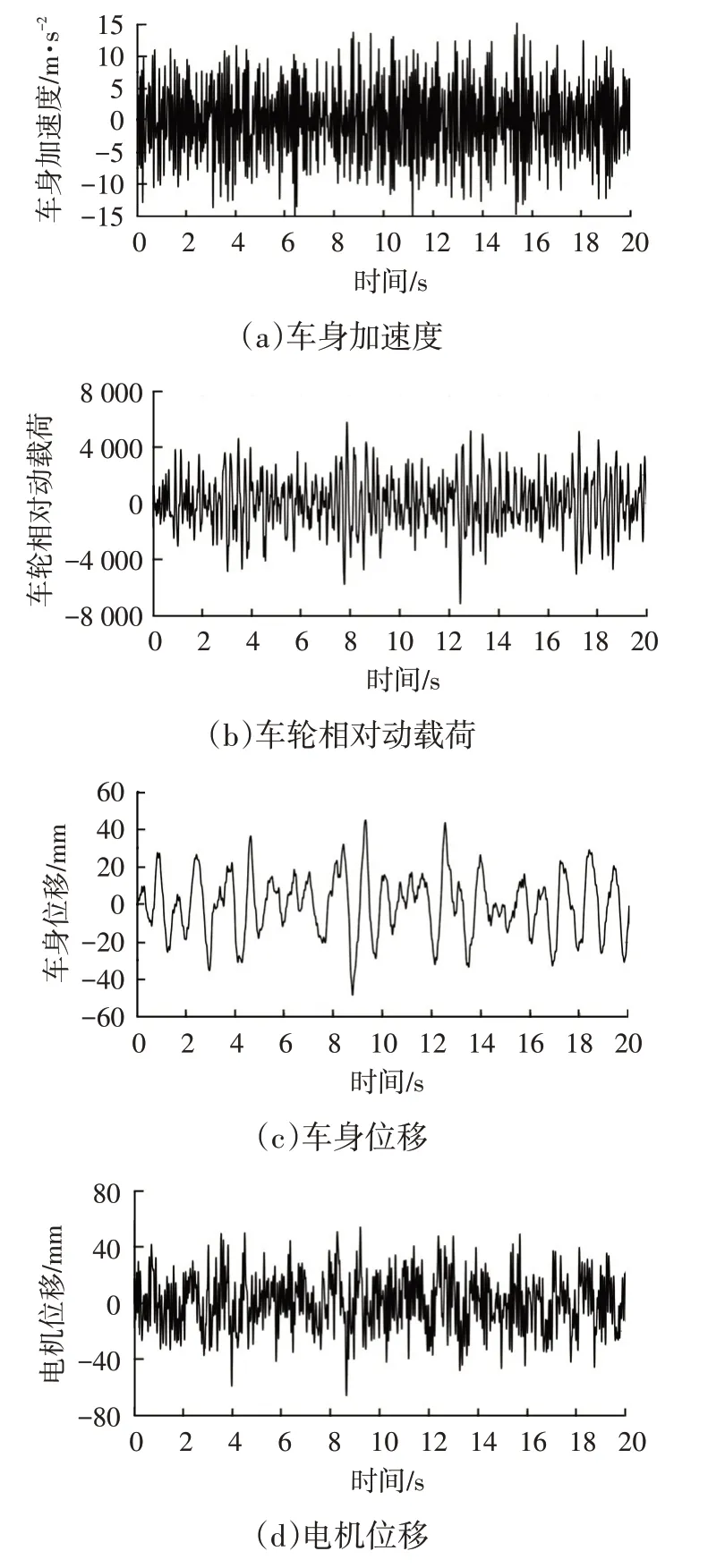
图5 耦合激励下系统响应

由图3a和图5a可知，在无偏心电磁力作用时，车身加速度为4.2 m∕s2，在路面激励和不平衡电磁力耦合作用下，车身加速度增大了58.8%。由图3b和图5b可知，相比路面激励单独作用时，电磁耦合激励使得车轮动载荷增加22.2%，同时，车身位移和电机位移分别由0.034 m和0.036 m增加到0.048 m和0.062 m，增加幅度为41.0%和72.0%。上述结果进一步验证了路面不平度会对轮毂电机气隙产生较大的影响，随着气隙偏心的增大，产生的不平衡电磁力加剧了车辆及电机系统的振动，同时，二者的耦合作用又将增大轮毂电机的气隙偏心，使车辆操纵稳定性和乘坐舒适性严重恶化。因此，对路面激励和轮毂电机产生的不平衡电磁力的耦合振动进行抑制非常必要。

3 轮毂电机自抗扰控制器设计

3.1 ADRC抗干扰机理

ADRC能够有效提高轮毂电机的抗干扰能力，主要原因在于其将被控对象的内扰和外扰视为综合扰动并对其进行统一观测补偿。扩张状态观测器是自抗扰控制器设计的核心部分，其通过观测状态变量并给出扩展状态变量从而得到系统的总和扰动。以系统的实际输出y和控制变量u来跟踪估计系统的状态变量和扰动量，可表示为：

式中，e为输出信号与跟踪信号的差值；h为采样时间；fal为包含线性区域的幂函数；δ为区间长度，可避免误差小时高增益引起抖振；z1、z2分别为观测值及微分信号；z3为总扰动估计量；β01、β02、β03为控制增益；fe、fe1分别为不同参数下fal的输出量；b0为综合扰动调整系数。

其中，幂函数fal可表示为：

式中，sgn为符号函数；α为观测变量阶数参数。

非线性状态误差反馈控制通过对误差及其微分信号进行非线性组合来得到更好的控制效果，同时通过扰动估计补偿进行校正。可以表示为：

式中，e1、e2分别为过渡过程量与输出观测量及输出观测微分的误差；u0为初始控制量；r1为误差反馈速度跟踪因子；v1、v2分别为安排过渡量及其微分信号。

3.2 控制器设计

在传统的控制方法中，位置或速度出现误差后系统才进行调节，将存在一定的控制迟滞。为更好地进行控制，需在扰动出现时迅速进行抑制，在确定研究对象和控制变量后，由轮毂电机数学模型得到变量关系为：

一阶自抗扰控制系统状态方程可表示为：

式中，w(t)为外部扰动；f(x,w(t),t)为综合扰动。

一阶自抗扰控制没有考虑跟踪微分器和扩张状态观测器中的微分作用，然而，在控制系统中微分量具有一定的预测功能，因此，考虑到轮毂电机运行时各项扰动因素，本文选用二阶控制器提高控制效果。选取机械角速度为状态变量x，交轴电流为控制变量u，y为输出变量的二阶系统为：

对比一阶控制器可知，本文综合扰动f(x)和综合扰动调整系数b0分别为：

自抗扰控制器虽由不同模块组合而成，但各模块间参数却没有明确的数学联系，基于自抗扰控制器的“分离性原理”，在确保各模块运行不受影响的条件下对各部分参数进行整定。自抗扰控制的采样时间h是提前设定的，因此，可将各部分参数以采样时间为纽带进行相关整定。

对于扩张状态观测器（Extened State Observer，ESO）而言，其系统动态特性主要由z3的控制增益决定，且取值与跟踪迟滞成反比，为了减小跟踪迟滞，可增大β03，但增益过大会造成对应的跟踪振荡，此时可通过调节z1和z2所对应的增益来减小振荡，从而得到较好的跟踪效果，同时可用采样时间来代替线性区间δ的取值。参数整定可表示为：

对于非线性状态误差反馈控制（Nonlinear State Error Feedback，NLSEF）而言，误差反馈速度跟踪因子的取值与系统的调节速度成正比，因此尽可能增大r1，从而提高系统的调节速度。由于扰动调整系数同时与控制量和ESO有关，当被控对象数学模型确定时可直接得到，若未知，可在真值30%附近选取，依然可以获得最优控制效果[13]。

4 仿真分析

为验证本文所提出的控制策略的有效性，基于MATLAB∕Simulink搭建轮毂电机模型，控制器参数如表2所示。

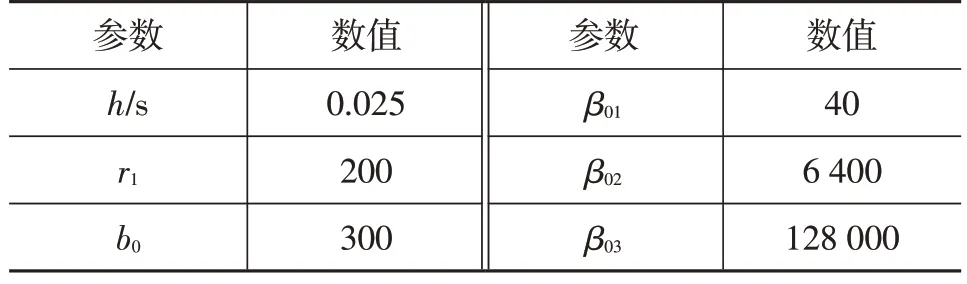
表2 控制器参数

设置仿真条件为B级路面，车速60 km∕h，耦合振动为正常激励，通过ADRC进行优化调节得到系统响应如图6所示。

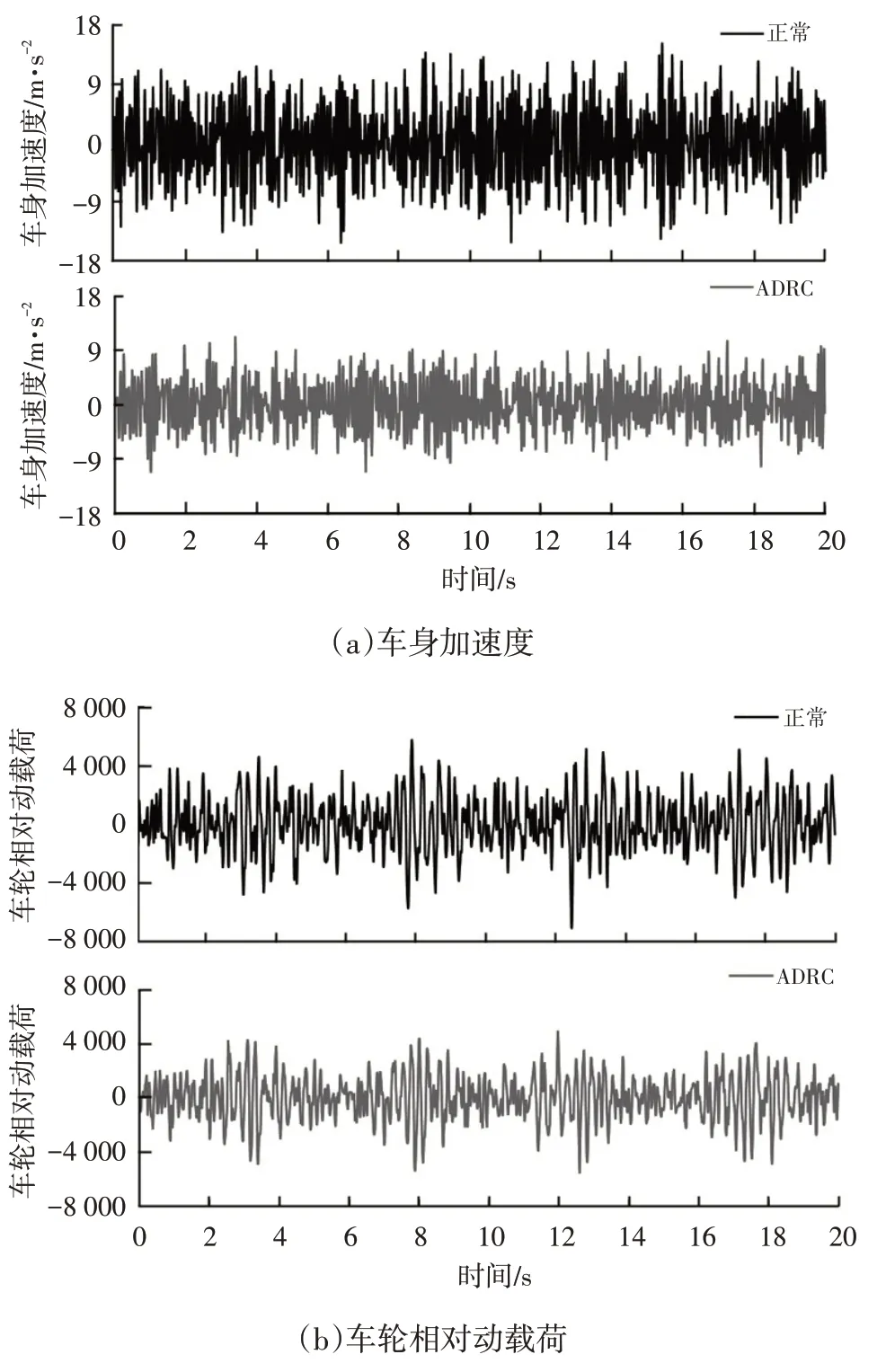
图6 ADRC调节下的系统响应

由图6a可知，在耦合激励下，车身加速度最大变化幅度为15.1 m∕s2，通过ADRC 进行优化后，加速度最大变化幅度为8.0 m∕s2，车身加速度振动幅度下降了47.0%；由图6b可知，在耦合激励作用下，车轮动载荷在第12.2 s时达到最大值7 200 N∕m，优化后的车轮动载荷最大值为5 100 N∕m，优化幅度为29.2%，相比路面单独激励作用时下降了9.8%；由图6c和图6d可知，在耦合激励作用下，车身位移和电机位移最大变化幅度分别为0.048 m 和0.062 m，由于轮毂电机更加靠近耦合激励源，电机位移变化是车身位移变化的1.29倍，进一步说明轮毂电机的运行条件更为恶劣，优化后车身和电机最大位移分别为0.036 m和0.035 m，相比耦合激励调整后的位移下降幅度分别为25.0%和43.5%，同时与路面单独激励相比较时，通过优化调整后的电机位移相比车身位移下降幅度更大。上述结果验证了自抗扰控制的扰动补偿能力对在复杂工况下运行时产生电磁耦合振动的轮毂电机来说更具优越性和兼容性。

5 结束语

本文通过分析路面随机激励和电磁耦合激励对轮毂电机驱动电动汽车的振动特性及车辆平顺性的影响，提出一种自抗扰控制策略，基于MATLAB∕Simulink进行仿真验证，得出以下结论：

a.相比单独的路面激励，气隙偏心引起的电磁耦合激励使得悬架系统及电机系统的振动幅值分别增加了41.0%和72.0%，说明电磁耦合振动对轮毂电机运行时的影响更加严重。

b.针对电磁耦合振动引起轮毂电机驱动电动汽车系统的动态响应，本文所提出的控制策略能够将悬架系统及电机系统的振动幅值分别降低25.0%和43.5%，表明自抗扰控制对电磁耦合振动具有很好的抑制效果。

c.相比车身的优化调整幅度，优化后电机的幅值比路面单独激励时动态幅值更低，表明自抗扰控制技术对电磁力引起电机振动的抑制效果更具优越性。