可调导叶对气悬浮离心压缩机及系统性能影响研究

宋君楠 巩捷明 刘义腾 刘广彬

（青岛科技大学机电工程学院 青岛 266061）

0 引言

离心压缩机作为冷水机组的核心设备，被广泛应用于大型制冷空调系统、工业制冷等领域。采用气悬浮轴承的离心制冷压缩机成为未来发展方向之一[1]，气悬浮离心制冷压缩机克服了传统齿轮增速高能耗的缺点[2]，同时具有成本低、不需要主动控制等优点[3]，已成为近年的研究热点。离心式压缩机常用的调节方法有进出口节流调节、可调进口导叶调节、可调叶片扩压器调节和变转速调节等，其中，可调进口导叶（variable inlet guide vanes，简称VIGV）调节是通过改变叶轮进口前导叶的角度，使气流产生预旋的调节方法[4-6]。可调进口导叶调节范围宽，可以在压缩机运行时进行实时调节，使其在许多工业生产领域有着广泛的应用[7]。

目前，已有不少学者对带可调导叶的离心压缩机性能进行了相关研究，但关于可调导叶对系统循环特性的影响的相关研究还比较少。如刘波等[8]模拟了不同进口导叶弯度时压气机内部流场，得到了相应的流场结构和性能参数，改善了压气机的性能。闫雪等[9]通过数值模拟研究了带级间冷却的双级离心压缩机变导叶联合调节性能，通过内部流动分析，得出了单级变导叶调节以及双级联调时压缩机的性能变化规律。Tian 等[10]对某用于大型空分装置的闭式离心压缩机进行了仿真模拟，通过与实验数据进行对比，分析了导叶开度对离心压缩机性能特性和进口流场的影响。田红艳等[11]针对进口端壁导叶对离心压气机的特性影响进行了仿真研究，发现导叶正预旋使压气机的阻塞流量和喘振流量向小流量方向偏移，导叶负预旋使压气机特性向大流量工况偏移。曲帅杰等[12]通过数值模拟的方式，对比了内部的流动状况，研究了不同开合角度的进口导叶对离心叶轮性能的影响。李帅等[13]数值研究了导叶正预旋对离心压缩机气动性能和内部流动的影响，研究发现导叶正预旋调节使得压缩机级的性能曲线向小流量方向移动，拓宽了压缩机级的小流量工况范围。Tan 等[14]数值研究了径向进气道对带可调导叶离心压缩机性能的影响，通过与轴向进气道模型进行比较，发现径向进气道模型整体级多变效率平均降低了4%，总压比平均降低了3.3%。Meng 等[15]搭建了压缩空气储能用高压离心式压缩机试验台，通过对比导叶开度在-20°～+50°时的实验数据与CFD 模拟结果，得到了不同导叶开度下压缩机的性能曲线。Romei 等[16]模拟研究了某带可调导叶的大型超临界二氧化碳离心压缩机，分析了不同导叶开度下压缩机内部流场情况，得到了不同预旋角下压缩机流量范围变化及性能规律。Li等[17]数值研究了小流量下正预旋对离心压气机的气动性能和内部流场的影响，认为可调导叶可以有效改善小流量下压气机的不稳定流动，喘振裕度相比无预旋情况提高了约9.95%。受到制冷剂物性、复杂运行工况等的限制，针对气悬浮离心式制冷压缩机的研究仍较少，其宽工况运行性能及调节特性尚不明确，研究导叶、转速等调节方式对其性能的影响与对压缩机级系统稳定、高效运行具有重要意义。

对于气悬浮冷水机组，要求压缩机具备较宽的流量调节范围，通过调节进口导叶开度拓宽压缩机工作裕度是重要手段。因此，本文采用CFD 方法模拟了带进口导叶的气悬浮双级离心压缩机内部流场及变工况运行特性，分析了导叶对系统循环特性的影响，为气悬浮离心式冷水机组宽工况运行提供了参考。

1 理论分析

本文所采用的气悬浮冷水机组原理是在基本的双级压缩制冷系统的基础上，增设了冷却电机回路与轴承供气系统，工作流程如图1 所示。来自蒸发器的制冷剂蒸气经低压级压缩机后压力提高至中间压力，随之同经济器出来的制冷剂蒸气混合，再进入高压级压缩机压缩，之后共同进入冷凝器。在进入冷凝器前，制冷剂蒸气需分出一小部分流量对轴承进行供气。冷凝后的高压液体分为三路：一路在节流阀节流后进入经济器蒸发后进入级间管道，一路用于电机冷却，而另一路则经经济器内过冷后通过电子膨胀阀节流后进入蒸发器，完成整个循环。

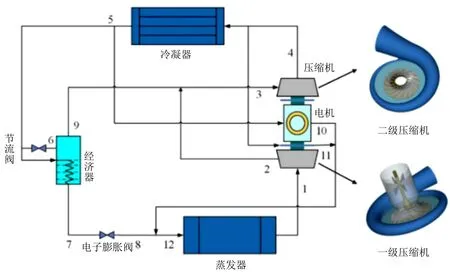
图1 气悬浮制冷循环流程图Fig.1 Flow chart of refrigeration cycle with gas bearings

为了拓宽冷水机组的工作裕度，在一级压缩机进口安装可调开度的导叶，以增加进气预旋，导叶、叶轮、扩压器和蜗壳的主要参数如表1 所示。

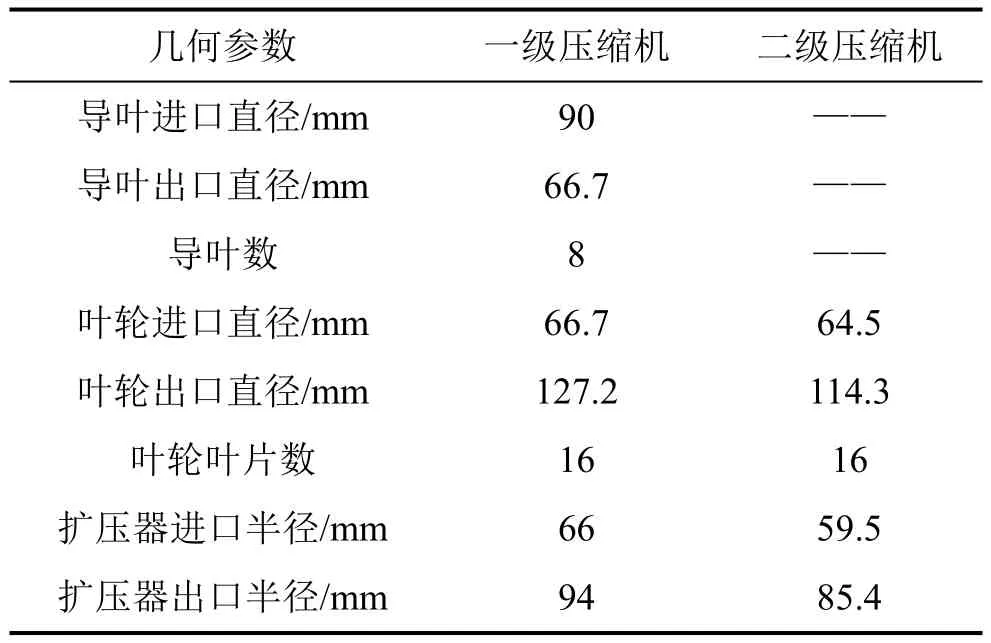
表1 双级离心压缩机主要几何参数Table 1 Main geometric parameters of two-stage centrifugal compressor

2 数学模型

本文采用CFD 的方法对离心压缩机的内部流动进行分析，针对其稳定运行工况，采用稳态流动模拟离心压缩机内部流场。压缩机内流体在流动过程中的基本控制方程主要包括质量守恒方程、动量守恒方程和能量守恒方程，分别描述如下。

质量守恒方程，也称连续性方程，可表示为：

式中：ρ为流体密度；u，v，w分别表示x，y，z三个方向的速度分量。

动量守恒方程，反映的是流体在流动过程的动量守恒的性质，针对于离心压缩机内部流动，动量守恒定律对应的控制方程为N-S 方程，湍流模型选用SST 模型，可表示为：

式中：ui、uj表示速度矢量；ui’、uj’表示速度脉冲量；P表示压力；μ表示粘性系数。

能量守恒方程，是根据能量守恒原理建立的，可表示为：

式中：cp为比热容；T为温度；k为传热系数；ST为流体内热源及由粘性作用产生的热能。

压缩机的工作总压比是用来衡量压缩机的实际运行工况，通过式（4）算得：

式中：po为压缩机出口总压，kPa；pi为压缩机入口总压，kPa。

等熵效率定义为压缩机等熵压缩功与实际压缩功之比，通过式（5）算得：

式中：hi为压缩机入口工质焓值，kJ/kg；ho为实际压缩过程的出口工质焓值，kJ/kg；hos为理论上等熵压缩的出口工质焓值，kJ/kg。

级间补气蒸气混合过程的热平衡关系式，通过式（6）算得：

式中：qm1为一级压缩机工质质量流量，kg/s；h1o为一级压缩机出口工质焓值，kJ/kg；qmG为经节流阀进入经济器的流量，kg/s；hG为经济器出口工质焓值，kJ/kg；qm2为二级压缩机工质质量流量，kg/s；h2i为二级压缩机入口工质焓值，kJ/kg。

冷却电机的换热量，通过式（7）算得：

式中：qmM为电机入口工质质量流量，kg/s；hMo为电机出口工质焓值，kJ/kg；hCo为冷凝器出口工质焓值，kJ/kg。

双级压缩系统的制冷量通过式（8）算得：

式中：qm为工质的质量流量，kg/s；q0为单位制冷量，kJ/kg；h1i为一级压缩机入口工质焓值，kJ/kg；hE为蒸发器入口工质焓值，kJ/kg。

双级压缩系统的性能系数COP 通过式（9）算得：

式中：Q0为循环系统的制冷量，kW；W1为第一级压缩机的耗功，kW；W2为第二级压缩机的耗功，kW。

3 网格及边界条件

离心压缩机作为一种旋转机械，其流道曲面多，结构复杂，并且具有周期性，为了减小计算量，所以只抽取进口导叶区域、叶轮和扩压器的单流道进行数值模拟。对导叶区域、叶轮和扩压器采用六面体结构化网格，蜗壳采用四面体非结构化网格，各流体域网格如图2 所示，同时分别对开度为-20°、0°、20°、40°的导叶区域进行网格划分。为了避免网格质量对模拟结果产生影响，需要对离心压缩机整级模型进行网格无关性验证，不同网格方案下两级压缩机的总压比如表2 所示。

图2 双级离心压缩机各流体域网格Fig.2 Two-stage centrifugal compressor each fluid domain mesh

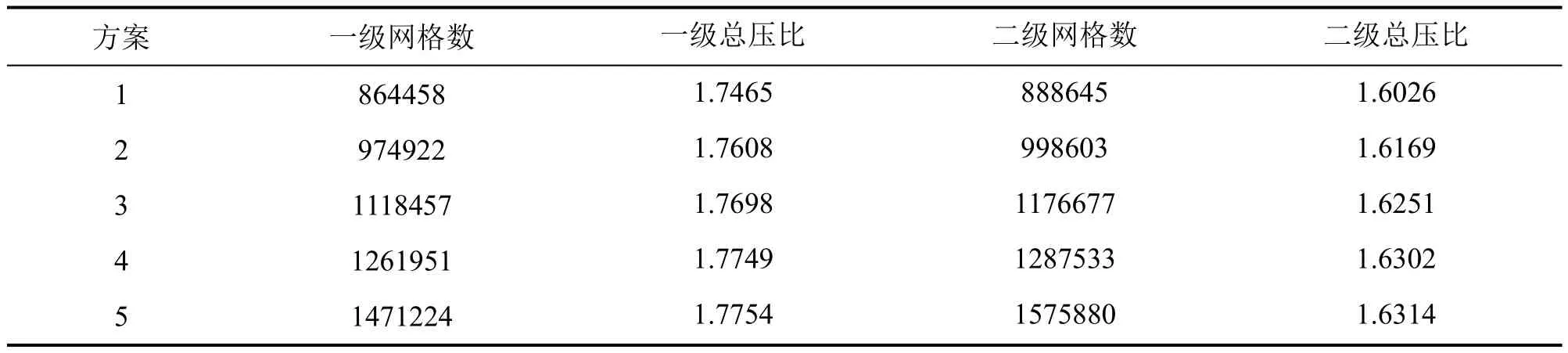
表2 网格无关性验证Table 2 Grid independence verification

从表2 可以看出，随着网格数的增加，压缩机总压比的误差逐渐减小，当网格数增加到方案4时，压缩机总压比几乎不再随网格数目的增加而增加，计算精度已满足要求，因此选择一级压缩机导叶区域、叶轮、扩压器以及蜗壳的网格总数为1261951，二级压缩机叶轮、扩压器以及蜗壳网格总数为1287533 进行计算。

本文基于压缩机实际运行工况，采用CFX 软件进行求解，设置叶轮部分为旋转计算域，进口导叶部分、扩压器和蜗壳部分为静止计算域。边界条件采用总压总温入口和流量出口，给定一级压缩机入口总压为355.78kPa，入口总温为8.5℃，压缩机转速为21000r/min，湍流模型采用SST 模型，工质为R134a，出口通过给定不同的流量来改变运行工况点，二级压缩机入口状态由一级压缩机排气和级间补气状态决定。

4 计算结果及分析

4.1 内部流场分析

图3 为不同导叶开度下沿叶高方向的流线和相对马赫数分布规律。从图3（a）可以看出，开度为0°时，相当于无进气预旋，流线非常平稳，开度为±20°时流线比较均匀，当开度上升到40°时则出现了漩涡，这是因为在导叶吸力面的叶顶处有低速流体，导致该部分流动损失增大，故此时的流线较为紊乱。从图3（b）可以看出，不同导叶开度马赫数分布明显不同，导叶开度为0°时，导叶后基本不存在流动分离，导叶开度为±20 度时，导叶后出现流动分离，前缘处出现较大的流动分离，尾缘处出现分离涡团。导叶开度为40 度时流动分离进一步加剧。导叶开度为正时叶轮进口相对马赫数减小，而开度为负时进口马赫数随开度增大而明显增大。

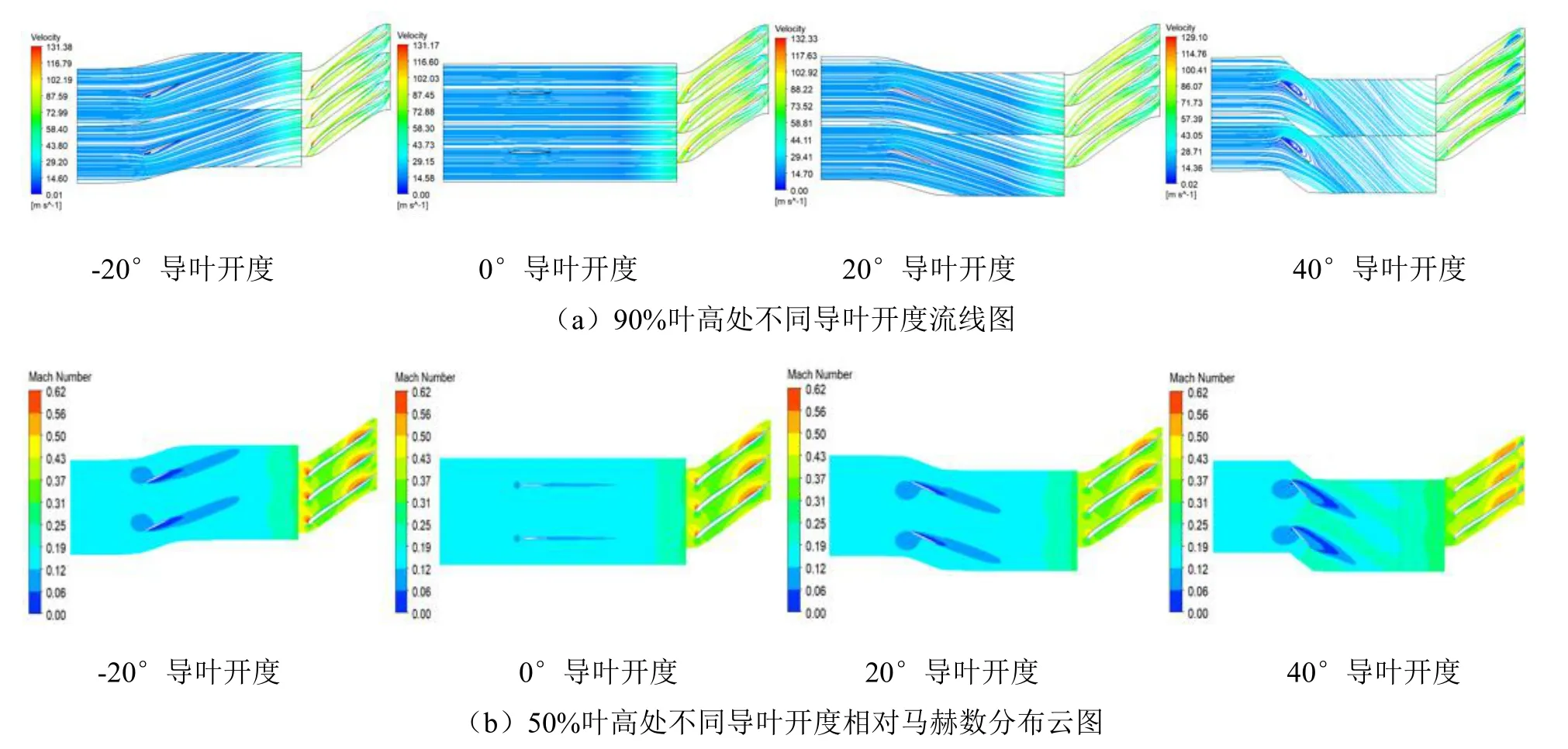
图3 沿叶高方向不同导叶开度的流线图和相对马赫数分布云图Fig.3 Flow diagram and relative Mach number distribution cloud diagram of different guide vanes openings along the blade height direction

4.2 离心压缩机性能分析

为了分析不同导叶开度下气悬浮离心压缩机的性能，在给定边界条件下分别模拟了不同导叶开度时的离心压缩机的性能，获得了两级压缩机性能变化曲线。

图4 为不同导叶开度下双级离心压缩机的流量—压比性能曲线。从图中可以看出，压缩机压比随着质量流量的增加逐渐减小，且第二级压比相比第一级较小。在近喘振区附近压比略有下降。对于一级压缩机，导叶开度为0°时，压缩机喘振时的流量约为0.96kg/s。当调整导叶开度为-20°时，喘振点流量约为1.04kg/s，相比0°时流量增大约8.3%，并向右移动。当导叶开度为20°和40°时，喘振点流量则分别约为0.90kg/s 和0.84kg/s，相比0°时流量继续变小，且分别向左移动约6.3%和12.5%。在流量相同情况下，导叶负开度会增强压缩机的做功能力，故增大了压缩机的压比，在-20°时压比平均增大了约1.3%，而导叶正开度会使压缩机的做功能力降低，在20°时压比平均减小了约1.9%，在40°时压比则平均减小了约6.6%。对于二级压缩机，由于与一级压缩机共轴且存在中间补气冷却，导致入口条件均发生变化，所以导叶开度对二级压缩机压比影响较小。从图中可以看出，在较大流量工况下，压比变化规律与一级类似，而小流量工况下受一级排气参数及补气参数的影响，各导叶开度均使压比有所降低。

图4 不同导叶开度流量-压比曲线Fig.4 Flow-pressure ratio curves for different guide vanes openings

不同导叶开度的流量—效率曲线如图5 所示，从图中可以看出，等熵效率随流量的增大先上升后下降，两级压缩机效率变化范围分别为79%～91%和54%～92%，二级压缩机效率变化幅度比一级变化幅度略大。对于一级压缩机，当导叶开度为0°时，效率最高时流量为1.96kg/s，效率最高可达90.40%。而当导叶负开度时，性能曲线上最高效率点有向大流量方向移动的趋势，相比0°时最高效率降低约1.6%，这是由于导叶负开度会增大叶尖相对马赫数，同时使叶片前缘正攻角增大，从而导致效率下降。而当导叶开度为正时，性能曲线上最高效率点的流量向小流量方向移动，20°时等熵效率相比0°时最高效率升高约0.63%，这是由于导叶正开度会使马赫数和攻角都减小，从而使效率上升。随着导叶开度的增大，最高效率点向小流量移动的幅度也随之增大，40°时等熵效率最高可达89.10%，此时的最高效率反而比0°时降低了约1.4%。对于二级压缩机，也有类似的变化规律，即导叶正开度最高效率点的流量向小流量方向移动，导叶负开度最高效率点的流量向大流量方向移动。

图5 不同导叶开度流量-效率曲线Fig.5 Flow-efficiency curves for different guide vanes openings

图6 为双级离心压缩机变导叶开度时的流量-功率曲线。从图中可以看出，双级压缩机功率随流量增加而增加，但随着压缩机流量的进一步增加，压缩机的功率开始有所下降，且二级压缩机的功率小于一级。对于一级压缩机，小流量工况时，导叶开度对压缩机功率影响较小，随着质量流量的增大，导叶开度对压缩机功率的影响越来越大。相同流量下导叶负开度时较导叶开度为0°时压缩机功率有所增大，平均增大了约4.1%，而导叶正开度时压缩机的功率则小于导叶开度为0°时的功率，且导叶开度越大功率越小。导叶开度为20°和40°时压缩机功率相比0°时平均减小了约4.1%和11.2%。对于二级压缩机同样具有相同的变化规律，小流量工况下不同导叶开度时压缩机的功率趋于一致，大流量工况下导叶负开度时压缩机功率增大，而正开度时压缩机功率减小。

图6 不同导叶开度流量-功率曲线Fig.6 Flow-power curves for different guide vanes openings

4.3 系统性能分析

为了分析导叶开度对系统性能的影响，考虑级间补气、气悬浮轴承供气、电机冷却过程，并通过CFD 方法模拟压缩机的实际排气参数及效率，计算循环系统中各个状态点的参数，从而对不同导叶开度下的系统性能进行分析。

在相同的蒸发温度、一级压缩机出口流量固定为1.96kg/s 的情况下，通过给定不同的相对中间补气量，计算得到不同导叶开度下制冷系统的COP随中间补气量的变化情况，如图7 所示。从图中可以看出，导叶负开度使系统的COP 降低，相比0°时平均降低了约2.5%，导叶正开度则升高了系统的COP，且开度越大，升高幅度越大，导叶开度为20°时相比0°时COP平均升高了约3.1%，40°相比0°时则平均升高了约9.8%。同一导叶开度下，系统的COP 随着中间补气量的增加而降低，但变化较小，相对中间补气量从2%增加到8%，系统COP 仅降低了约1.7%。

图7 不同导叶开度系统的COP 随中间补气量变化图Fig.7 COP of the system with different guide vanes openings as a function of intermediate air supply

在相同的蒸发温度、相对中间补气量情况下，压缩机出口通过给定不同的流量，计算得到不同导叶开度下制冷系统COP 随压缩机工作压比的变化规律，如图8 所示。从图中可以看出，随着工作压比的增加循环系统的COP 不断降低，当工作压比从1.6 增加到2.8 时，系统COP 降低了约47.5%。受两级压缩机效率及功耗的影响，当工作压比小于2.4 时，导叶开度为20°时系统COP 较高，较开度为0°时平均升高了约3.8%，而导叶开度为-20°时系统COP 最低，平均降低了约4.1%。随着工作压比的进一步增大，小开度时系统的COP几乎趋于一致，而导叶开度为40°时系统的COP最低。

图8 不同导叶开度系统的COP 随工作压比变化图Fig.8 COP of the system with different guide vanes openings as a function of operating pressure ratio

5 结论

本文针对带可调导叶的双级离心压缩机及制冷系统，通过CFD 的方法模拟了变导叶开度下压缩机的内部流场及运行特性，并对制冷循环系统性能进行了分析，得到如下主要结论：

利用导叶调节可以明显拓宽气悬浮制冷压缩机运行工况范围。当导叶开度为正时压缩机压比明显下降，压缩机稳定运行工况变小且向小流量方向偏移，而负开度时则与之相反。双级压缩机的等熵效率均随流量的增加呈先增大后减小的趋势，导叶正开度使压缩机最高效率点的流量向小流量工况移动。压缩机的功率随着流量的增加而增大，但大流量时功率开始减小，且导叶正开度使压缩机功率减小，而负开度则增大了压缩机功率。系统的COP随中间补气量的增加而降低，工作压比的降低使得导叶正开度时系统COP 增大。当工作压比小于2.4时，导叶开度为20°系统的COP 最高，相比0°时平均升高了约3.8%。通过导叶调节并配合转速等其他调节方式，并综合考虑压缩机及系统性能，对建立压缩机综合调控策略、提高压缩机工作效率和运行裕度具有重要意义。