基于MEA-BP 神经网络的压力传感器误差补偿算法

时 豪,范 辉,李建辰,赵润辉,李 亚

(中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

压力传感器在工业中的应用十分广泛,硅是其敏感元件的主要材料。由于半导体的固有特性对环境变化较为敏感,当外界环境发生变化时,压力传感器会产生零点漂移以及灵敏度漂移。漂移一般可分为热漂移、时间漂移、力学蠕变漂移和电源漂移。其中,热漂移是决定传感器测量的关键指标,影响其测量的精度以及稳定性,为了减少外界环境对传感器输出的影响,需要对其进行误差补偿[1]。

目前误差补偿的方法主要有硬件补偿和软件补偿2 种,其中硬件补偿由于工艺成本等因素的限制,只在特殊条件下使用[2]。随着计算机技术的广泛应用,利用计算机强大的数据处理能力结合补偿算法对传感器误差进行修正的补偿方法被广泛使用。软件补偿主要分为查表法、曲线拟合法以及人工智能法。查表法忽略了标校点的测量误差且建立查找表较为复杂,需要存储数据量很大,对传感器内存要求较高,不适用于大部分传感器。曲线拟合法如插值法、多项式拟合法和最小二乘法等[3-4]只能反映传感器的整体趋势,但比神经网络的补偿精度会有所不足。

随着人工智能技术的不断发展,压力传感器被更多地应用于航空航天、船舶及石油等温度范围广,精度要求高的使用场景。例如,用于海洋监测的压力传感器精度需达0.005% F.S;用于钻井环空压力测量的传感器精度应达0.03% F.S。最小二乘法等数值计算补偿方法已逐渐不能满足测量精度的需求[5-6],而神经网络因具有很强的非线性函数逼近和模式识别能力,在工程应用中具有良好的鲁棒性[7]。基于此,Rath 等[8]提出了用人工神经网络进行电容式压力传感器的补偿;李佳君等[9]建立了反向传播(back propagation,BP)神经网络补偿模型,对压力传感器进行温度补偿。采用BP 神经网络可对复杂难以分析的非线性系统进行建模,且输出精度高,但其初始权值以及阈值是随机选择的,容易陷入局部极小值,从而影响模型的性能。郎琦[10]采用径向基函数(radial basis function,RBF)神经网络的方法来避免陷入局部极小值,虽然RBF 神经网络的逼近速度要优于BP 神经网络,但同样精度下,RBF 需要更多的神经元个数,难以达到传感器实时性的要求。

文中以压阻式压力传感器为研究对象,采用思维进化算法(mind evolutionary algorithm,MEA)对BP 神经网络的拟合过程进行优化,搜索出更优的初始权值和阈值,防止其陷入局部最优解,采用LM(Levenberg-Marquardt)算法代替梯度下降法,从而加快BP 神经网络算法的收敛速度,提高补偿算法的可靠性,并且基于此算法建立传感器误差补偿模型,以提高压力传感器的测量精度。

1 模型建立

1.1 压力传感器补偿方法选择

分析硅压阻式压力传感器的工作原理以及所用材料可知,环境因素会影响其力敏电阻的大小,导致压力传感器在不同环境下测量结果不准确,其中温度为影响最大的因素。

针对温度对传感器的影响,可采用信息融合的方法,通过一定的算法将不同信息源信息合并,得到更可靠、更准确的信息[11]。

压阻式压力传感器包含敏感元件和温度采集单元。当施加在传感器上的压力为P时,压力传感器压力输出为Up。由于压力传感器存在温度灵敏度,若只对其进行一维标定实验,通过输入和输出特性曲线来求取被测压力值会有较大误差。P可由Up和温度采集输出值T二元函数来表示,即

针对由温度产生的误差,可采用软件补偿的方法进行修正,且成本较低。此时可将传感器的温度补偿转化为二元回归问题,对传感器产生的电信号经过整形、滤波、放大并转换为数字信号进行标定实验,分别采集不同温度和压力下的压力传感器输出电压以及温度传感器数值。

表1 为不同常用误差补偿方法优缺点对比,文中以实现高精度补偿为目标,最小二乘法及插值法在实现高精度补偿时需要建立更高阶次的多项式,当多项式阶次大于3 时,在实际工程中,传感器芯片的运算能力有限,通常不能达到实时性的要求。同样,RBF 神经网络虽能逼近任意函数,但在高精度要求时,需要建立大量隐层神经元,对硬件的计算能力同样有很高要求。文中选取BP 神经网络法进行补偿,能在满足精度同时,生成体量适中的补偿模型。该方法利用上位机建立温度特性关系,将关系式下载到传感器芯片中,获取当前时刻的压力和温度信息即可完成温度补偿。

表1 不同误差补偿算法比较Table 1 Comparison among different error compensation algorithms

1.2 BP 神经网络优化思路

BP 神经网络法是目前在拟合补偿方面较为可靠且精度较高的一种方法[12]。针对压力传感器的压力补偿,建立图1 所示拓扑结构,其中:输入层包含2 个神经元,分别对应压力传感器的输出电压以及温度;隐层设置为单层5 个神经元;输出层为1 个神经元,对应传感器实际承受的压力。

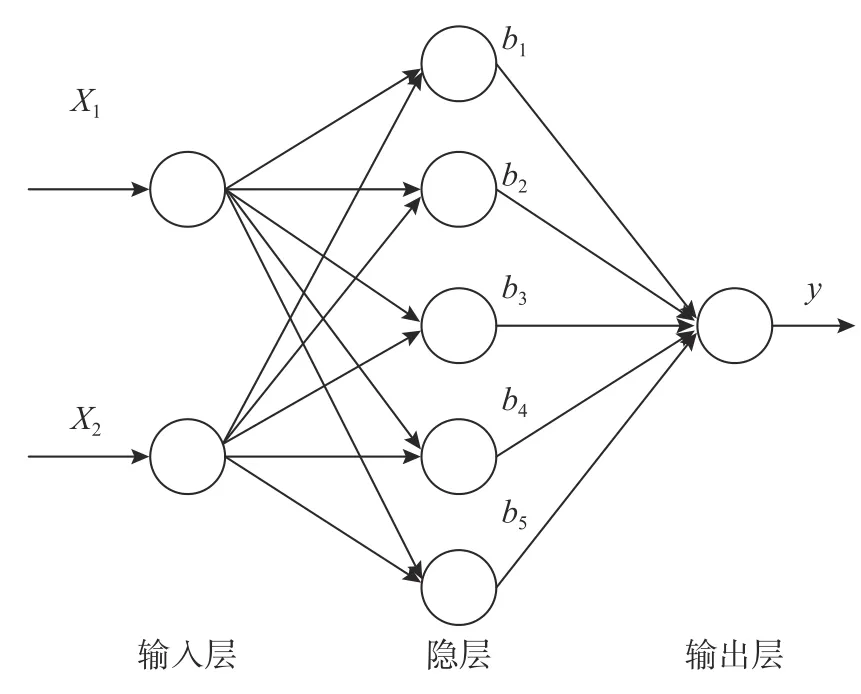
图1 BP 神经网络拓扑结构示意图Fig.1 Topology of the BP neural network

采用梯度下降的方案搜寻最优解时,负梯度方向是函数下降最快的方向。当误差函数的梯度下降为零时,达到局部极小值。如果误差函数仅有一个极小值时,找到的极小值就是全局最小值,但是误差函数通常会有多个局部极小值,则不能保证找到的解是全局最优。

采用寻找最优初值的策略,在空间中随机生成神经网络的权值和阈值,通过竞争获取最优值,作为神经网络新的初值,同时采用LM算法代替梯度下降法作为神经网络参数寻优的方法。从而降低了BP 神经网络陷入局部最优解的可能性;同时克服了BP 神经网络收敛速度慢,效率低的缺点,增加了神经网络补偿的稳定性。

1.3 基于MEA 优化的BP 神经网络模型

MEA 依靠计算机模仿人类的思维进化,并改进进化算法的缺陷。其原理与遗传算法(genetic algorithm,GA)类似,引入“收敛”和“异化”过程代替GA 中的交叉和变异2 种算子,不仅具有更快的收敛速度,而且可以大大提高解的精度[13-14]。

针对传统的BP 神经网络学习算法容易陷入局部最优解、收敛速度慢等缺点,利用MEA 算法可对BP 神经网络的初始值和阈值进行优化,确定一个更好的解的搜索空间,然后将优化后的初始值反馈给BP 神经网络,得到修正后模型的最优解。MEA-BP 神经网络流程图如图2 所示。

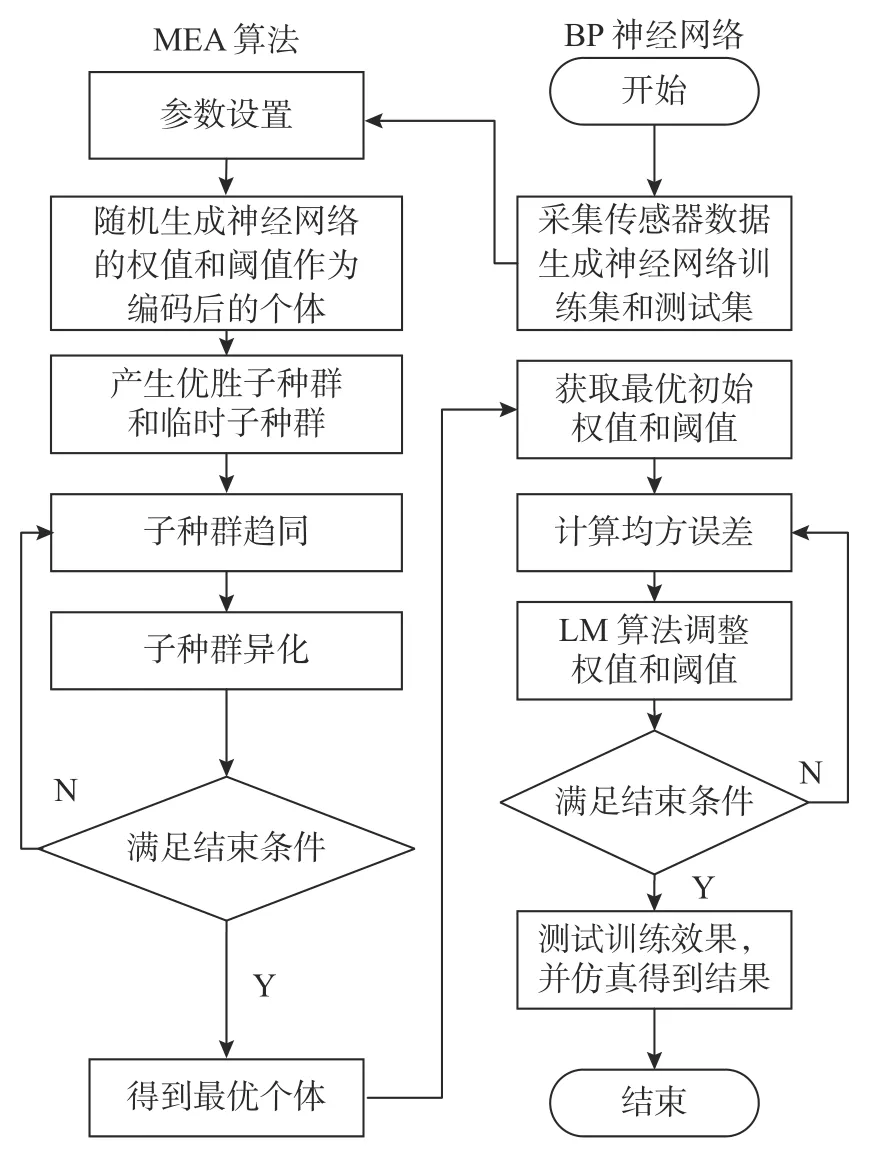
图2 MEA-BP 算法流程图Fig.2 Flow chart of the MEA-BP algorithm

MEA-BP 神经网络算法与GA-BP 神经网络算法采用相同的优化方式,但由于不同的进化机制,MEA 算法相比于GA 算法具有更高的收敛效率和全局最优概率。MEA 算法在整个解空间随机生成神经网络初始权值和阈值,将其编码后分为不同的种群,在种群内进行局部的趋同操作,在种群间进行全局范围内的异化操作,从而在全局范围内搜索到的初值中获取得分最高的解。对于有多个极小值的代价函数,经过MEA 算法的优化,可得跳出部分权值和阈值的极小值,使得初值更为接近全局最小值。

2 仿真验证

2.1 传感器数据采集

通过仿真试验采集传感器原始数据,包括训练集和测试集。试验选取图3 所示的MS5332 型号传感器,其工作温度范围为-25～70 ℃,量程为0～3 MPa。

图3 MS5332 型压阻式压力传感器Fig.3 MS5332 piezoresistive pressure sensor

利用高低温箱对传感器所处环境温度进行调整,在工作温度范围内取10 个不同温度状态,利用图4 所示压力校验仪对传感器施加压力,采集不同压力下的传感器输出电压以及温度采集设备的温度值。表2 为环境温度在26.3 ℃左右采集到的数据。

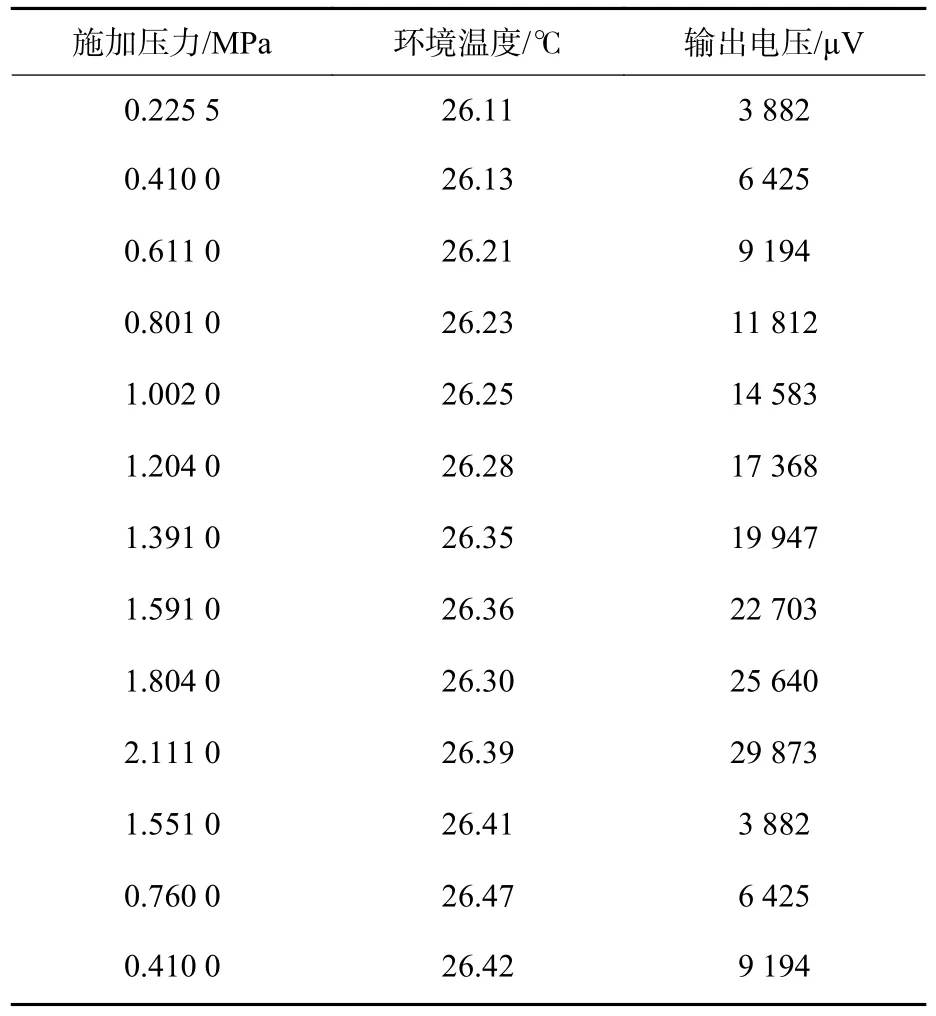
表2 压力传感器采集的数据值Table 2 The data value collected by the pressure sensor

图4 压力校验仪实物图Fig.4 Physical drawing of a pressure calibrator

图5 表现了环境温 度分别为-23、5、37 和70 ℃时,压力传感器承受压力和输出电压的线性关系。同温度下样本线性度均小于0.01%,可对其拟合数据进行插值处理,在每个温度下补至200个样本点,以提高神经网络训练样本数量,防止在训练过程中过拟合。

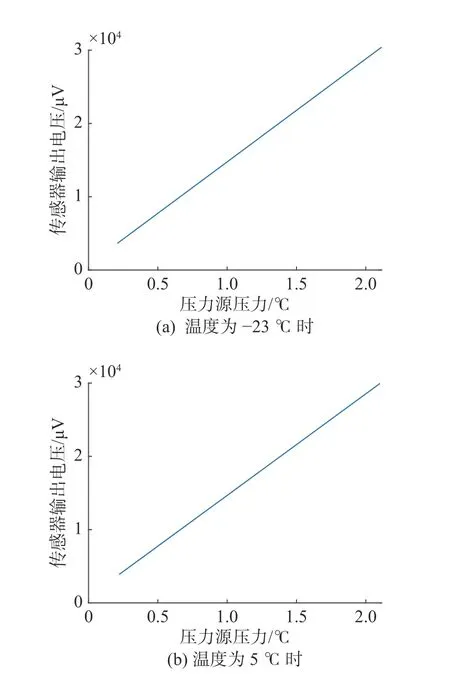
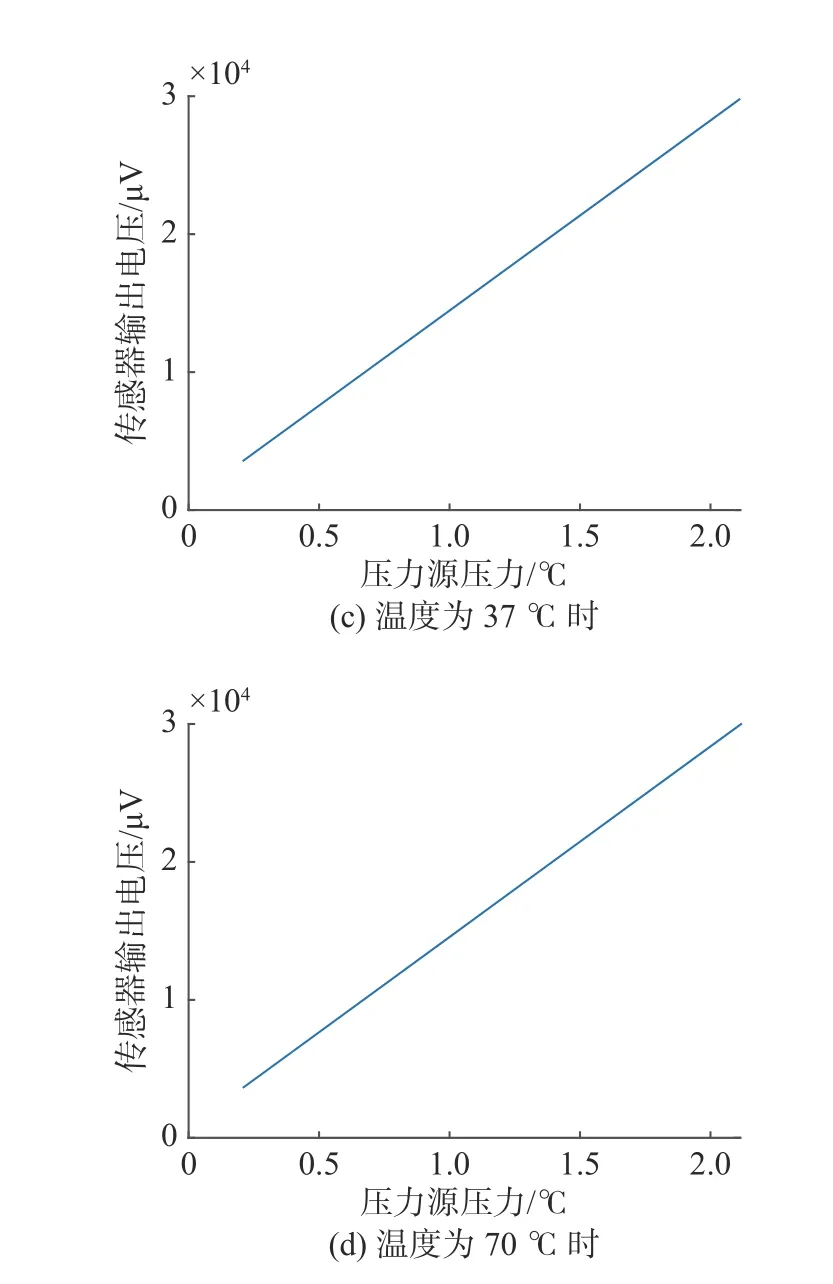
图5 不同温度下传感器承受压力与输出电压关系曲线Fig.5 Relationship curves between pressure and output voltage of sensor at different temperatures

BP 神经网络采用图1 所示结构,共有15 个权值,6 个阈值。MEA 算法编码长度为21。各温度下采集到的传感器输出数据线性度良好,可对各温度下数据进行线性拟合,以满足神经网络样本量。将各样本乱序排列,取其中1 900 组作为训练集进行训练,100 组作为验证集对神经网络模型建立效果进行评价。对上述样本分别采用BP 神经网络模型和优化后的MEA-BP 神经网络模型进行训练。

2.2 神经网络参数设置

BP 神经网络及MEA 算法参数设置如表3 所示。MEA-BP 和GA-BP 神经网络均采用与表3 相同的迭代次数、学习率以及目标误差。

表3 BP 神经网络及MEA 算法参数设置Table 3 Parameter setting of BP neural network and MEA algorithm

2.3 MEA 算法的趋同和异化

图6 表示优胜子种群和临时子种群的趋同过程,当图6(a)中优胜子种群成熟后,在全局范围内生成临时子种群,图6(b)再次进行趋同操作,可以看出成熟后的临时子种群1、2、4 的得分要高于优胜子种群中的1、2、5。此时需要进行3 次异化操作。

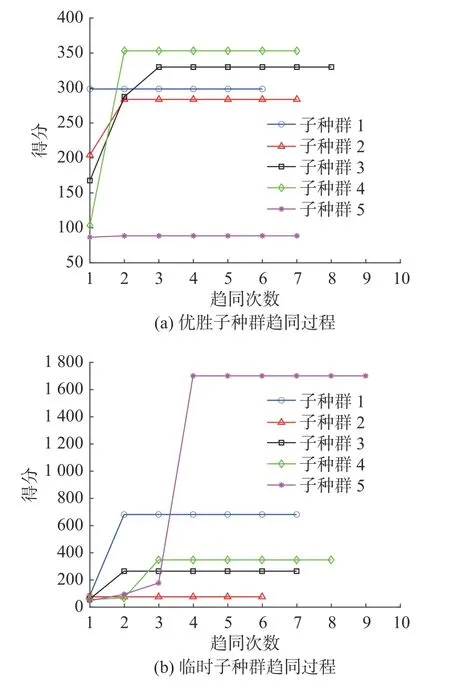
图6 MEA 算法趋同过程Fig.6 Similartaxis and dissimilation operation of MEA

再次重复趋同和异化过程,直到满足迭代次数,此时可以输出迭代获得的最佳个体,对其进行解码操作,得到初始权值和阈值。

2.4 补偿结果及误差对比分析

通过对采集到的数据归一化处理,并进行训练,采用均方根误差(root mean square error,RMSE)作为传感器补偿模型效果的评价指标,即

由于神经网络每次训练结果不同,取任意训练10 次结果进行对比,如表4 所示。

表4 不同算法10 次训练均方根误差对比Table 4 RMSE of neural network training for 10 times单位:MPa

对比10 次训练结果,原始BP 神经网络RMSE期望值1.017 3×10-3MPa,标准差5.027 8×10-4MPa。GA-BP 神经网络RMSE 期望值6.232 8×10-4MPa,标准差5.716 4×10-4MPa。采用MEA算法优化过的BP 神经网络补偿模型经过10 次训练,RMSE期望值5.223 4×10-4MPa,标准差2.458 2×10-5MPa。相比未优化的BP 神经网络和GA-BP 神经网络,MEA 算法优化后的传感器补偿模型RMSE 降低了48.7%和8.29%,标准差降为原始神经网络模型的5%和4%。

图7 为不同算法补偿后的误差曲线,3 种算法经补偿后的精度分别为0.26% F.S,0.03% F.S 和0.01% F.S。从图中可以看出,经过MEA 和GA 优化的BP 神经网络补偿精度相较于原始BP 神经网络有明显提高,改进初值的方案对避免神经网络陷入局部最优解有较好的效果。采用GA 算法优化的补偿模型虽能达到很高的精度,但在补偿时,需要对模型多次训练才能找到效果较好的结果,可靠性不如MEA 优化的补偿算法。

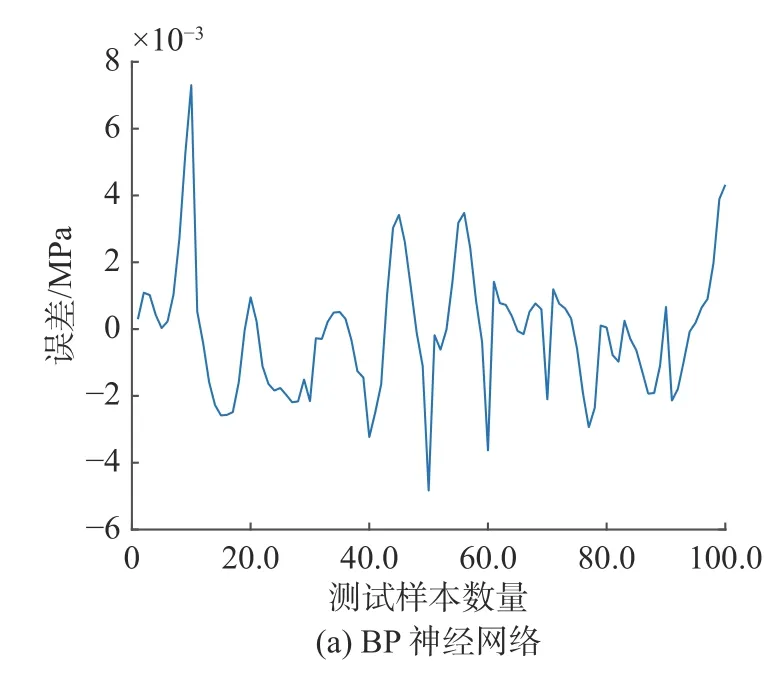
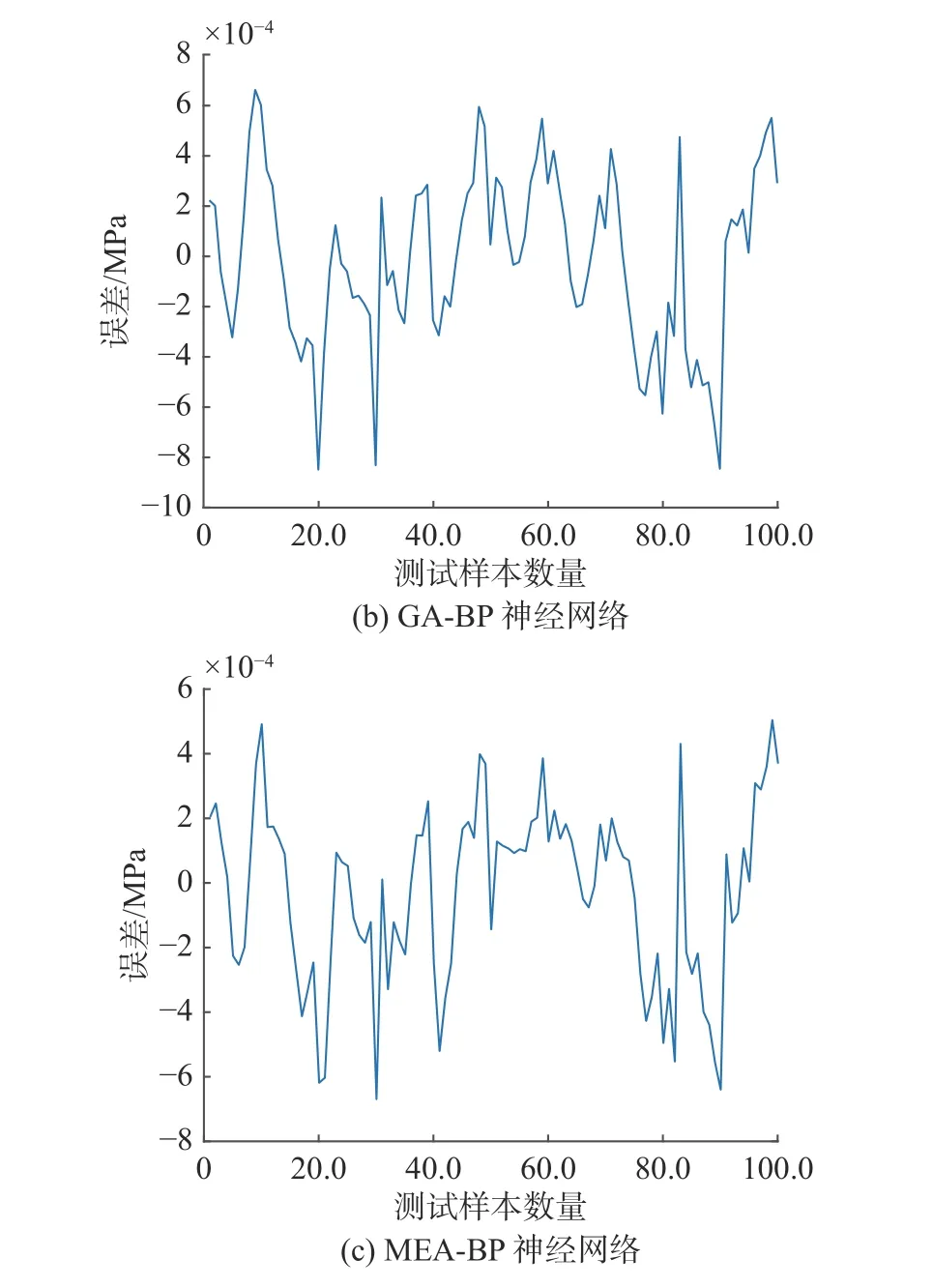
图7 不同算法补偿后的测量误差曲线Fig.7 Measurement error curves after compensation by different algorithms

3 结束语

文中基于MEA-BP 神经网络建立压阻式压力传感器温度补偿模型,并用该模型对标定数据进行补偿。与传统的BP 神经网络相比,基于MEA的BP 神经网络弥补了陷入局部最小值以及训练时间长等缺点,且在优化神经网络中的能力高于GA 算法。结果表明该模型对传感器测量效果提高较为明显,且补偿模型的可靠性较高。补偿时每次模型训练的精度都可得到保证,补偿后的测量误差可以很好地满足实际测量。文中研究是通过离线训练来生成关系表达式,传感器的性能并不能实现对误差的在线补偿,在以后的工作中,可尝试将补偿算法与传感器芯片融合,实现误差在线补偿。