基于强化学习的无人水面艇能耗最优路径规划算法

李佩娟,颜庭武,杨书涛,李 睿,杜俊峰,钱福福,刘义亭

(南京工程学院 工业中心、创新创业学院,江苏 南京,211167)

0 引言

无人水面艇可用于恶劣环境下或执行简单重复性任务,在海上石油资源勘查、海洋数据获取、反潜、反鱼雷等民用和军事领域得到了广泛应用。

无人水面艇最为基础的技术是路径规划,即规划一条从当前位置到达目标位置的路径,确保无人水面艇安全、高效地执行任务。无人水面艇长期在海洋中行驶,极易受到时变海风、海流和海浪等外部环境影响,如果在路径规划时忽略上述因素,则易偏离规划航线,增加能量损耗,甚至碰撞障碍物,无法完成任务。

多年来,针对无人水面艇路径规划问题已有诸多研究成果。文献[1]将人工势场法用于无人水面艇的路径规划,在目标点和障碍物附近设计相应势场,指引无人水面艇到达目标且避免碰撞障碍物。该方法由于计算复杂度相对较低,可用于实时路径规划,但不能避免局部最优解的情况,且不适用于动态洋流环境。文献[2]～[4]提出基于图的搜索方法(例如A*和D*),尽管能够成功避开静态障碍物,但计算复杂度随着空间维度提高呈指数级增加,并且为了保证计算效率,代价函数往往是线性的。文献[5]提出了基于双向快速随机探索树法的路径规划,给出动态步长策略以加快系统的收敛速度,但规划路径并不是最优。文献[6]和[7]针对随时间变化的洋流设计能耗代价函数,采用遗传算法求得最优路径,为了避免算法早熟,每隔20 次迭代,随机加入新的种群,但是文中假设路径沿横轴递增,造成路径搜索的不完全性。文献[8]和[9]提出基于量子粒子群算法的路径规划方法,将粒子等量约束在各个圆环内,减少了系统的计算量。文献[10]设计代价函数包含了路径长度和航行时间,利用改进的蚁群算法迭代求解非线性最优解。无人水面艇属于欠驱动系统,控制输入小于运动自由度,路径规划需要考虑其运动学特性,才能实现准确跟踪。文献[6]和[10]考虑到规划路径的长度、平滑度及能耗等信息,但忽略了无人水面艇的运动学特性,导致在满足无人水面艇路径规划的实际需求上有所欠缺。

现阶段,随着人工智能技术的发展,基于强化学习的路径规划受到越来越多的关注。与其他智能算法相比,强化学习具有不需要借助外部环境信息或预先设定规则的优点。文献[11]研究了基于强化学习的货船路径规划问题,通过建立Nomoto 船舶模型,根据障碍物、目标等信息设计相应的奖励函数,使得最终路径收敛。文献[12]和[13]研究了基于海事规则的无人水面艇路径规划问题,通过深度神经网络代替Q表,增加动作的连续性,并通过仿真验证了算法的合理性。

文献[11]和[13]主要从障碍物等方面考虑规划的有效合理性,但忽略了洋流的影响。文中基于洋流影响的无人水面艇路径规划问题,采用改进强化学习的方法,计算得到能耗最优路径。同时考虑了无人水面艇的运动学模型、航向角所受洋流和控制输入的约束等实际情况,借助B 样条法进行路径平滑。仿真验证了算法的有效性和最优性。

1 模型建立

文中研究目标是在海洋环境下,无人水面艇规划出一条从起始点到目标点的最优路径。海洋环境可以模拟为含有障碍物的洋流场。路径规划的优化准则是避免障碍物的前提下实现能耗最优。

1.1 洋流模型

在复杂的海洋环境中,洋流通常可视为多个涡流的叠加。海洋学显示涡流作用的范围从几厘米到几百千米,持续的时间从几秒到几个月。文中研究基于洋流变化缓慢的场景,并假设在整个任务过程中,洋流的强度和方向保持不变,无人水面艇借助声学多普勒流速剖面仪获得当前位置的洋流速度和方向信息。

洋流速度值vc=[vcx,vcy]的数学表达式[14]为

式中:vcx,vcy分别为洋流水平和垂直方向的速度值;d为当前点[x,y]到涡流中心点[x0,y0]的距离;Γ,σ分别为涡流的强度和涡流作用半径。

1.2 无人水面艇运动学模型

建立六自由度无人水面艇模型,其状态空间表达式为

式中:x,y,z表示在地球坐标系下的位置;f,θ,φ表示欧拉角;u,v,w,p,q,r表示载体坐标系下的线速度和角速度。

考虑到无人水面艇垂直方向上的位置或姿态变化较为缓慢且数值较小,可忽略参数z,f,θ,v,w,p,q。状态空间参数的减少有利于减少系统的计算量,因此,无人水面艇的运动学模型可以简化为两自由度的水平运动,即

式中:p,v,φ分别表示无人水面艇的位置、速度、航向角信息;vs和 φs分别为无人水面艇在静水中的速度值和航向角值;vc和 φc分别为洋流的速度值和航向角值;ui为控制输入。图1 给出无人水面艇和洋流的速度和航向角的矢量图。

图1 无人水面艇和洋流的速度矢量示意图Fig.1 Velocity vector schematic of USV and ocean current

2 强化学习方法

强化学习与其他机器学习最大的区别是无需监督信号,而是通过智能体与环境不断交互,以奖励值最大为目标。智能体、环境、状态、动作、策略和动作价值函数是强化学习最重要的组成部分。图2 展示了强化学习的基本框架。

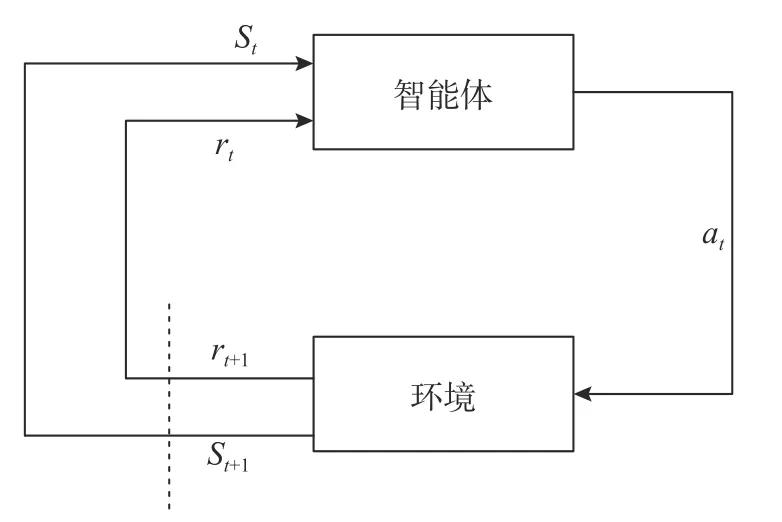
图2 强化学习基本框架Fig.2 Basic framework of reinforcement learning

智能体在状态St下采取动作at,环境给出相应的奖励rt+1,智能体的状态转化为St+1,不断重复上述过程,直到策略 π收敛。其中,智能体的状态集S={s1,s2,···,sn},智能体动作集A={a1,a2,···,an},奖励函数R={r1,r2,···,rn}。

文中采用强化学习中常用的Q-learning 算法进行路径规划。在Q-learning 算法中,动作价值函数Q(s,a)是当前状态到目标状态期望奖励的叠加。强化学习可表示为寻求最优的策略,即通过动作价值函数Q(s,a)在每一个状态选择最好的动作。

Q(s,a)更新公式为

式中:r为状态s采取动作a获得的奖励;s′和a′分别为下一步的状态和动作;α为学习率;γ为折旧率。

为加快Q-learning 算法的收敛速度,引入迹的思想,能够记录状态被访问的次数,在更新前一时刻的状态值函数时,对以往状态值函数进行更新,即Q(λ)算法。其更新公式为

在Q(s,a)更新过程中,动作选择使用greedyε贪婪策略,即

式中:定常参数I和E分别为当前迭代数和总迭代数;ε∈[0,1]为当前策略的贪婪值。

ε贪婪策略的提出权衡了探索和利用2 种方式。若随机数p∈[ε,1],系统进行探索,随机选择动作;若随机数p∈[0,ε],系统贪婪选择当前状态下最大价值的动作。训练的初始阶段,由于对环境的完全未知,系统借助较小的 ε贪婪值,大概率随机选择动作,探索更多的动作,避免收敛到局部最优解。但随着迭代次数的增加,系统对于环境逐渐熟悉,ε值也随之增加,系统大概率选择当前价值最大的动作,避免没有价值的探索,加快系统的收敛速度。

Q(λ)算法的伪代码如下:

3 路径规划算法

针对基于传统强化学习的路径规划问题,规划的路径存在直角或大角度,设计符合无人水面艇运动学特性的动作集和状态集。通过设计合理的函数,使得路径能耗最优。

3.1 动作集

考虑到无人艇不可能出现横向或短时间内大角度移动情况,因此其运动学模型中,舵角的输入必须限制在一定的范围内,即ui∈[-36°,36°]。对舵角采用5 个离散化动作,即[-36°,-18°,0°,18°,36°],如图3 所示。

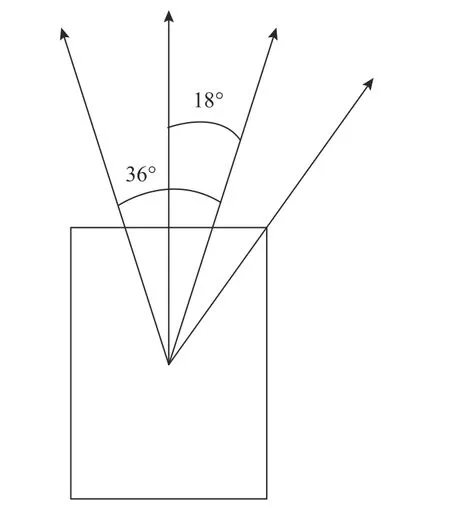
图3 无人水面艇舵角的离散动作Fig.3 Discrete action of the rudder angle of USV

3.2 状态集

无人水面艇的运动状态与航向角、横轴、纵轴坐标相关,表示为[(x1,y1,φ1),(x2,y2,φ2),···,(xn,yn,φn)],其中:x,y表示横轴和纵轴的坐标;φ表示航向角。为简化计算量,提高算法的运行效率,将航向角划分为20 个区域,每个区域分辨率为18°,航向角的编号如图4 所示。

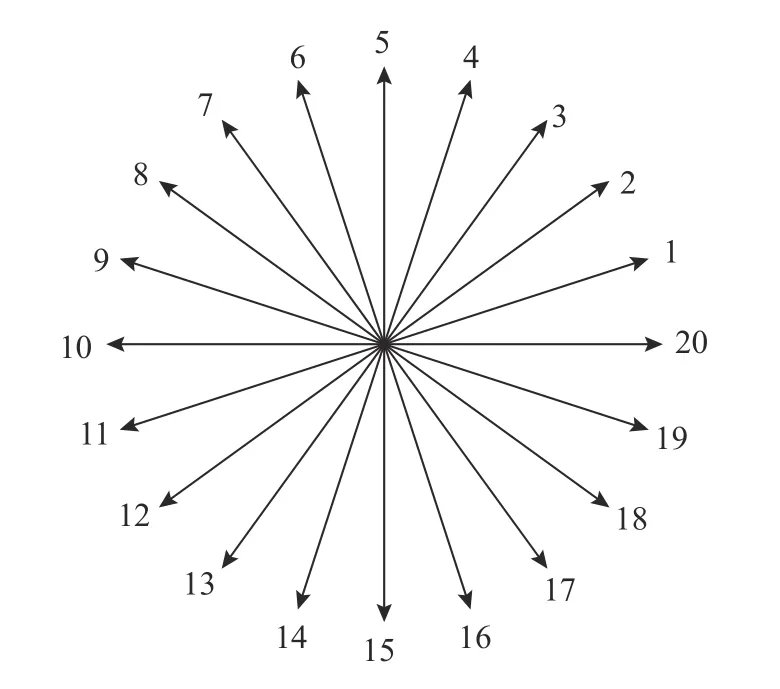
图4 无人水面艇航向角编号Fig.4 Numbers of USV heading angles

3.3 奖励函数

奖励函数定义为评估当前状态下采取某一动作的价值。文中研究目标是无人船在避免障碍物的前提下,以能耗最优的方式达到目标点。因此,奖励函数设计为防碰撞奖励f1和能耗奖励f2两部分。

路径规划首先要确保无人水面艇不与障碍物发生碰撞,当水面艇与障碍物距离小于安全半径时,将受到惩罚,其他情况为0。

防碰撞奖励函数设计为

式中,d和rsafe分别为无人水面艇与最近障碍物的距离和安全半径。

假设无人水面艇推进功率恒定,等价为无人水面艇在静水速度vs恒定,能耗最优的路径即为在洋流干扰下,最短时间内从初始位置达到目标位置的路径。

无人水面艇的静水速度vs,洋流的速度vc(为φ 和 φc的合成速度)以及洋流速度与水平面夹角均已知,相对关系如图1 所示。

根据三角函数分别求得无人水面艇合成速度v以及静水速度与水平方向夹角φs

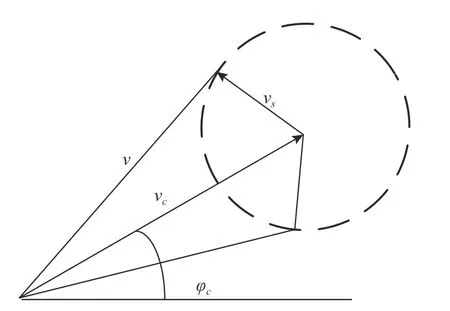
图5 洋流影响下无人水面艇航向角取值范围Fig.5 Range of the heading angle of USV under the influence of ocean current

因此,能耗奖励设计为

式中:dgoal为无人水面艇与目标的距离;t为单步的动作时间;r0为路径收敛时无人水面艇与目标的最短距离。

能耗奖励函数设计为[8-10]

式中,Ki-1和Ki为当前路径中邻近的两点。

假设无人水面艇速度均大于洋流速度得到该函数节点,忽略存在洋流速度大于无人水面艇的速度,导致路径上的点根本无法到达的情况。

因此,算法的总奖励函数R=f1+f2。此后,每一步实时更新无人水面艇的状态和洋流信息,即

3.4 B 样条法

洋流、控制输入的离散性等因素会影响无人水面艇规划路径的平滑度和曲率,常用的平滑算法有B 样条法和随机梯度法[15]等。其中,随机梯度法需要设计包含相邻路径点距离和角度信息的平滑代价函数,计算量大,百次迭代才能收敛;B 样条法为多项式阶拟合,阶次较低,可以对曲线进行局部修正。所以,文中采用B 样条法进行路径平滑。

B 样条由分段多项式组成,具体数学表达式

式中:pi为控制节点;Ni,or为样条的基函数,决定了样条的平滑程度,下标or代表阶数。

式中:*代表卷积;f为步长。

3.5 算法流程

基于能耗最优的路径规划算法具体步骤如下:

1)设定初始位置、目标位置、初始化算法参数以及洋流等外部环境模型;

2)开始第i次迭代;

3)执行式(7)贪婪策略,选择动作;

4)执行式(11)～(15),计算奖励r以及无人水面艇下一步状态s′;

5)执行式(6),更新动作价值函数,将无人水面艇下一步s′赋值给当前状态;

6)若无人艇到达目标距离dgoal≤r0,结束当前迭代,跳转至步骤2)且i=i+1,否则执行步骤3);

7)若路径收敛或达到最大迭代次数则执行步骤8);

8)执行式(16),使用B 样条法进行路径平滑。

算法的流程框图见图6。

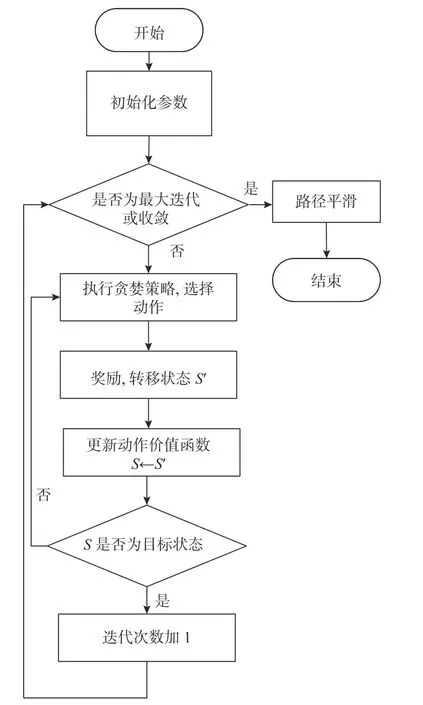
图6 基于能耗最优的路径规划算法流程图Fig.6 Flow chart of energy-optimal path planning algorithm

4 仿真验证

采用1.1 节描述的洋流场,在400 m×400 m 海洋环境中随机产生10 个涡流中心点,涡流强度Γ和涡流作用半径 σ分别设置为100 m2/s 和10 m。无人水面艇在静水中的速度设置为2 m/s,单步动作时间为10 s，无人水面艇初始状态和目标状态分别(45 m,75 m,0)和(345 m,305 m,(π/2)rad)。洋流场描述矢量图如图7 所示,图中,绿色米子型标记为涡流中心点,蓝色和红色圈代表无人水面艇的起始位置和目标位置。

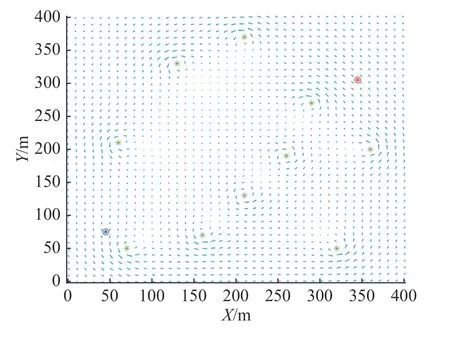
图7 洋流场矢量图Fig.7 Ocean current vector map

强化学习参数设计如下:设定环境的长、宽、角度分辨率分别为10 m,10 m,18°,学习率α=0.3,折旧因子γ=0.9,初始探索系数ε0=0.5,最大迭代次数20 000。单步结束的条件为无人水面艇到达指定范围内或者碰到边界,总的迭代终止条件为规划路径收敛,即连续10 次训练迭代次数的方差小于0.2。若达到最大迭代步数还未收敛,则视为当前训练失败。

情况1 外部环境仅受洋流影响

图8 为基于洋流约束的无人水面艇仿真路径。图中,无人水面艇沿着洋流的方向顺流而行,文中算法的航行花费时间为183 s,节约了大量能量。无人水面艇沿虚线虽能直达目标位置,但大都逆流而行,需浪费大量能量克服洋流的影响,最终航行花费时间为224 s,不利于无人水面艇长时间执行任务。文中算法规划路径符合无人水面艇的运动学约束,且较为平滑,不存在较大的转向角。传统Q-learning 算法和粒子群算法由于存在横向移动,出现较大转向角,不利于无人水面艇的实际运动。

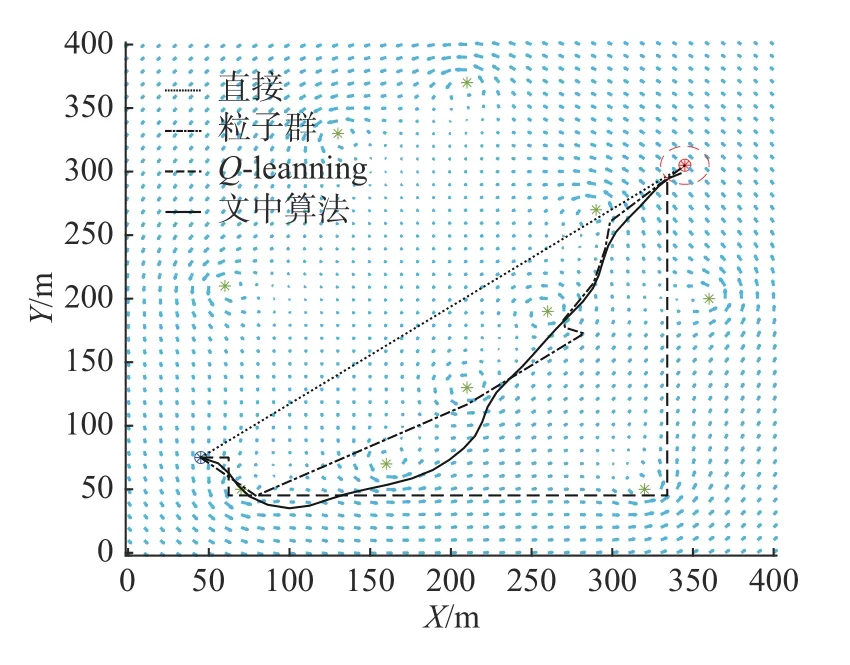
图8 基于洋流约束的无人水面艇仿真路径Fig.8 Simulation paths of USV based on ocean current constraints

情况2 外部环境受洋流和障碍物影响

为了验证算法的避障效果,在图7 规划路径的基础上添加4 个不同半径的障碍物,如图9 所示。从图中可以看出,传统的Q-learning 算法和粒子群算法在障碍物附近出现了大转折角且航行时间最长,而文中算法由于避免障碍物等原因,存在部分逆流状态,导致航行花费时间较情况1 长,但总的航行时间在3 个算法中最短。

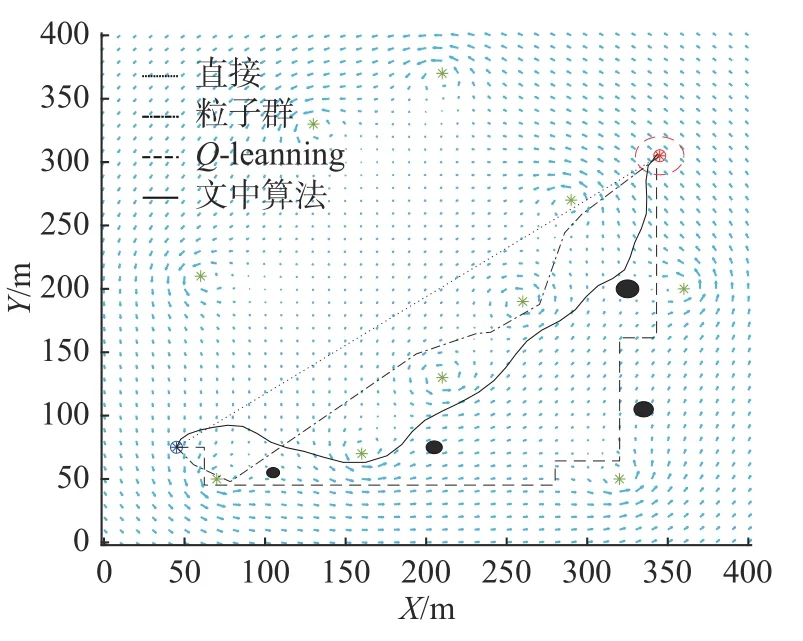
图9 基于洋流和障碍物约束的无人水面艇仿真路径Fig.9 Simulation paths of USV based on obstacles and ocean current constraints

表1 给出了2 种情况下各算法的仿真结果。

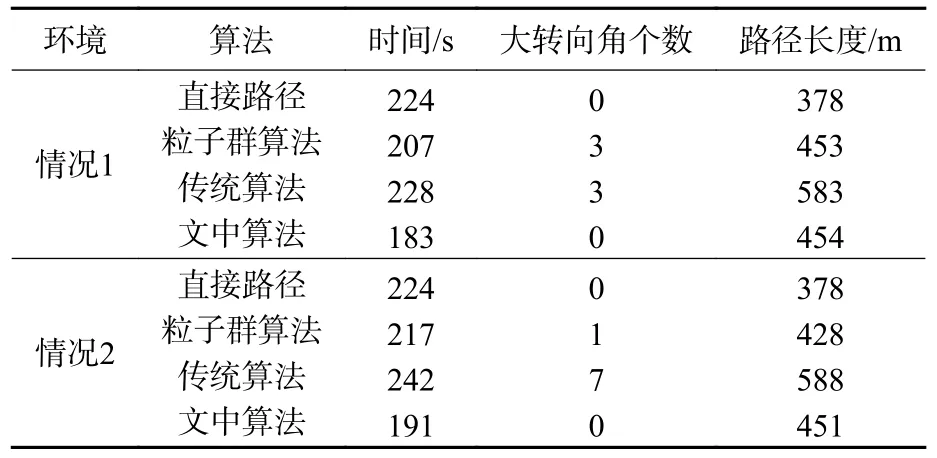
表1 仿真结果对比Table 1 Comparison of simulation results

5 结束语

针对无人水面艇海上路径规划问题,讨论了海上洋流外部干扰对路径的影响,设计了一种基于能耗最优的强化学习算法。利用无人水面艇的运动学模型和洋流模型,根据无人水面艇当前位置和航向信息,判断下一状态是否可达,设计相应的奖励函数。通过2 种环境下的仿真验证表明,传统的Q-learning 算法和粒子群算法随着障碍物增加,出现大量的转折角,不利于无人水面艇实际运动;为了减少计算量和加快计算速度,文中研究无人水面艇的控制输入为离散模式,并且优化符合海事规则的奖励函数,该方法能够规划出一条平滑的路径,并且顺着洋流方向运动,能耗最优。

结合研究进展,后续将在实际海试环境下优化无人水面艇运动学模型,并对洋流模型和强化学习算法进行试验验证。