考虑时延约束的UUV 密集集群自适应聚集控制方法
2023-05-19梁洪涛康凤举
梁洪涛 ,康凤举
(1.陕西师范大学 物理学与信息技术学院,陕西 西安,710119;2.西北工业大学 航海学院,陕西 西安,710072)
0 引言
无人水下航行器(unmanned undersea vehicle,UUV)密集集群是一种由大规模数量的智能个体组成,通过舰艇发射或岸基布放,可长时间在水下自主航行的智能无人系统[1],其以低成本、小型化、大规模和高密度等独特优势区别于个体数量有限的UUV 编队[2],可执行海洋环境探测、水下目标围捕、近海港口封锁等各类枯燥、恶劣和危险任务,被视为海洋工程领域的一种颠覆性技术[1,3]。但由于海洋环境复杂、动态和不可控,加之微小型个体感知、计算、通信和运动空间受限,精确的UUV密集集群聚集控制异常困难。
为了解决集群聚集控制问题,领航跟随、虚拟结构、势场函数以及行为控制等方法相继被提出[2,4],但这些方法都存在一定局限性:领航跟随结构容易陷入单点失败;虚拟结构方法需要获取全局信息;势场函数法存在局部锁死;行为控制法精确的数学模型难以建立。显然,上述方法很难有效解决UUV 密集集群聚集控制[1-5],难点在于:1)近邻信息获取的不完整性;2)极易触发雪崩碰撞和分裂;3)时延约束的不确定性。
受生物集群聚集、交会和跟随等自然现象启发,自组织协同控制方法成为集群控制研究的重点[6],其本质是通过个体间局部交互实现协调一致的运动,并利用长距吸引/短距排斥避免集群发生碰撞和分裂。早期,以Boids、Vicsek、Couzin 及其变结构模型为主的固定距离或数量交互的控制方法主要依据避碰-结对-聚集行为,采用速度平均机制对智能体感知范围内所有个体进行交互,这为一致性控制方法的提出奠定了理论基础[7]。Jadbabaie 等[8]更是基于非负矩阵理论对多智能体一致性问题首次给出了严格的数学证明;Morteza等[9]研究了鲁棒一致性的欠驱动水面船运动控制。然而这些方法对全局拓扑结构依赖性较高,限制了其在通信距离受限的微小型UUV 中的应用。
随着全球导航定位系统、高精度摄像机和声呐成像等观测技术被用于生物集群运动的重构和反演,选择性交互和注意力导引等交互模式相继被发现且被实证。例如,Ling 等[10]对寒鸭群观测发现,个体在身体一侧采用一对一配对交互,而另一侧采用拓扑交互,这种两侧不同交互方式可减少飞行能量消耗。Ariana 等[11]重建鱼群感知视场时发现,突然加速、转向等运动差异是最为显著的视觉注意力特征。上述仿生机理不但揭示了集群行为演化的产生机理,也为自组织集群控制提供了新的视角[12-14]。段海滨团队[12]研究了配对交互行为启发的无人机集群编队控制。刘明雍团队[13]研究了基于邻域跟随的集群系统分群控制。Liang等[14]研究了考虑视觉注意力机制的UUV 集群控制一致性算法。值得注意的是,上述工作没有考虑个体通信时延问题。
由于水下环境复杂、动态、不可控,时延现象在信息交互过程中必然存在[15],前面所讨论的各类集群控制研究中,均假设个体对周围邻居位置信息的获取是实时的,未考虑个体或传输介质物理特性而导致的通信时延[1,5,8-9,12-14]。但从工程应用角度,时延阻碍了近邻运动信息获取的实时性,甚至会恶化控制性能[16]。杨盼盼等[17]研究水声通信时延条件下的AUV 集群分群控制,但缺少对集群聚集控制的分析;Yan 等[18]研究了时变时延对多UUV 编队一致性的影响规律,但其结果是基于有向拓扑。显然,UUV 密集集群自组织聚集运动中的时延分析有待进一步深入研究。
基于以上讨论,针对UUV 密集集群控制问题,提出一种考虑时延约束的自适应聚集控制方法。受仿生交互启发,优化个体近邻数量和空间分布,建立集群结队交互模型并结合一致性协议、势场函数模型和外界扰动观测器,设计考虑时延约束的UUV 密集集群聚集控制器,保证集群避碰和连通性保持。定理和仿真结果验证了方法稳定性和有效性。
1 问题描述
考虑UUV 密集集群规模为N且每个个体仅有前进、横漂、艏摇3 个自由度,第i个UUV 水平面的非线性动力学和运动学模型为
式中:ηi=∈R3为UUV 在惯性坐标系下位置(xi,yi)和航向ψi∈[0,2π);νi=[ui,vi,ri]T∈R3为UUV 在附体坐标系下的前进速度ui、横漂速度vi及艏遥角速度ri;wi=[wui,wvi,wri]T∈R3为洋流扰动;τi=[τui,τvi,τri]T∈R3为系统输入;J(ψi)∈R3×3为旋转矩阵;Mi∈R3×3为惯量矩阵;Ci∈R3×3为科里奥利和向心力矩阵;Di∈R3×3为非线性阻尼矩阵,具体形式如下:
式中:m11i=mi-Xu˙i,m22i=mi-Yv˙i和m33i=Izi-Nr˙i为附加质量;mi>0为UUV 质量;Izi为转动惯量;d11(ui)=-Xui-X|ui|ui|ui|;d22(vi)=-Yvi-Y|vi|vi|vi|;d33(ri)=-Nri-N|ri|ri|ri|;X(·),Y(·),N(·)为粘性流体水动力系数。
为便于控制律设计,根据文献[19]的状态反馈线性化技术,将UUV 非线性模型(1)转化为2 阶积分系统。定义第i个UUV 的位置pi∈R3、速度qi∈R3及其控制输入ui∈R3,可得
假设3:控制输入ui有界,并满足|ui|≤ui,max<∞。
假设4:考虑水下通信时变时延 τ有界,即存在正数 τ*并满足0≤τ≤τ*。
控制目标:在满足假设1~4 的情况下,对于模型(6),设计UUV 密集集群聚集控制方法,确保集群避碰和连通性保持,并保证所有闭环信号达到全局稳定,数学描述为
式中:Ri为最大通信距离;Di为最小避碰距离。
利用无向连通图G(V,E)表示UUV 密集集群的通信拓扑关系,其中集合V={v1,v2,···,vN}表示UUV 个体,集合E={(vi,vj)∈V×V}表示个体之间的通信关系。A=[aij]∈RN×N表示集群中个体间的连接矩阵,满足(vi,vj)∈V×V则aij=1反之aij=0。考虑个体i的通信距离为Ri,则其邻居为Ni={j|d(ij)≤Ri,j={1,2,···,N},i≠j},d(ij)表示个体i和j的欧式距离。
2 视觉引导的局部交互建模
相关研究表明,个体即时交互对象选择及其分布规律对集群产生至关重要,决定着集群内部信息传播效率和环境适应性[6,20]。一方面,交互数量需要维持有限数量的交互密度,如果数量较少则不利于信息传播,反之数量较多则会“稀释”有效信息。另一方面,空间分布有利于个体获取均匀信息以更好响应集群外部刺激,防止某些空间信息“堆积”而另外某些空间出现信息“空白”。为此,文中考虑UUV 有限视野物理特点,设计视觉引导的自适应近邻结对交互模型。
2.1 有限视野的邻居优化选择策略
假设第i个UUV 的航向角 ψi,视觉盲区 φi,通信半径Ri,避碰距离Di,将有限视野2π-φi从左视场边界开始顺时针等分为Hi个扇面ϖiι=(2π-φi)/Hi,ι=1,2,···,Hi,如图1 所示。
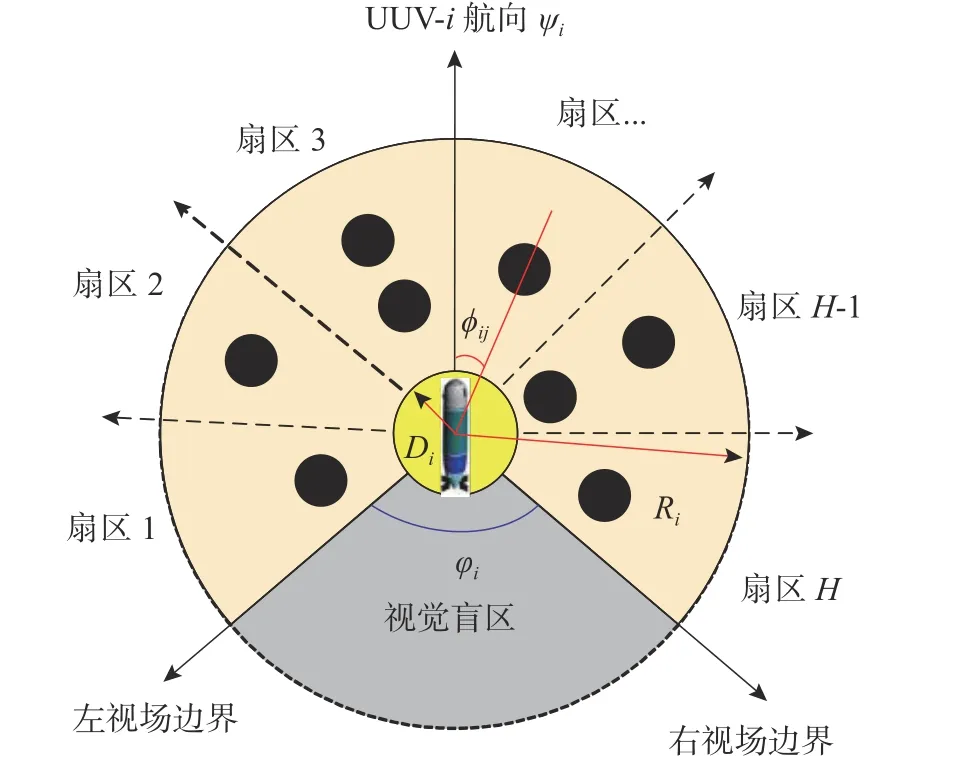
图1 有限视野的邻居选择模型Fig.1 Neighbor selection model with limited view field
第ι个扇面内的近邻集合为
式中,ϕij为第i个UUV 观测到第j个UUV 的视角。
选择第i个扇面内距离最近的个体为
式中,dij=Di≤||pi(t)-pj(t)||≤Ri。
近邻选择模型从近邻数量和空间分布2 个角度优化个体交互数量,不同于视觉引导的固定近邻数量[20]。
2.2 自适应近邻结对交互模型
根据式(12)中个体最优的近邻集合Ni,设计自适应结对交互模型,其中个体依据交互强度和有序度阈值参数自适应在单近邻模型和多近邻模型之间切换。
交互强度参数γij决定于位置 ℓij(t)、速度 νij(t)和视差耦合信息 θij,如图2 所示,定义
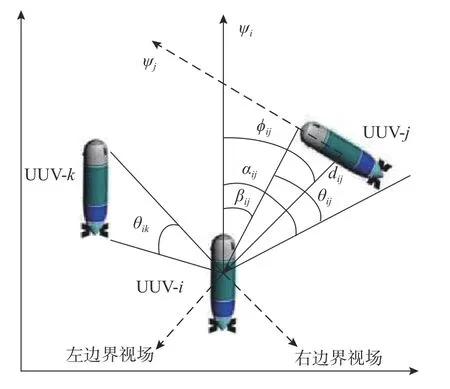
图2 自适应近邻结对交互模型Fig.2 Adaptive neighbor pair interaction model
式中,aij>0,bij>0和cij>0分别表示位置、速度和视差调节参数及其范围。
定义位置耦合参数 ℓij(t)=1/(1+|ρij|2),其中
式中:Di为避碰距离;ρij随距离增大而逐渐减小。
定义速度耦合参数
式中,Δψij=ψj-ψi为航向角差。θij越大表示个体j对个体i的威胁越大。
为增强集群环境鲁棒性,设计有序度阈值参数对集群结对行为进行自适应控制,其定义为
式中:δi>0为控制参数;Θ(qi)表示集群运动序参量
基于文献[14],结合式(13)和(17),建立自适应近邻结对交互模型
如果γij<χi,个体i采用多近邻跟随模型与其近邻集合所有个体进行结对跟随;反之γij≥χi,个体i则采用单近邻跟随模型与交互强度最大的个体j进行结对跟随。
3 集群控制算法设计
设计第i个UUV 运动模型的控制律为
对于连通性保持而言,引力势场函数ε(dij)及其功能函数Λ(dij)为
式中:kp1>0;kp2>0。
式中,kq>0。
式中:kf1>0;kf2>0。
式中:q0为全局速度;kv>0。
式中:ρ(t)∈R3为观测器辅助变量;K0=∈R3为整定矩阵。由于扰动观测器是基于UUV 非线性动力学模型,故给出稳定性证明。
证明:构造李亚普若夫函数
结合式(32)对函数(31)关于时间求导
基于假设1,存在
由式(34)可知观测误差信息有界稳定,且满足
4 时延约束的集群控制方法
考虑定常通信时延 τij=τji和γij<χi,集群控制律设计为
考虑γij≥χi,则集群控制律为
定理2:基于UUV 模型式(6)和假设1~4,考虑由于N个UUV 组成的集群且通信时延τij=τji,如果初始通信拓扑图G(V,E)连通且初始状态E0=E(p(0),q(0))属于LaSalle 不变原理集,满足参数kq=1,1≥kf1>0,kf2>0,kv>0,则集群控制律式(38)可实现:1)个体速度趋于一致性,2)集群不会发生碰撞和分裂。
证明:选取正半定Lyapunov 能量函数
对式(39)关于时间求导
结合集群控制律式(38),存在
根据连接矩阵和势场函数 Λij对称性,有
且存在
将式(41)和式(43)代入式(40),可得
进一步,结论2)采用反正法。设时间t=t1>0,个体k和个体l发生碰撞,如||pl(t1)-pk(t1)||≤D,对于t>0,则存在势场函数
式中,E0=Λij(||pl(t1)-pk(t1)||)。
由于总势场函数单调递减,存在E(pl(t1))≤E0。该结论与不变集矛盾,故在满足时间t>t1,集群不会发生碰撞。同时,假设集群拓扑图G(t)在时间tk切换,k=1,2,···,且在时间间隔[tk-1,tk]内保持不变。由于=∞,则存在
式(46)表明在t1之前没有连通图边丢失且在切换时刻t1没有发生边增加。类似地,在时间间隔[tk-1,tk]势场能量满足
集群没有发生分裂。结论1)和2)证毕。
5 仿真分析
仿真环境为Intel(R)Core™i7 CPU 3.20 GHz计算机,采用MATLAB 和C++平台。UUV 密集集群规模N=50,UUV 动力学模型参考文献[3]。个体初始位置在保证初始连通性的情况下在20 m×20 m 随机选取,且初始航行和速度分布在区间[-π,π]和[0,10] m/s,通信时延τij=τji=0.1 s。其他控制参数为φi=[-π/6,π/6],Hi=8,Ri=6.5,Di=0.3,aij=bij=cij=1.2,K0=diag[5,5,5],δi=5,Δt=0.05 s,kq=1,kf1=0.5,kf2=3,kv=20。集群期望速度q0=[4,3]m/s。仿真结果如图3~图8 所示。

图3 UUV 集群初始状态(t=0 s)Fig.3 Initial state of UUV swarm (t=0 s)
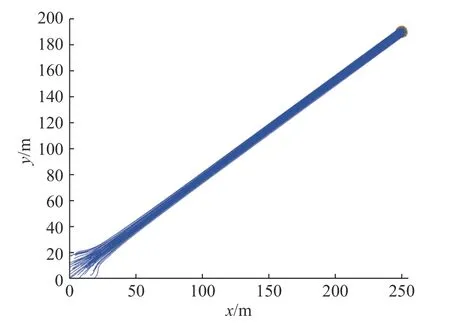
图4 UUV 集群运动轨迹Fig.4 Trajectory of UUV swarm
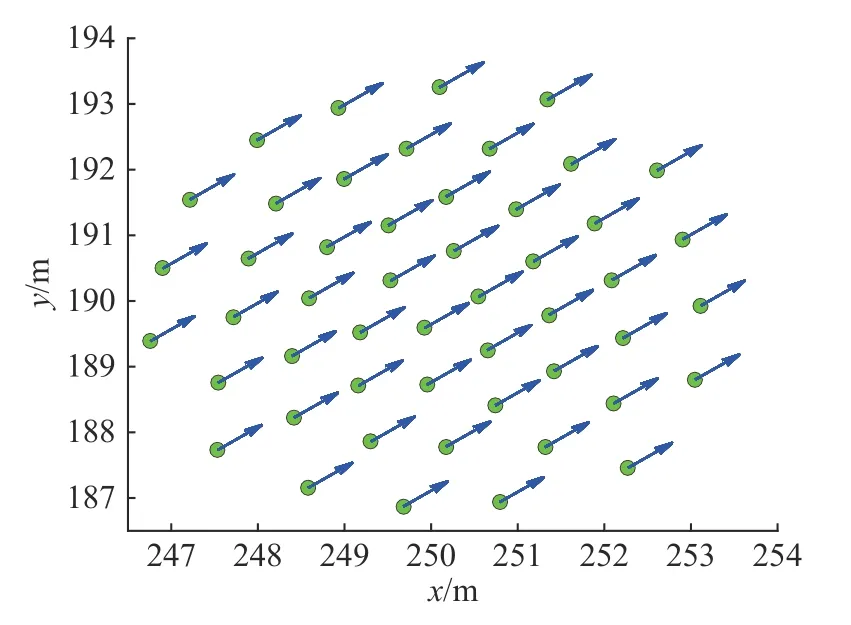
图5 UUV 集群最终状态(t=60 s)Fig.5 Final state of UUV swarm (t=60 s)

图6 UUV 集群个体间距Fig.6 Individual distances of UUV swarm
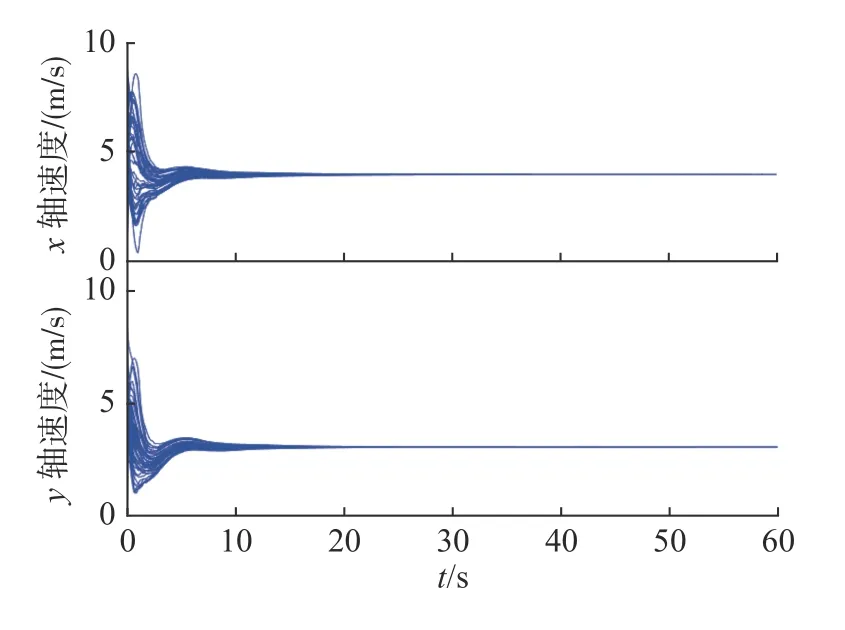
图7 UUV 集群速度曲线Fig.7 Velocity curves of UUV swarm
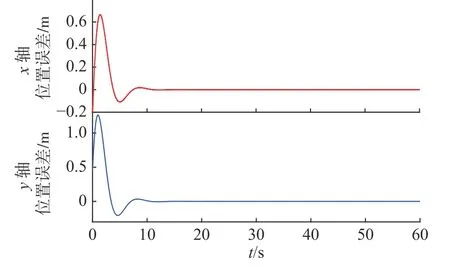
图8 UUV 集群平均位置误差Fig.8 Mean position errors of UUV swarm
从图3 可以看出,t=0 s 随机分布在20 m×20 m区域内的50 个UUV 初始通信连通,蓝色箭头表示航向,箭头大小表示速度大小。图4 为集群运动轨迹,集群沿全局期望速度q0=[4,3]m/s聚集,没有发生任何碰撞和分裂。在图5 中,集群最终状态趋于一致。图6 表示集群个体间距离变化,最大间距11.5 m 且小于2 倍的通信距离2Ri=13 m,最小间距0.9 m 且大于避碰距离Di=0.3 m,与图5 结果一致,集群实现避碰且保持联通。在图7 中,UUV 速度从初始状态收敛与期望速度,其中x轴方向趋于4 m/s,y轴方向趋于3 m/s。图8 显示在t=20 s 后,集群平均位置误差收敛为零。综上,时延条件下UUV 密集集群聚集运动稳定且没有发生任何碰撞和分裂。
为了进一步验证方法的高效性,选取基于固定距离和固定数量的2 种方法[20]与文中方法进行对比分析,仿真环境与仿真参数相同。定义2 个集群运动特性指标分别为平均航向和尺度参数,其中平均航向定义为
式中,N表示集群规模,其值越大集群越混乱。
尺度参数定义为
从表1 中可以看出,3 种方法的2 种性能指标均可收敛,但是文中方法的收敛速度和性能更好。一方面,由于q0=[4,3]m/s,标准航向为36.8,文中方法在t=30 s 时已收敛至36.8,但其他方法需要在t=60 s 才能完成,且精度36.9 和37.1 均低于文中方法。另一方面,文中方法的集群尺度参数在t=20 s 时快速趋于0.32,而其他2 种方法尺度参数相对较大,集群聚集性较差。上述结果表明文中方法在集群聚集控制方面具有优越性。
6 结束语
针对时延条件下的UUV 密集集群聚集控制问题,受不同尺度生物仿生机理启发,设计仿生邻居筛选机制并建立集群结队交互模型,并基于一致性协议、引斥力势场函数和干扰观测器,提出一种密集集群自适应聚集控制方法。理论与实验结果表明,文中所提方法具有较好的控制精度和环境鲁棒性。下一步将在变时延条件下研究UUV密集集群的集群运动演化特性。
