发动机燃烧室中火焰对来流扰动的动态响应研究综述

杨立军，刘晓康，田 雨，姜霄震，李敬轩

(1. 北京航空航天大学宇航学院，北京 100191；2. 北京航空航天大学宁波创新研究院先进飞行器与空天动力创新研究中心，宁波 315800)

0 引 言

随着新一代空间站建造的深入,以及探月计划和火星探测计划的进一步开展,中国对大推力液体火箭发动机的需求不断增加。此外,随着国内外环保法规的日益严苛,贫燃燃烧、低NOx排放的航空发动机正在成为民用航空动力的主流,与之相对应的地面燃气轮机也同样朝着贫燃燃烧的方向发展。然而不管是大推力的火箭发动机还是贫燃燃烧的航空发动机、地面燃气轮机,都已经广泛观察到了热声不稳定现象[1-3]。

发生热声不稳定的本质是不稳定燃烧过程导致的热释放率脉动、火焰上游来流的速度扰动以及燃烧室声学系统中的声波振荡之间的非线性耦合[4-6]。根据Rayleigh准则,当燃烧室内的压力脉动和热释放率脉动之间的相位小于90°时,火焰会给整个燃烧室声学系统提供能量,这是发生热声不稳定的驱动源。但受黏性、热传导以及声辐射的影响,整个声学系统的能量会因此衰减。当驱动系统振荡的能量大于系统耗散的能量时,热声不稳定便会产生。这会导致燃烧装置的性能下降,严重时会使其损坏并失效。总而言之,热声不稳定具有形成机理复杂且危害大等特征。

确定火焰热释放率对流动扰动的脉动响应是理解和预测热声不稳定现象的关键环节之一。火焰受到来流速度扰动的影响,会以热释放率脉动的响应形式呈现。根据扰动幅值的大小可将火焰对其响应分为两种不同情况,线性响应和非线性响应。当来流扰动的幅值较小时,可以认为火焰对输入信号的响应是线性的,此时火焰的响应只与施加扰动的频率相关,这种线性响应规律可以使用火焰传递函数(FTF)来量化[7],并以无量纲热释放率脉动和无量纲速度扰动的比值来定义FTF。当来流速度扰动的幅值足够大时,其幅值对火焰响应的影响无法忽略,这个过程需要使用火焰描述函数(FDF)来确定,此时火焰通常会呈现出非线性饱和效应[8],即随着来流扰动幅值的增强,火焰响应会趋于饱和。

1 FTF/FDF研究进展

目前对FTF/FDF的研究主要从三个方面展开,分别是实验测量、数值仿真以及解析推导。

1.1 问题提出

对于火焰传递函数的实验测量,一般将火焰视为一个整体,通过上游给定调制的速度扰动信号,使用化学发光[9-13],激光干涉[14]或超声波飞行时间差[15]等方法来实现对火焰热释放率脉动的精确动态测量。以化学发光法为例,一般使用配备CH*或OH*自由基滤光片的光电倍增管或高速相机对火焰的动态发光强度进行获取,并根据层流预混或弱湍流预混火焰的发光强度波动和热释放率脉动之间的线性定量关系获得FTF/FDF。速度扰动则使用激光多普勒测速法、粒子图像测速法以及多麦克风法等方法获得。给定FTF/FDF计算公式如下:

(1)

在早期研究中,Ducruix等[11]对层流预混锥形火焰的FTF进行了实验测量,结果表明,火焰锋面的脉动幅值明显依赖于上游施加的扰动频率,且火焰对来流扰动频率的响应呈现低通滤波特性且存在截止频率。Noiray等[10]基于一个在火焰上游的可变长度共振腔试验系统对多孔板甲烷-空气预混小火焰进行FDF测量,结果如图1所示。分析测量结果可以发现随着来流扰动幅值的增加,FDF的幅值会下降,火焰对扰动的响应呈现非线性饱和效应,但是FDF相位变化并不明显。

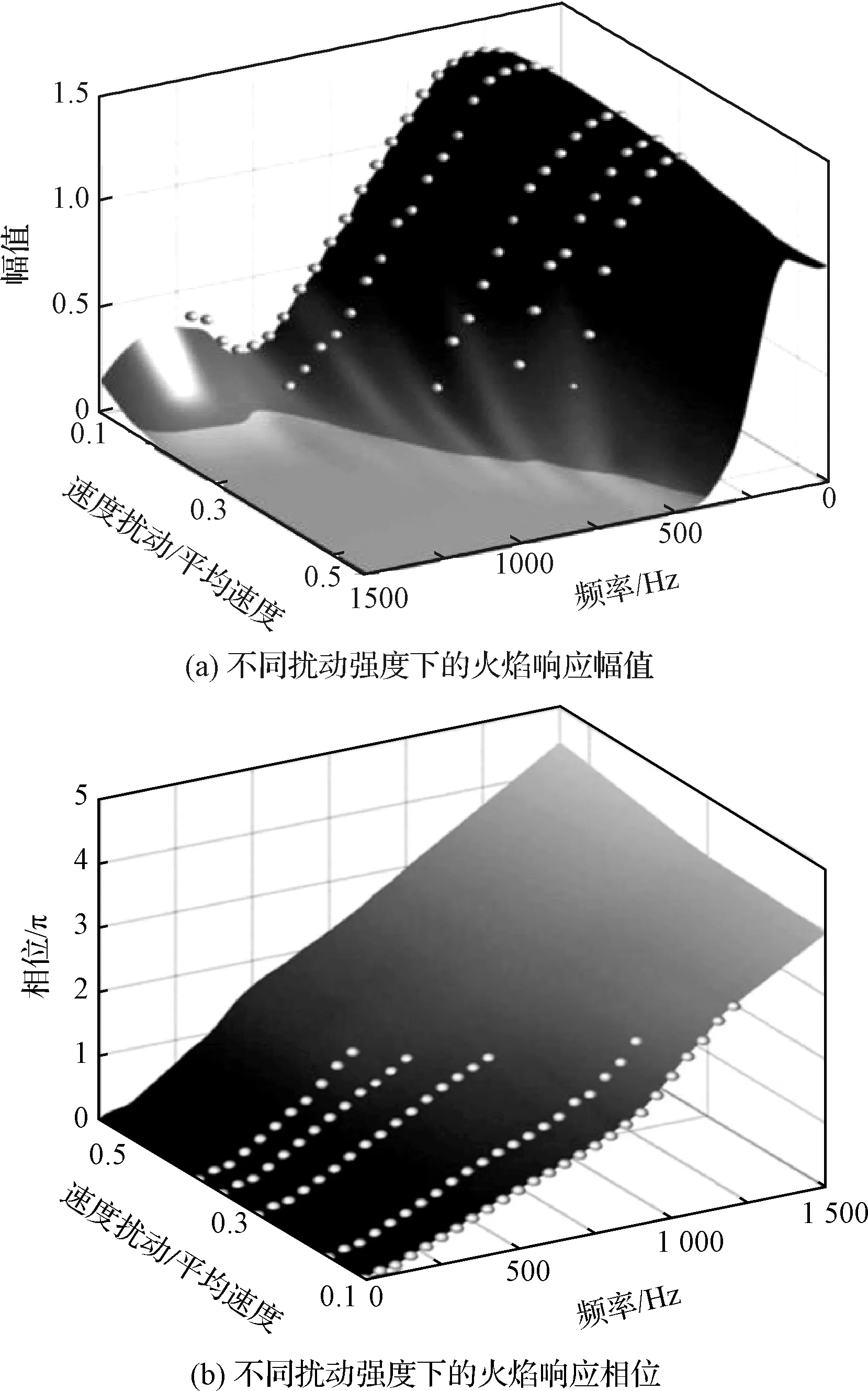
图1 FDF实验结果[10]Fig.1 FDF experimental results[10]

Durox等[13]测量了锥形、V形、M形以及多锥形层流预混火焰的非线性响应特性,通过分析4种火焰类型的FDF测量结果发现不同火焰类型的FDF差异较大。具体而言,在低频段,单锥形火焰FDF的幅值受来流扰动幅值的影响较弱,且相位随着频率线性变化;但在高频下相位随着频率的增加会出现饱和;其次,V形和M形火焰FDF的幅值在中频下会超过1,此时FDF幅值随着来流扰动幅值的增加而下降,而相位受来流扰动幅值的影响不明显,且随着频率的改变会呈现出准线性特性;最后,多锥形火焰的FDF幅值在较窄频段内超过1,且其受来流扰动幅值影响而减小的特性随着频率的提高而变得明显;FDF相位的斜率会随来流扰动幅值的增加而轻微变大,但其在频率变化过程中仍然呈现出准线性的特征。总而言之,火焰结构等特性会强烈影响火焰的非线性响应特性。

FTF/FDF测量关键是热释放率的测量,然而传统的基于化学发光法的测量方法通常局限于层流预混火焰。Li等[14-15]创新地提出了两种实验测量FTF的方法。首先,克服了光学测量方法直接测量热释放率的限制,发展了一种新型的超声波测量火焰热释放率的方法[15],通过测量超声波在所测区域内飞行时间变化来捕捉火焰前锋面的运动轨迹,最终量化火焰热释放率脉动以计算FTF,结果表明该方法具有较强的创新性和适用性。其次,基于燃烧热释放率变化与密度变化的关系发展了使用激光干涉法测量密度变化进而量化火焰热释放率脉动的方法[14]。这种方法可以摆脱传统化学发光法只能测量层流预混或弱湍流预混火焰的局限性,此方法的成功实验意味着湍流扩散火焰热释放率脉动的测量成为可能。

最近,Wang等[9]针对具有上游声学扰动的旋流预混稳定火焰的FTF幅值和相位分别进行了测量,发现了幅值随着驱动频率的变化和相位对频率的导数随频率的变化高度一致,幅值和相位导数在关于频率的函数中本质上是线性关系,这就意味着FTF的幅值和相位并不是相互独立的。针对这一现象,他们发现可以使用解析分解的方法对其进行解释。周期振荡旋流火焰的FTF可以认为是所有扰动机制的复杂矢量,通过矢量分解将FTF结果分解为二矢量模型,进而很好地解释了幅值和相位导数的同步变化特性。

1.2 仿真研究

为进一步理解FTF/FDF内在机制以及探究在复杂情况下火焰对上游扰动的响应机理,科研人员通过仿真方法进行了深入研究。

为了更深入地认识旋流湍流预混火焰的非线性响应饱和现象,Krediet等[16]基于大气环境下旋流稳定的湍流预混火焰的实验结果进行了大涡模拟,探究其响应的饱和机制并与已有文献的实验结果[17]相比较。他们通过在燃烧室进口边界条件处施加单频率的谐波,通过改变施加谐波的幅值和频率来获得FDF,得到的结果和文献实验结果[17]吻合较好。此外他们对旋流预混火焰的研究结果表明,火焰锋面面积随着来流扰动幅值增加而出现的非线性演化现象是导致火焰出现非线性响应特性的主要原因。对结果进一步分析发现,在引起火焰非线性响应的上游速度扰动中,主要是轴向方向上的速度扰动起作用,而与周向速度扰动的关系不大。

Han等[8]针对钝体稳定湍流预混火焰使用结合火焰面密度和分型方法来模拟湍流中的褶皱因素,并据此发展了一种开源大涡模拟方法来探究湍流预混火焰受上游速度扰动下的非线性响应特性。为了验证数值仿真结果的可信性,将获得的结果与文献实验结果[18]比较,两者吻合得较好。同时发现,改变火焰上游共振腔的长度对FDF的影响极小,这为未来长火焰燃烧室的稳定性和极限环的分析提供了新的视角。

1.3 理论研究

实验方法和数值模拟方法对FTF/FDF的特征有深入且全面的认识,且获得的结果也翔实可靠。但必须指出的是,实验和数值模拟方法仍然存在一定的局限性。相比于解析推导方法,其经济和时间成本无法忽略。因此,对现有FTF/FDF问题进行适当简化,使用解析推导的方法捕捉火焰对于上游输入扰动响应的基本特征具有较广的适用范围。

目前通用的描述火焰响应的方法为基于火焰面来描述燃烧热释放率,又称为解析推导方法,其本质是使用G方程捕捉火焰前锋面的动态演化。

(2)

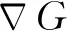
(3)

式中:YF为燃料的质量分数;A为火焰面积;ρ为火焰上游工质的密度。针对层流或弱湍流预混火焰,存在以下近似关系:

(4)

因此,可以通过无量纲火焰面积波动获得无量纲热释放率脉动:

(5)

进而可以计算FTF和FDF。

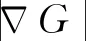
Lieuwen[21]使用G方程捕捉受到来流扰动且以一定火焰传播速度传播的层流预混火焰前锋面,并详细探讨了火焰的非线性响应规律。结果表明,解析结果得到的火焰非线性响应特性与实验结果[22]吻合较好。由于非线性现象存在,随着上游来流扰动幅值的增加,FDF的幅值低于FTF的幅值的特性明显加强,而FDF的相位对来流扰动幅值的变化并不敏感。火焰响应的非线性效应和Strouhal数St(St等于上游扰动频率和管出口直径的乘积并除以层流火焰燃烧速度)、稳态火焰高度、宽度比值β,以及火焰的类型(锥形火焰和V形火焰)密切相关。在火焰线性响应的特殊情形下,可以将St和β这两个参数整合为参数St2=St(1+β2)/β2。此外,同样发现,V形火焰的非线性响应特性比锥形火焰更明显。

在G方程中考虑湍流的思路有两种。第一种是在式(2)中的火焰传播速度项S里考虑湍流,即认为火焰以湍流燃烧速度ST向前推进,这种方法由Lipatnikov等[23]首次提出,被称为无强迫火焰模型(UFSM)。值得注意的是,在利用这种方法构建湍流预混火焰响应模型之前,需要通过其他方法来量化ST。Lipatnikov等[24]量化了湍流传播速度,表达式如下:

(6)

式中:S0为完全发展的湍流传播速度;t为湍流长度尺度;u′为湍流速度尺度;t′为火焰发展时间。将式(6)代入到式(2)中即可量化湍流火焰受上游声波扰动的动态响应特性。但需要指出的是,在这项研究工作中忽略了火焰垂直于自身向前发展而引入的非线性源项因此其得到的FTF幅值在低扰动频率下不够准确。

Palies等[25]使用类似的方法计算了旋流湍流预混火焰的传播速度并在此基础上结合G方程推导了FDF。他们首先给出了火焰的传播速度:

(7)

(8)

式中:i表示虚数单位;相位差φ通过实验[12]获得。

第二种考虑湍流的思路是在式(2)的火焰上游速度描述项u里引入湍流波动,这种方法最开始由Preetham等[26]使用,他们在火焰上游中考虑湍流波动并使用水平集方法来获取锥形湍流预混火焰受上游来流扰动的响应规律。Hemchandra等[27]借鉴这种方法构建了V形湍流预混火焰受上游来流扰动的非线性解析模型。他们使用高斯密度分布函数来量化湍流波动,并根据泰勒假设将湍流波动整合到上游速度中,以此来量化受湍流影响的V形火焰动态特性。

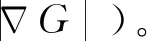
使用简化模型来量化上述扰动传播速度和扰动频率的关系并将其耦合进G方程的模型中十分必要,火焰褶皱会通过对流特性反馈影响火焰周围的速度场。Birbaud等[29]基于该思路,提出了基于火焰上游速度势的模型来定量分析火焰上游扰动传播速度和频率之间的关系,其结果所呈现出的空间特性与实验吻合较好。

通过对现有使用解析推导得到的FTF/FDF结果的回顾可以发现,FTF/FDF的解析方法在捕捉层流预混火焰的动态响应规律、非线性响应特性以及湍流预混火焰基本响应特性方面都具有一定的可行性。但目前大部分FTF/FDF的解析推导工作仍然局限于模型简单的单一输入。对于火箭发动机、航空发动机和燃气轮机中被广泛观察到的多模态耦合影响下的火焰动态响应特性、火焰拉伸对真实发动机中的火焰模型的影响的研究尚少。因此,借鉴现有FTF/FDF解析推导方法的思想,并将其推广并应用至多模态、考虑曲率影响下火焰响应性规律的研究中具有重要意义。

2 横向和纵向扰动下火焰响应特性研究

在火箭发动机以及航空发动机、地面燃气轮机的环形燃烧室中广泛观察到横向流动扰动和纵向流动扰动同时存在的现象。已有研究表明,火焰上游横向扰动的存在会显著影响火焰对来流扰动响应的整体特性。下文主要讨论使用解析方法来量化横纵向扰动耦合下的火焰动态响应特性。

Palies等[25]构建了受来流扰动影响下的旋流预混湍流火焰线性响应解析模型,并将时均的湍流波动使用UFSM的方法代入线性化的G方程中来捕捉湍流火焰的褶皱前锋面。此模型首次同时考虑了轴向和横向扰动对旋流火焰动态响应特性的影响。结果表明,旋流火焰的动态响应特性可以参考受轴向扰动下锥形预混火焰的FTF进行分析。将两种工况下得到的解析结果和实验结果[12]分别进行比较,结果定量吻合较好。这意味着,使用解析推导方法量化存在多向扰动影响下的湍流预混火焰动态响应特性是可行的。

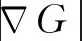
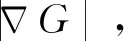
进一步,针对具有横向和纵向速度扰动和平均流的二维槽道层流预混火焰建立了完全/部分非线性FDF和线性FTF,明确了单向扰动自非线性和双向扰动耦合的互非线性对火焰热释放率响应的影响[34]。基于G方程结合渐进分析方法得到了火焰前锋面轨迹。提出了一种基于K(表征纵向平均速度和扰动传播速度的比值)和无量纲角频率St(角频率与燃烧器半径的乘积除以纵向平均速度)的分析模型,量化了特定频率St对应的扰动传播速度。如图2所示,得到了不同双向扰动幅值下的线性和完全/部分非线性热释放率脉动响应的整体差异。

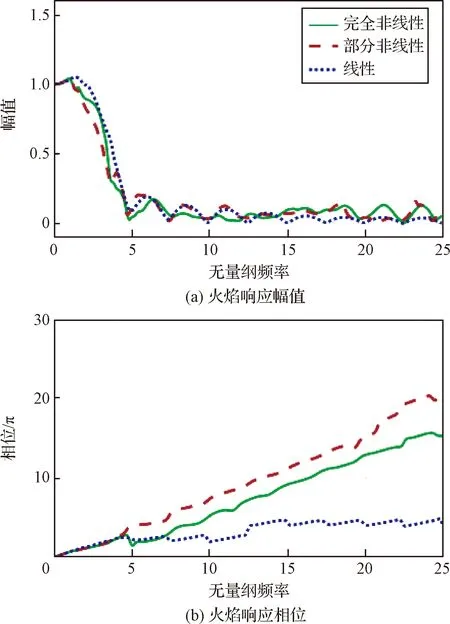
图2 双向扰动输入下火焰的线性、部分非线性和完全非线性响应结果随无量纲频率的变化关系[34]Fig.2 The linear, partially nonlinear and fully nonlinear response results of the flame under bidirectional perturbation input as a function of non-dimensional frequency[34]

研究结果表明,当纵向扰动幅值变大时,火焰响应的非线性特征十分明显,此时线性和非线性响应的幅值差异明显(部分非线性和完全非线性的结果差异同样明显)。通过对比FDF和FTF的相位可以发现,横向扰动对相位的影响不明显,特别是此时部分非线性结果和线性结果的相位几乎没有差别。而纵向扰动幅值的增加会在自非线性项中抑制扰动的传播(和线性结果相比,相位差增加),但在互非线性项中增强扰动的传播(和部分非线性结果相比,相位差降低)。总之,当扰动频率较高或扰动幅值较大时,自非线性项和互非线性项在火焰对双向扰动响应中无法忽略。

为修正火焰以恒定传播速度垂直于火焰锋面向反应物发展这一假设产生的误差,课题组期望改进经典的UFSM方法,以克服其对G方程进行一阶线性化忽略火焰垂直于自身向前发展的非线性源项而引入的缺陷,量化了二维槽道非对称预混火焰前沿动态对特定双向扰动的非线性响应,将该方法命名为双向非线性无强迫火焰速度模型(2W-NUFSM)[35]。具体而言,此方法基于无量纲横向扰动幅值和纵向扰动幅值的两参数二阶摄动方法描述火焰前沿动态轨迹,并将湍流效应通过火焰前沿推进速度和稳态火焰锋面两个参数考虑至模型中。为了使用2W-NUFSM量化谐波扰动耦合湍流波动对火焰前沿动态的影响,需要提前确定火焰前沿传播速度和稳态火焰锋面对湍流波动的响应特性。此外,改进了Hemchandra等[27]的方法,基于湍流波动幅值将火焰前沿方程渐进展开至二阶精度,并求解了湍流波动下的火焰传播速度和集总平均火焰锋面,分析了湍流波动对FDF影响的途径并进一步确定了谐波扰动和湍流波动耦合作用对火焰响应的影响规律。

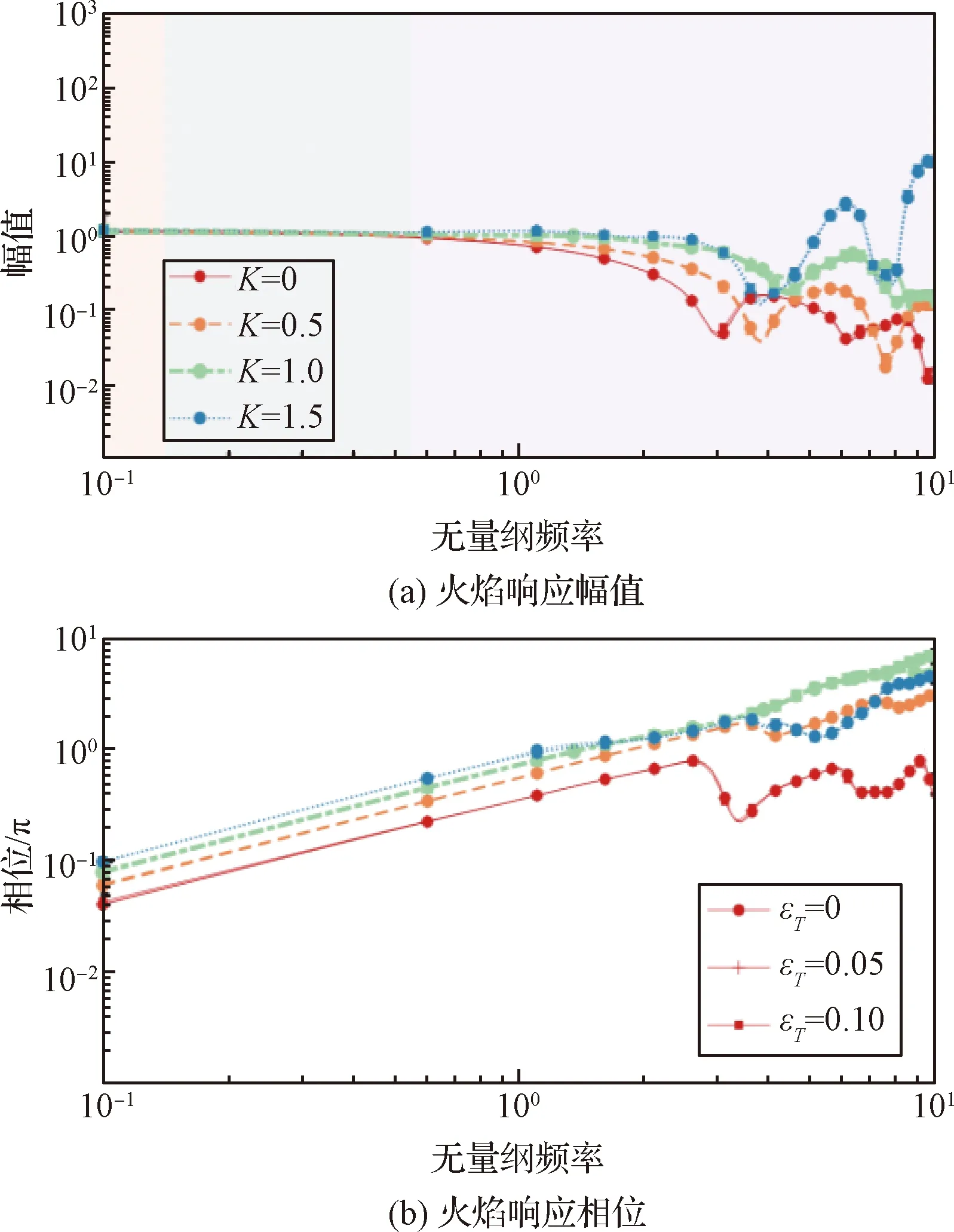
图3 火焰响应幅值和相位随着无量纲频率以及不同K和εT变化而变化[35]Fig.3 The flame response amplitude and phase vary with non-dimensional frequency as well as with different K and εT variations[35]

当谐波扰动频率较低时,湍流直接通过湍流波动幅值εT影响FDF的幅值。当谐波扰动频率在中频或者高频时,湍流通过K(与扰动传播速度uc负相关)影响FDF幅值。当谐波扰动频率较低时,湍流对FDF相位的影响主要由K控制,但当扰动频率较大时,上述关系将被扰动频率St影响。由于存在火焰运动学恢复效应,尺度越小的褶皱(对应于越小的uc即越大的K)越容易被运动收缩抹平,进而导致火焰动态响应幅值消散。当扰动频率增加,谐波扰动的波长减小。当谐波扰动波长与湍流褶皱的尺度相同时,火焰运动学由谐波扰动和湍流波动同时控制。由于小尺度褶皱诱发产生大幅值褶皱,因此火焰运动学收缩对火焰前沿褶皱的消除随着K的增加而增加,与K对FDF幅值复杂的影响不同,其对相位的影响更有规律且较轻微。

3 纵向双(多)频率扰动下火焰响应特性研究

多模态扰动耦合振荡影响火焰的现象广泛存在于发动机的燃烧室中,火焰与声波的耦合会激发出多种频率下的响应。多频扰动并非简单的单频线形叠加,而是具有新模态生成、模态抑制、模态强化等非线性作用。因此目前广泛研究的单一频率下的扰动有很大的局限性,双频扰动的研究更加贴合发动机的实际工作环境。

Balachandran等[36]对V形层流预混火焰输入两个不同频率的谐波扰动,来探究火焰的非线性响应特征。结果显示:由于额外引入的谐波或者亚谐波扰动,涡的形成和脱落过程明显受到影响。随着高频分量(320 Hz)的幅值增加,在160 Hz处的火焰传递函数收缩明显。此结果表明,可以通过对火焰引入特定频率处的额外扰动来抑制潜在的热声不稳定性。Lamraoui等[37]实验研究了具有两个非谐波相关不稳定模态(180 Hz和280 Hz)的湍流旋流预混燃烧室的热声不稳定性。与先前典型的单不稳定模态主导的现象相比,额外不稳定模态的引入不仅深刻改变了火焰的动态响应特性,同时也影响了对应的热声不稳定性,其中低频模态影响了纵向的振荡,而高频模态导致了径向的流动褶皱。

Haeringer等[38]分析了高次谐波对FDF的影响,引入了新的FDF来量化高阶谐波对应的热释放率与相对应频率的速度扰动的比值,以此来扩充原有的FDF,并将其称之为扩展火焰描述函数(extend-FDF);详细介绍了如何确定extend-FDF,并将其用来预测极限环振荡。结果表明,extend-FDF获得的结果和全可压缩数值仿真模型的结果吻合的较好。这意味着当高次谐波对热声极限环振荡起决定性作用时可以使用extend-FDF来描述实际火焰响应。

Orchini等[39]将FDF耦合到燃烧室的线性声学网络中,通过谐波平衡方法来预测谐波热声耦合振荡的幅值和稳定性。然而在某些特定工况下燃烧室内会出现多个非相关的频率进而产生非周期振荡。他们对这一现象进行简化,认为只有两个基础频率影响火焰响应,此时整个声学系统以准周期的形式发生振荡。以此将FDF推广来确定火焰对同时存在两个频率不同,幅值不同和相位不同的来流扰动的动态响应特性,并将其称为双输入火焰描述函数(FDIDF)。使用G方程针对层流预混锥形火焰构建了非静态DFIDF,并将其与热声网络进行耦合,以此来预测谐波热声耦合振荡的幅值和稳定性。通过与经典FDF比较,发现DFIDF具有预测Neimark-Sacke分叉和非稳态极限环状态下系统的振荡频率的能力。因此,在存在多频扰动耦合振荡的燃烧室中,考虑多频扰动耦合对火焰动态响应的影响是关键且必须的。

本课题组为了明确额外扰动对火焰受原有扰动影响的响应特性的改变,给定了两个频率、幅值、相位都相互独立的谐波扰动(分别命名为原有扰动和额外扰动),并将其输入火焰来探究它们在火焰响应中的非线性耦合机制。火焰响应的非线性结果通过G方程结合低阶渐进分析(扩展至关于无量纲扰动幅值的三阶)和数值方法获得。由于火焰垂直于自身向反应物一侧发展,基于渐进分析可知,原始扰动和额外扰动在火焰响应中产生了三阶非线性耦合并改变了火焰在原始扰动频率处响应。其典型结果如图4所示,可以发现,火焰在原始扰动频率处的响应主要由线性项构成,而非线性项在此基础上对其幅值和相位进行修正。随着火焰向下游发展,火焰响应的幅值衰减明显,相位的阶跃现象也得到抑制。

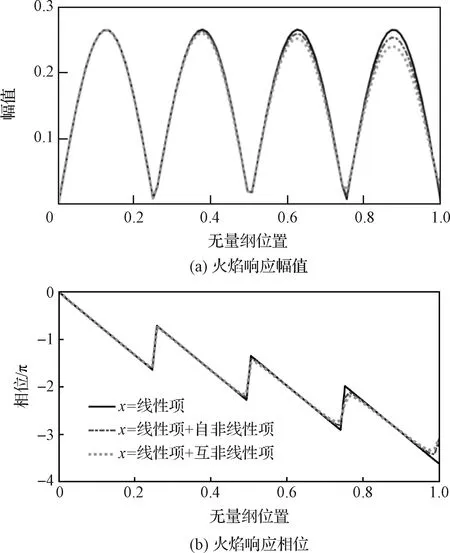
图4 原始扰动频率处火焰空间响应对原始和额外扰动非线性的依赖[40]Fig.4 Dependence of the spatial response of the flame at the original perturbation frequency on the original and additional perturbation nonlinearities[40]

4 火焰曲率效应对FTF/FDF的影响作用

当火焰尺寸较小时,由于张力和热扩散的影响,火焰传播速度受到流动梯度的影响,导致每个位置的火焰拉伸不同,进而影响了整体放热速率。因此,锥形火焰锋面在一定频率范围内会变成半球形,这进一步凸显了考虑火焰曲率效应的必要性。

在G方程模型中,火焰曲率拉伸速率对火焰速度的影响通常由马克斯坦长度L表示,一般结合火焰厚度将其表示成无量纲形式——马克斯坦数L/δ,此参数主要反映不同的燃料种类及当量比。常用的几种碳氢氧燃料的对应关系已通过实验进行研究[41],其中氢气和甲烷的马克斯坦数随着当量比增大而增大,而其它绝大多数燃料,两者呈负相关。

火焰曲率拉伸通过影响火焰燃烧速度,进而影响火焰热释放率,因此在理论上对G方程中的火焰传播速度SL进行修正[42]:

(9)

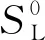
Preetham等[43]的研究结果表明,火焰曲率拉伸会影响燃烧速度沿火焰褶皱锋面的传播情况,整体线性火焰响应取决于马克斯坦长度和无量纲Strouhal数。当LSt～O(1)时,火焰曲率拉伸效应会变得明显,并导致火焰锋面褶皱减小,此现象表明组成LSt的马克斯坦长度、火焰高径比、平均流速和特定频率是决定火焰曲率拉伸效应是否显著的关键参数。Wang等[44]进一步的理论研究表明,当扰动频率在一定范围时,火焰曲率拉伸效应在火焰传递函数中发挥着重要作用。具体来说,低于某一扰动频率时,火焰曲率拉伸效应很小,火焰响应与未考虑拉伸时基本一致;而高于此频率且在一定范围时,火焰面积受火焰曲率拉伸的影响强烈,进而影响火焰传递函数。

从实验结果来看,火焰曲率拉伸的作用同样非常明显,其中小尺寸火焰受影响较大。Kornilov等[45]的研究结果表明,多孔火焰的孔径和孔隙率是影响火焰传递函数和火焰描述函数的主要参数,主要影响在于会使幅值在特定频率范围内超过1。此外,当孔隙率不变时,随着孔径减小,火焰传递函数幅值随频率先增大而后降低的过程变得缓慢,相位降低;当孔径不变时,孔隙率越大,相位越大。上述现象可通过不同尺寸火焰的形状受到拉伸的影响程度不同来解释,此研究为多孔火焰燃烧器喷嘴的设计提供了参考。

Gaudron等[46]引入了无量纲频率,将不同尺寸的火焰进行相似性类比。当火焰尺寸较大时,相似尺寸火焰的传递函数表现出相似性,无量纲处理后基本重合;而当火焰较小时,由于火焰厚度相比火焰半径来说不可忽略,需要额外的参数来完整描述FTF。此外,结果表明,特定的路易斯数和火焰温度会导致小火焰传递函数在低频时增益值超过1,称为增益过冲。由图5可知,在低频速度扰动下,当喷嘴尺寸减小或火焰温度降低时,传递函数峰值对应的无量纲频率较低。基于此实验结果完善了考虑火焰底部相邻火焰相互作用和不稳定传热传质的模型,相较于基于平面火焰的模型,此模型更准确。

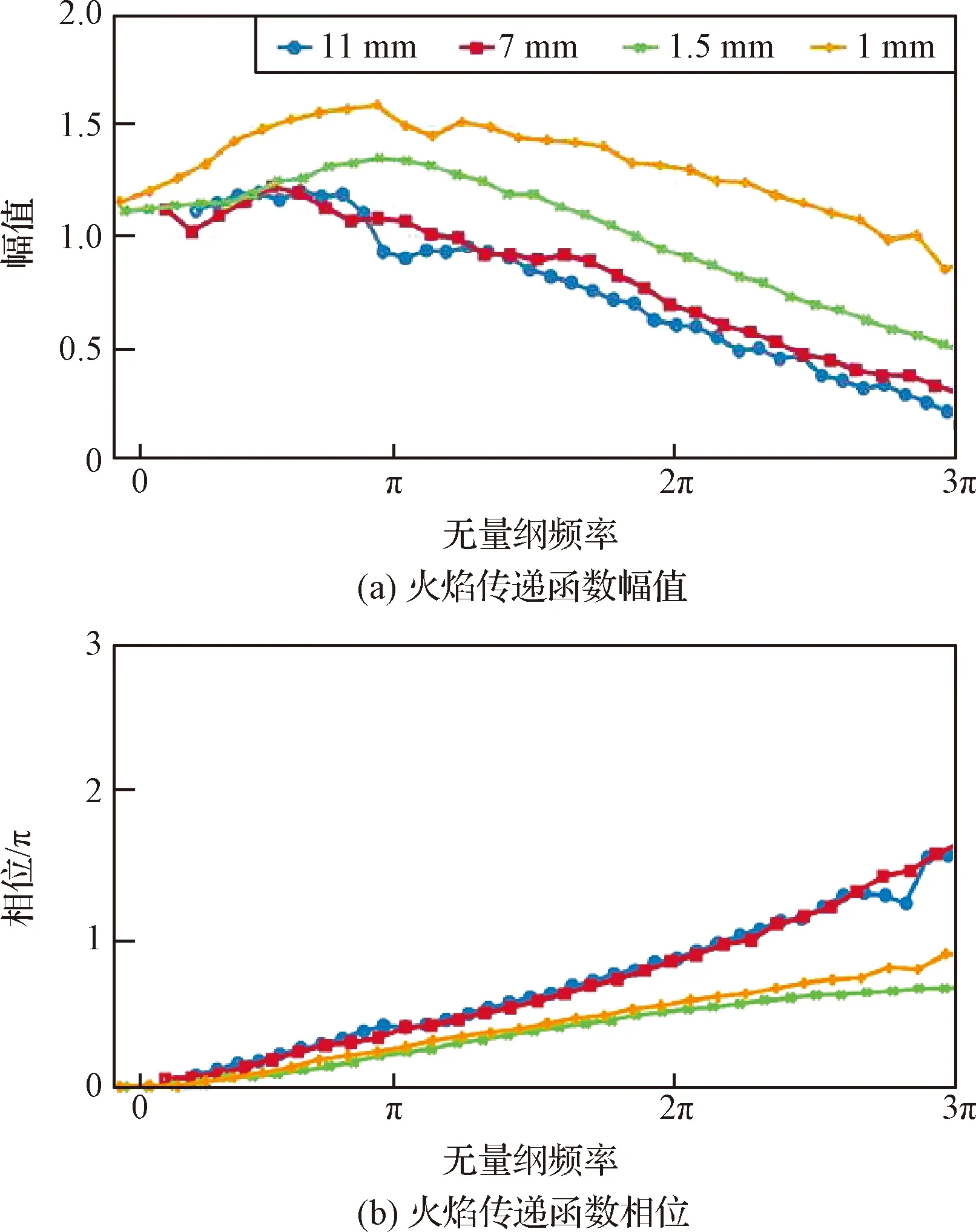
图5 不同喷嘴半径的火焰传递函数[46]Fig.5 Flame transfer function for different nozzle radius[46]

Kedia等[47]通过数值仿真方法研究了火焰根部的锚定情况对火焰曲率拉伸的影响。结果表明,火焰根部会锚定在流动速度和火焰位移速度相同的地点,该位置由热损失和火焰拉伸对火焰位移速度的综合影响决定。随着反应物入口速度的增加,该位置的火焰位移速度呈非单调变化,变化主要表现为:回流区逐渐扩大,火焰向下游移动,燃烧器的热损失减少,火焰加长,位移速度增加。而入口速度的进一步提高会导致吹熄,吹熄期间的火焰速度由增长的再循环区和冷却燃烧器板之间的反馈决定。

Cuquel等[48]对火焰根部和燃烧器喷嘴之间的不稳定传热响应进行了理论研究,并称之为火焰基振荡,修正了锚点运动时的火焰传递函数,并将修正前后的结果进行了比较。结果表明,传递函数相位出现非线性行为,速度扰动导致相位滞后随频率增加,而火焰基振荡导致相位滞后在高频下饱和,两者之间存在竞争。此外,扰动幅值的增加会导致火焰传递函数在较低频率下的相位滞后,提前饱和。该分析证明了火焰根部振荡在控制传递函数相位滞后饱和度方面的重要作用。

5 火焰传递函数对固有热声不稳定模态的影响

在热声不稳定的研究中,FTF/FDF的主要应用方式为代入到诸如线性欧拉方程、亥姆霍兹方程和低阶声学网络模型等求解器的热源项中来对流动扰动和热释放率扰动之间的相互作用进行说明,进而实现对热声不稳定性的预测。近些年来有学者将系统热声振荡模态基于燃烧室声学特征和燃烧特性进行了划分[49]。研究表明,即使在无声学反射的边界条件下,依然存在热声振荡现象,并将这种热声振荡现象命名为固有热声不稳定性(ITA)。

在早期研究中已经发现了在热声系统中存在很多难以解释的振荡模态,Dowling等[50]通过构建薄环形LPP燃烧器热声系统振荡的线性模型,结合简单的火焰模型对燃烧器内的热声振荡模态进行了预测,发现了许多无法解释的与声学特征值无关的热声振荡模态。但是这些问题通常被归结于火焰模型过于简单和线性模型不够完善,并未引起注意。在近些年的研究中发现,上述问题可以通过ITA模态进行解释,即实验中所测试到的热声振荡模态存在着两种主导因素[49]:一种是燃烧室声学特征主导的模态,被称为声学主导模态;另一种是由火焰响应主导的模态,这类模态被称为ITA主导模态。研究表明,在逐步去除燃烧室火焰响应和声学特征(边界声学反射)时,热声模态会分别退化至两种基本模态:纯声学模态(不存在火焰响应时的热声振荡模态)和ITA模态(不存在边界声学反射的热声振荡模态)。在多数情况下,燃烧室中的热声模态受到上述两种模态共同影响,且由其中一种模态主导。

热声振荡系统中的ITA模态是与火焰响应紧密相关的一种模态。对于这种ITA模态与火焰响应之间的关系,目前学界的基本认识为,在火焰处由于火焰耦合作用构成了一个内在的反馈环。如图6所示,其基本的反馈过程为:火焰受到上游一点的速度扰动后产生热释放率波动,热释放率波动作为声源会产生声波,声波向上游和下游传播,其中向上游传播的声波会在燃烧室入口、钝体等燃烧室上游结构边缘处产生涡脱落并造成流动扰动,随后流动扰动进一步向下游传播引发热释放率扰动,构成反馈环[51]。从上述过程可以看出,ITA模态与火焰本身性质密切相关,且与燃烧室内的声学特征无关,而与热释放率对于速度扰动的响应(FTF/FDF)有着相当紧密的联系。

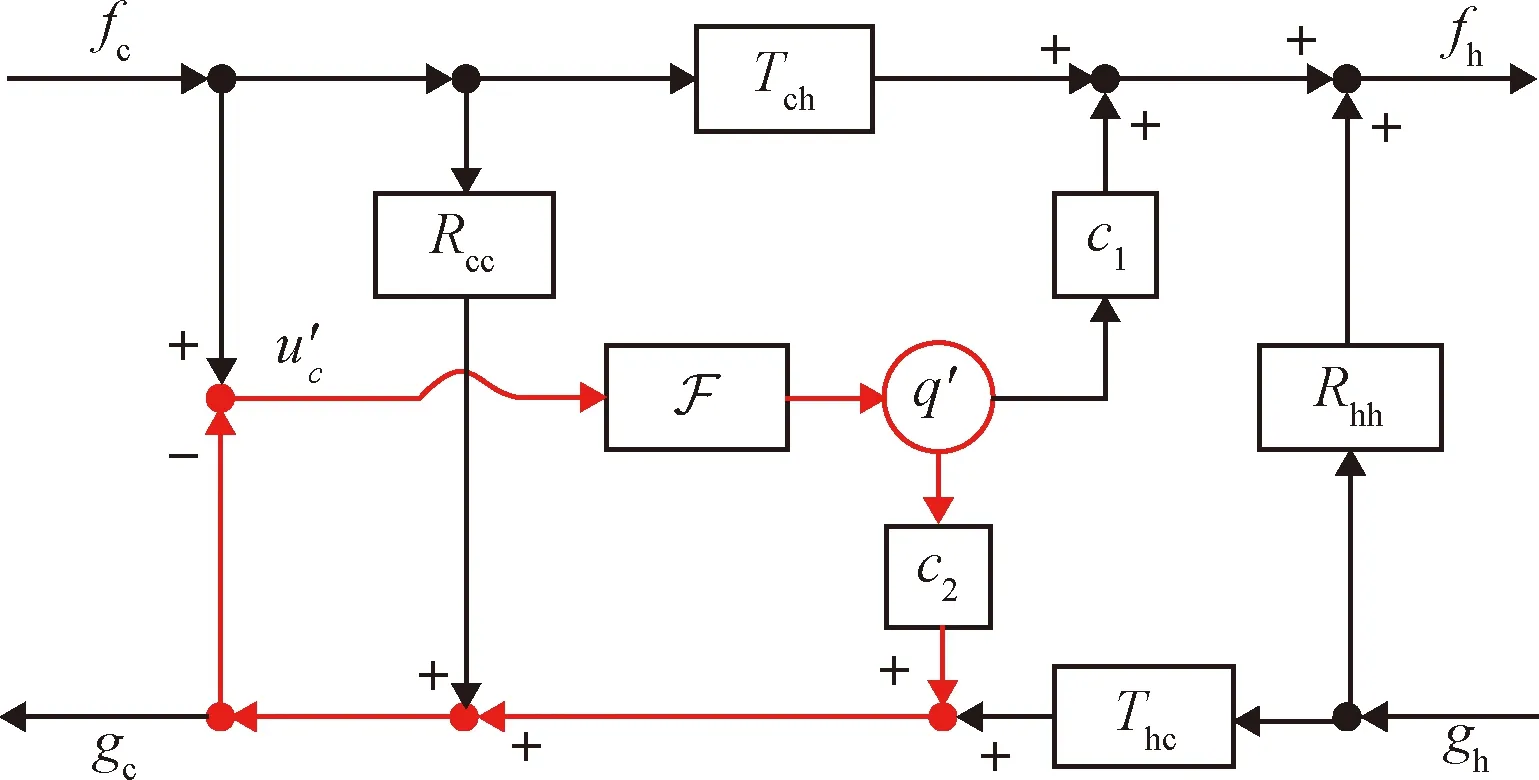
图6 ITA模态反馈环[52]Fig.6 ITA mode feedback loop[52]

在上文中,深入探讨了不同火焰对于不同方向、不同频率及不同幅值的速度扰动的影响作用。在下文中,将对火焰响应(FTF/FDF)和燃烧室中ITA模态之间的关系及进行讨论。讨论主要分为两个部分,第一部分为火焰传递函数和ITA模态之间相互作用的理论研究;第二部分主要讨论基于实验和仿真研究FTF/FDF与ITA模态之间的关系。

值得注意的是,下文主要是讨论FTF/FDF和ITA模态之间的关系,不同学者对于ITA模态的求解方式不同,目前主流的为:散射矩阵极点、低阶声学网络模型、开环传递函数、相量图、稳定性边界、亥姆霍兹方程和仿真求解等。以下讨论不会着重关注ITA模态的求解方式。

5.1 理论研究

在近年来对ITA模态的研究中,Hoeijmakers等[53]和Emmert等[54]的工作具有开创意义,通过结合n-τ构建低阶声学网络模型并对其进行简化,得到散射矩阵,随后通过散射矩阵对燃烧室的热声振荡进行讨论,发现了火焰内部存在ITA反馈环,进而提出ITA模态,其中n-τ模型如下所示:

F=ne-iωτ

(10)

式中:n为耦合强度;τ为相位延迟;ω=2πf+iσ,其中σ表示增长率,f表示频率。此外也通过散射矩阵的极点来说明了ITA模态的振荡频率及稳定性边界:振荡频率由n-τ模型中的相位延迟τ确定(又被称为-π准则,即ITA模态频率为1/τ);稳定性边界由燃烧室参数和n-τ模型中的耦合强度n确定。结果表明,随着边界反射系数的逐渐减小至0,燃烧室中的一些振荡模态逐步转向ITA模态。此外,通过仿真和实验方法验证了上述结果[55]。这一研究工作将燃烧室中的热声振荡模态进行了分类,并给出了完整的预测方法。

Hosseini等[56]和Sogaro等[57]通过将n-τ模型应用于一维Rijke管模型并通过低阶声学网络模型对其ITA模态进行预测,详细分析了燃烧室内各种参数如边界反射系数,耦合强度n、相位延迟τ和火焰处面积扩张比对ITA模态和纯声学模态之间的影响作用。结果表明,部分ITA模态和纯声学模态之间存在着周期性相互转换的关系。此外,通过伪光谱法分析发现,能量增大对纯声学模态和ITA模态之间的相互作用至关重要,而火焰是能量增大的主要来源。

Mensah等[58]、Buschmann等[59]、Silva等[60]、Orchini等[61]和Ghani等[62]在一维纵向和环形燃烧室中应用n-τ模型研究ITA模态时,发现随着火焰传递函数中n和τ改变,系统中的热声振荡模态分布出现明显的奇异点,且这一现象广泛存在。如图7所示,在奇异点附近,ITA模态具有非常大的灵敏度并表现出强烈的模态转向,此结果在三维轴向和环形燃烧室中进行了数值验证。上述研究中使用的研究方法为低阶声学网络模型或亥姆霍兹方程结合n-τ模型进行求解。上述结果说明燃烧室中的纯声学模态和ITA模态之间的相互作用受火焰响应影响极大,而对于真实的燃烧室系统的火焰响应,这种作用会更加复杂。

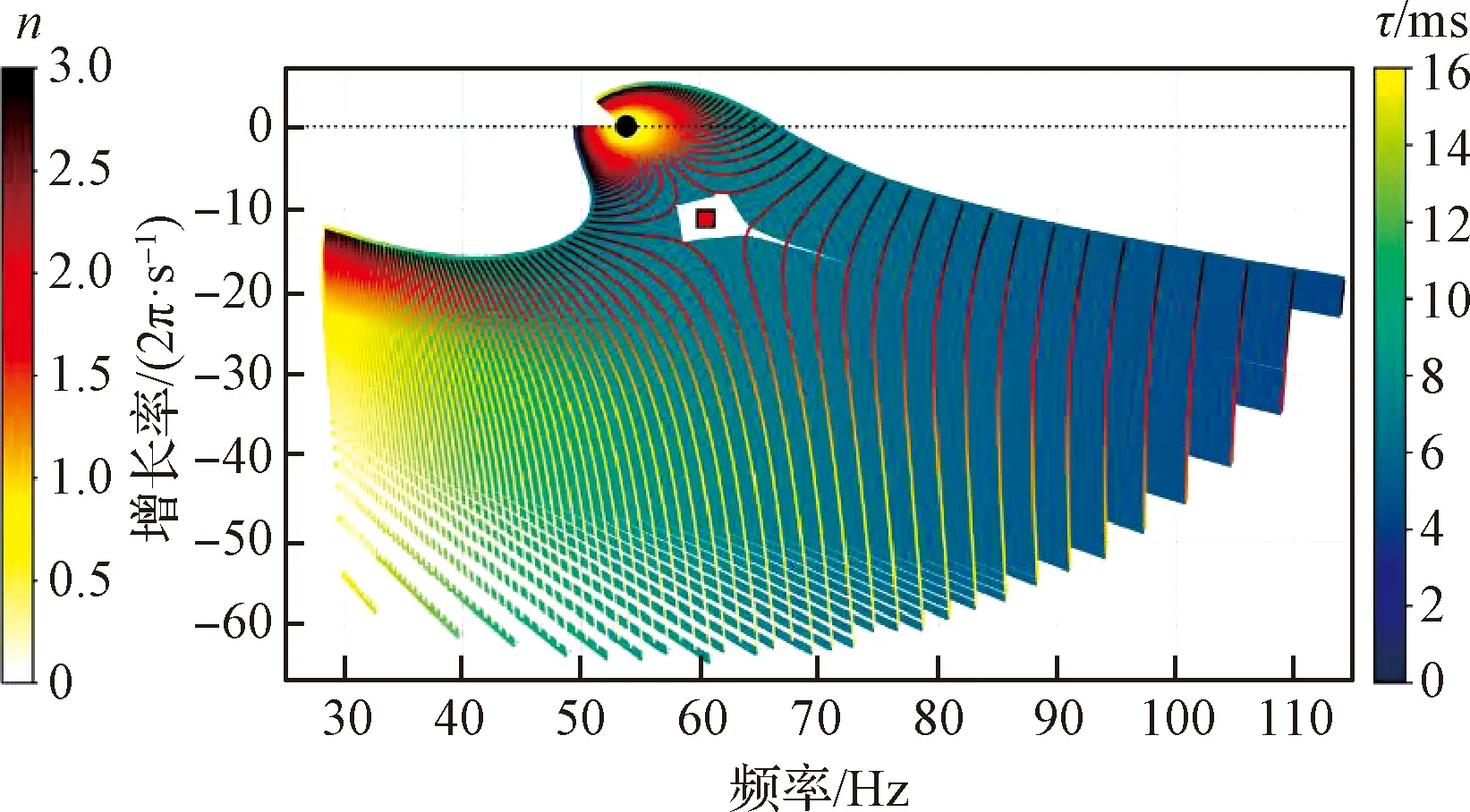
图7 特征值迹线中奇异点的位置(n和τ表示n-τ模型参数)[61]Fig.7 The location of exceptional points in the eigenvalue trajectories (n and τ represent n-τ model parameters respectively)[61]

Buschmann等[57]通过结合n-τ模型和亥姆霍兹方程的方法研究了薄壁环形燃烧室中的ITA模态并进行了仿真验证。结果表明,环形燃烧室中确实存在ITA模态,且ITA模态的分布也符合-π准则,此外模态分布具有成簇的特殊行为,即频率相近的几种模态,说明环形燃烧室中的ITA模态存在聚类现象。

本课题组也对一维Rijke管模型和环形燃烧室模型中的ITA模态进行了理论研究[63]。主要是通过应用n-τ模型,结合组内研究基础[64-65],并参考了Li等[66]的研究方法,构建了考虑平均流、涡波和熵波的更完善低阶声学网络模型并对ITA模态进行了研究。以往的研究忽略了平均流的影响作用[57],但是研究结果表明[63],平均流对ITA模态的增长率影响很大,而对ITA模态的频率影响不大,马赫数的增加使得所有ITA模式都更加不稳定,且对不同模态的稳定性影响不同。此外研究发现,当考虑平均流时,在环形燃烧室中发现了一种新的不符合-π准则的ITA模态,这一模态的存在很可能与环形燃烧室中的涡波和熵波有关。

5.2 实验和仿真研究

相较于简化的n-τ模型及基于其修正的火焰传递函数,基于仿真和实验数据提取的FTF/FDF更加完善且具有代表性。本节的主要研究思路为通过仿真和实验数据获取FTF/FDF,随后将其代入到低阶声学网络模型或者亥姆霍兹方程中进行ITA模态的求解,将求解得到的ITA模态与仿真或实验中观测到的热声振荡模态或ITA模态进行比对,从而进行分析。

早期对于ITA模态的仿真和实验工作主要是验证ITA模态的真实存在。Emmert等[54]和Bomberg等[67]通过系统识别的方法从BRS旋流燃烧器、ECP层流预混燃烧器、TD1湍流预混燃烧器实验数据和大涡模拟仿真数据中提取火焰传递函数。将火焰传递函数结果代入到由色散矩阵极点获得的开环传递函数中,并基于尼奎斯特判据对ITA模态的位置和稳定性进行预测,最后与实验和仿真观测结果进行对照。结果表明,理论预测结果和观测结果一致,说明ITA模态真实存在,且热声系统中的振荡可以由ITA模态引起。此外,Emmert等[54]还从声功率平衡的角度分析了火焰固有反馈回路与热声系统不稳定潜力的关系。

Courtine等[51]通过直接数值模拟的方法研究了预混本生灯火焰燃烧系统的ITA模态。通过对多种工况的对比分析,如图8所示,详细探究了ITA模态下一个振荡周期内的火焰面变化,基于火焰响应提出了ITA模态反馈环的理论解释,即模态转换和运动学过度恢复。值得注意的是,模态转换发生在燃烧室入口拐角处,受上游速度扰动的影响,此处会产生涡,而火焰的锚点也在此处,涡和锚点的相互作用引发了模态转换。在振荡周期的初始阶段,火焰锚点会被涡推开,火焰会被持续拉长,随后发生运动学过度恢复。由于此时火焰远离其平衡位置,且入口速度也是最小状态,所以火焰会快速收缩,而火焰的强烈收缩导致了负的扩张和声压,这反过来又诱发了火焰上游的速度激增。而入口速度的增加会再次诱发燃烧室入口拐角处的模态转换,并产生了一对新的涡,从而构成新的循环。可以看出,上述ITA模态的所有振荡过程和火焰响应,即FTF/FDF有着至关重要的直接联系,也正因此,对于火焰动力学的研究对ITA模态和热声振荡模态的研究具有重大意义。

ITA模态的实际实验测量需要消除声学的边界反射,Hoeijmakers等[68-69]提出了一种通过安装喇叭来消除边界声学反射的方法,并在边界存在大量声学损失的条件下对层流预混本生灯火焰的热声振荡进行了实验研究。此外,他们通过实验测量得到火焰传递函数,并将其代入低阶声学网络模型中进行ITA模态的预测。结果表明,即使在边界处存在大量声学损失的情况下,热声系统也会表现出不稳定性,这一实验结果证实了ITA模态的存在并为早期ITA模态的理论提供了实验依据。

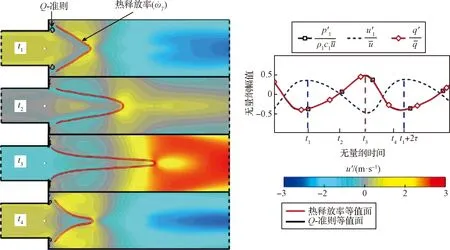
图8 固有热声不稳定振荡模态下的一个完整振荡周期(其中黑圈表示涡)[51]Fig.8 One complete period of oscillation in the intrinsic thermoacoustic instability oscillation mode, where the black circle indicates the vortex[51]

Silva等[70-71]和Albayrak等[52]对层流预混本生灯火焰和BRS旋流燃烧器分别进行直接数值模拟和实验研究。研究结果表明,对于上述的两种燃烧室,ITA模态均真实存在,且不受燃烧室声学特性的影响。值得注意的是,在对BRS旋流燃烧器进行的实验研究中,低阶声学网络结合系统识别得到的FTF预测的ITA模态结果与真实的实验结果一致性很好。从实验结果中还发现在这个特定的燃烧器中,ITA模态很普遍,并且不稳定的模态占比较多;ITA模态的频率随着体积流速和旋流器位置的变化而明显改变,但对燃烧室长度的变化不敏感。上述实验结果和规律对ITA模态和火焰响应直接的相互作用提供了坚实依据。

Murugesan等[72]和Vishwakarma等[73]对工业燃气轮机上实际应用的大雷诺数(Re>13000)湍流部分预混旋流燃烧器中的ITA模态进行了实验研究,其中燃料为体积占比40% C3H8和60% C4H10组合的液化石油气,空气由大型压缩机提供。结果表明,低阶声学网络预测的频率与实验观察到的振荡主频率非常一致。此外,非稳态热释放热率与燃料当量比波动之间的内在火焰声学耦合作用对ITA模态有极大的影响,而这种耦合作用需要通过火焰描述函数进行详细描述。

Ghani等[74]通过仿真方法研究了甲烷火焰中添加氢对ITA模态的影响作用。结果表明,氢燃料的加入增大了层流火焰速度,火焰整体长度明显缩短。通过系统辨识的方法对FTF进行提取,随着氢添加量的增多,火焰传递函数的幅值减小,相位增加。随后将提取的FTF应用于-π准则和稳定性边界来预测ITA模态,预测结果和燃烧室内真实压力振荡频率较为一致,且更大的氢的添加量增大了ITA模态频率,显著增强了同一频率下ITA模态的稳定性。上述结果说明可通过添加氢气来缩短火焰高度,改变火焰响应特性,进而实现ITA模态的控制。这一结果与Tang等[75]对“马克斯坦长度随着氢分数的增加而增加,表明氢的加入稳定了火焰”的论述一致,说明稳定的火焰有利于ITA模态的稳定。Cheng等[76]通过仿真方法探究了通过改变层流预混火焰中火焰稳定器的温度来改变火焰传递函数,从而影响燃烧器中的ITA模态。结果表明钝体温度通过改变火焰附着区域可以显著影响火焰响应,进而影响系统的ITA模态。上述结果证实了火焰响应主导了ITA模态,并对热声系统的振荡模态施加影响。

Xu等[77]基于预混旋流燃烧器研究了当量比和声衬对系统热声不稳定性的影响作用。实验和理论研究结果表明在更高的当量比下,ITA模态比声学模态更容易出现不稳定;此外,添加具有偏流的声衬可有效抑制腔内纯声学模态主导的燃烧振荡,但对ITA模态无效,且偏流马赫数的增加会激发和增强不稳定的ITA模态;当量比显著影响火焰传递函数,进而改变ITA模态。此外,结果中体现的声衬等常用的热声振荡抑制装置的加入对热声系统中ITA模态主导的振荡模态影响作用较为复杂,这也为热声不稳定的控制提供了一些指导和参考。

6 趋势与展望

基于上述分析,对火焰受来流扰动的动态响应发展趋势的概述如下:

1) 已有的理论研究主要集中于单模态扰动影响火焰的简单情形。然而,多模态扰动耦合振荡影响火焰现象广泛存在于火箭、航空发动机和燃气轮机的燃烧室中,如横纵向扰动耦合振荡以及单纵向多频率扰动耦合振荡等,其对应的燃烧不稳定也时有发生。现有文献中对于多模态扰动耦合作用下火焰动态响应特性的研究较少且没有对得到的结果进行详细的说明和进一步的机理解释。这显然限制了对多模态扰动作用下火焰动态响应规律的深入理解。因此,将多模态扰动耦合作用下的火焰模型进行适当化简,使用解析推导方法量化在它们的作用下火焰的动态响应特性,并深入探究其响应性规律,这对于理解和预测对应的燃烧不稳定具有重要意义。

2) 对火焰曲率的研究多局限于层流预混火焰受当量比影响而使得火焰形态发生变化,然而热声系统中流动扰动和热释放率扰动之间的耦合作用使得火焰曲率发生变化的机理非常复杂。火焰热释放率还会受到诸如壁面温度和重力场环境等多种因素的影响,各种因素的耦合作用的影响同样值得重视。此外,目前解析方法只能对较为简单的层流预混火焰进行解析求解,难以实现对上述多种因素影响下的各种火焰进行描述。这些问题均需要更完善的理论模型和实验研究,因此,实验技术和测量仪器性能的进一步提升对火焰动态响应的研究也有着至关重要的意义。

3) 为了实现对热声不稳定的控制,需要对热声系统振荡机理的深刻认识。对固有热声不稳定和火焰响应之间相互作用的机理研究对上述问题的解决起着决定性作用。但就目前的研究现状来说,理论研究的局限性一方面在于火焰响应模型过于简化,忽略了火焰的空间分布,以及缺少如旋流火焰、喷雾火焰和多火焰耦合的响应模型;另一方面在于固有热声不稳定的求解方法如低阶声学网络模型和线性欧拉方程等不够完善,难以实现对较复杂燃烧室内热声振荡模态的预测。此外,实验方面的局限性在于难以完全对常见的燃烧设备实现边界声学反射的消除,实验测量仪器的精度也难以满足燃烧室中的测量需求,也就难以实现对固有热声不稳定模态的精确测量,无法从实验的角度分析火焰响应和固有热声不稳定模态之间的相互作用。上述的问题也是目前的研究趋势和进一步的研究方向。

7 结束语

本文聚焦火箭发动机、航空发动机和燃气轮机的燃烧室内广泛观察到多模态耦合振荡产生热声不稳定,研究了火焰对多模态流动扰动的非线性响应特性,具体着眼于横纵向扰动耦合和纵向双频扰动耦合作用下的火焰动态响应;此外考虑了火焰曲率拉伸对火焰传递函数的影响作用;最后对近年来出现的一种在燃烧室内与火焰传递函数和火焰描述函数紧密相关的固有热声不稳定模态进行了讨论,着重分析了火焰响应对固有热声不稳定模态的影响作用。