“旋相为宫”的历史探索及律学分析

崔磊

中国较早记录乐律计算方法的史料文献包括《管子·地员篇》及《吕氏春秋·音律篇》，但二者著作年代孰早孰晚说法不一，由此“三分损益法”产生于何时，成为“一个有争议的问题。”[1]不过，通过推理，学界前辈认为《管子·地员篇》产生年代应早于《吕氏春秋》。尽管有着“当时著作多代表一家之言而非一人之作”的顾虑，考虑到《管子·地员篇》虽有详备的宫、徵、商、羽、角的生成记载，但也只算到五个音，“从历史发展的一般规律来看，它只算到五个音，比之算全十二个半音的《吕氏春秋》，应该更早一些。”[2《] 律学》一书支持该观点，同样有学者认为“‘三分损益法最早见于《管子·地员》，记录生五音的方法和顺序，后《吕氏春秋·季夏纪·音律》规定了生十二音的顺序。”[“3]‘京房六十律用的生律法是首见于《管子·地员》的三分损益法。”[4]此外又有研究者研究发现《管子》中只算到五个音是因其与琴相关，这五个音正合古琴“正调”[5]。

一、“三分损益”相生五音、十二律

《管子·地员篇》相关生律方法称为“三分损益法”，关于“三分损益法”是根据管的长度还是弦的长度进行计算，亦有不同看法，不过根据目前从音响、文献、现存乐器（包括琴、管）的相关研究来看，“三分损益法”更大可能为“三分损益弦律”，如文：

“凡将五音起，先主一而三之，四开以合九九；以是生黄钟小素之首，以成宫。”[6]

其中“黄钟小素”之“小素”即为弦。张尔田《清史稿·乐志二》中解释，

“小素云者，素，白练，乃熟丝，即小弦之谓。言此度之声立为宫位。其小于此弦之他弦，皆以是为主。”[7]

该方法具体是将振动弦长平均分成三段，采用益一（增加原弦长的三分之一）、损一（舍去原弦长的三分之一）的方法求得下一律。《管子·地员篇》相关记载具体为，“

凡将五音起，先主一而三之，四开以合九九；以是生黄钟小素之首，以成宫。三分而益之以一，为百有八，为徵。不无有三分而去其乘，适足以是生商。有三分而复于其所，以是生羽。有三分而去其乘，以是生角。”[8]

文献可知宫音弦益一得徵音，徵音弦损一得商，商音弦益一得羽，羽音弦損一得角，相关律数依次为81、108、72、96、64，按照从低到高的音高顺序排列应为：徵、羽、宫、商、角，实则得出徵调式音阶，此亦是上述所言古琴之“正调”。三分损益法所设定的律数皆为整数，其中“四开”的设定体现了古人的数理智慧，“先主一而三之”而后“四开”正可以使得相生五音之律数为整数，且“这种有理数的整数比关系是符合自然法则的。”[9]

其实，古“三分损益法”已具备一定的科学依据。“三分损益法”是一种生律方法，亦可称其为“五度相生法”，所得律制又可称为“ 五度相生律”[10]（circle-of-fifths system），这种律制是应用谐音列[11]中三号谐音与二号谐音的比例（五度律纯五度）生律。继而《吕氏春秋》中有完整十二律相生的记载，相生法如下，

“黄钟生林钟，林钟生太簇……三分所生，益之一分以上生；三分所生，去其一分以下生。黄钟、大吕、太簇、夹钟、姑洗、仲吕、蕤宾为上，林钟、夷则、南吕、无射、应钟为下。”[12]

依此文献记载，“黄钟”为上，“林钟”为下，“黄钟生林钟”则是通过“去其一分”而得，此与“三分而益之以一”生“徵”（《管子·地员篇》）不同。

现根据《吕氏春秋》记载，将其中律名、生律顺序、长度比制表如下[13]

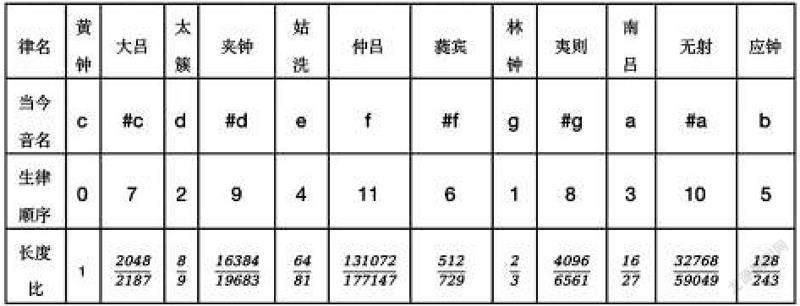
表1

其中，蕤宾、大吕二律经连续两次上生而得，即蕤宾由应钟之长度比128/243×4/3 而得，大吕由蕤宾之长度比512/729×4/3 而得，这是该生律法中最为显著的一个特点。从这一特点中可以得知，《管子》中“黄钟小素之首”宫音“三分而益之以一”（即乘4/3，按《吕氏春秋》所述，“益一”视为“上生”）生徵音与《吕氏春秋》中黄钟“下生”（即乘2/3）生“林钟”所不同的原因之一在于可以保证十二律保持在同一个八度之内，通过该记载可以推论此时并无涉及到“‘黄钟还原这个命题。”

二、“黄钟还原”之探索

中国乐学以律学为基础，是一门与音乐实践紧密关联的学科，而中国古代近两千年的律制探索正是为了解决旋宫问题而展开。三分损益相生十二律是中国古人乐律学研究的智慧结晶，不过经三分损益法相生十二律有其自身难以调和的矛盾——“黄钟”无法还原，即从“黄钟”相生到“仲吕”时则无法还生到“黄钟”本律。究其原因，在于十二律内部相邻两律之间音分并不相同，存在大半音（114 音分）、小半音（90 音分）两种半音。

（一）“黄钟不得还原”之律学分析

律学是研究乐音运动规律的学问，律学分析则是用数理方法进行具体研究，包括对音程、音高等的计量运算。关于音程的计算方法，包括频率比、音分值、八度值、对数值等几种方式，其中频率比的计算方法是基础，音分的计算方法则可以直观了解音程之间的距离，从而判断音程大小。上述方式中，除了频率比之外，其余几种计算音分数的方法则涉及对数原理，运用方法如下：

在五度相生方法中，欲求高五度的一律，则乘3/2，继而相生，则乘其二次方，即乘（3/2）²，以此类推，而后作八度移动，移低几个八度则除以2 的几次幂（即2x）。黄钟本律相生至仲吕继而相生回不到黄钟本律的原因在于多出24 音分（“最大音差”），即从黄钟相生12 次只可得变律黄钟，此律距离黄钟出发律7 个八度，生律数理表达式为：（3/2）¹²/2⁷，其音分计算方法为：

log₁₀（（3/2）¹²/2⁷）×1200/log10²

最终得出约24 音分，相较于平均律半音之五分之一强，这也是黄钟相生十二次后无法还原至黄钟本律的原因。

实际，黄钟C 音[14]相生最后得到的音为＃B 音，在十二平均律的律制下＃B 与C 等音，但在五度相生律中，二者并不同。本质上则是由于五度律大全音（C—D）之间存两个升降音的差别使然，这是五度相生律本身存在的问题。

在数理计算时，前人曾提出“对数值……各值小数点后有五位。实际除了作极精细的研究外，用小数点后三位即可，第四位四舍五入。一般可以把小数点略去……”[15]不作细究，难以发现以小数计算易出现的问题。在计算过程中，过早将分数化为小数，以及提前采用常数K 的小数形式，会涉及小数点后位数的取舍需要，如计算C 至＃C 与C 至bD 的音差时，若在分数转化小数的计算过程中每一步都采取小数点后四位数时，可以得出约22 音分（即“普通音差”，但五度律大半音与小半音音差为“最大音差”24 音分）的结果，采取小数点后三位时则得到约24 音分（即“最大音差”），采取小数点后两位数时，只能得到约17 音分的结论，结果更差矣。因此，为避免误差过大，最佳方式为整个运算过程保持使用对数计算规则，直至最后无法简化的情况下采用小数计算，如此便可以更清晰地得出应有的结果。

着实，乐律学研究涉及到严谨的数学方法，但“在乐律学的表述和探讨中，现有的方法也不够理想。”[16]所以启示着音乐学人既要掌握基本的数学方法，也需改进固有的方法。

（二）律制探索

由于五度相生律本身存在的矛盾使得黄钟无法还原，从而影响“旋相为宫”，因此，历代音乐家和律学研究者为了音乐实践的需要展开长期探索，其方法主要包括两类：一类是采用五度相生法继续生律，如京房六十律、钱乐之三百六十律；一类是在十二律内部进行调整，使得最后一律可回归出发律。

汉代京房是我国最早发现黄钟相生十二次无法还原黄钟本律者，他将该律取名“执始”，其与黄钟相差24 音分，从而京房在三分损益十二律的基础上，力求“黄钟自冬至始，及冬至而复”（《后汉书·律历上》），因此“推此上下，以定六十律之实”相生至六十律“南事”。在该律制中，由黄钟相生53 次至“色育”律时，其音分已十分接近黄钟律，二者仅差3.615 音分（亦称为“京房音差”）。而京房继而相生至第六十律“南事”为的是“还相为宫”，该“宫”指的是“他前所列举自黄钟至蕤宾七声那样所组成的一‘均。”[17]

但该律制难以应用于实践当中，甚至京房六十律被认为是“从来没有起过什么积极作用”，“若说京房六十律能有什么作用的话，则它所起的，只能是消极的作用。”[18]从律学研究角度而言，京房发现“最大音差”并以严密的逻辑思维作数理探索，此确实为以后的律学发展奠定了基础。

在京房六十律的基础上，延承三分损益法继续相生者后继有人，《隋书·卷十六·律历志》载，

“宋钱乐之衍京房六十律，更增为三百六十，梁博士沈重，述其名数。”[19]

南北朝时期，钱乐之继续运用三分损益法，在京房六十律的基础上继而相生至三百六十律，从乐律理论研究角度来看，该律制达到了音律细分的最高程度，其“一日”之音差较“京房音差”更小，仅1.845 音分。后期，梁朝沈重同样发明三百六十律。

与钱乐之同时期的何承天则认为“上下相生，三分损益其一，盖是古人简易之法”，认为“京房不悟，谬为六十。”（《隋书·音乐志》），由此创制“新率”。具体方法则是在十二律内部进行调整，即先通过三分损益法求得“仲吕还得黄钟”之实数174762 2/3，其比黄钟之（3¹¹）177147 短2384 1/3，后将其差数平均分成12份，依此加至各律，而后除以“一而九三之”19683 得各律的振动体长度，该律被学界称为“十二平均律的先驱”[20]。从本质而言，何承天新律之所以不是真正的十二平均律在于其是将振动体长度的差数十二等分而不是将振动体的频率比数十二等分。

自何承天新律之后，更加接近十二平均律且更具物理意义的律制为王朴律。不过，近代学者对王朴律曾有不同见解，有认为王朴律为“纯律”者，如楊荫浏、吴南薰，亦有认为王朴律为“纯正音阶律”者，如王光祈。

王朴为五代时期乐律学家，其原理采用的依然是三分损益的基本方法，但王朴律之所以被称作“新法”，原因正在于他改变了损益比率，促使该律制在一个八度内进行调整。《旧五代史·乐志》所载，

“……（王朴）乃作律准十三弦。宣声长九尺，张弦各如黄钟声。……第十三弦四尺五寸设柱，为黄钟之清声。”[21]

其中第13 弦在四尺五寸处设柱，首先框定黄钟与黄钟之清声的弦长关系，体现出王朴已十分明确二律的倍半关系，是一种突破性尝试。

该律制按照三分损益“隔八相生”的基本方法具体体现在定一弦为黄钟，其余琴弦设柱顺序依次为第八、三、十、五、十二、七、二、九、四、十一、六弦，现按照其生律顺序制表如下

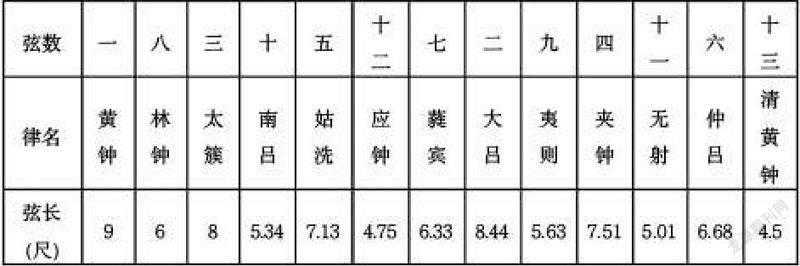
表2

总体来看，其律制明显延承了三分损益的基本方法，但不像京房等采取相生法增加律数，而是在八度内部对弦长有所调整。由于数据之间的差异，促使近代学者们对王朴律属于何种律制展开争鸣探讨。比较上述数据与标准三分损益法的弦长数据可以发现，近代学者计算三分损益律弦长时，仲吕、清黄钟为6.66 尺与4.44 尺，但需要注意的是只有在计算过程中保留小数点后至少三位数时可得出该结果，若按照保留小数点后两位运算，则得出6.65、4.43 的结论。

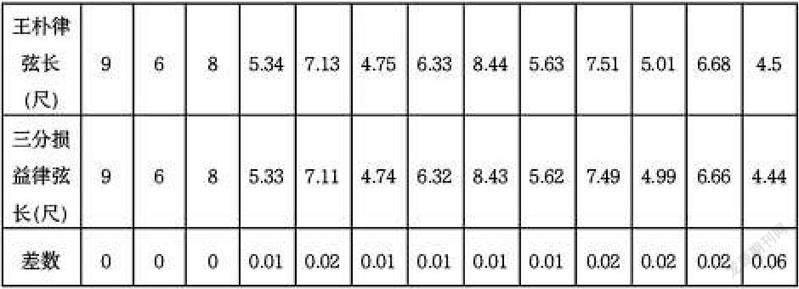
表3

通过上表可知，王朴律从黄钟律出发，经两次相生所得律之弦长与三分损益律同，但从南吕开始，两种律制弦长出现差额，包含0.01 尺、0.02 尺。而这种差额的出现，引起近代学者关注并求解。引起差额的出现实际是由于损益比率的不同，但由于王朴并没有明确说明其损益比率，所以明确比率成为研究王朴律的第一要务。截至今天，分别有学者提出王朴律可能在三分损益法的基础上，将分母三减去1/500、3/500 进行损益[22]；用“朴质的最佳逼近法”[23]求得比率500000/749785；计算南吕、姑洗两律时用“跃迁”[24]方法求出分母缩小4/900 的比率等几种方法。其中采用“跃迁”方法计算所得更符合王朴律。通过分析可知，王朴律旨在于“旋迭为均”，实质已经在向十二平均律进一步靠近，且其方法对朱载堉有所启发。

最终正式解决“黄钟还原”，可使得十二律“旋相为宫”的是明代乐律学家朱载堉，其曾高度肯定王朴“足以度越诸家”。朱载堉因王朴启发作进一步探索，在《律历融通》中提出变2/3 为500000000/749153538，变4/3 为1000000000/749153538 的比率上下相生求得各律，此外仍在《律历融通》《律学新说》《律吕精义》提出不同的计算思路，其中《律吕精义》将具体算法列出，“是故新法不用三分损益，别造密率……”（《律吕精义》）最终创设“新法密率”，创立了真正的十二平均律。由此，历经两千余年的乐律学难题告一段落。

此外，在历史探索过程中，亦有刘焯律、蔡元定十八律等律制，但刘焯混淆了频率比与频率差的概念，因此其律制犯了根本性错误，而蔡元定律制实则同京房六十律前十八律。

三、三分损益“黄钟无法还原”之本质

前文谈到，三分损益律制有其不可调和的矛盾，其中包含两种半音，大半音（114 音分），小半音（90）音分，从而导致从黄钟出发律无法还原至黄钟本律，这是通过数理计算得出的结论。京房、钱乐之等人采用三分损益法继续相生，虽音分数得到了越来越小的差额，但终不如朱载堉之十二平均律般可使黄钟完满还原，十二律完满旋宫。三分损益本质如何，可数理探得：

由五度相生数理原理得出，生律式可以3ⁿ/2^m表示，通过对数原则计算音分数，最终可得算式：（nlog10³-mlog10²）×1200/log10²，即（n（log10³）（/ log10²）-m）×1200，因為（log10³）（/ log10²）为无理数，n、m 为有理数，该算式最终只可得无理数，所以从数理本质来看，黄钟律出发，无论生律多少次也无法还原黄钟本律，只可无限缩小差额。

“黄钟不能还原”“十二律不得旋相为宫”的历史难题自三分损益法始，自朱载堉“新法”终，历时近两千年。京房首先发现该问题且首次运用数理计算方法寻求解决方案，为后来的律学研究者奠定基础，无论是延承三分损益法继续生律者，还是改变生律思路在八度内调整者，一定程度上皆得益于京房的启发。虽然三分损益法从本质上而言是无法完成黄钟还原这一使命，但王朴律、朱载堉改变比率的思路亦得益于三分损益。总体而言，将无形之音，转化为有形之数，进而实现音之数理探索，形成中国传统乐律学之完备理论体系，充溢着先人的伟大智慧！

（责任编辑 于洋）