压缩载荷作用下多孔复合材料力学关系的数理推演
2023-05-16刘培生
刘培生
(北京师范大学 核科学与技术学院 射线束技术教育部重点实验室,北京100875)
0 引言
在很多应用中,多孔材料需要同时发挥其结构和功能的双重作用[1-2]。因此,既要利用其功能属性,又要求其具有一定的力学性能。功能属性往往是利用其内部孔隙表面和空间,由此大力发展了三维网状通孔结构的多孔材料。例如,在需要比表面积大、透过性好、吸声性佳、换热散热能力强、电磁波吸收性优、阻火阻焰等应用场合,都要将多孔材料制造成通孔结构[1]。三维网状结构的高孔率泡沫金属正是这样一类多孔材料,目前已成为优秀的电极材料、催化材料、换热材料和生物材料等工程材料。在这些工程材料中,多孔金属体既是起支撑作用的骨架,其内部孔隙又提供了电极过程、催化过程、热交换过程和生物组织生长过程等功能实现过程的有效场所。
三维网状制品是多孔材料结构形态中应用最为广泛的结构类型。该类材料内部孔隙表面的优化即其孔棱表层的优化,可进一步改善其使用性能。例如,文献[3]为提高多孔金属制品的应用性能,利用分层电沉积技术,在三维网状多孔铜的基础上让金属铜孔棱覆加镍层,制备出多孔Cu/Ni复合材料。所得多孔复合产品的抗压缩强度和杨氏模量得到明显提升,单位体积吸能能力更是得到显著增大。文献[4]在泡沫钛表面制造了生物活性层,以提高其应用于人体植入材料方面的生物相容性。文献[5]为了解决多孔硅表面悬键降低发光效率的问题,利用脉冲激光沉积(pulsed laser deposition,PLD)技术在多孔硅衬底上沉积一层ZnS薄膜,形成的Si/ZnS复合结构提高了多孔体系的发光效率,等等。可见,这类以开孔泡沫金属(或开孔泡沫陶瓷)为基本骨架,内部表面施加覆层形成孔棱呈复层结构型式的网状多孔复合材料,在一些场合具有重要的用途。本文即探讨这类材料的力学关系,介绍其有关力学关系的推演以及获得的结果。对于所有工程材料来说,拉压性能都是一项最为基本的力学性能。网状多孔复合材料作为一种比较新型的工程材料,因此有必要从其结构类型的整体意义上,探讨此类材料最为基本的力学性能,即压缩性能。此类结构的多孔材料工作还比较少,目前没有发现对其在各类载荷形式作用下开展的一般性力学关系研究。本文即尝试开展这项工作,并着眼于此种多孔复合材料最基本的压缩行为。
1 分析模型
对于具有网状结构的三维同性多孔材料(参见图1),可建立一个均匀分布的八面体结构模型(参见图2)来简化分析其拉伸和压缩行为[6-9]:这种结构的材料由均匀分布的固体孔棱连接构成,这些固体孔棱可视为规则地按照立方体对角线的方式进行连接,因而形成大量的密积体心立方式八面体孔隙单元。在该模型中,结构单元只由一类孔棱所构成,而且建构结构单元的所有孔棱都是完全等价的[6]。八面体孔隙单元在3个相互垂直的方向上规则地分布,亦即在八面体的3个轴线方向上规则地分布,因而实现了孔隙单元在空间上的完全填充(即孔隙单元形成了密堆积而充分填满了空间),由此构成整个多孔体。

图1 代表性网状结构多孔材料宏观形貌
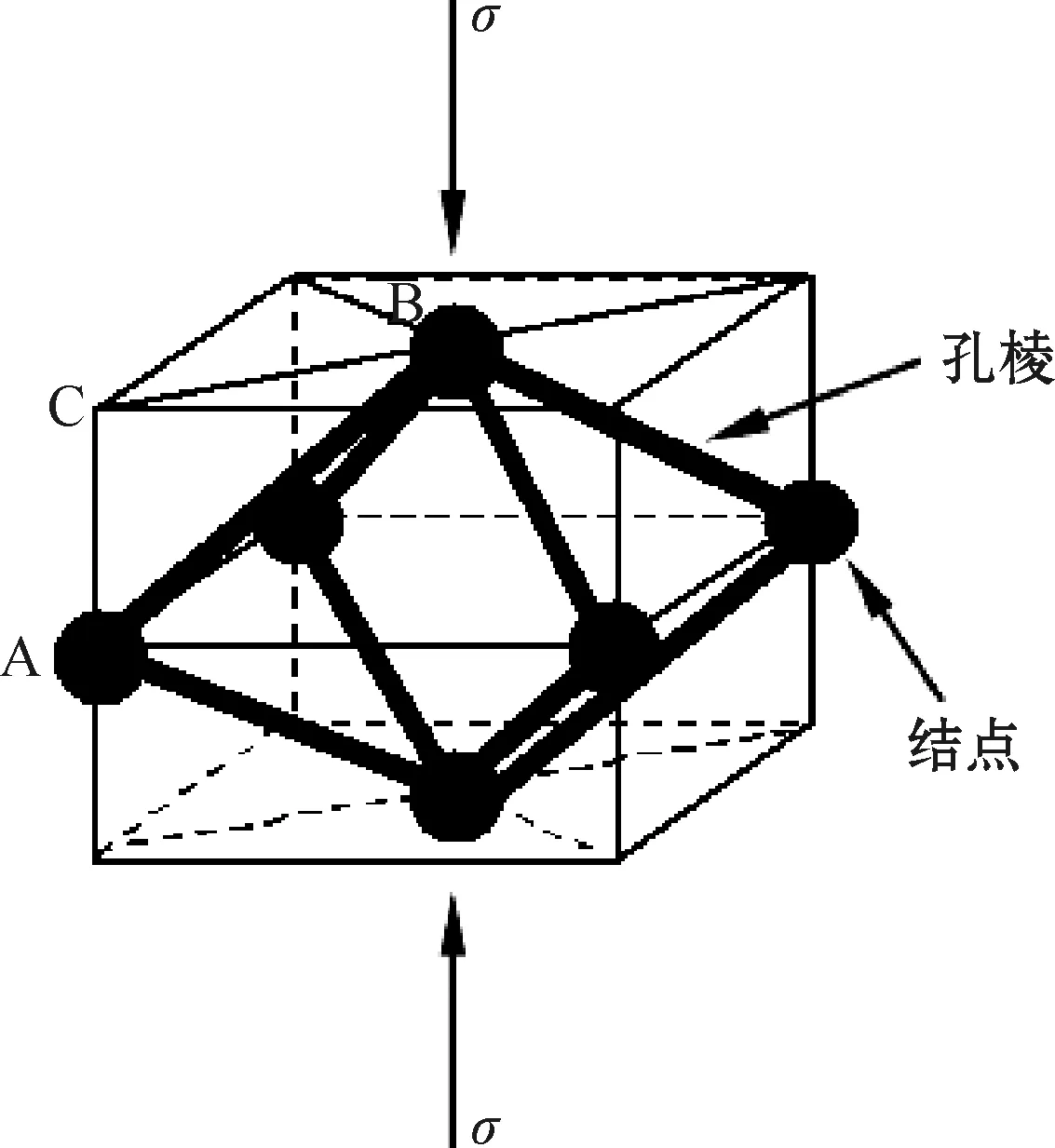
图2 各向同性的网状结构多孔材料在压缩载荷作用下的八面体单元
图2显示,所有孔棱都是立方体中心和顶点之间的连线,因此意味着它们在结构上都是等价的[6]。每个孔隙单元都由这样的8条孔棱构成,每条孔棱都由3个轴线相互正交的孔隙单元所共享。例如,图2中的孔棱AB(这里B点是立方体的中点,A点是立方体的顶点)同时参与了3个以B点为顶点的八面体孔隙单元的构成。第一个单元的轴线位于外加载荷的方向,见图2中的主单元;第二个单元位于主单元的左上侧,第三个单元位于主单元的前上侧。这些轴线相互垂直的八面体单元形成了相互之间的密堆积,从而填满了空间。按照这种方式,本模型实现了均匀结构和三维同性的总体特征,这样的孔隙单元和结构单元两者是完全统一和充分一致的。
在本工作研究对象中,此类多孔材料为开孔泡沫金属(或开孔泡沫陶瓷)基体的内部表面施加覆层后形成的网状多孔复合材料,其孔棱呈复层结构形式:即一种材质组成的外层即壳部(施加覆层的材质),包裹住另外一种材质组成的内芯即芯部(开孔基体的材质),由此形成了本工作要研究的多孔复合材料。
2 分析方法和相关参量
2.1 分析方法
在多孔材料内部,结点的承载能力一般高于孔棱。因此,当多孔材料承受外加载荷时,失效往往发生在孔棱上。为简化起见,可将这些孔棱视为细圆柱梁(见图3)。当孔棱内部产生的最大正应力(σmax)即最大拉压应力达到对应致密材质的许用正应力[σ]时,多孔体将发生失效。此处许用正应力相当于对应的拉压强度(σ0)。此时作用在多孔体上的外加名义压缩应力(σ)即可视为该多孔材料的压缩强度。这里要考虑的是孔棱由两种不同材质构成的网状多孔复合材料,其中的复合孔棱包含孔棱芯部和孔棱壳部两个部分(图3(b))。
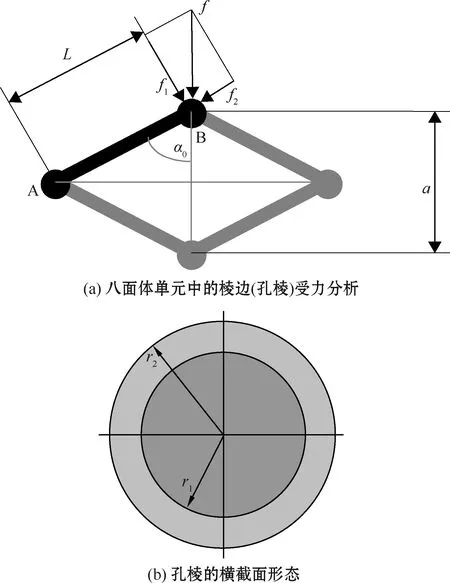
图3 网状结构多孔复合材料在单向压缩状态下的孔棱分析示意图
基于上述模型,大量八面体单元组成的规则性十字正交排列构建成多孔体[6]。当多孔体受到外加载荷时,其内部这些均匀排列结构的单元也将均匀地受到载荷作用。由此,可选用一个单一的孔隙单元作为代表来进行分析,并将该单元八面体的中心对称轴考虑为处于多孔体压缩方向(见图2中的箭头方向)。本模型中的孔棱在结构上是等价的,在承受载荷方面也是等价的,因此任意一条孔棱都可用来表征其他孔棱的特性。可抽取某一孔棱(AB)来进行分析(参见图2和图3)。为推导简便起见,对于受到单向压缩载荷的多孔体,不妨将其分析的孔棱(AB)视为侧结点(A)固定而顶结点(B)受到外部载荷的细圆柱形悬臂梁。当然,推演也是在材料力学“小变形假定”的前提下以及弹性范围内进行。
2.2 相关参量
首先,可从几何关系得出八面体中孔棱的长度和半径。设包容单元八面体的立方格子边长为a(大致相当于多孔体的孔径尺度),孔棱长度为L(参见图3(a));孔棱的芯部半径和壳部半径分别为r1和r2(参见图3(b))。对应地,设孔棱外部的连续孔隙在复合前后的孔率分别为θ1和θ2。于是,我们可以通过几何计算得到相关的几何参量。另外,根据这些几何参量还可进一步得出孔棱的惯性矩等。
1) 孔棱长度 (L)
在八面体单元的几何模型中,8条孔棱的长度近似为
(1)
2) 孔棱半径 (r)
每个单元立方体(边长为a)包容一个八面体单元,含有8条孔棱,有其近似的体积关系如下[8]:
(2)
(3)
类似地,有
(4)
(5)
3) 孔棱的惯性矩(Iz)
根据工程力学理论,孔棱芯部的惯性矩(Iz1)和孔棱壳部的惯性矩(Iz2)可计算如下:

(6)
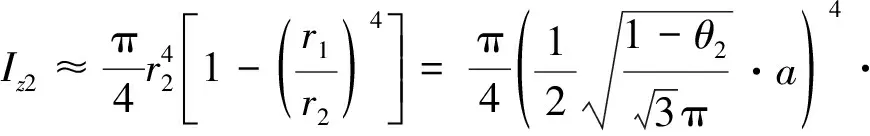
(7)
3 数理关系推演
3.1 基本关系推演
对于由密堆积八面体单元构成的网状多孔材料,每条孔棱都由3个这样的单元所共享。当名义压缩应力为σ的单向载荷施加到多孔体时(参见图2),作用在八面体单元上的载荷力即为
F=a2·σ
(8)
而作用到每条孔棱上的作用力将是
(9)
式中:a为对于高孔率多孔材料大致相当于多孔体的孔径尺度,近似计算时可用多孔体复合前测出的孔径代替。
图3(a)是八面体单元中4条处于相对位置的孔棱组成的平面图,其中α0为孔棱与八面体单元中心对称轴之间的原始夹角。从图2和图3(a),可得出作用于孔棱(AB)结点B上的力f的横向分力为
(10)
这样的受力分析方式,根据已有研究工作(参见文献[7,10])表明是可行的,获得的理论结果为实验数据所验证,具有良好的实用性。诚然,上述结点B会同时受到与孔棱AB对称的其它孔棱的支撑,但通过如下处理即可化解这个问题:将结点B上方4棱(参见图2)与其下方4棱视为两个不同的受力作用整体,上方4棱通过结点B将外加载荷传递到下方4棱;将其上方4棱对下方4棱的作用合成为一个力(合力)后,再平均分配给下方4棱。这样来处理,就可从式(8)得出式(9)所表征的作用到每条孔棱(包括孔棱AB)上的作用力,进而得到式(10)所表征的作用于孔棱(AB)结点B上的横向分力。
将孔棱(AB)视为侧结点(A)固定而顶结点(B)受到外加载荷的细悬臂梁,则作用于孔棱(AB)的最大弯矩可通过式(1)和式(10)得出:
(11)
设此处孔棱的曲率半径为ρ,棱芯材质和棱壳材质的杨氏模量分别为E1和E2,则此时孔棱芯部和孔棱壳部与孔棱截面中性轴距离为b(变量)处的正应力σ(b)可分别表示为(在构件属于小变形条件下,孔棱的曲率半径ρ也相对具有较大的值):
(12)
(13)
式(12)和式(13)即离孔棱中性轴距离为b处孔棱内部的正应力。
又设此处孔棱芯部和孔棱壳部承担的弯矩分别为M1和M2,则
M1+M2=Mmax
(14)
由式(12)、(13)代入得
(15)
式中:A1和A2分别表示孔棱芯部和孔棱壳部的横截面范围及其面积。由式(15)得
(16)
(16′)
(17)
(18)
3.2 复合多孔体的安全承载关系
由式(12)、(13)和(18)即可直接得出多孔体的安全承载关系,即孔棱芯部和孔棱壳部上产生的最大正应力σ1max和σ2max同时小于其对应材料的许用正应力[σ1]和[σ2],这里相当于对应的拉伸强度和压缩强度(σ01和σ02):
(19)
(20)
将式(3)、式(5)~(7)、式(11)代入式(19)、(20),得:
(21)
(22)
(23)
和
(24)
分别修正为
(25)
和
(26)
式中:k为修正系数,是复合体的材料常数,涉及复合体中泡沫金属物质种类和制备工艺以及复合物种、复合工艺等。

σ1max(r1)≈
(27)
σ2max(r2)≈
(28)
式中,K类似于上述常数k,亦为复合体的材料常数。
3.3 复合多孔体的整体承载强度
当孔棱芯部产生的最大正应力σ1max达到芯部材料的许用正应力[σ1],或者孔棱壳部产生的最大正应力σ2max达到壳部材料的许用正应力[σ2]时,施加于复合多孔体的外加载荷(σ)即对应于孔棱芯部控制的复合多孔体整体的抗压强度或孔棱壳部控制的复合多孔体整体的抗压强度。因此,根据式(27)和(28),可通过公式变形直接得到:
1) 由孔棱芯部优先破坏造成的整体失效而对应的复合多孔体承压强度
σ≈
(29)
2) 由孔棱壳部优先破坏造成的整体失效而对应的复合多孔体承压强度
σ≈
(30)
4 讨论
在关于多孔材料结构和性能方面的理论中,基于立方体孔隙单元的Gibson-Ashby模型(GA模型)理论最富于引领性和经典色彩[10]。但是,该模型理论的一些特点导致其应用过程中出现困难。这些特点体现在孔隙单元的非密积性、棱柱结构的不等价性、孔棱结点的不等同性、外力作用下不同棱柱的受力状态差异性等方面[6,11-12]。另如比较有代表性的Kelvin模型(十四面体结构模型),还有三棱柱结构模型、四棱柱结构模型、六棱柱结构模型、菱形十二面体模型等,也都存在着与Gibson-Ashby模型某些类似的特点,如结构单元中的孔棱状态不等价等[6,11-12]。因此,这些模型不能或不便进行有关性能分析及其数理关系推演。例如,对于上述结构型式的多孔复合材料,这些模型在其压缩性能的分析推演方面,即难以像本文的八面体模型那样方便地施展,甚至是不能进行这样的分析推演。
任何理论模型都是在一定程度上对实际状态的抽象和综合概括,其目的都是在尽量简化的基础上简捷而方便地表征出实际状态的有效特征和性能行为[6]。同样,要评价多孔材料结构模型的优劣,关键也是要看其是否能够从相应模型出发,获得符合多孔材料实测性能结果的对应实用性数理表征,而且数理关系推演过程要尽量便捷、实际应用简易。在前述已建立的多孔材料理论模型中,除Kelvin模型外,其他结构模型对网状多孔材料实际结构的偏离程度,都要大于本文作者提出的八面体结构模型(参见文献[10]和[6])。但本八面体结构模型的优越性,根本还在于其孔隙单元中孔棱结构状态的完全等价性。这是包括Kelvin模型在内的所有模型理论都无法达到的,尽管Kelvin模型比本八面体模型更接近于网状多孔材料的实际结构。也正是这一优越性,使得本八面体结构模型在孔棱受力分析的可行且便捷方面,可以完胜包括GA模型和Kelvin模型在内的其他模型理论(参见文献[8]、[11]和[12])。在本文所考虑的压缩载荷作用下,只有八面体模型理论能够实现孔隙单元中所有孔棱的受力状态可以完全等价,从而实现简便而可行的推演并获得希望的结果。对于本文所论多孔复合材料的对应力学关系推演,其他模型理论更是难以企及。作者系列的模型理论工作(参见文献[6-9]),其主要目标是希望通过调节主要结构参量即孔率,来达成产品性能控制特别是产品综合性能优化设计的目的。为此,需要建立产品性能与其孔率作为变量条件下的数理关系[6]。在这个方面,文献[7]介绍了对本八面体模型理论的系列实验验证工作,用企业生产线制造的实际产品的对应数据,证明了该模型理论的良好实用性。综上可见,作者提出多孔材料八面体模型理论,意义十分明显。作者后期还将开展更多的相关探讨,进一步夯实本模型理论所得性能数理关系的验证工作。在此基础上,将该模型理论更多地推广到相关部门以服务于实践。希望在不远的将来,本模型理论可以广泛地实际运用于网状多孔材料产品的生产工艺设计和性能综合优化设计。
本文是作者在自提多孔材料八面体模型理论的基础上,进一步建立文中所述多孔复合材料在压缩载荷作用下的力学分析模型,巧妙地运用几何关系和工程力学的有关知识,从而推演出此类多孔复合材料在对应载荷型式下的力学关系。本文的主体内容即是推演,推演过程中的所有数理关系均基于有关数理分析,整个推演过程围绕所述多孔复合材料而进行。可见,本工作系作者系统地推演文中所述多孔复合材料在压缩载荷作用下的力学关系:在推演中,关键是找出有关量与量之间有机的相互联系并建立有关力学方面的数理关系,从而通过推演去推出新知。文中呈现了作者自成体系的数理分析工作,工作结果揭示了多孔复合材料在压缩载荷作用下未知的力学关系规律。当然,任何模型理论都是在已有知识体系的基础上,通过创立者的分析推演等创造性劳动,得到新知和揭示未知规律。如果创立者不能建立其有效的联系和做出特有的推演,就无法得到前人没有公布过的新知和未知规律。因此,模型理论工作具有其独特的研究意义。
另外,本文只是介绍了压缩载荷作用下多孔复合材料的力学关系推演以及获得的对应力学关系结果,而没有作者自己在有关实验数据基础上的相关数理分析验证工作。后期我们将制备系列的网状多孔复合样品并进行其系列的有关测试,获取系列的实验数据,在此基础上对本文所得力学关系进行数理分析验证。这项工作将尽快择机开展,到时将形成本文的姊妹篇。
5 结束语
目前,网状泡沫金属的应用差不多覆盖了原多孔金属的所有应用领域并有所拓宽,如用于各种过滤器、流体混合器、热交换器、电磁屏蔽材料、催化剂及其载体、各种高效电池电极、电合成和重金属回收等的电化学过程阴极、生物材料和环保材料、复合金属材料和宇航工业中的某些结构材料等。因此,对该类多孔材料的结构性能以及优化应用设计,都值得进一步重视。由于多孔材料在工程应用中可能涉及其物理、力学等多方面的性能,不同的性能要求对材料参数的选择是不同的。为优化结构性能和扩展应用范围,即需要发展复合结构的多孔产品。因此,需要对材料性能进行评估,选取合适的材料参数。本文即是在作者所建立的多孔材料结构模型的基础上,衍生拓展出孔棱为复层结构的性能分析推演模型,建立其压缩性能指标与结构参数的数理关系,以此为该类多孔复合材料制品的性能设计提供参考。
