钝体火焰稳定器后燃烧不稳定数值模拟

仝照旭，韩启祥

（南京航空航天大学能源与动力学院，南京 210016）

0 引言

随着航空发动机向高推重比、高可靠性的方向发展，其加力燃烧室内部的燃烧不稳定现象备受关注[1-3]。钝体稳定器作为最通用的火焰稳定器之一，广泛应用于冲压发动机及涡喷发动机加力燃烧室中[4-5]。钝体稳定器后燃烧不稳定现象极易受来流条件的影响，随着燃烧室来流温度升高，来流马赫数加大，钝体稳定器后发生燃烧不稳定的几率大幅增加，给航空发动机高效、稳定运行带来重大隐患。因此，燃烧不稳定现象自从被发现以来，广泛受到工程设计者的关注。但由于燃烧不稳定现象受到多种因素相互作用[6-8]，如化学反应，湍流流动等，且涉及热力学、传热学、声学、流体力学等多个学科相互交叉，一直难以解决。

国内外学者们通常采用数值模拟对燃烧不稳定现象开展研究。Matthew 等[9]针对轴对称火焰的纵向振荡问题，采用2 维模型得到的计算结果与试验结果吻合程度较好，相较于3 维模型极大简化了计算资源；刘卫东等[10]应用改进的PISO 算法对液氢/液氧火箭发动机径向燃烧不稳定现象进行数值模拟，结果表明对该型发动机声腔应用谐振器阻尼后，压力扰动波最终被系统抑制；朱旻明等[11]通过U-RANS/PDF 方法对钝体稳定器后漩涡脱落特性进行分析，相对准确地预测了稳定器尾缘涡脱落频率，但发生燃烧不稳定时稳定器后的局部雷诺数较高、特征时间较短（一般在μs量级），其流场具有很强的非定常特性及3维效应。这些因素的限制使得国内外关于加力燃烧室燃烧不稳定的研究工作主要围绕时均特征展开，导致对燃烧不稳定的瞬态特征和作用机理缺乏系统及深入的认识。

本文基于商用软件Fluent，采用大涡模拟（Large Eddy Simulation，LES）方法对带钝体稳定器的模型加力燃烧室进行3 维热态数值模拟。通过改变来流温度、来流马赫数、当量比3 种影响燃烧的关键因素来分析其对钝体稳定器后燃烧不稳定的影响。

1 研究对象与数值计算方法

1.1 几何模型

选择加力燃烧室中常见的钝体稳定器，尺寸如图1 所示。其主要参数为：槽宽D=45 mm、顶角α=30°、顶角半径R=12 mm、壁厚b=3mm。大涡模拟对网格精度和计算资源要求极高，有必要对计算域进行简化。本文采用Euqenio[12]对带钝体稳定器的模型燃烧室进行简化：对钝体高度方向取45 mm（1D），简化后钝体高度方向2 个面取平移周期边界，3维计算域如图2所示。

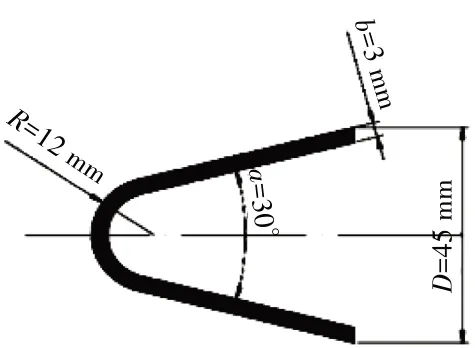
图1 钝体稳定器尺寸

图2 3维计算域

计算域在笛卡尔坐标下表示，选取钝体稳定器尾缘中心为原点，x方向为长度方向，y方向为宽度方向，z方向为高度方向。3 维计算域尺寸为750 mm×136 mm×45 mm。

1.2 网格划分与独立性验证

采用ICEM 软件划分计算域结构化网格。为了精准捕捉钝体稳定器壁面的流动分离现象，对其周围划分边界层网格，钝体稳定器壁面第1 层网格高度Δy≤0.02 mm，边界层网格增长率为1.2，满足LES 对于近壁网格的要求（y+～1）。整体网格划分从钝体稳定器出发，向周围均匀过渡。网格总体质量≥0.85，网格最小正交性≥0.7。

对冷态流场选取3种数量的网格进行无关性验证：mesh1（41.8万）、mesh2（117.2万）、mesh3（240.1万）。3种网格稳定器尾缘x=15 mm处时均流向速度如图3所示。从图中可见，当网格量从117.2万增大到240.1万时，由于网格量改变造成的计算误差基本可以忽略，综合求解精度以及计算成本选取117.2万（mesh2）进行数值计算。中心截面网格剖分如图4所示。

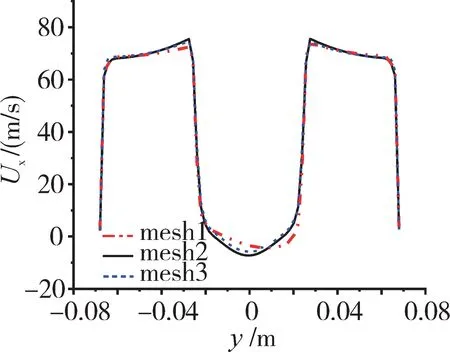
图3 3种网格稳定器尾缘x=15 mm处流向时均速度

图4 中心截面网格剖分

1.3 计算模型与算例验证

1.3.1 计算模型

湍流模型选择LES 模型，其中亚格子模型选择Wale 模型。因为Wale 模型是一种类似Smagorinsky模型的代数模型，但克服了Smagorinsky 模型耗散偏大的缺陷且能够相对准确地预测层流到湍流的过渡。

离散相模型选择非稳态颗粒追踪，离散相颗粒选择适合液体燃料的液滴（Droplet），阻力系数Cd选择动力学曳力模型（Dynamic Drag Model）。离散相模型普适性好，几乎适用所有的流动情形，二次雾化选择波动破碎模型（Wave Break Up），喷嘴类型选择实心喷嘴（Solid Cone）。

在钝体稳定器前150 mm 处垂直来流方向设置6 个喷嘴来提供燃烧所需的燃料，供油位置（黑色圆圈）如图5所示。

图5 供油位置

燃烧模型选取有限速率/涡耗散模型（Finite-Rate/Eddy-Dissipation，FR/ED），该模型结合了Arrhenius 公式和涡耗散方程，避免了Eddy-Dissipation 模型出现的提前燃烧问题，并且结合了动力学因素和湍流因素，广泛用于航空发动机燃烧室的燃烧模拟。采用航空煤油2步总包反应[13]。

本文采用有限体积法求解纳维-斯托克斯方程（Navier-Stokes，N-S）方程，压力和速度耦合采用SIMPLE 算法，压力项采用2 阶迎风格式，动量项采用中心差分格式，时间离散采用中心差分格式。为保证计算精度，时间步长选取1×10-6s。

1.3.2 标准算例验证

本文通过标准算例来验证选择的计算模型能否准确预测稳定器后的流场、气流的脉动频率以及火焰的分布形态。其中Giacomazzi 等[12]和Fureby[14]的研究对象为闭口钝体稳定器，Barry 等[15]的研究对象为开口钝体稳定器。

1.3.2.1 稳定器后流场结构对比

本文与Giacomazzi 的模拟结果的对比如图6 所示。从图中可见，二者在稳定器后流域的漩涡数量均为6个。从左向右前3个漩涡在流域中的位置几乎一致，后3 个漩涡的空间分布稍有差异，但总体分布位置相似。故本文的计算方法可以相对准确地预测钝体稳定器后的流场结构。

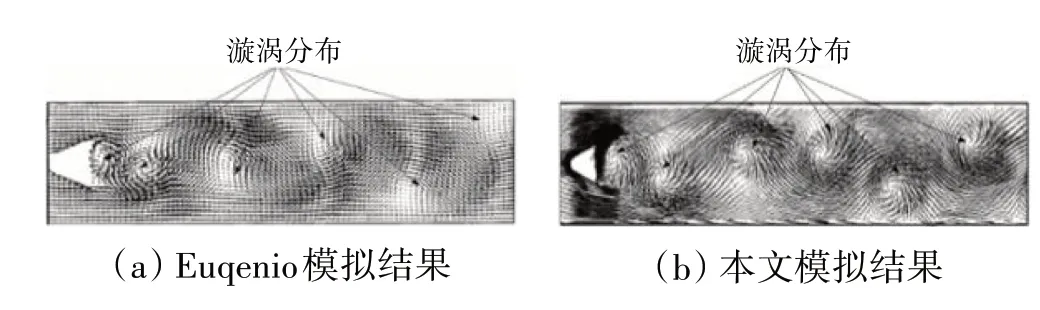
图6 本文与Euqenio模拟结果的对比

1.3.2.2 稳定器后监测点的脉动频率

稳定器后监测点脉动频率见表1。从表中可见，本文的计算结果与Fureby的试验结果的误差为5.7%，且 与Giacomazzi 的模拟结果的误差相差较小。说明本文的计算方法可以相对准确地预测钝体稳定器后气流的脉动频率。

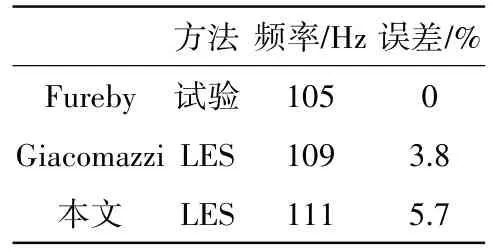
表1 稳定器后监测点脉动频率

1.3.2.3 稳定器后火焰形态

钝体稳定器尾迹火焰形态如图7 所示。从图中可见，本文的模拟结果与Barry 等[15]通过高速摄影得到的稳定器后火焰形态的一致性较好。

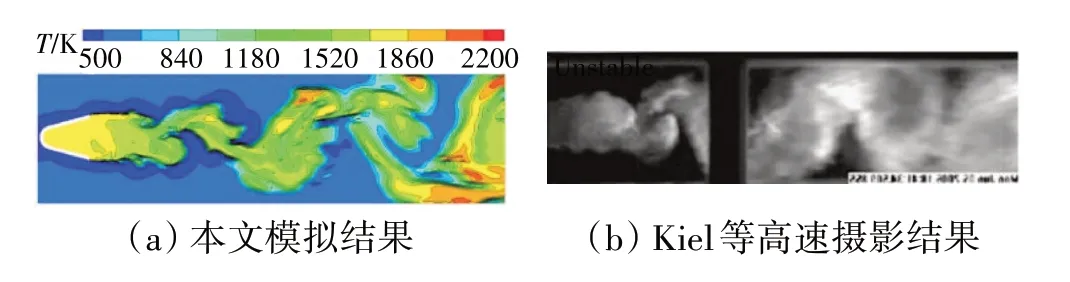
图7 钝体稳定器尾迹火焰形态

1.4 物性参数与边界条件

计算域中流体介质为空气或者航空煤油多组分混合物。介质的物性参数设置包括密度、定压比热容cp、动力粘度μ和导热系数λ。对于空气分别采用分段多项式（Piecewise-polynomial）、Sutherland 公式、动力学理论（Kinetic-theory）进行计算；对于混合物采用混合定律计算；对于密度项ρ均选择理想不可压缩气体。

边界条件：采用速度进口、压力出口，壁面采用固壁无滑移边界，展向2个表面采用平移周期边界。

2 稳定器后燃烧不稳定的影响因素

给出本文的基准参数，然后在此基础上对部分参数进行修改来研究钝体稳定器后燃烧不稳定的影响因素。

基准参数为：速度进口：Ma=0.1，900 K；压力出口：0.1 MPa；当量比：0.76。

在稳定器后中心截面沿流向方向设置5 个监测点用于分析燃烧室下游火焰的脉动情况。其流向坐标分别为：point-1（x=0.01 m）、point-2（x=0.05 m）、point-3（x=0.10 m）、point-4（x=0.20 m）、point-5（x=0.30 m）。监测点位置如图8所示。

图8 监测点位置

2.1 来流温度的影响

通常情况下，加力燃烧室的进口即是主燃烧室的出口，进入加力燃烧室的气体为经过主燃烧室燃烧并经过涡轮膨胀作功后的高温混气。相较于主燃烧室来说，加力燃烧室来流混气含氧量较低，燃烧条件相对较差，但从另一角度看，随着来流温度的升高，混气含氧量虽然降低，但温度提高对燃烧有利。选择3 种来流温度600、900、1200 K，分析来流温度变化对钝体稳定器后燃烧不稳定的影响。

通过简单的热力学分析[16]估算主燃烧室燃烧后的混气温度与混气成分之间的关系（假设燃油完全燃烧），计算得到的结果见表2。

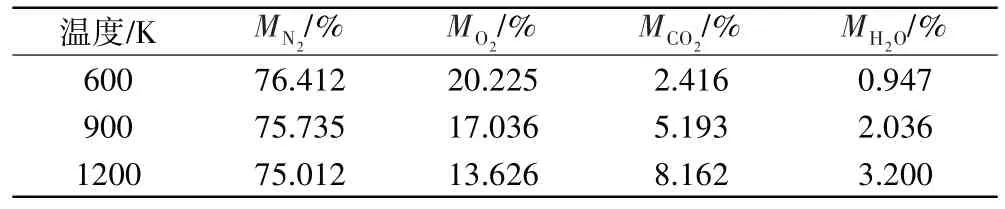
表2 不同温度时来流气体成分的质量分数

不同来流温度时钝体稳定器后温度分布如图9所示。从图中可见，不同来流温度对应钝体稳定器后火焰形态差异较大。当来流温度为600 K 时，稳定器后的火焰近似呈直线状，燃烧不稳定性主要体现在内部火焰与外部混气的交界处，整个交界处呈波浪形火焰，但此时火焰面还未出现大尺度旋涡，稳定器尾部火焰几乎完全呈现K-H 不稳定；当来流温度为900 K时，火焰形态由2 部分组成：稳定器尾缘向后延伸一小段长度的剪切层火焰，在剪切层火焰后原本的直线状火焰逐渐变为由BVK 不稳定主导的旋涡火焰；当来流气体温度达到1200 K 时，稳定器尾部火焰几乎完全呈现由BVK 不稳定主导的旋涡火焰，并且燃烧室下游火焰的摆动幅度很大。

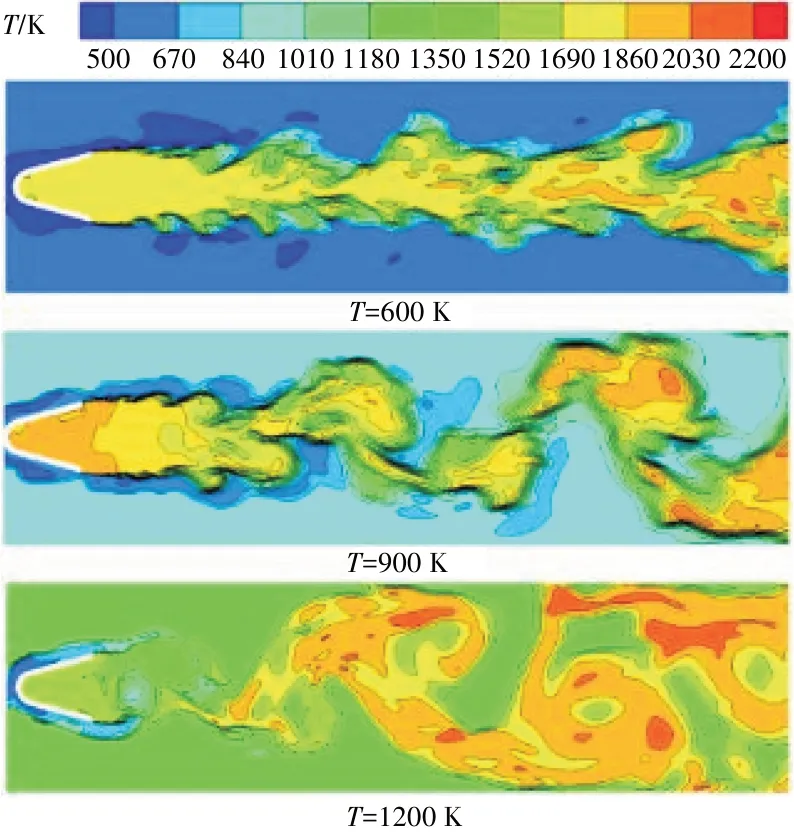
图9 不同来流温度时钝体稳定器后温度分布

通过上述分析可知，来流温度是影响稳定器后火焰形态的1 个重要因素。其深层原因之一是由于未气化的液态煤油不易改变方向，因此在来流温度较低时，低温油雾“包裹”在钝体稳定器后火焰表面抑制其向旋涡火焰转变；而当来流温度较高时，液态煤油会被高温来流气体加热而迅速气化，仅有少部分未来得及气化的低温油雾顺着稳定器两侧向下游流去，但很快就完全气化。因此在来流温度较高时，剪切层火焰向旋涡火焰转变的流向位置会提前。Gokulakrishnan等[17]同样以相似结构的钝体稳定器为研究对象，选择丙烷为燃料在来流温度为600 K 时稳定器后火焰形态与本文以液体煤油为燃料、来流温度为900 K 时的类似。

不同来流温度时钝体稳定器后速度分布如图10所示。从图中可见，稳定器后火焰由K-H 不稳定主导时，稳定器后流场速度分布分层较为明显。高速区主要集中在火焰与壁面之间，低速区主要集中在稳定器尾缘；而当火焰由K-H 不稳定向BVK 不稳定转变时，稳定器后非对称漩涡将极大影响流场中速度分布，从中心截面的瞬时速度分布可见，当BVK 不稳定出现后，在稳定器下游产生速度很高的涡团，使得原本相对规则的速度分布变得不均匀。

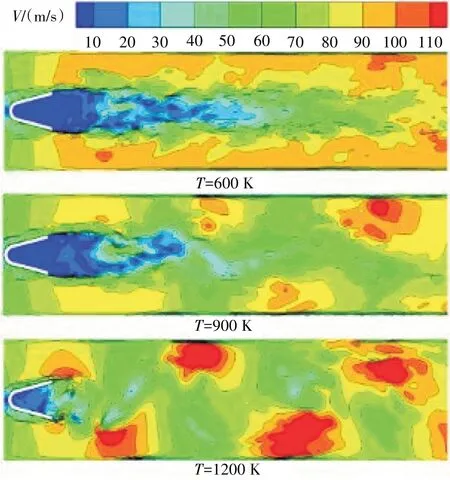
图10 不同来流温度时钝体稳定器后速度分布

2.2 来流马赫数的影响

来流马赫数通过影响湍流流动、油气混合、油气驻留时间等因素，进而影响钝体稳定器后火焰的燃烧不稳定现象。分别选取来流马赫数Ma=0.1、0.2、0.3，分析来流马赫数变化对稳定器后燃烧不稳定的影响。

不同来流马赫数时钝体稳定器后温度分布如图11 所示。从图中可见，从整体上看，3 种来流马赫数时稳定器后火焰形态非常接近，稳定器后几乎完全由BVK 不稳定主导的旋涡火焰占据，表明来流马赫数对稳定器后的火焰形态影响较小。但从细节上看，当来流马赫数较低时，稳定器后火焰面较为光滑，没有出现大量褶皱；而随着来流马赫数逐渐提高，火焰面逐渐凹凸不平，越来越多的褶皱出现在火焰表面。表明随着来流马赫数提高，稳定器后的火焰表面趋于破碎。由于燃油从雾化、蒸发需要一定时间，随着来流马赫数提高，低温燃油在燃烧室的驻留时间缩短。当马赫数为0.1 时，稳定器尾缘低温燃油（图中蓝色区域）基本消耗殆尽；而当来流马赫数提高到0.2 时，少量低温燃油出现在燃烧室中部；当来流马赫数达到0.3时，甚至在燃烧室下游也有低温燃油的存在。

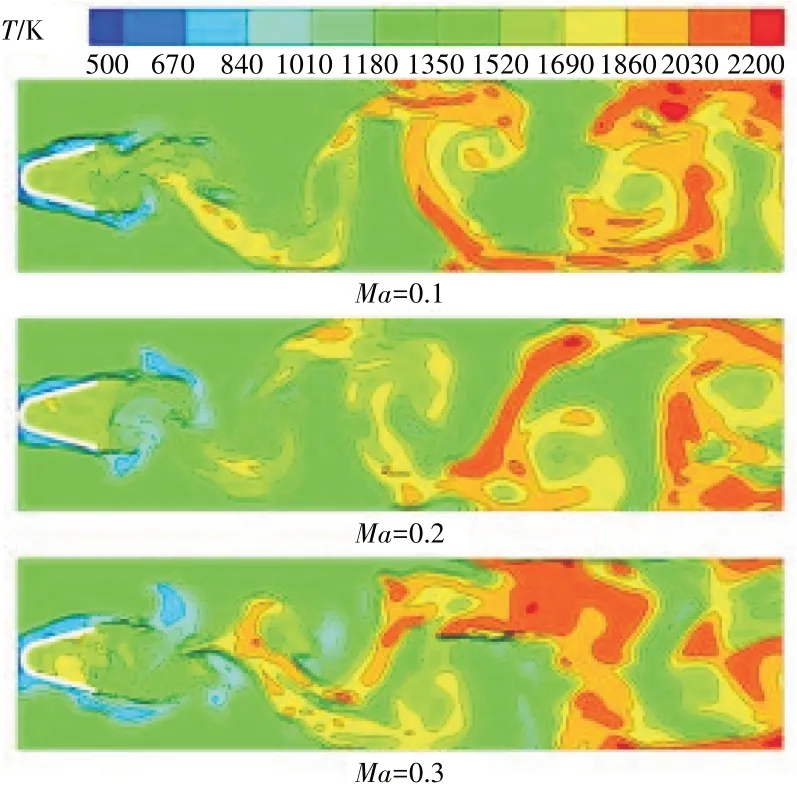
图11 不同来流马赫数时钝体稳定器后温度分布

由于来流马赫数不同，不能把三者的速度标尺设为一致。将3 种工况下速度标尺的上限设置为各自来流马赫数的2 倍，比较3 种来流马赫数时钝体稳定器后速度分布的变化。

不同来流马赫数时钝体稳定器后的速度分布如图12所示。从图中可见，从整体上看，三者的速度分布相似，这与温度分布的结果趋于一致。表明在由相同火焰不稳定性主导的区域具有相近的温度分布以及速度分布。但从细节上看，在低来流马赫数时，稳定器后方的涡团较为完整，尺寸较大且各涡团之间尺度相近；随着来流马赫数提高，稳定器后大尺度的涡团在高速气流的冲击下逐渐破碎成次级尺度涡团。

图12 不同来流马赫数时钝体稳定器后速度分布

为了分析钝体稳定器后火焰的脉动特征，设置监测点（图7）。以来流马赫数为0.3、监测点5 为例。将该点压力脉动与放热脉动的时域图和频域图进行整理，如图13所示。

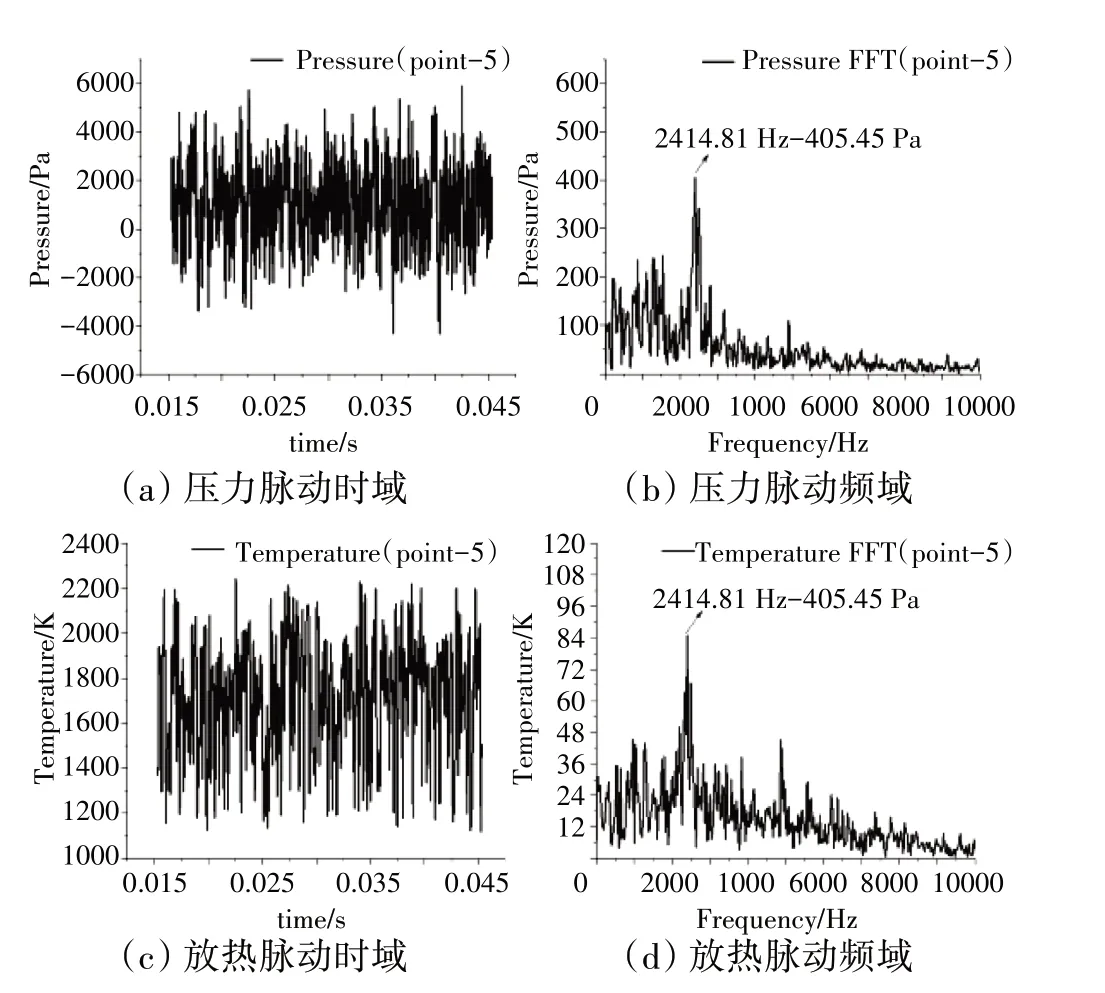
图13 监测点5压力脉动与放热脉动时域与频域

从图13（a）、（c）中可见，无论是压力脉动还是放热脉动，时域曲线均充满毛刺，表明流场中除了大尺度涡以外还存在小尺度涡。对应到图13（b）、（d）上可得，频域曲线除了主频外，还存在很多与主频振幅可比的次频。

将3 种工况下钝体稳定器后监测点的时域曲线进行FFT 变换得到火焰压力脉动和放热脉动的频谱信息，分别如图14、15所示。

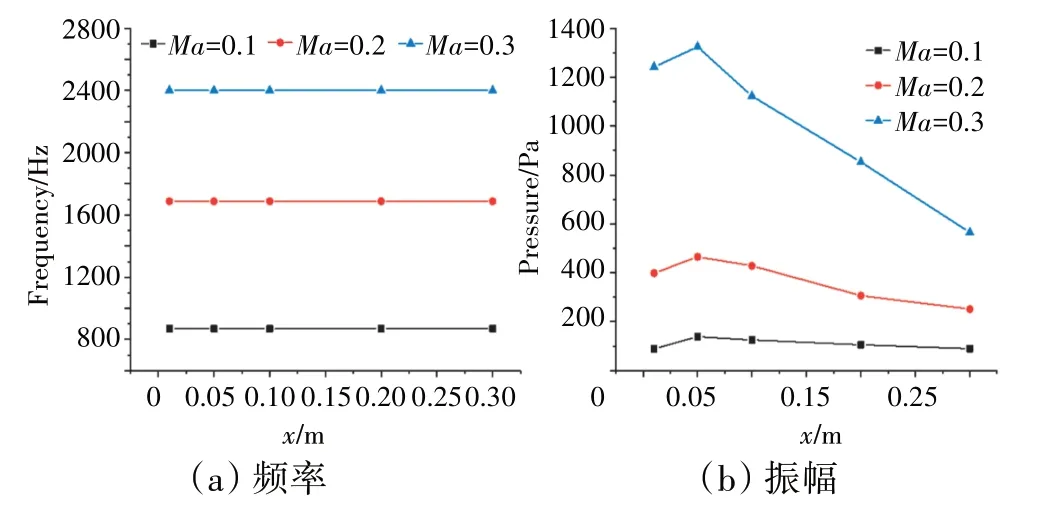
图14 不同来流马赫数时监测点压力脉动频域

从图14 中可见，随着来流马赫数提高，燃烧不稳定的压力脉动频率呈提高趋势。这是由于提升来流马赫数会加快稳定器尾缘非对称旋涡的生成，而这些非对称漩涡会对稳定器下游流场产生显著影响。压力脉动的振幅同样随着来流马赫数的提高而增大，这可以解释为提高来流马赫数会导致流场中各处的平均流速提高，进而导致气流压力脉动更剧烈。

对比图14（a）和图15（a）可见，发生燃烧不稳定现象时，火焰的放热脉动和压力脉动的频率较为接近，这是因为放热脉动和压力脉动均会受流场中大尺度旋涡的影响。从图15（b）中可见，一方面，当来流马赫数从0.1提高到0.2时，放热脉动的幅值呈增大趋势，这是因为适当提高来流马赫数使得稳定器下游油滴破碎程度更大，雾化效果更好。另一方面，当马赫数从0.2 提高到0.3 时，放热脉动幅值反而在3 种来流马赫数下最小。这可以解释为当来流马赫数过高时，尽管对稳定器后油雾破碎和混合有利，但同时减少了油气混合的时间和油雾在燃烧室的驻留时间，且过快的气流会将燃烧不稳定产生的热量过早带出燃烧室，不利于热量的累积。

图15 不同来流马赫数时监测点放热脉动频域

2.3 当量比的影响

钝体稳定器后的燃烧不稳定现象与当量比密切相关。选取当量比为0.5、0.6、0.7，分别当量比变化对稳定器后燃烧不稳定的影响。

不同当量比时钝体稳定器后温度分布如图16 所示。从图中可见，在不同当量比时钝体稳定器后火焰形态趋于一致，均为剪切层火焰和旋涡火焰共存，2种火焰形态的过渡位置在流向方向位置也几乎一致。表明当量比从0.5增大到0.7时，不会对稳定器尾部火焰形态造成显著影响。

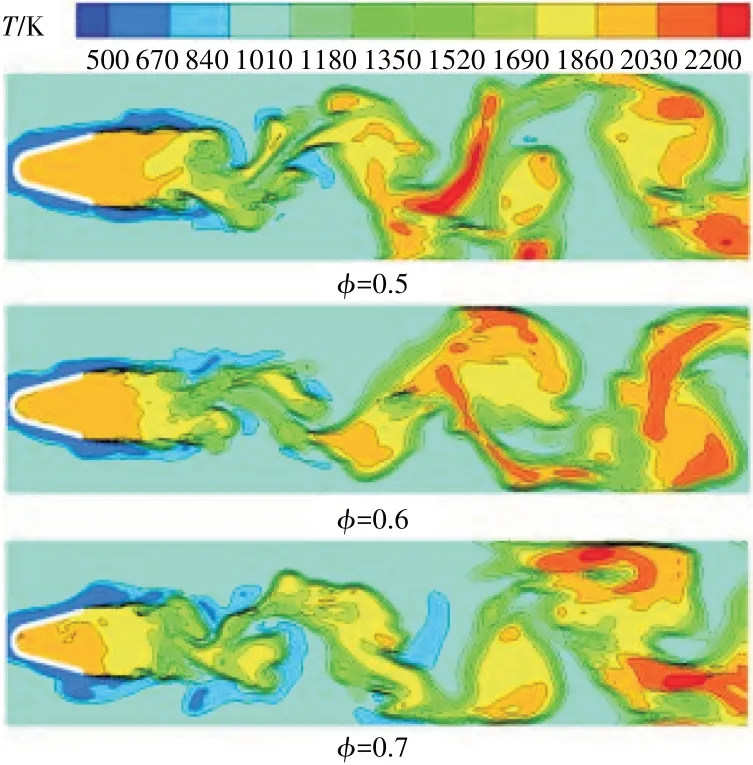
图16 不同当量比时钝体稳定器后温度分布

不同当量比时钝体稳定器后速度分布如图17 所示。从图中可见，从整体上看，3 种当量比时稳定器后速度分布基本一致，均在稳定器外侧形成速度梯度，在稳定器尾缘形成一定范围的低速区，且在低速区尾部出现K-H 不稳定与BVK 不稳定的过渡；但从细节来看，当量比为0.5 时Φ= 0.5，在BVK 主导的旋涡火焰区域出现尺寸较大的圆形或椭圆形的涡团；而当量比为0.6Φ= 0.6 时，这些涡团被拉伸，形状呈条状；随着当量比增大到为0.7Φ=0.7时，被拉伸的涡团破碎成更小尺度的涡团。表明随着当量比的增大，燃烧室下游的燃烧情况更为复杂，其中的火焰尺度更广。

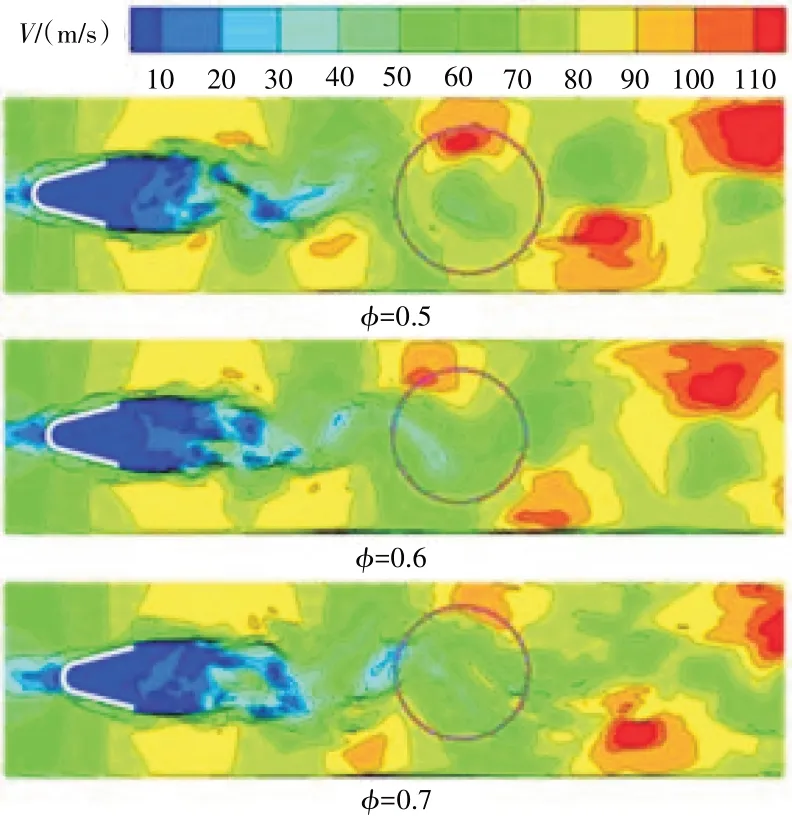
图17 不同当量比时钝体稳定器后速度分布

不同当量比时监测点压力脉动和放热脉动的频域如图18、19 所示。从图中可见，随着当量比从0.5增大到0.7，火焰的脉动频率变化较小，表明在一定范围内火焰的脉动频率对当量比并不敏感。随着当量比从0.5 增大到0.6，压力脉动的幅值对应增大，而当量比从0.6 增大到0.7，压力脉动幅值却不增反减；放热脉动的幅值变化趋势与之基本相同。这可以解释为稳定器后存在1 个局部最佳当量比，在当量比小于局部最佳当量比时，增大供油量会加快化学反应速率，提高燃烧室内平均温度；而当量比大于局部最佳当量比时，再增大供油量将会使稳定器后局部富油，过量的低温油雾不仅会抑制火焰燃烧而且使得燃烧室下游平均温度降低。

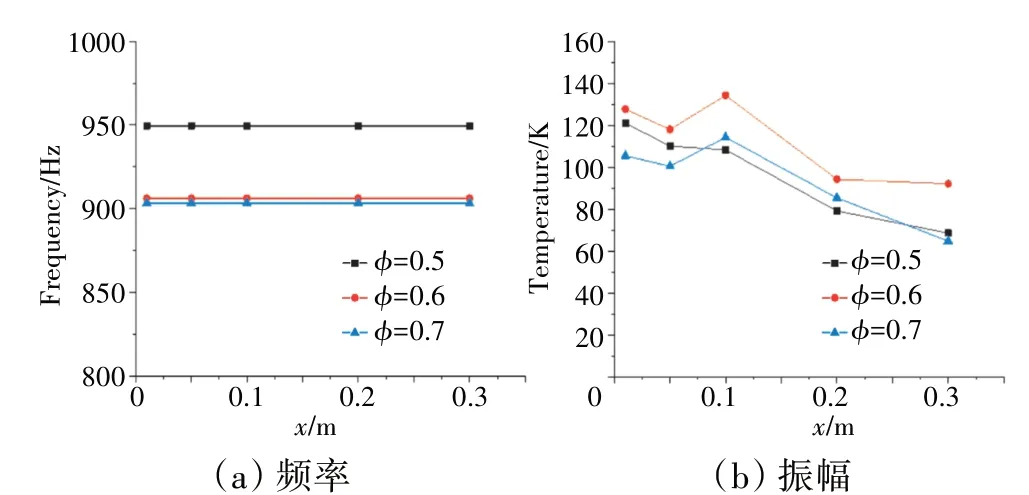
图18 不同当量比时监测点压力脉动频域

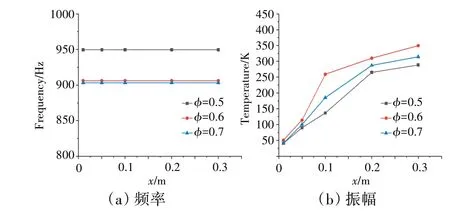
图19 不同当量比时监测点放热脉动频域

本文选择的FR/ED 模型只能用于单步或双步反应，对于湍流燃烧的细节刻画较为粗糙。根据Porumbel 等[18]的观点：FR/ED 模型容易高估反应区的厚度，采用该模型计算得到剪切层火焰的长度与厚度可能偏高，这可能是导致当量比改变时稳定器后火焰形态变化较小的一种原因。但同时Porumbel也指出，在稳定器下游由于燃烧过程化学能的添加使FR/ED 模型在远离稳定器的区域的预测能力有所提升。

3 结论

（1）来流温度对稳定器后火焰形态有显著影响。当来流温度为600 K 时，稳定器后火焰形态由K-H 不稳定主导；而当来流温度升到高900 K 时，K-H 不稳定与BVK 不稳定共存；当来流温度达到1200 K 时，稳定器后火焰形态由BVK不稳定主导。

（2）来流马赫数对稳定器后火焰形态影响较小；提升来流马赫数会显著提高火焰的脉动频率，并且压力脉动的幅值也有同样的变化趋势。但提升来流马赫数会对燃烧产生2 种相反的影响：一方面，提高来流马赫数会使得燃油破碎更好，油雾混合更充分，有利于燃烧；另一方面过高的来流马赫数使得油雾的驻留时间缩短，并且将燃烧产生的热量迅速带走，对火焰的放热脉动产生不利影响。

（3）燃油当量比从0.5增大到0.7时稳定器后火焰形态变化较小。稳定器后存在局部最佳当量比。当超过局部最佳当量比时继续增大供油量，局部富油会抑制火焰的放热脉动。