航空燃气涡轮发动机碰摩研究现状与展望

于平超 ，陶玄君 ，刘中华 ，曾振坤 ，蒋紫菡 ，张大义 ，4

（1.南京航空航天大学民航学院，南京 211106；2.空军装备部驻沈阳地区第二军事代表室，沈阳 110043；3.北京航空航天大学能源与动力工程学院，4.航空发动机结构强度北京市重点实验室：北京 100191）

0 引言

航空燃气涡轮发动机（简称发动机）是军用歼击机、大型运输机等飞行器的首选动力装置，也是中国“十四五”规划和2035 年远景目标的重要关注对象，作为高精尖装备的代表，其发展水平是一个国家科技水平和工业实力的综合体现[1]。由于发动机对气动效率的极高要求，转-静件间隙不断减小，甚至达到巡航状态下的零间隙设计；而发动机转速工况多变、受力状态复杂（除承受常规不平衡激励和热载荷外，还承受飞行器加速/转弯等带来的陀螺力矩等惯性过载、飞行器着陆时的基础冲击、砂石/飞鸟等外物被吸入时的轴向冲击、叶片丢失产生的径向冲击等），在工作过程中不可避免地出现转静件间隙变化。因此，碰摩一直是航空发动机中的常见现象，也是影响其结构可靠性与安全性的关键问题之一。

虽然碰摩通常属于后继故障，但一旦发生，不仅会造成碰摩件局部损伤，还能诱发转子甚至整机系统的复杂振动和失稳破坏，极大地危及飞行安全。国内外发动机相关指南规范对碰摩问题均有直接或间接的说明和要求。针对常规工况，GJB214A[2]、JSSG-2007B[3]规定：发动机在工作包线内工作时，叶片与轮盘不得与除封严件及外环以外的任何发动机静止构件接触；在规定的陀螺力矩作用下，叶片不能出现过度磨损和损伤。针对叶片丢失、吞鸟等恶劣工况，中国民用航空局（Ciril Aviation Administration of China，CAAC）和美国联邦航空管理局（Federal Aeronantics Administration，FAA）的咨询通告[4-6]均规定：发动机发生叶片丢失或不同程度的吞鸟后，应具备在规定功率下持续运转一段时间或成功停车的能力，且机匣和转子不能发生严重破坏。在过去半个多世纪，学者们围绕碰摩问题开展了大量研究，对相关理论进展进行了系统总结，例如：Muszynska[7]综述了1989 年之前，在转静碰摩建模和转子响应机理等方面的研究工作；江俊等[8]从动力学与控制角度对理论研究中的碰摩局部模型和系统模型进行了归类，并总结了碰摩非线性响应方面的研究成果；Ma 等[9-10]对叶片-机匣碰摩动力学研究进行了回顾，重点介绍了机匣涂层建模、磨损行为及对整体振动特性的影响。

总的来说，当前针对转静件碰摩问题的研究文献数量庞大，研究角度广泛，侧重点也不尽相同，然而已有综述论文多从非线性动力学角度总结理论方面的进展和突破，至今尚未有专门针对航空发动机碰摩问题的综述。相比地面旋转机械，发动机整体刚度更弱，承受负荷更高，部件形式更为多样，加之对结构可靠性/安全性的特殊要求，其在碰摩作用下存在着诸多特殊力学行为和亟需关注的工程问题。

本文聚焦于发动机这类高速复杂旋转机械，对相关的碰摩动力学建模和非线性动力学特性进行综述，并结合发动机特点给出未来针对发动机碰摩研究的展望，以期为发动机碰摩问题的研究提供参考。

1 发动机碰摩类型与物理效应

1.1 发动机碰摩类型

高涵道比涡扇发动机结构及典型部位的碰摩如图1 所示。从图中可见，转静子整体极为紧凑，结构部件繁多，各部件特征差异大，在服役期内会出现多种多样的碰摩：（1）不同部位的碰摩，如叶片-机匣、篦齿密封组件、静叶-旋转鼓筒、高-低压转子轴间的碰摩等.（2）不同方式的碰摩，如轴向和径向的碰摩。其中，转子系统径向碰摩、叶片-机匣径向碰摩是航空发动机中最关注的2 类碰摩故障。本文中提及的碰摩如无特殊说明均指径向碰摩。

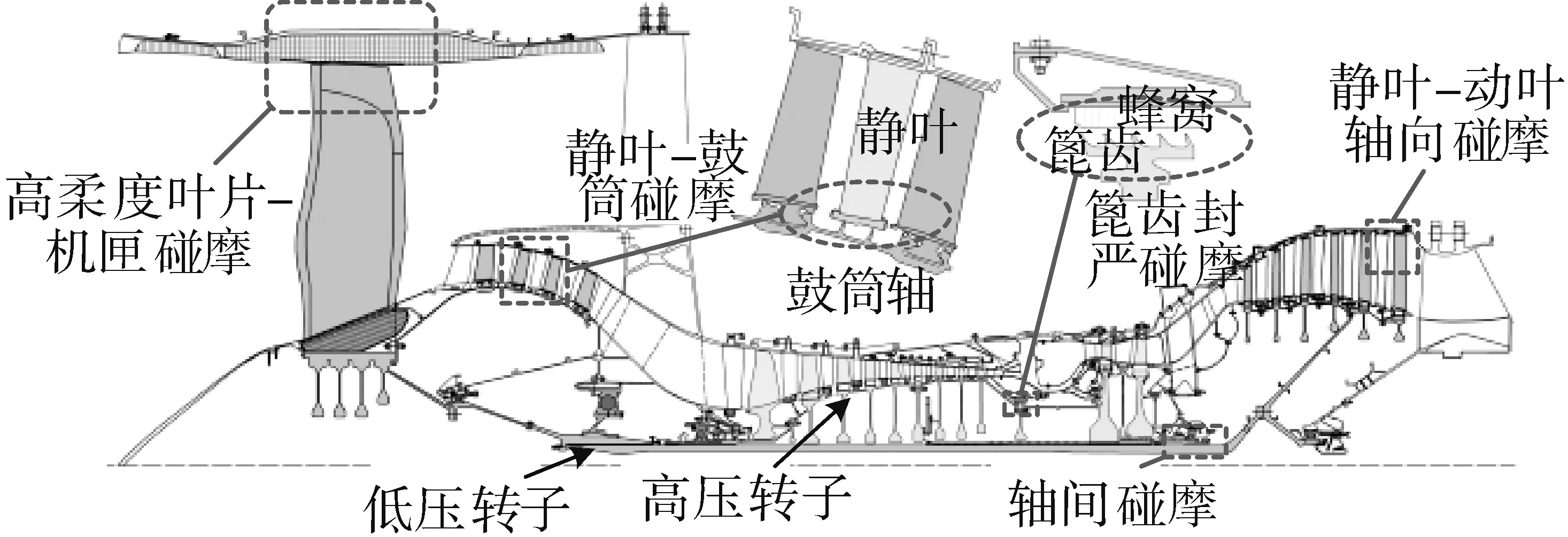
图1 高涵道比涡扇发动机结构及典型部位的碰摩

由于不同部位的结构件力学特性差异较大，即使是同类碰摩，若发生位置不同，转静件的力学行为和系统响应特征也会表现出显著差异。根据碰摩现象和转子运动特征，可大体将发动机中的转静碰摩分为全周碰摩、干摩擦反向涡动和间歇碰摩3类。

（1）全周碰摩。该类型碰摩发生时，转子在运动过程中一直与静子保持接触，其涡动方向与转子自转方向一致。全周碰摩是一种以不平衡激励为主导的碰摩形式，碰摩响应中以转频为主，理想情况下转子进动频率等于自转频率，称为同步全周碰摩。通常，全周碰摩时转子振幅相对较小，属于轻度碰摩。该过程中，静子对转子施加稳定的径向-切向载荷，类似于附加支承，导致振幅和相位变化。相比无碰摩转子，其响应波峰更为平坦，同步响应相位滞后较小，峰值转速（即共振转速）更高。

这种碰摩状态多发生于发动机新结构的初期试验状态。例如，为保证气动效率，发动机在静子部位采用材质较软的涂层材料，并使关键部位的转静间隙为负，这样通过几次磨合试车，使转静子主动发生全周剐蹭碰摩，从而达到较满意的径向配合。

（2）干摩擦反向涡动（简称反向涡动）。这是一类破坏性极强的碰摩形式，转子在碰摩过程中一直与静子保持接触，涡动方向与转子自转方向相反。这类碰摩与全周碰摩有本质不同，从力学上其为一类自激振动，能量来源并非不平衡激振力，而是接触面摩擦力将转子旋转的一部分能量转化为转子横向振动的能量，反向涡动的主导因素是碰摩点处切向摩擦力。相关试验表明：反向涡动可以通过在很低的转速下对转轴扰动而被诱发，也可以在超过某一临界转速由不平衡量激励而诱发；反向涡动发生时转子反进动频率值与不平衡激振频率无关，通常等于碰摩系统的非线性模态频率。

在反向涡动状态下，转子振幅极大，且由于转子涡动频率与自转频率不相同，轴系内将会产生高幅值交变应力，能导致转子迅速破坏，是发动机中必须避免的一种碰摩形式。实际中，当发生叶片丢失时，转静件在大不平衡载荷下能发生严重碰摩，接触点处摩擦力极大，容易诱发干摩擦反向涡动。

（3）间歇碰摩。指转子与静子碰撞后，在一段区域内保持接触摩擦作用，随后相互脱离，并以较高频率、长时间的重复上述过程，表现出持续的“碰撞-摩擦-反弹-分离”的物理特征。间歇碰摩是一种由于不平衡力、碰摩径向力和切向摩擦力共同主导的碰摩形式，不平衡力引起转子的横向弯曲并使其涡动，碰摩径向力和切向摩擦力则改变转子进动速度和进动形式，一方面间歇碰摩时径向冲击可能使转子产生瞬时横向振动和扭转振动，并引起转子的反弹运动，另一方面切向的摩擦作用可能改变转子反弹运动的轨道甚至引起转子的瞬时反向运动，碰摩径向力和切向力产生的振动响应与不平衡激励产生的响应叠加，最终形成了一种复杂的、重复性的且总体较为稳定的碰摩运动形式。因此，在间歇碰摩状态下，在转子频域响应中通常能观察到丰富的频域成分，包括分频、倍频及各类组合频率成分等。

间歇碰摩可引起转子系统刚度的轻微改变，并使系统刚度具有周期时变特征，刚度的时变特征可能引起转子系统不稳定，并诱导出转子的自激振动失稳。

1.2 碰摩力学效应及引起的转子损伤失效

从动力学角度看，碰摩主要产生3 种力学效应：（1）冲击效应。主要是转静件碰撞接触瞬时的径向-切向冲击力，是典型的瞬态过程，频域中具有宽频特征，能激起转子瞬态横向振动和部分扭转振动，并与旋转运动、受迫进动叠加形成转子复杂振动响应。（2）摩擦效应。由转静件接触点处的相对滑动产生，一方面能引起局部热膨胀导致转子发生热弯曲，进而造成转子振幅-相位甚至进动速度的改变；另一方面，切向摩擦载荷本身显著影响转子进动速度，当发生严重剐蹭性碰摩时，较大摩擦力甚至能导致转子发生反向涡动；此外，摩擦本身具有非线性特征，导致转子高次谐波等频率成分的产生，其形成的附加扭矩还将引起转子复杂扭转振动。（3）附加约束或耦合效应。当转静件碰摩接触时，转子和静子在力学上成为1 个动力学耦合系统，导致转子及整机振动模态的变化甚至形成新的耦合振动模态。若仅关注转子，碰摩则体现为一种附加约束（类似于附加支点），导致转子刚度增大，改变转子模态频率和振型。随着发动机转静子系统刚度不断降低，这种耦合效应或附加约束影响愈发显著，在动力学分析中要尤其关注。另外，由于转静子接触状态随时间发生改变，这种耦合或约束具有时变特征，其对转-静子模态特性的影响远比线性系统复杂。

在严重碰摩状态下，转子系统可能发生多种失效形式，碰摩动力学影响及导致的转子失效模式如图2所示。基于上述力学效应和响应特征，可归结为3类：（1）卡滞扭转断裂破坏，转静件持续摩擦时，接触表面将产生较高温度而发生局部熔化，造成转子卡死，这种情况下转子承受巨大扭转力矩，使转子发生扭转断裂。（2）反向涡动失稳破坏，主要由接触点处切向摩擦载荷引起，在碰摩过程中摩擦力不断把旋转能量转移到转子横向振动中，当其超过转子系统阻尼的平衡能力时，转子会发生反向涡动失稳，轴系内产生高频高幅交变应力，使转子轴系短时间内疲劳破坏。（3）弯扭耦合振动失稳破坏，发动机低压转子两端质量-转动惯量大，轴间轴段细长，弯曲和扭转刚度低，碰摩切向冲击导致转子极易发生扭转振动，并在某些情况下与弯曲振动发生强烈耦合，甚至产生失稳，轴系内产生高幅交变剪切应力，最终发生扭转断裂。

图2 碰摩动力学影响及导致的转子失效模式

2 航空发动机碰摩动力学建模研究现状

为定量分析碰摩对发动机转静子系统动力学特性的影响，首要前提是建立能充分反映碰摩过程的力学模型，涉及到描述碰摩接触过程的局部碰摩力学模型和计及碰摩作用的结构整体力学模型。

2.1 局部碰摩力学模型

局部碰摩力学模型用于刻画转子与静子开始接触-相互作用-彼此分离的碰摩过程。目前，国内外学者广泛采用切向力函数和法向力函数描述该碰摩过程，其中对于切向力的描述，库伦摩擦模型能够取得较好模拟效果在碰摩分析中最常采用，而对于法向力的描述，国内外学者则提出了多种描述模型。依据发动机部件结构特征的不同，下面将分为封严-转子轴间碰摩和叶片-机匣碰摩2类结构件的法向碰摩力模型予以综述。

2.1.1 封严或轴间碰摩

对于航空发动机高-低压转子轴间或转动篦齿与静子件之间的碰摩，通常将其简化为2 个理想圆柱体的碰摩，如图3所示。在各类模型中，最常采用线弹性模型[11-13]

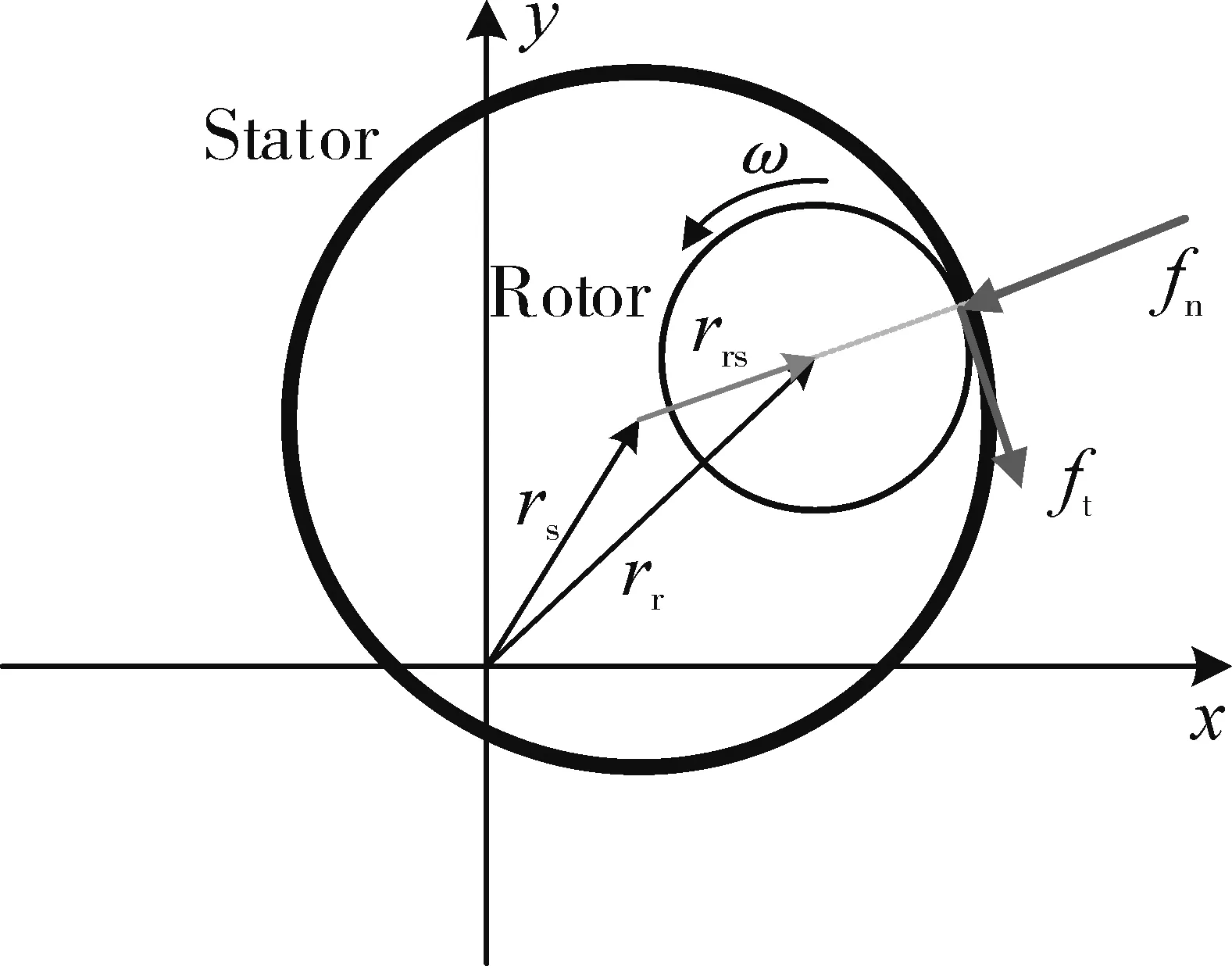
图3 柱面-柱面碰摩

式中：δ为相对侵入位移；ks为碰摩刚度，基于经验取值或者近似为静子刚度。

进一步考虑碰摩过程中的能量损失，Hunt等[14]在线弹性模型基础上引入阻尼项模拟能量耗散，提出了改进线弹性力学（Kelvin-Voigt）模型

式中：c为法向黏性阻尼系数。

引入阻尼项可以考虑碰摩过程中的机械能和热能损失，但转子与静子恰好接触时，碰摩力可能小于0，这与实际不符。

线弹性模型隐含转静碰摩过程中接触刚度为定值这一假设，但对弹性接触的研究表明，2 个相对滑动的接触物体之间的法向力与位移关系是非线性的。借助于Hertz 接触理论，袁惠群[15]、杨树华等[16]建立了2 个圆柱面接触的非线性法向碰摩力模型；Lankarani等[17]基于上述模型引入阻尼项提出了更为完善的法向碰摩力（Lankarani-Nikravesh）模型

式中：kh为刚度系数，根据碰摩件材料参数和结构参数获得；ch为阻尼系数，取决于刚度系数、初始碰撞速度及碰摩前后速度恢复系数；指数n取为1.5。

上述模型假设2 个圆柱体接触时为点接触，且接触面是光滑的。Varney 等[18]认为碰摩件接触表面由不同高度微凸体组成，具有一定粗糙度，在接触过程中不同微凸体存在着弹塑性变形，为此基于弹塑性理论和接触面统计学模型建立了考虑2 个圆柱接触面粗糙度的法向碰摩力模型，并将其与线弹性模型进行了对比，如图4所示。

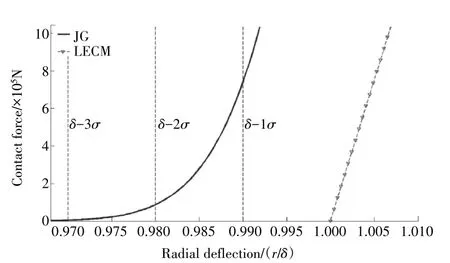
图4 考虑粗糙度的碰摩模型（JG）与线弹性碰摩模型（LECM）的对比

然而，发动机篦齿封严碰摩远比2 个光滑圆柱体接触复杂，篦齿形状、多道篦齿影响、蜂窝或其它软质涂层的使用，导致碰摩接触力随侵入深度呈现更为复杂的非线性关系。近年来，Fischer 等[19-20]、Xuan等[21-22]仿真和试验研究了发动机中篦齿结构-蜂窝涂层机匣的碰摩力学过程，重点关注了封严件磨损情况、碰摩力及接触面温度变化情况，如图5 所示。不过，目前还没有学者综合考虑篦齿-涂层磨损、热效应及部件局部变形，建立能更真实反映发动机这类特定篦齿-蜂窝（或其它涂层）机匣碰摩过程的碰摩力模型。

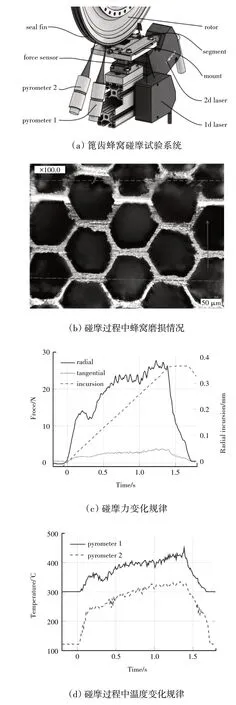
图5 篦齿-蜂窝机匣碰摩过程中碰摩力及蜂窝磨损与温度变化

2.1.2 叶片-机匣碰摩

对于叶片-机匣碰摩，根据建模时是否考虑机匣内壁涂层可分为叶片-裸机匣碰摩和叶片-涂层机匣碰摩2大类。

2.1.2.1 叶片-裸机匣碰摩

在叶片-裸机匣碰摩建模中，主要考虑碰摩过程中叶片-机匣变形对碰摩力的影响。基于准静态变形假设和能量守恒，Padovan 等[23]建立了弹性叶片-刚性机匣碰摩模型；采用相似思路，Jiang 等[24]考虑叶片旋转刚化效应对模型进行了扩展；Ma 等[25]进一步将机匣静变形效应考虑在内，提出了弹性叶片-弹性机匣碰摩模型，其法向力为

式中：kc为机匣平均刚度；L为叶片长度；α=（Rd+L）/L；Rd为轮盘半径；δ为叶尖与机匣在碰摩点处的相对位移；μ为叶片材料泊松比；Γ1=Γ0/kc，Γ0与叶片参数和转子旋转速度相关。

然而，碰摩本质上是高度非线性的动态过程，随着叶片-机匣柔度越来越高，在碰摩过程中叶片、机匣发生显著振动变形并与碰摩力相互耦合影响，前述准静态变形假设不再适用。为此，一些学者利用有限元等方法离散叶片和机匣，采用线性或非线性形式的碰摩力模型，如式（4）或接触动力学方法模拟叶尖-机匣碰摩接触，并通过显式、隐式等数值方法求解该非线性接触动力学问题，进而获得叶片-机匣动态碰摩力及部件振动变形。Thiery 等[12]、Sinha[26]、Parent等[27]在研究转子碰摩响应时，对叶片与机匣之间的碰摩采用了线弹性模型；Legrand 等[28]采用拉格朗日乘子法处理碰摩接触问题，建立了叶片和机匣的2 维模型，研究了碰摩导致的模态耦合现象；Batailly 等[29]分别叶片和机匣采用直梁和曲梁建模，同样基于拉格朗日乘子法研究了叶尖和机匣的碰摩问题；Zeng 等[30-31]采用梁-壳-弹簧混合单元建立叶盘和机匣模型（如图6 所示），并采用中心差分法联合拉格朗日乘子法求解叶尖-机匣碰摩接触；刘书国等[32]、柴象海等[33]开发了叶片-机匣碰摩的显示动力学模拟技术，对叶片与机匣之间的碰摩作用采用罚函数法模拟，能够高保真的反映叶片和机匣的杂结构特征。

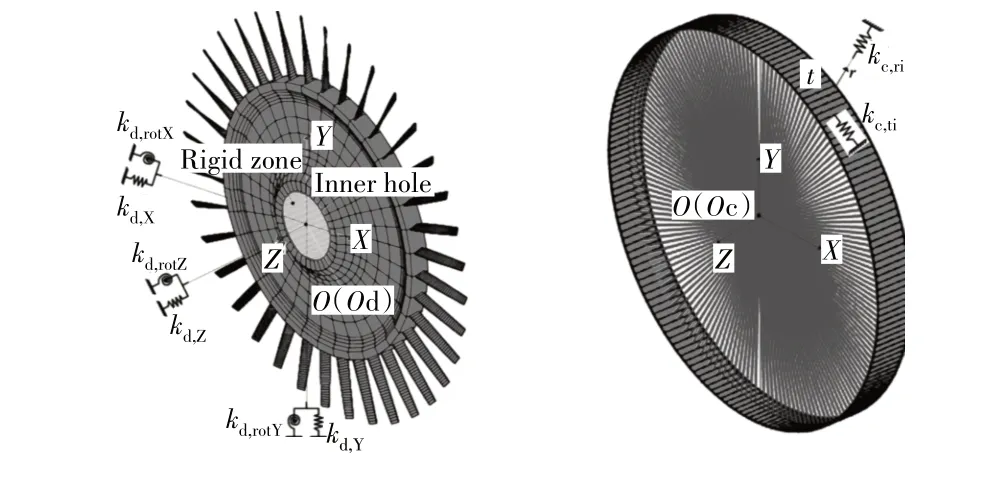
图6 基于梁-壳-弹簧混合单元的叶片-机匣碰摩动力学模型[31]

2.1.2.2 叶片-涂层机匣碰摩

在叶片-涂层机匣碰摩建模中，关键是在已有叶片-裸机匣碰摩模型基础上考虑涂层影响。张俊红等[34]建立了叶片-涂层机匣碰摩的显示动力学模型，涂层建模采用与机匣相似的实体单元，通过赋予涂层不同的弹性模量来反映涂层对碰摩力的影响；Cao等[35]将柔性叶片和机匣分别简化为线性弹簧，通过Hertz 接触理论、能量守恒、动量守恒定律推导得到了碰摩时涂层局部刚度及能量损失，进而提出了新型迟滞碰摩力模型

式中：kc、kb、kh分别为机匣刚度、叶片刚度和Hertz 接触刚度；e为碰撞恢复系数；δ为包含叶片-机匣整体变形和涂层局部变形的总侵入变形；δ̇-为初始侵入速度；δh为涂层局部变形。

然而，在发动机中为避免叶片与机匣接触时的损伤，机匣内壁的涂层通常是材质较软的可磨损涂层，因此叶片与机匣碰摩时涂层存在显著的磨损。在此方面，国内外学者也提出了多种可考虑涂层磨损的叶片-机匣碰摩力学模型，典型的包括基于线性磨损准则碰摩模型、基于Archard 磨损准则的碰摩模型以及基于塑性本构关系的碰摩模型，其中基于塑性本构关系的叶片-涂层机匣碰摩模型在发动机碰摩分析中得到了较多应用。Legrand 等[36-38]提出了利用双线性弹塑性杆单元模拟可磨损涂层，基于杆单元的涂层磨损模型如图7 所示。模型中利用弹性模量、塑性模量及屈服极限3 个重要参数处理磨损，并通过时域数值积分方法获得每个时间步下的磨损轮廓。在上述涂层磨损分析方法之上，陈大玮等[39]建立了计及复杂几何造型的宽弦风扇叶片与涂层机匣碰摩的动力学模型，实现了结构振动及涂层磨损的定量分析和评估。

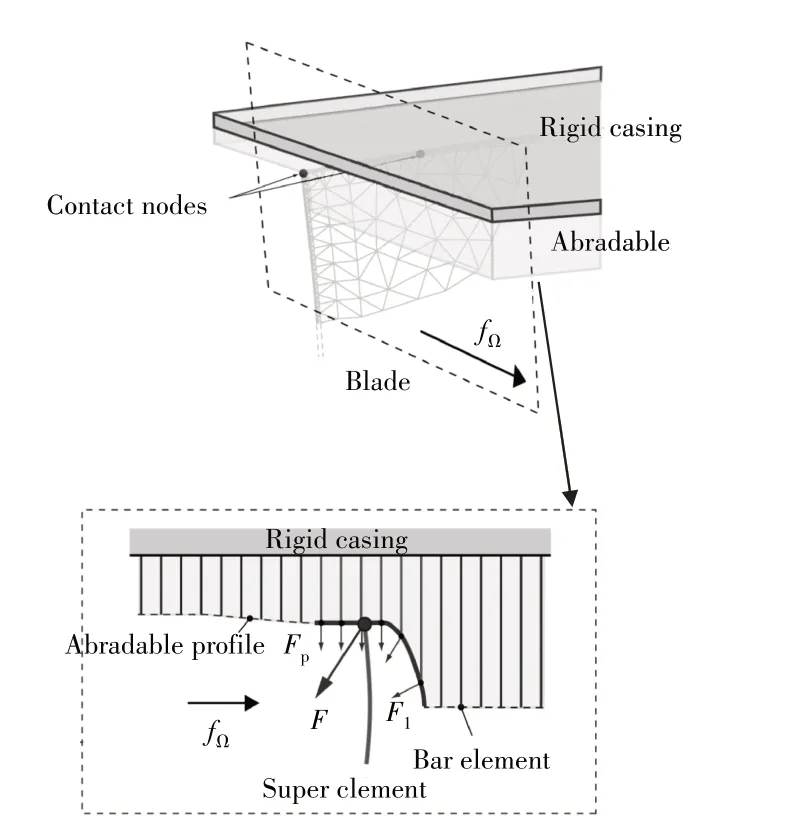
图7 基于杆单元的涂层磨损模型

总的来说，目前已经提出了多种用于叶片-机匣碰摩过程描述的局部力学模型，这些模型基于各自的简化和假设，适用条件不尽相同且各有优缺，例如基于准静态变形假设的叶片-机匣碰摩模型能够显式反映碰摩力与结构参数和工作参数之间的关系，可方便的植入转子甚至整机碰摩仿真分析中，但模型所基于的假设使其不能准确模拟高速碰撞时的碰摩力变化规律；基于接触动力学的方法虽然能够更好的分析高速碰撞过程，但计算时要处理叶片-机匣振动变形、复杂接触判断及数值迭代，计算效率低、难以收敛，应用该方法进行整机碰摩动力学分析时将显得更为困难。

2.2 结构碰摩的整体力学模型

碰摩整体动力学建模的关键在于可以较精确地模拟转静件结构特征，并合理地描述碰摩形式（间隙碰摩、全周碰摩等）。前者涉及的是转子、静子乃至整机的动力学建模问题，常用的包括解析法、传递矩阵法和有限元法，其中有限元由于其精度高、适用性强等优势已成为目前发动机动力学建模的主流方法。邓四二等[40]、陈果[41]、Pham 等[42-44]基于梁单元法建立了双转子及3 转子航空发动机的整机耦合动力学模型。梁单元法优点是模型规模小，便于开展非线性振动分析，但需要事先对结构进行仔细简化和划分来保证力学特征的等效。近年来，部分学者开始应用2 维或3维实体有限元建模，陈萌、张力等[45-46]提出了发动机中转子、静子及整机系统的3 维有限元建模方法，并对建模方法的精度进行了分析；孙传宗等[47]、于平超等[48]在双转子碰摩动力学分析中亦采用了实体单元对转子进行了建模。

在碰摩整体动力学建模中，对于碰摩形式的模拟大致包含2 种思路。第1 种是基于前述线弹性模型、叶片-机匣模型等局部模型，这类局部模型能够显式表达碰摩力与转静件结构参数、侵入位移的关系，在研究转子动力学特性时只需将碰摩力施加到转子对应节点上。对于不同的碰摩形式，通过定义接触函数判断碰摩是否发生并模拟碰摩力，例如：Han 等[49]在研究转子单点碰摩时，Abuzaid 等[50]在研究局部碰摩时，均采用周期阶跃函数，如图8 所示，用以模拟在特定区域内的碰摩。

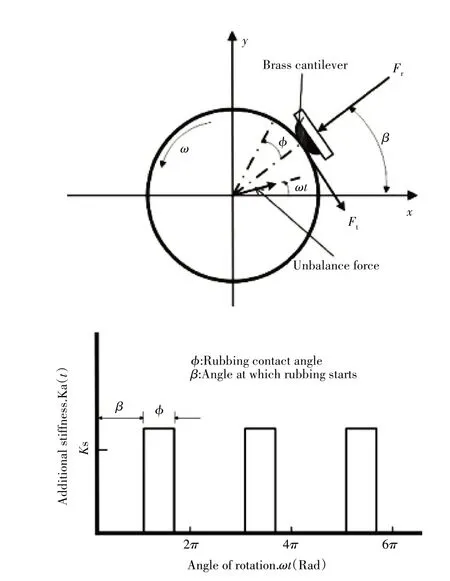
图8 局部碰摩及其周期阶跃函数

第2 种为基于接触动力学的建模方法，该方法直接通过梁或实体单元等方法建立转静件整体有限元模型，然后在可能发生接触的位置定义接触单元，接触单元处理接触碰摩的算法包括罚函数法、拉格朗日乘子法及增广拉格朗日乘子法，在计算过程中通过合适的搜索方法判断和识别发生接触的位置。该方法模拟不同形式的碰摩是通过精确建立转静子模型来实现的，例如，Ma等[51-52]在多点碰摩分析中，将静子简化为空间均布的固定梁单元，转子盘采用质量单元模拟，并在可能出现碰摩的节点对设置点-点接触单元，如图9所示。

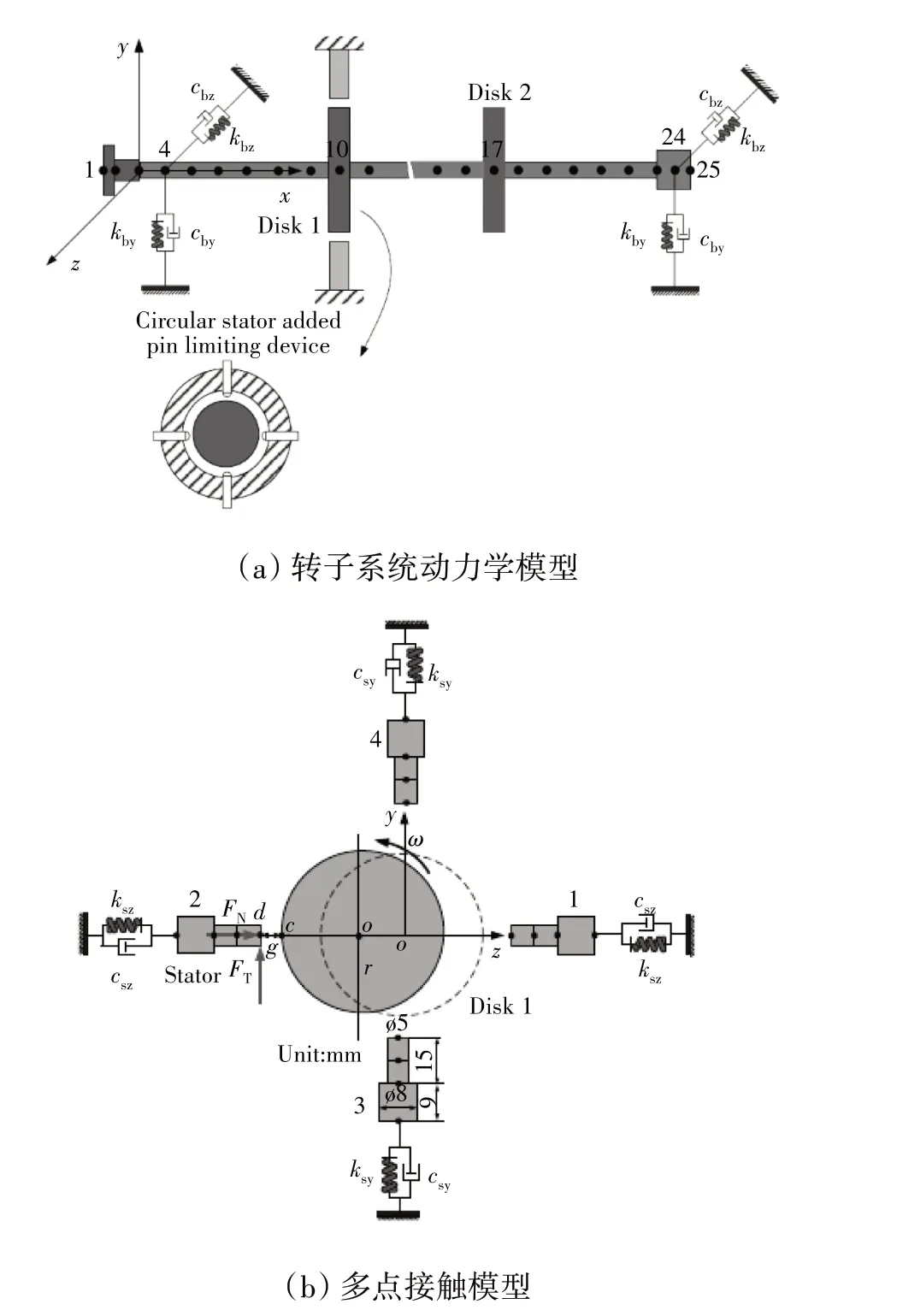
图9 转子系统多点碰摩动力学模型

3 碰摩非线性动力学特性研究

在以往碰摩动力学分析中，大多关注转子横向振动响应特征。随着发动机结构负荷的提高和各部件及整体结构刚度的减弱，参与碰摩的结构件、碰摩的形式及产生的动力学影响也更加多样，这极大促进了对碰摩动力学问题的研究和相关理论的发展。根据发动机研制使用过程中的工程问题和工程需求，从碰摩的横向振动、弯扭耦合振动、叶片-机匣振动、旋转壳体振动几方面进行综述。

3.1 转子碰摩的横向振动响应

转静子碰摩是一类非光滑的、高维强非线性系统，系统响应受多种参数控制且各参数互相影响，导致极为复杂的动力学现象，在此方面的研究涉及范围极广，包括碰摩转子动力学行为及随系统参数的演变和分岔规律、典型碰摩响应的产生机理和存在边界、附加约束下转子模态特性及与响应特性之间的关联等方面。

在碰摩转子动力学行为方面，Beatty[53]首次建立基于线性碰摩力模型研究了碰摩的典型故障特征；在Beatty的开创性工作基础上，Choy和Padovan等[54-55]对转子叶片-封严-机匣碰摩系统进行动力学建模，详细讨论了机匣刚度、摩擦系数等对系统响应的影响规律；Ehrich[56-57]、Chu 等[58-59]对碰摩转子的亚谐波/超谐波响应、周期/拟周期运动、混沌响应及系统各动力响应随参数变化的分岔规律进行了系统研究。上述工作基于简单转子，近年来围绕发动机转子这类特定工程对象也开展了大量研究，Wang 等[60]、Sun 等[47,61]、Yang 等[62]、Prabith 等[63]针对发动机双转子系统，研究了点碰摩、全周碰摩等不同碰摩形式下双转子稳态幅值变化、时频响应和稳定性特征。考虑机匣影响，Parent 等[27]、Chen 等[13,64-65]、Fei 等[66]、Jin 等[67]、Kang 等[68]建立了转子-支承-机匣碰摩耦合模型，详细讨论了碰摩作用下机匣加速度响应、转子轨迹特征、碰摩形式及响应分岔规律。

在典型碰摩响应产生机理及存在边界方面，包含同频全周碰摩、拟周期碰摩和干摩擦方向涡动，其中干摩擦方向涡动由于危害性最大受到了学者们的重点关注。Black[69]早在20 世纪60 年代就开始了反向涡动的研究，分析表明干摩擦反向涡动发生的频率范围在未耦合时的转-静子系统固有频率和转-静子系统耦合状态下的固有频率之间，并给出了基于频率响应函数预测转子反向涡动边界的方法；Zhang[70]、Grandall 等[71-72]和Lingener[73]在理论和试验方面进一步开展了深入研究，验证了Black 的相关分析结论；Childs等[74]进一步将Black 的分析方法推广到多模态转子中，并对Bartha 的试验模型进行了预测，预测所得系统涡动频率与试验结果非常接近；江俊[75-76]在反向涡动的理论方面也开展了较多工作，基于2 自由度或4自由度碰摩模型，解析确定了无碰摩、同步全周碰摩、拟周期碰摩和干摩擦反向涡动4 类运动的存在边界，并进一步结合碰摩转子在升速过程中轴心轨迹、幅频响应进行详细计算和分析，研究得出了升速过程中质量不平衡诱发转子反向涡动的物理机制[77]；Hong等[78]提出复非线性模态引入碰摩转子分析，从非线性模态的稳定性角度揭示了碰摩转子反向涡动发生机理。

碰摩附加约束下转子动力学特性是碰摩研究中的另一个重点，其是由于转子与静子一直接触或者持续的间断接触而导致转子系统刚度增加的现象。利用该现象，Chu 等[79]建立了在碰摩过程中转子系统刚度的参数识别方法，将其应用于碰摩转子的故障诊断；Wang 等[80]分析了碰摩约束对转子动力学特性的影响，指出附加约束刚度使转子共振区间扩张，并出现不稳定接触区域；Abuzaid 等[50]指出碰摩可以引起转子系统刚度产生时变特征，甚至导致不稳定现象，并通过试验和仿真研究了其对转子振动特性的影响；基于Floquet 理论，Hong 等[81]研究了间歇碰摩状态下柔性转子系统的模态特性；Yu 等[82]在非线性模态理论框架下对碰摩约束问题开展了系统研究，首先基于简单理论模型转子，研究了附加约束对转子模态频率、模态稳定性及模态振型的影响，其次结合碰摩转子响应变化规律，揭示了非线性模态与典型碰摩响应的内在关联，进而提出了基于非线性模态的转子共振响应预测和反向涡动响应预测方法[83]，进一步，将上述方法拓展到典型航空发动机柔性转子和双转子系统，研究了碰摩影响下的转子非线性模态特性[48,84]。

3.2 转子碰摩的弯扭耦合振动响应

发动机低压转子轴（图1）细长且两端含大质量叶盘，扭转模态频率较低且与弯曲模态频率接近。当碰摩发生时，转子不仅会产生扭转振动，并可能在不平衡等因素影响下与横向弯曲振动发生耦合振动，导致复杂弯扭耦合响应甚至动力学失稳。

早在20 世纪80 年代，Bernasconi[85]就发现不平衡会引发转子弯扭耦合振动问题；Al-Bedoor[86]、Huang[87]、何成兵[88]、刘占生[89]围绕不平衡转子的弯-扭响应特征及耦合振动机理开展研究，发现耦合效应所导致的弯曲和振动响应中会存在1X、2X、3X 转频成分，并可能出现组合共振现象；Hong 等[90]从模态角度发现了不平衡转子的弯曲-扭转模态耦合现象及由此导致的振动失稳；近期，Wang 等[91]采用理论与试验结合研究了不平衡激励下多盘转子-支承-联轴器系统的弯扭耦合振动特性。

上述工作仅考虑不平衡影响，部分学者围绕碰摩转子的扭转振动和弯扭耦合亦开展了研究。Edwards等[92]首次考虑碰摩导致的扭转振动，分析了扭转振动对转子弯曲振动的影响，表明当转子运行在扭转固有频率点时，其轴心轨迹相比不考虑扭转时更为复杂；Patel 等[93]以Jeffcott 转子为对象，同时考虑转子、静子的平动和转动自由度，采用能量法建立了其动力学方程，指出不平衡质量和碰摩力是转子发生弯扭耦合的必要条件；Vlajic 等[94-96]建立了悬臂转子模型和相应的转子试验器，详细研究了正向全周碰摩-反向涡动时转子扭转振动特征，理论揭示了碰摩摩擦对转子扭转振动稳定性的影响；基于接触动力学理论，Mokhtar 等[97]建立了转静子碰摩的弯扭耦合动力学模型，获得了转子轴心轨迹、横向-扭转时频响应及碰摩力变化规律；Yang 等[98]研究了叶尖-机匣非均匀间隙情况下转子系统碰摩弯扭耦合响应，表明非均匀间隙情况下转子碰摩通常更为剧烈，严重危害转子稳定运转。

3.3 叶片-机匣的碰摩振动响应

对于叶片和机匣碰摩，除了从转子动力学角度分析转子涡动特性外，另一个研究热点是叶片和机匣自身的复杂动力学特性。在航空发动机中，特别是高涵道比涡扇发动机风扇部位，叶片和机匣直径大、刚度弱，碰摩时叶片和机匣的振动问题尤为突出。与转子动力学研究中多将叶片-机匣简化线性或非线性的刚度单元不同，在叶片-机匣碰摩分析中需要精确考虑叶片和机匣的结构动力学特征，如宽弦叶片的复杂弯曲-扭转模态、机匣的节径型振动等，因此通常借助有限元法或连续体振动理论建立叶片和机匣的动力学方程。目前，叶片-机匣碰摩研究主要包括不同碰摩参数或形式下叶片-机匣振动响应以及碰摩导致的叶片-机匣系统耦合振动。

3.3.1 叶片-机匣振动响应

在针对叶片-机匣振动响应的研究中，刘书国[32]数值仿真研究了某高压涡轮叶片-机匣碰摩的瞬态动力学过程，讨论了叶片和机匣的动态响应及应力波在结构中的传导特征；采用相似方法，张俊红[34]进一步分析了封严涂层对叶片-机匣碰摩过程的影响；马辉等[99-100]通过ANSYS 软件建立了考虑榫连接的叶盘有限元模型，采用脉冲力模拟碰摩载荷，分析了不同碰摩参数下叶片响应和榫连接接触特征；Zeng[31]和Guo 等[101]等考虑叶片和机匣复杂振动模态，研究叶片-机匣系统的混合单元建模和半解析建模方法，据此分析了转速、叶盘参数等对叶片、机匣振动响应的影响。近年来，随着发动机叶片向3 维设计转变，叶片结构造型更为复杂，这一定程度上会放大碰摩的非线性效应，因此，诸多学者对宽弦风扇叶片与机匣的碰摩振动问题开展了研究。柴向海[33]建立了宽弦风扇叶片叶尖刮蹭显式动力学分析模型，分析了叶片与机匣刮蹭后叶片变形及机匣损伤规律；陈大玮[39]研究了宽弦风扇叶片参数化建模，并利用碰摩动力学研究了叶片造型对于机匣碰摩振动的影响规律；Piollet等[102]基于NASA Rotor 37 建立了叶片-机匣碰摩的数值仿真方案，比较了不同叶片弯掠方式下系统碰摩动力学特性，为叶片造型设计提供了重要参考。

3.3.2 叶片-机匣系统耦合振动

当叶片和机匣持续碰摩接触时，振动能量通过碰摩相互作用在叶片和机匣系统不断传递，能够导致叶片-机匣系统的节径型耦合振动，称为模态耦合作用（Modal interaction），如图10所示。

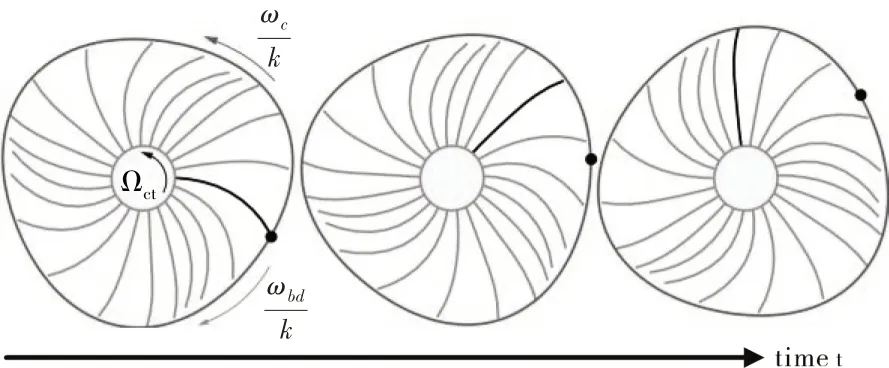
图10 碰摩作用下叶片-机匣系统的3节径耦合振动

对于模态耦合作用的产生，研究指出叶片和机匣的行波波速须满足一致性条件[103]

式中：ωc,k为机匣节径数为k时的模态频率；ωbd,k为叶片节径数为k时的模态频率；Ωc为转子转速。

式（6）对应着3 种可能的耦合条件，根据叶片、机匣自身的固有特性以及发动机工作转速范围，Ωc=(ωc,k+ωbd,k)k这一情况在实际工作中最有可能出现，需要予以重点关注，而另外2 种情况通常发生在低转速，可不考虑。当发生模态耦合作用时，叶片和机匣系统振动响应通常会不断发散，危害性极大。Schmiechen[104]建立了2 维叶片-机匣有限元模型，研究了系统耦合振动响应，研究发现在转静子耦合共振转速附近，响应振幅将随时间逐渐增大；Legrand 等[28]基于类似的模型发现叶片-机匣碰摩系统的耦合振动响应有衰减、持续和发散3 种形式，如图11 所示；曾振坤等[105]建立了增压级叶片-机匣耦合系统的4 自由度动力学模型，通过仿真分析发现，转静系统耦合振动通常在某一转速区间发生失稳，且通常略高于Ωc=(ωc,k+ωbd,k)k这一判别条件给出的转速点。

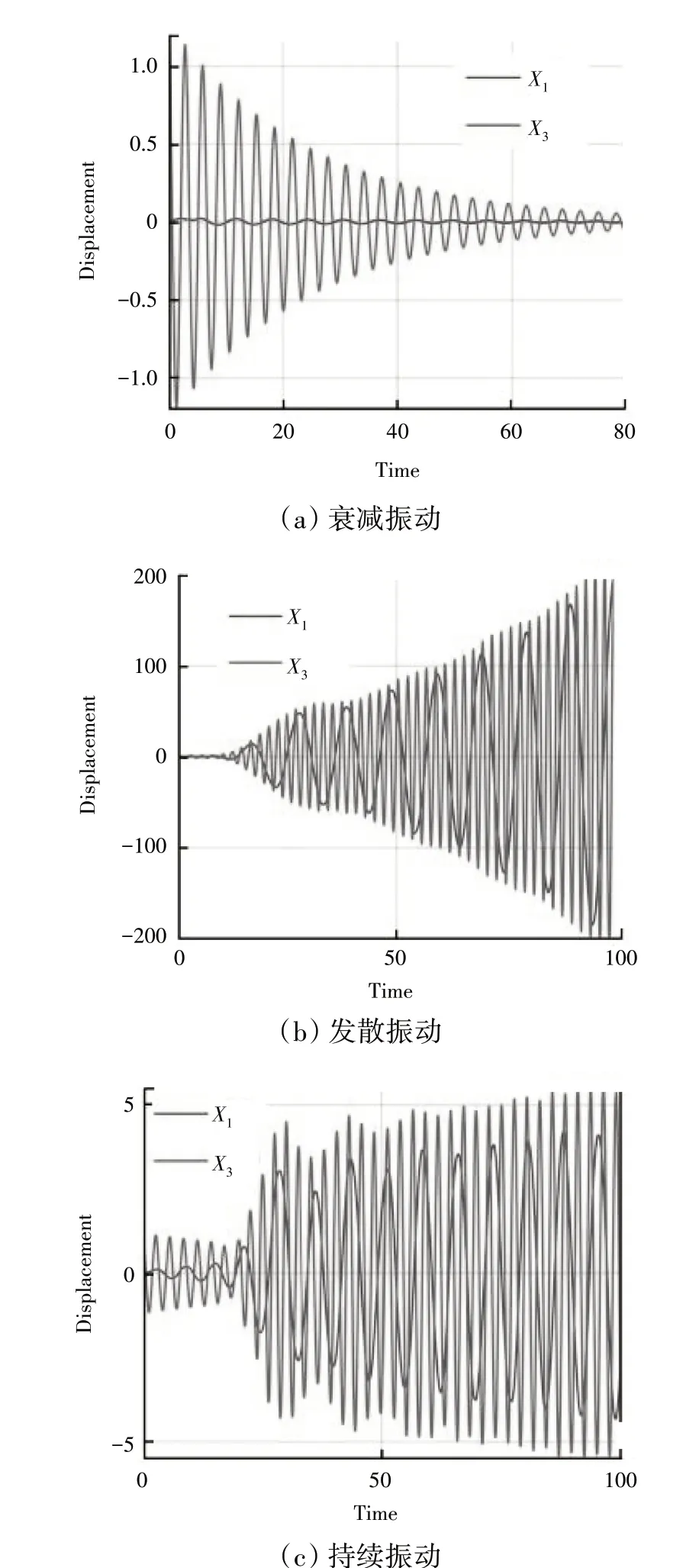
图11 叶片-机匣碰摩系统的3种耦合振动形式

3.4 旋转壳碰摩的振动响应

在发动机中存在大量旋转薄壁结构（即旋转壳体），这些薄壁壳与静子叶片或封严结构的间隙极小，工作中容易发生旋转壳和静子件碰摩，如图1 中增压级鼓筒与静子叶片碰摩。与转子轴相比，薄壁壳体径向刚度更弱，除随转子轴发生横向振动，主要表现为周向正弦波的振动，即节径型振动，如图12 所示。因此，碰摩作用下旋转壳具有更复杂的振动特征和需要关注的特殊力学问题，包括碰摩引发旋转壳节径型共振或与静子件的耦合共振、不同碰摩形式下壳体复杂行波振动及振动稳定性、碰摩激励下转子轴横向与壳体径向的耦合振动等。

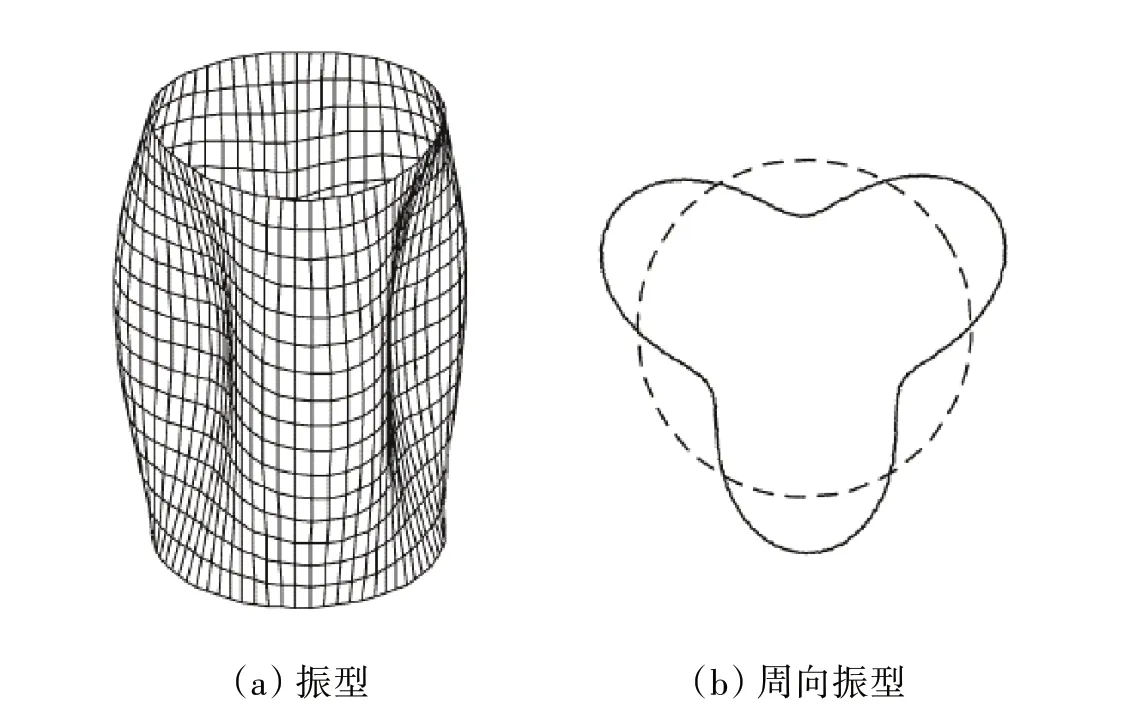
图12 薄壁壳体的3节径模态振动

目前，旋转壳的研究多集中在其自由振动和强迫振动方面。1890 年，Bryan[106]首次提出转动薄壁圆柱壳存在行波振动的现象，此后该现象得到了诸多学者研究，极大促进了旋转壳振动理论和分析技术的发展；Srinivasan[107]以无限长的转动圆柱薄壁壳为对象，系统研究了其行波振动特性；Saito 和Endo[108-109]着眼于有限长转动圆柱壳开展研究，他们还搭建了两端简支鼓式转动件试验台，理论试验研究了壳体前后行波频率特性；在中国，洪杰等[110]建立了求解旋转薄壁壳体行波振动频率的传递矩阵法，通过试验验证了方法正确性，还系统分析了长径比、厚径比及边界条件等结构参数对旋转壳体行波振动特性的影响规律[111]；在外载荷激励下转子强迫响应方面，Huang等[112-113]较早的针对两端简支的旋转圆柱壳开展了研究，首先理论推导建立了类似于模态叠加思想的壳体振动响应求解方法，而后着重分析和讨论了科氏力对壳体强迫振动的影响以及平移正弦载荷下旋转圆柱壳的共振现象；Gong 等[114]通过单脉冲形式的载荷模拟碰撞冲击作用，研究了碰撞载荷下旋转层合壳的瞬态响应，但研究结果未体现旋转壳的行波振动特征；李健等[115]吸收Donnell 壳体振动理论，利用复分析方法研究了旋转薄壁悬臂壳圆柱壳在法向激励下的行波振动；Wang等[116]研究了悬臂形式的旋转圆柱壳在简谐激励作用下的非线性动力学响应；然而，李健和Wang的研究中均未能很好的考虑壳体转动效应带来的影响。

虽然对旋转壳体振动理论的研究已经取得了较大进展，但针对碰摩作用下旋转壳动力学特性的研究还极为欠缺。刘伦等[117-118]建立了点碰摩和偏摩状态下鼓筒碰摩振动微分方程，研究了激励频率、碰摩刚度、间隙等参数对鼓筒碰摩响应的影响规律；Zhang等[119]报道了某发动机风扇鼓筒与第1 级静叶的碰摩故障现象和相应振动信号特征，从转子和鼓筒的固有特性角度对碰摩故障做了一定解释，但未深入研究旋转鼓筒受碰摩影响时的响应特征；近年来，韩清凯等[120-121]的理论与试验研究了旋转鼓筒在碰摩激励下的非线性振动响应，但仅局限在固定点碰摩这类简单的碰摩形式，对碰摩载荷的模拟采用的是较为理想的周期脉冲载荷。

3.5 碰摩的其他问题研究

发动机的碰摩热效应和轴间碰摩也需关注，但相关研究报道相对较少。

碰摩热效应方面的研究多关注摩擦热弯曲转子动力学行为和稳定性，该问题多发生在转轴与封严件配合位置。摩擦产生的热量进入转子，导致转子截面沿径向的温度分布不均匀，转子局部发生不均匀膨胀进而产生热弯曲，热弯曲对转子产生附加不平衡量，其与转子初始不平衡叠加导致系统动力学响应发生变化。1980 年，Kellenberger[122]提出了针对碰摩热效应的分析模型，能够有效分析转子内热量传递以及由此导致的热弯曲变形，并发现转子弓形弯曲致使转子发生螺旋运动。本质上，碰摩热效应导致的转子振动属于热力耦合问题，但由于温度场分析的时间尺度显著高于动力学分析的时间尺度，实际时通常将其处理为弱耦合甚至直接解耦的思路进行分析，例如：Goldman 等[123]采用平均法分析了摩擦热弯曲转子系统的稳定性问题；姚红良等[124]分析时将摩擦热弯曲转子系统振动作为分段慢变振动来考虑。在研究对象上，部分学者围绕着实际旋转机械的碰摩热效应问题开展研究，例如：黄葆华等[125]、Bachschmid 等[126]分析了压缩机转子、汽轮机转子的热弯曲响应，这些研究中多通过传递矩阵法或有限元法建立转子系统结构场模型，采用2维或3维定量分析方式计算热场。

航空发动机多采用并列双转子结构，细长低压转轴穿过高压转子，高低压转轴间通常还设计各种封严结构防止气体泄漏，因此，轴间碰摩也是航空发动机中不可忽视的一种碰摩类型。早在20 世纪80 年代，NASA 研究就指出在叶片丢失等恶劣工况下，不仅要关注转静件碰摩，转子和转子轴间碰摩问题亦需要关注[127]；某涡轴发动机、某涡扇发动机在试车过程中均发生过轴间碰摩问题[128-129]。近期，Yu[130-131]以独立支承的某发动机双转子系统为对象，建立了轴间碰摩动力学模型，较为细致的讨论了轴间碰摩下转子运动状态、时频响应特征以及转速大小、方向对系统动力学行为的影响。发动机高、低压转子不仅转速大小不同，还可能存在反转情况，同时分布在高、低压转子上的不平衡激励频率也不一样，高低压转子涡动状态也存在差异。以上使得轴间碰摩时的碰摩力变化规律远比转静碰摩复杂，振动能量在双转子之间的传递过程也更加复杂，导致轴间碰摩表现出诸多不同的动力学行为，不过目前针对轴间碰摩的研究报道极为有限，有待进一步深入分析。

4 总结与展望

碰摩是一类涵盖多物理场、多尺度和强非线性的复杂力学问题：多物理场，主要指热-机械耦合，源于碰摩过程中的冲击、摩擦及摩擦热效应；多尺度，细观层面上体现的是局部接触、摩擦磨损、热效应及其导致的碰摩力复杂变化规律，宏观上则是转静系统整体动力学行为；强非线性，由于转静件间隙、摩擦甚至是碰摩过程中局部接触区域的塑形变形导致，这将引起结构系统的超谐波、亚谐波甚至分岔和混沌等行为。以航空发动机为背景，半个多世纪以来国内外学者围绕碰摩问题取得了极为丰硕的研究成果，但面向解决发动机研制过程中所遇到的实际碰摩类工程问题，在理论方法等方面仍有不足，建议未来工作重点如下：

（1）在碰摩的局部力学行为分析与载荷特征方面：无论是发动机中的叶片-机匣还是篦齿封严，其均有着复杂的结构特征，并且静子表面通常附有蜂窝涂层或者其他材质涂层。目前，对叶片-机匣、篦齿封严等结构件在碰摩过程中的摩擦磨损机制、局部接触区域的损伤特征及碰摩热耦合效应等缺乏深入研究，蜂窝等涂层结构对局部力学行为及碰摩载荷特征的影响尚未明确，因此已建立的诸多碰摩力模型缺乏针对性，在应用到发动机碰摩分析时缺乏精度和说服力。有必要充分考虑发动机碰摩件实际结构、各类涂层结构及其材料特性，开展多物理场建模仿真和机理试验研究，深入分析碰摩过程中的碰摩力、热效应以及局部磨损和损伤特征，明确转静件相互作用的力学特征并把握主要的影响因素，在此之上发展更为有效的碰摩载荷模型，以更好的描述碰摩过程中的载荷特征。

（2）计及局部力学行为的跨尺度力学模型建立与求解技术方面。碰摩冲击、摩擦磨损及摩擦热效应属于细观尺度的问题，需要在细观尺度层面建立精细的力学模型予以描述；而叶盘及转子系统的动力学响应属于宏观尺度的问题，通常通过建立高维的有限元模型进行刻画，显然，二者属于不同空间尺度。目前分析中，多将碰摩视为分段形式的线性或非线性力引入到结构动力学计算中，显然这种简化不能很好的反映碰摩局部力学行为带来的影响；但若对整体结构直接采用精细单元建模，并在碰摩局部开展热-力-磨损仿真求解，又会导致模型规模过大，带来难以克服的求解难题。在碰摩局部多物理场仿真模型及转静子整体动力学模型基础上，通过引入等效平均或借鉴多尺度分析思想等，开展能够有效反映局部力学行为的跨尺度力学模型建模方法，并结合自由度减缩方法发展高效的求解技术，以适用于发动机转静件碰摩的定量分析。

（3）在转静件的碰摩动力学行为上，当前对转子系统碰摩作用下的横向动力学特性研究成果最为丰富，不过发动机中转静件类型多、载荷工况也更为多样，还有诸多的理论问题需要研究。一是针对发动机柔性转子和双转子，研究揭示常规载荷、极限载荷等各类载荷工况下，由转静碰摩、轴间碰摩诱发的动力学失稳机理（既包括横向的自激振动失稳，也包括弯扭耦合振动失稳），并发展相应的分析方法；二是围绕着叶片-机匣、旋转薄壁壳体的碰摩，考虑薄壁结构件的节径型模态特征，研究高柔度薄壁结构在碰摩作用下的耦合振动特性，包括耦合振动形式及发生条件，特别是要深入揭示由于节径型模态耦合导致的振动失稳机制并建立相应的失稳判别方法。

（4）面向航空发动机工程需求，还需发展转静件碰摩的损伤评估方法和危害度评价方法。从局部力学行为上讲，冲击、摩擦及热效应导致局部的磨损损伤，影响关键构件的结构完整性，特别是叶片，可能在叶尖处发生局部裂纹、掉角等损伤，但针对这些关键构件特别是叶片，目前还缺乏有效碰摩冲击损伤分析和评价方法；从整体力学行为上讲，碰摩能够导致系统亚谐波、超谐波共振，严重时甚至使系统发生动力学失稳，目前在发动机间隙设计时为保证较高气动效率，在台架试车时通常允许一定程度的碰摩，但多基于工程经验确定允许的转静切入量，目前仍然缺乏工程适用的定量分析方法，对碰摩的危害度予以评价和界定，以此指导工程设计。