降低FBMC-OQAM系统中PAPR的GA-IBPSO算法
2023-05-12朱海云马天鸣江潇潇王春媛
朱海云,马天鸣,江潇潇,王春媛
(上海工程技术大学 电子电气工程学院,上海 201620)
1 引 言
滤波器组多载波(Filter Bank Multi-Carrier,FBMC)属于一种新型的非正交多载波调制技术,它采用对子载波进行滤波的方式来进一步抑制信号的带外频谱泄漏,同时由于系统运用了偏移正交幅度(Offset Quadrature Amplitude Modulation,OQAM)的调制方式,使得子载波之间只需满足在实数域上保持正交,获得了波形时域上的设计自由度并能够更灵活的适应信道的变化,同时还大大降低了在时频同步上的需求.因此较之正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM),FBMC更能满足当前5G通信的一些关键需求.
但是FBMC-OQAM在实际应用中也存在着一些不足之处,其中之一就是它和OFDM一样具有较高的信号峰均功率比(Peak-to-Average Power Ratio,PAPR)[1].然而FBMC-OQAM相邻数据块之间具有时域重叠特性,因此把OFDM中降低PAPR的方案直接移植到FBMC-OQAM中将难以获得良好的抑制效果.目前大部分降低FBMC-OQAM中PAPR的方案都是在OFDM中方案的基础上进行改进,使之能够适应FBMC-OQAM.文献[2]设计一种TR-μLaw抑制FBMC-OQAM中的PAPR的技术,该方法将载波预留(Tone Reservation,TR)和μ-Law压扩技术融合起来,促使两种方法的利弊互补,但是算法的复杂度较高.文献[3]设计了一种预编码技术,该技术基于修剪的离散傅里叶变换和单抽头缩放,结合了FBMC-OQAM和单载波频分多址(single carrier-frequency division multiple access,SC-FDMA)两者各自的优点,但是编解码的过程比较复杂.文献[4]在传统迭代部分传输序列(Iterative Partial Transmit Sequence Algorithm,IPTS)算法的基础上,通过将相位因子向量分为奇偶分别进行迭代,扩大了搜索范围,系统的 PAPR得到了明显的抑制,但是计算量较大.在这些PAPR抑制方案中,由于PTS技术在优化组合符号子块的同时对子载波数量没有限制,而且在信号无失真的情况下PAPR进行抑制,因此成为了当前最有吸引力和最有效的抑制方案.
考虑到寻找最佳相位组合以减小PAPR的穷举搜索的计算复杂度会随着子块的数量而增加,目前国内外的学者已经提出了一些智能优化算法应用于PTS的方案.文献[5]提出了一种基于遗传算法(Genetic Algorithm,GA)的双层部分传输序列方案,与传统方案相比可以在显著降低计算复杂度的同时获得更好的PAPR抑制效果,但在搜索后期效率较低.文献[6]设计的基于奇数分割的PTS新方案,并引入了含比例因子的粒子群优化(Particle Swarm Optimization,PSO)算法,在抑制PAPR的同时降低了计算复杂度,但在搜索后期容易陷入局部最优.
本文设计了一种改进的离散二进制粒子群优化的遗传算法(Genetic Algorithm -Improved Binary Particle Swarm Optimization,GA-IBPSO),它通过选用带外衰减性能更好的原型滤波器来代替原有的PHYDYAS(European Physical Layer for Dynamic Access)滤波器,并将遗传算法(Genetic Algorithm,GA)中的选择交叉、变异操作融入到采用双层部分传输序列(Bilayer Partial Transfer Sequence,BPTS)思想进行改进后所得到的IBPSO算法中.理论分析与仿真结果表明,与BPSO算法相比,GA-IBPSO算法虽然计算复杂度略微增加但获得了更好的PAPR抑制性能.
2 FBMC-OQAM系统结构
FBMC-OQAM系统的发送端,经过OQAM调制和串并转换后,在t时刻的基带发送信号可表示为[5]:
(1)
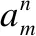
为了估计离散时间信号真实的PAPR值,以t/L采样率对FBMC-OQAM信号S(t)进行采样,其中L=KN,K为重叠因子,N为子载波个数.因此采样后的离散时间信号S(k)可以表示为[7]:
(2)
其中h(k)为PHYDAYS滤波器.PHYDAYS滤波器是当前FBMC-OQAM系统中使用最广泛的原型滤波器,满足近似完美重建(Near Perfect Reconstruction,NPR)条件.由式(2)不难发现,S(k)的结构具有时域重叠特性,其PAPR表示为[8]:
(3)
3 基于IDPSO-BPTS的PAPR抑制算法
3.1 改进的原型滤波器
鉴于FBMC-OQAM采用了原型滤波器的缘故,因此它的信号较之OFDM而言具有更好的相邻带外泄漏抑制特性.在进行PAPR抑制之前,可以通过直接优化滤波器系数的方案设计出一种新的原型滤波器h1(k).优化的主要方法为:将阻带区域能量最小作为优化的目标函数,分别把原型滤波器的对称性、Nyquist第一准则、载波间干扰(inter-carrier interference,ICI)和符号间干扰(inter-symbol interference,ISI)小于引入的门限值作为约束条件,求解出最优的滤波器的系数.
假设设计的原型滤波器h1(k)是对称的并且满足实际信道中的NPR条件,滤波器长度为Lp,其中Lp=KN-1.经过傅里叶变换,滤波器h1(k)的传输函数可以表示为:
(4)
为了实现对旁瓣能量的抑制和降低旁瓣泄漏,不妨用P表示阻带区域的能量,它的表达式为[4]:
(5)

对h1(k)做重叠取样离散化处理,即h1(k)=[h1(0)h1(1)…h1(Lp-1)]T,此时式(5)可以进一步表示为:
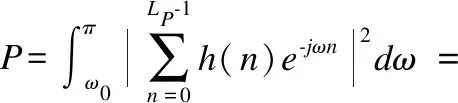
(6)
限制条件1:原型滤波器的对称性:
h1(k)=h1(Lp-1-k)
(7)
限制条件2:Nyquist第一准则:
(8)
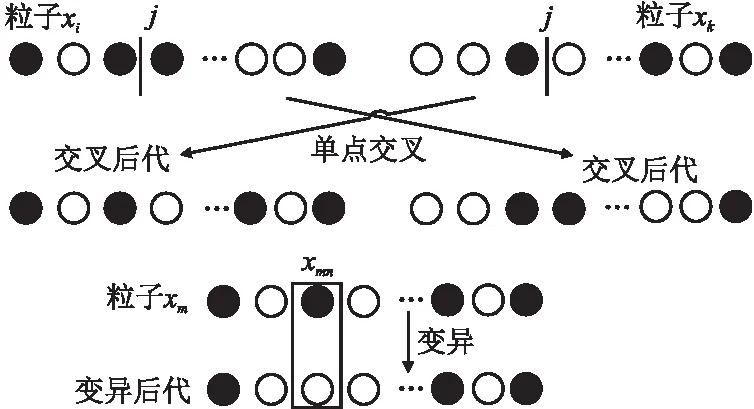
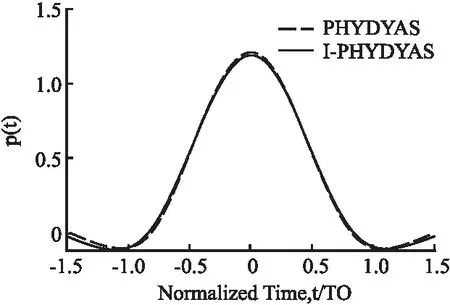
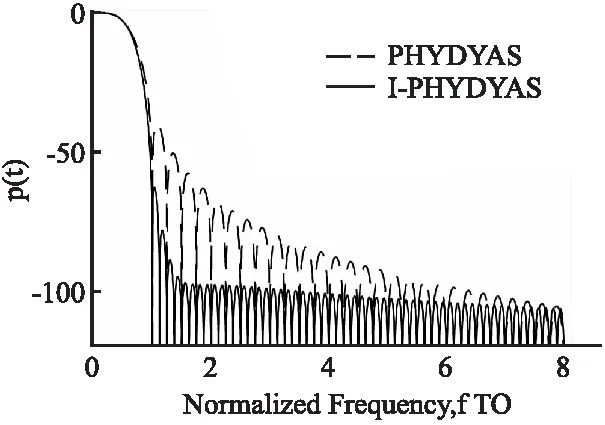
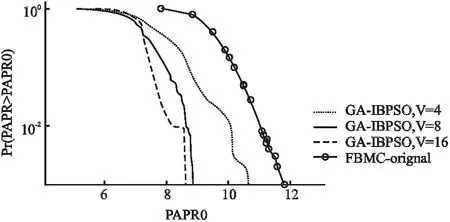
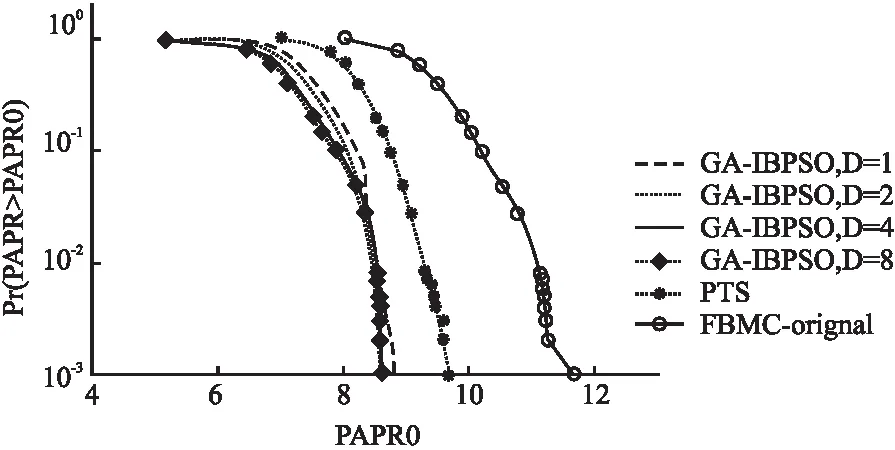
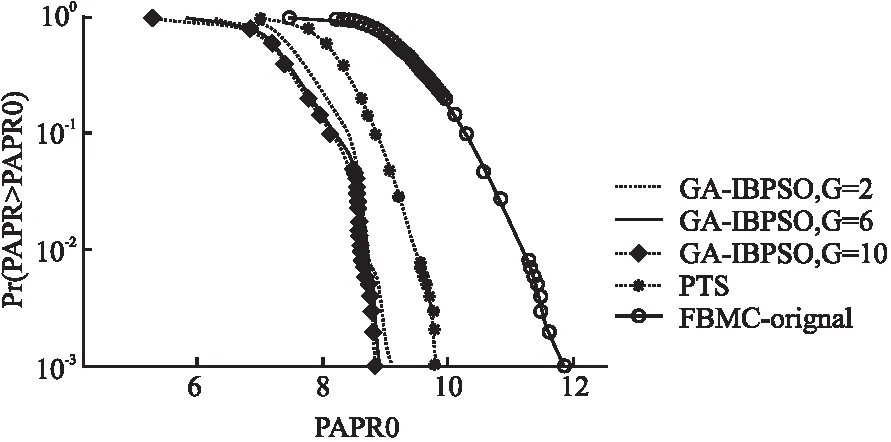
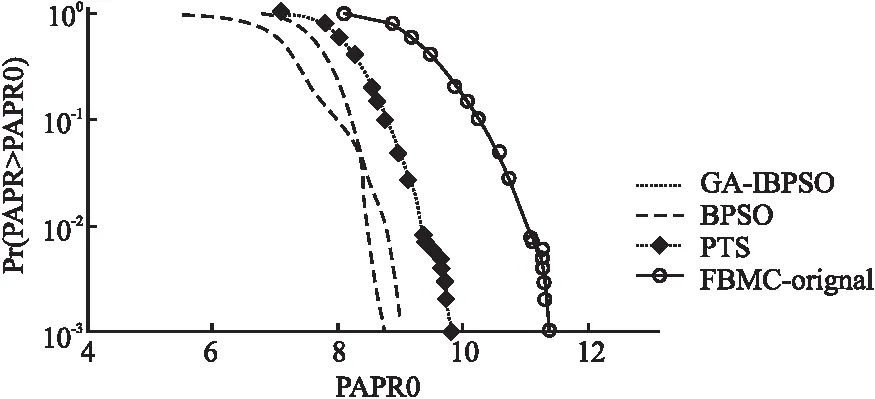
限制条件3:ISI/ICI的能量 (9) 采用直接改进滤波器系数的方法,将上述滤波器的设计问题转化为数学优化问题,根据优化目标式(6)以及约束条件式(7)~式(9)可知这是一个非线性优化问题,这里采用序贯二次规划法[9],解出即可得到设计的原型滤波器h1(k). 3.2.1 双层部分传输序列(BPTS) (10) BPTS是在原有PTS的基础上将N个子载波数据先后分成两层:第1层将N个子载波划分为V个不相交的子数据块,进行第1次最佳相位因子的搜索;第2层将V个子数据块再进一步分割成D个区块,再次搜索D个区块的最佳相位因子.BPTS的模型如图1所示. 图1 BPTS算法模型Fig.1 Model of BPTS algorithm 3.2.2 GA-IBPSO算法 J.Kennedy和R.C.Eberhart提出的粒子群优化算法(Particle Swarm Optimization,PSO)[10].PSO主要是基于连续区间进行搜索,考虑到一些实际工程应用中待求解的变量不是连续的.对此,J.Kennedy和R.C.Eberhart又提出了二进制粒子群优化(Binary PSO,BPSO)算法,主要用来优化离散空间约束问题,BPSO有记忆,且具有原理简单、参数少、容易实现等优点[11]. 然而传统的BPSO存在两个缺陷:1)算法中的惯性权重w为固定值,而w决定了对粒子当前速度的继承有多少,w偏小时算法的全局搜索能力较差,w偏大时算法局部搜索能力较差[11];2)BPSO算法计算精度不高.对此本文提出了GA-IBPSO,首先采用非线性的动态惯性权重系数公式,让惯性权重根据粒子适应度值动态改变,调节算法在全局和局部搜索的水平,进行初步寻优,然后将GA算法的选择、交叉和变异等操作融入到BPSO中.由于GA具有简单、通用性强、鲁棒性好、适用于并行分布式处理等优点[12],可以进一步改善BPSO容易陷入局部最优解的问题,同时提高算法的优化效率和运算精确度.GA-IBPSO的关键算法步骤如下: (1)初始化粒子群,包括位置x和速度v,以及种群大小Np=30,迭代次数G=4,加速度常数c1=c2=2,比例因子γ动态地从0.5变化到5[11]; (2)通过函数式(10),计算每个粒子的适应度函数; (3)计算当前个体极值(Pbest)和群体极值(Gbest),Pbest是粒子所经历位置中得到最优解的位置,Gbest是整个种群中粒子搜索到的最优解的位置; (4)分别更新每个粒子的速度和位置. 1)首先更新粒子速度,可以表示为[11]: (11) 其中i表示粒子的索引,n表示迭代的次数,v表示粒子速度,r1、r2代表均匀分布在 [0,1]中的随机数,pi代表第i个粒子之前的最佳位置,g表示为粒子群中最优粒子的位置,xi表示第i个粒子的位置.自适应惯性权重w的调整公式表示为: (12) 其中f代表当前适应度值,favg为平均适应度值,fmin为最小适应度值,惯性权重wmax=1、wmin=0.4. 2)然后采用优化稳定的sigmoid函数将速度映射到[0,1]区间,作为粒子下一步取值为1的概率[11],可以表示为: (13) 3)再将粒子通过式(14)实现位置的绝对变化:当前位值由1变化为-1,或者由-1变化为1. (14) 其中rand表示[0,1]的随机数. (5)增加遗传算法(GA)操作,提高种群多样性和全局搜索水平.交叉和变异的操作如图2所示,其中黑球代表1,白球代表-1. 图2 粒子的交叉、变异操作Fig.2 Operations of the crossover and mutation 1)首先采用轮盘赌法选取适应度值较小的优秀粒子,自适应性选择概率表示为[12]: (15) 其中Fi=k/fi,fi为适应度值,k为常数,N为种群个数; 2)然后采用单点交叉法为粒子xi和粒子xk在位置j处进行交叉操作,交叉概率pc可以表示为: (16) 其中kc为[0,1]之间的常数,f为粒子xi与xk两个粒子中较大的适应度,favg为平均适应度值,fmax为当前最大的适应度值; 3)选择粒子xm的第n个因子xmn进行变异,变异概率pm可以表示为: (17) 其中km为[0,1]之间的常数,且km远小于kc,f′为粒子xm的适应度,favg为平均适应度值,fmax为当前最大的适应度值; (6)满足最大迭代次数的条件后,输出最优个体,否则返回步骤2)继续执行. 本节进行MATLAB编程仿真,首先将3.1中提出的改进原型滤波器h1(k)与PHYDAYS滤波器h0(k)进行性能仿真对比,然后对基于h1(k)的FBMC-OQAM系统采用控制变量法就3.2.2中提出的GA-IBPSO算法中的几个变量参数逐一进行仿真并确定,再对参数确定后的GA-IBPSO算法和传统算法一并进行PAPR性能仿真.仿真相关参数的设置如表1所示.鉴于5G通信信道同时具有多径和时变性的特点,这里选取相对延时较为明显的ITU-VB[13]作为系统仿真时的无线信道模型. 表1 Matlab仿真参数Table 1 Simulation parameters of Matlab 首先,对两种原型滤波器自身的性能进行比较.当K=4、L=256时,h0(k)和h1(k)的脉冲响应和归一化响应分别如图3和图4所示.从图中不难看出,与h0(k)相比,h1(k)的阻带能量抑制有显著改善,这是由于最小化原型滤波器阻带能量、限制载波间干扰和符号间干扰所设计的h1(k)能够有效地减少带外能量泄漏,并且所提出的方案在FBMC-OQAM系统中实现了定向旁瓣能量抑制. 图3 滤波器h0(k)和h1(k)的脉冲响应Fig.3 Impulse responses of the filters h0(k)and h1(k) 其次,选用h1(k)进行预处理,对几种抑制算法的PAPR性能进行仿真比较.由于PAPR是随机的,于是通常运用互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)来描述FBMC-OQAM的PAPR的性能,它表示计算PAPR大于某一门限值 PAPR0的概率,其定义式为[13]: 图4 滤波器h0(k)和h1(k)的归一化幅度响应Fig.4 Normalized magnitude responses of the filters h0(k)and h1(k) CCDF(N,PAPR0)=Pr{PAPR>PAPR0}=1-(1-e-PAPR0)N (18) 其中N为FBMC-OQAM的子载波数,PAPR0为某一确定的PAPR值.显然CCDF越小,则系统的PAPR的性能越好.为保证仿真结果的可靠性,这里将实验仿真次数设置为1000.整个PAPR仿真可以分为如下两个阶段: 1.保持参数K=4、L=256、N=64、Np=30固定不变,采用控制变量法逐一分析参数V、D、G分别发生变化时,对GA-IBPSO算法的PAPR性能所造成的影响. (1)假定D=4、G=6,当V分别取4、8、16时,即将数据分别分成4、8、16个不相交的子块时,对GA-IBPSO算法的PAPR性能进行仿真,仿真结果如图5所示.在CCDF=0.001的情况下,V=4时,系统抑制PAPR的性能较差,V=8时性能较之前提高了1.707,V=16时性能获得了进一步提高但不明显.这是由于子块数量V的增加会使得加扰的子块数目随之增加,能够进一步扩大GA-IBPSO算法的搜索范围,因此PAPR抑制性会有着明显提高.但V的增加也会造成复杂度的急剧增大,因此经过权衡考虑后在实际仿真中选择V=8较为合适. 图5 V取不同值对GA-IBPSO算法PAPR性能的影响Fig.5 PAPR reduction results of the GA-IBPSO algorithm with different V (2)在V=8的基础上假定G=6,当D分别取1、2、4、8时,即对这8个不相交的子块数据分别进一步划分为1、2、4、8个区块(其中D=1表示无需进行再次划分)时,对GA-IBPSO算法的PAPR性能进行仿真,仿真结果如图6所示.从图中不难发现,当V一定时,D越大,则搜索范围越广,因此PAPR的抑制效果也就越好,但是复杂度也会随之增加,因此经过权衡考虑后在实际仿真中选择D=4较为合适; 图6 D取不同值对GA-IBPSO算法PAPR性能的影响Fig.6 PAPR reduction results of the GA-IBPSO algorithm with different D (3)在V=8、D=4的基础上,当G分别取2、6、10时,即将GA-IBPSO算法的迭代次数分别取2、6、10时对其PAPR性能进行仿真,仿真结果如图7所示.结果表明,当迭代次数G在一定范围内增加时,由于搜索得到的最优解更稳定,PAPR降低性能更好,但是计算复杂度也随之增加.同时也不难发现当算法的迭代次数达到6次以后,其PAPR性能将趋于稳定,因此经过权衡考虑后在实际仿真中选择G=6较为合适. 图7 G取不同值对GA-IBPSO算法PAPR性能的影响Fig.7 PAPR reduction results of the GA-IBPSO algorithm with different G 2.当K=4、L=256、N=64、Np=30、V=8、D=4、G=6时,将GA-IBPSO、BPSO、传统PTS、以及没有采用PAPR抑制 图8 GA-IBPSO与其他几种抑制算法的PAPR性能比较Fig.8 PAPR reduction results of the GA-IBPSO and other algorithms 算法时的FBMC-OQAM系统(FBMC-original)进行PAPR性能仿真,仿真结果如图8所示.由于本文提出的GA-IBPSO算法采用了BPTS来扩大搜索范围,同时将GA算法融入BPSO中来进一步优化相位因子,因此它较之其他算法来说可以获得更好的PAPR抑制效果. 接着对GA-IBPSO、BPSO、PTS这3种算法的计算复杂度进行比较.算法复杂度的改善通常采用计算复杂度减少率(Computational Complexity Reduction Ratio,CCRR)来进行衡量,其定义式为[14]: (19) (20) (21) (22) (23) +2(L+1)MN (24) +G(2D-1)(NP+1) (25) 表2 GA-IBPSO与BPSO、PTS的计算复杂度Table 2 Computational complexities of GA-IBPSO,BPSO,and PTS 表2给出了3种算法在N=64、V=8、D=4、G=2时各自的计算复杂度.从表中不难发现,尽管GA-IBPSO的计算复杂度较BPSO稍高,但相对于PTS来说计算量明显降低了许多. 本文提出了一种GA-IBPSO算法用来降低FBMC-OQAM中的PAPR,它将GA融入到BPSO算法中,并借助于改进的原型滤波器来进一步提升PAPR抑制能力.理论推导和仿真实验证明,相较于BPSO算法,采用所提出的GA-IBPSO方案通过计算量的略微增加,获得了更好的PAPR抑制效果.
3.2 基于BPTS的 GA-IBPSO群智能优化算法


4 仿真实验与结果分析
4.1 性能仿真和分析

4.2 计算复杂度分析
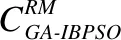

5 总 结
