重要特征选择和局部网络拓扑嵌入的社区发现算法
2023-05-12徐新黎肖云月龙海霞
徐新黎,尹 晶,肖云月,龙海霞
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
随着信息技术的不断发展与普及,出现了越来越多节点有属性的网络,例如社交网络Facebook、引文网络Wiki、在线商品评论网站Epinions、医学研究蛋白质网络等.社区发现是网络分析中的一个基本问题,对于属性网络来说,除了使社区内节点的连接紧密外,同一社区内节点的属性也应该是同质的,即同一社区内节点的特征信息相似.经典的社区发现方法主要分为两类:一类是仅处理网络的结构(即节点之间的联系),而忽略节点的特征;另一类是使用节点属性来发现社区,完全忽略节点之间的联系,代表方法有k-means聚类算法.近年来,国内外学者对属性网络社区发现的研究不断深入,注意到只处理结构或只处理属性的方法不能够完全利用网络中所有的可用信息,研究能同时利用结构和属性的社区发现方法已成为网络分析的一个新领域[1].
属性网络的节点规模一般比传统的复杂网络大,而且每个节点带有高维的属性信息.如何有效地处理大量的属性信息是一个难题,而特征选择是一个常用且可以较好地用于节点重要属性(特征)筛选的方法.通过特征选择可以剔除不相关的特征,降低节点属性的维度,但又不影响属性中有效信息的利用,可以协助分类、聚类、社区发现等下游任务的开展.常用的特征选择方法为无监督方法,例如拉普拉斯得分法LapScore,通过给属性网络中的每一个节点属性进行打分,筛选出分数最高的前t个节点属性[2].Li Z.等提出一种非负判别特征选择NDFS,利用判别信息和特征相关性来选择更好的特征子集,提出了一种简单有效的迭代算法来优化目标函数[3].对于链接社交媒体网络,Tang J.等提出一种特征选择框架LUFS,用伪标签作为无监督的替代约束,使用最大化模块度,并提出损失函数,用优化算法求解[4].为了利用节点属性有效减少噪声的链接对潜在表征的负面影响,Li J.等提出一种无监督的特征选择方法(NetFS),将潜在表征向量嵌入到特征选择阶段中,用优化算法求解后得到每个节点属性的重要性系数,从而筛选得到重要的节点属性[5].基于谱图理论,Zhao Z.等提出一种谱特征选择框架(SPEC),首先计算原始数据的相似性矩阵,然后计算每个特征的权重分数,利用权重分数判断特征的好坏[6].此外,考虑到特征矩阵和标签矩阵之间的共享公共模式,Hu L.等提出多标签特征选择方法(SCMFS),利用耦合矩阵分解(CMF)提取特征和标签之间的共享公共模式,并采用非负矩阵分解(NMF)来增强特征选择的可解释性[7].上述方法中,除了LUFS[4]和NetFS[5]结合网络链接信息进行特征选择外,其他方法都没有利用网络链接信息.
为了更好地在属性网络中实现社区发现,除了采用特征选择,还可以采用属性网络表征学习,来降低节点属性维度.和仅利用网络结构信息来获得低维度潜在特征的网络表示方法(DeepWalk[8]、LINE[9]等)不同,属性网络表征学习方法不但可以降低节点属性的维度,而且能够有效融合网络拓扑和属性信息.例如,Huang X.等提出一种通用的嵌入框架 (HILL),同时融合异构信息和拓扑信息,并且提出一种分布式算法(ADMM算法)完成优化求解[10].对于多视图网络,Wang H.等在2019年提出一种基于图的多视图聚类(GMC)方法,可以自动生成不同视图的权重,同时学习每个不同视图的图,并通过拉普拉斯矩阵对融合后的低维向量施加秩约束,可以自动生成聚类结果[11].Sun F.等提出了一个概率生成模型(vGraph)来协作学习社区成员和节点的低维表示,可以同时捕获图的全局结构和局部结构[12].Zhao Z.等在2021年提出了一种基于深度模型的属性网络嵌入学习方法(DeepEmLAN),通过深度注意力模型将不同类型的属性信息平稳地投影到相同的语义空间中,同时可以保持拓扑结构,使得有更多邻居的节点、有相似文本或者属性的节点在表示空间中更加接近[13].上述属性网络表征学习方法中,HILL算法没有深入融合网络拓扑的深层次信息,GMC方法对单视图网络的嵌入表示后的聚类效果明显比不上多视图的聚类结果,而vGraph和DeepEmLAN方法都需要标签信息进行训练学习.
为了以无监督的方式融合结构和属性进行社区发现,Zhang B.等在自动编码器框架中,提出了一种新的无监督社区检测图卷积神经网络方法(GUCD),引入了一个以社区为中心的双解码器,以无监督的方式分别重构网络结构和节点属性,还设计了一个局部增强的方案,以适应节点有更多的共同邻居和相似的属性与相似的社区成员[14].GUCD方法是在社区发现的同时融合结构和属性的,本文主要针对融合结构和属性之后进行社区发现.为了更好地处理节点属性的高维数据以及深入融合网络拓扑和节点重要属性,本文根据基于矩阵分解的特征选择和属性网络表示学习提出了一种社区发现方法,首先结合节点相似性提出联合相似度,用改进后的特征选择算法将网络中重要的属性筛选出来,然后将融合邻居信息的拓扑结构和重要属性联合建模,利用基于矩阵分解的属性网络表征方法求解得到节点嵌入向量,最后用聚类算法实现社区发现.实验结果表明所提算法具有较好的特征选择和划分社区的效果.
2 问题描述
一个既有链接信息又有节点属性信息的复杂网络可以表示为G=(V,E,X),其中V为含有n个节点的集合,E为链接边的集合,所有节点的属性可以用一个属性信息矩阵X∈Rn×m表示,m是属性类别个数.对于属性网络,一般图G为一个无向无权图,可以用eij∈E表示节点i∈V和节点j∈V之间的链接关系,如果两者之间有连边,则eij=1,否则eij=0.所有节点的连边关系就构成一个邻接矩阵A.
属性网络的社区发现是为了划分社区,即使同一社区内的节点连接紧密,且节点间的特征信息相似.为了更好地在属性网络中实现社区发现的任务,可以将网络中的每个节点的拓扑结构信息以及重要属性信息,以高效的方式映射到低维的表示空间中,得到节点的嵌入向量后进行社团划分.所以本文问题可以描述为:给定一个属性网络G=(V,E,X)及其邻接矩阵A,筛选出t个重要属性,与原拓扑结构组成一个新网络G′=(V,E,F),其中F∈Rn×t为重要属性信息矩阵,将网络G′的节点映射成低维向量后进行社区划分.
3 算法描述
3.1 算法框架
属性网络与传统网络相比,往往节点本身富含更多的信息.为了有效降低属性网络节点的维度,同时深入挖掘网络拓扑结构,将网络拓扑和节点重要属性进行有效融合,达到良好的社区发现性能,本文提出了联合重要特征选择和局部网络拓扑嵌入的社区发现算法(A Community Detection Method Combining Important Feature Selection and Local Network Topology Embedding,简称FSNE),算法整体框架如图1所示.

图1 FSNE算法框架图Fig.1 FSNE algorithm framework diagram
FSNE算法的第1步是基于节点联合相似度潜在表征的特征选择,首先计算节点的联合相似度,将基于联合相似度的节点潜在表征嵌入到特征选择过程中,筛选得到重要系数靠前的t个节点属性,与原网络拓扑组成新网络;第2步是用基于矩阵分解的网络嵌入框架将新网络映射成低维空间中的向量,首先计算融合邻居信息的拓扑相似度和重要特征的属性接近度,基于矩阵分解将拓扑结构和节点属性联合建模求解,得到融合了重要属性和网络拓扑的节点嵌入向量,最后使用k-means聚类算法进行社区划分.
3.2 基于节点联合相似度潜在表征的特征选择
特征选择可以将属性网络中节点的有效信息筛选出来,这里属性也称之为特征,通过去除不重要的特征,留下的节点特征集合就可以用来进行社区发现.基于网络拓扑建模的特征选择方法,一般只是单纯利用邻接矩阵进行建模得到潜在表征,但这样往往会造成网络结构深层次信息的缺失.因此,本文采用节点相似度以有效地融合网络结构的深层次信息,从而更好地辅助特征选择.
节点相似性指标可以用来作为社区划分的依据,不同的指标通常从不同的角度描述两个节点之间的相似程度,例如考虑共同邻居数的CN指标[15]、在CN指标上发展而来的Jaccard指标[16]和Sφrenson指标[17]、基于节点间局部点不重复路径的SLP指标[18]等.在复杂网络中,Jaccard相似性的计算如式(1)所示:
(1)
其中Γ(i)、Γ(j)分别表示节点i和节点j的邻居,|Γ(i)∩Γ(j)|表示节点i和节点j的共同邻居的数量,|Γ(i)∪Γ(j)|表示节点i和节点j的联合邻居的数量.当节点i和节点j之间的Jaccard值越大,表明这两个节点之间的相似度越大.该相似度不仅考虑了两节点之间的共同邻居,而且还纳入了两节点各自的邻居信息.
为了更好地利用拓扑深层次信息和节点属性信息,基于Jaccard相似度[16]和Sφrenson相似度[17],本文提出联合相似度进行建模使潜在表征更好地辅助特征选择.联合相似度S不仅考虑了节点的邻居信息,而且还考虑了节点的度信息,可以更深入地表达拓扑信息.节点i和j之间的联合相似度Sij如下:
(2)
其中d(i)、d(j)分别表示节点i和节点j的度.如果节点i和j之间没有共同邻居,则联合相似度Sij为0,否则两节点的共同邻居数越多,且联合邻居数和平均度越少,则相似度Sij越大.和Jaccard相似性相比,Sij提升了有共同邻居的节点间的相似度,可以更好地挖掘网络拓扑的深层次信息.
联合相似度S比邻接矩阵A更能挖掘出拓扑结构信息.以节点数为6的网络为例,对应的邻接矩阵A和联合相似度S如图2所示.例如,节点3和其邻居(节点1、节点2、节点4)之间的联合相似度S分别为:1.17、0.53、0.45,显然节点3和
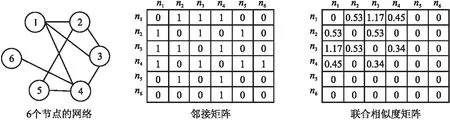
图2 邻接矩阵和联合相似度矩阵示例图Fig.2 Sample diagram of adjacent matrix and joint similarity matrix
节点1的相似度最高,从图2的6个节点的网络中也可以看到节点3与节点1的拓扑结构更为相似.而在邻接矩阵中,节点3和其邻居(节点1、节点2、节点4)的相似性并没有区别.此外,节点2与节点5并没有共同邻居,从S矩阵中可以看到节点2与其邻居(节点1、节点5、节点3)之间的相似度分别为0.53、0、0.53,因此节点2跟节点1、节点3会更加相似,而不是和节点5相似.
为了使潜在嵌入表示向量更好地保持拓扑的性质,对网络拓扑建模,将联合相似度矩阵S分解为矩阵因式,得到拓扑嵌入的目标函数如下:
(3)

为了使潜在表征L更好地辅助特征选择,再以L为约束,通过多元线性回归模型对节点属性信息X进行建模,得到特征选择的目标函数如下:
(4)
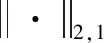
最小化式(4)可以使属性信息矩阵X与转换参数矩阵Z的积逼近潜在表征L,从而可以帮助特征信息学习到更合适的潜在表征,使潜在表征可以更好地指导特征选择.
结合公式(3)和公式(4),得到最终的目标函数如下:
(5)
其中,β是平衡联合相似度拓扑建模和特征选择的参数.
可以采用交替优化算法[5]来求解以公式(5)为目标的优化问题.当L固定时,式(5)是一个凸函数,因此对J(Z,L)求导,当Z趋近于0时,可以得到:
XT(XZ-L)+αDZ=0
(6)
其中,D∈Rm×m是对角矩阵,它的第i个对角元素为:
(7)
其中ε为一个非常小的常数.由此可以得到:
Z=(XTX+αD)-1XTL
(8)
将式(8)代入式(5),可以得到:
(9)
其中M=XTX+αD.式(9)是一个标准的约束优化问题,可以使用投影梯度法进行优化:
(10)
令Ll是L的第l次迭代更新,Ll+1的更新如下:
Ll+1=P[Ll-sl▽J(Ll)]
(11)
其中P[Ll-sl▽J(Ll)]是框投影运算符,用于将点投影到有界区域.
当L固定时,根据公式(8)更新Z,而Z固定时,根据公式(11)更新L,交替进行直到目标函数式(5)收敛,由此得到节点属性的重要性系数,再利用重要性系数对节点属性矩阵X进行筛选就可以得到节点重要属性矩阵F.
3.3 融合共同邻居信息和重要属性信息的表示学习
为了使联合表征向量同时保持网络拓扑和节点属性的相似性,文献[10]对节点拓扑结构和属性信息进行联合建模,得到拓扑建模的目标函数为:
(12)
其中,hi∈Rd、hj∈Rd分别代表节点i和节点j的节点嵌入向量,d为节点嵌入向量的维数.如果节点i和节点j存在连接,则Aij=1,否则Aij=0.
文献[10]只是进行简单利用邻接矩阵,并没有挖掘和融合更深的拓扑信息.考虑到合适的节点相似性指标可以更好地描绘网络拓扑的特性.一般认为两个拥有更多共同邻居的节点比两个共同邻居较少的节点更为相似.因此本文提出融合共同邻居信息的节点相似性指标如下:
(13)
节点相似度SAij为节点i和节点j的相似性.如果节点i与j相连,由式(13)可知,SAij为节点i和节点j的共同邻居数|Γ(i)∩Γ(j)|在总节点数n中的占比.如果节点i和节点j不相连,则SAij为0.
将筛选得到的节点重要属性矩阵F和原拓扑结构组成一个新网络后,可以基于节点相似性对其拓扑信息建模,使节点嵌入向量更好地表征拓扑信息,拓扑建模的目标为最小化式(14):
(14)
重要属性建模是基于属性接近度来构建的,属性接近度可以用来描述两节点之间重要属性的相似程度[19],采用余弦相似度,公式如下:
(15)

进而对节点重要属性信息进行建模,其目标为最小化式(16):
(16)
通过最小化式(16)可以使节点嵌入矩阵H∈Rn×d和HT∈Rd×n的积近似逼近属性接近度矩阵SF∈Rn×n,使得到的节点嵌入向量很好地保持属性接近度.
因此,对融合共同邻居信息的节点相似度矩阵SA∈Rn×n和重要属性接近度矩阵SF联合建模,得到最终的目标函数如下:
(17)
其中λ是拓扑建模与属性建模所占比例的权衡系数,λ越大表示拓扑结构信息考虑得越多.
上述以式(17)为目标函数的优化问题可以重新表述为一个双凸优化问题[10].令Y=H,可以将公式(17)重新表述为一个线性约束问题:
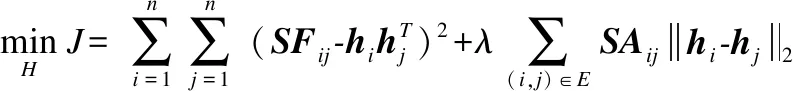
(18)
得到该双凸优化问题的增广拉格朗日函数如下:
(19)
其中增广拉格朗日参数ρ>0,ui为对偶变量,i=1,2,3,…,n.用ADMM算法[10]求解该函数,迭代方法如下:
(20)
(21)
Ul+1=Ul+(Hl+1-Yl+1)
(22)
其中,l为迭代次数.
对式(20)和式(21)求导得到hi和yi的更新公式如下:
(23)
(24)
其中I为单位矩阵.
综上所述,对融合共同邻居信息的节点相似度矩阵SA和重要属性接近度矩阵SF联合建模后,采用ADMM算法[10],根据式(23)和式(24) 分别迭代更新hi和yi,直到目标函数式(17)收敛,就可以得到节点嵌入向量.
3.4 算法步骤和复杂度分析
本文算法分为两个阶段:第1阶段为基于节点联合相似度潜在表征的特征选择,第2阶段为融合邻居信息和重要属性表征学习的社区发现,算法的主要步骤如下:
步骤1.针对属性网络G=(V,E,X)及其邻接矩阵A,设置待选择的重要属性个数t、节点嵌入向量的维数d和参数α、β、λ,并根据式(2)计算节点联合相似度矩阵S;
步骤2.根据式(3)和式(4)分别对基于节点联合相似度S的拓扑结构信息和节点属性信息X进行建模;
步骤3.以公式(5)为目标函数,采用交替优化算法,根据公式(11)和公式(8)交替更新潜在表征L和转换参数矩阵Z;
步骤4.重复步骤3直到目标函数式(5)收敛,得到节点属性的重要程度系数,筛选出前t个重要的节点特征,得到重要属性信息矩阵F;
步骤5.构建新网络G′=(V,E,F),根据式(13)计算融合共同邻居信息的节点相似度,得到节点相似度矩阵SA;
步骤6.根据式(15) 计算重要属性接近度,得到重要属性接近度矩阵SF;
步骤7.对SA和SF联合建模,以式(17)为目标函数,采用ADMM算法,根据式(23)和式(24)分别更新hi和yi;
步骤8.重复步骤7,直到目标函数式(17)收敛,得到节点嵌入向量;
步骤9.运行k-means算法对节点嵌入向量聚类,得到节点类别标签,实现社区划分.
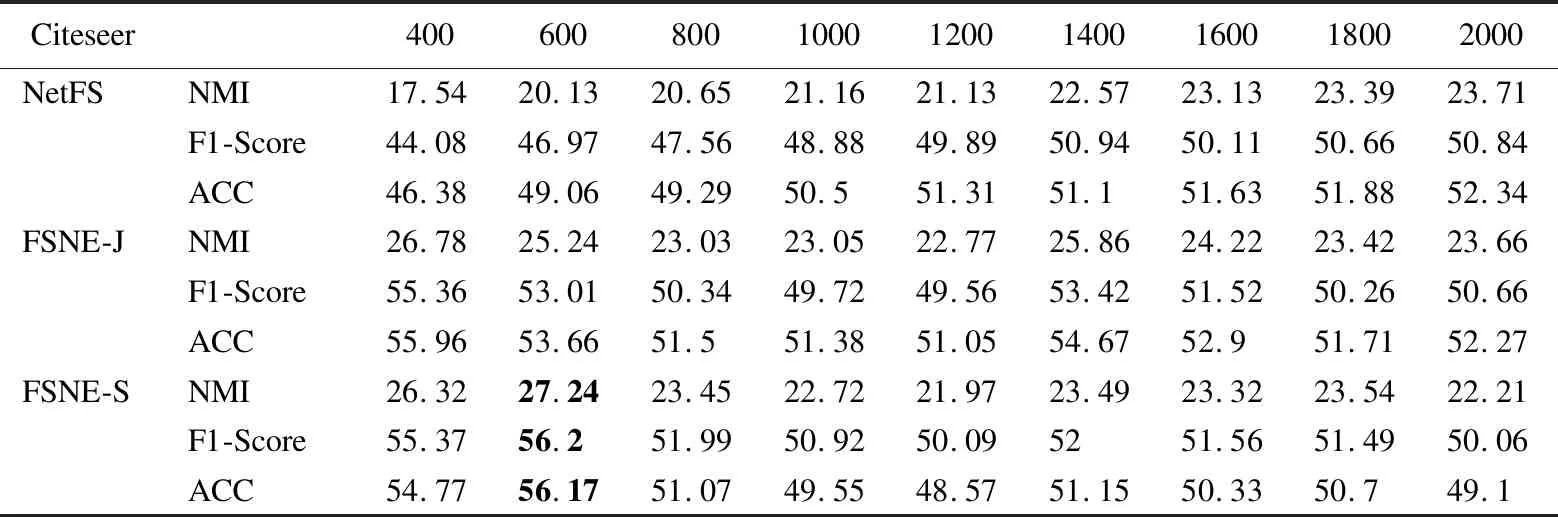
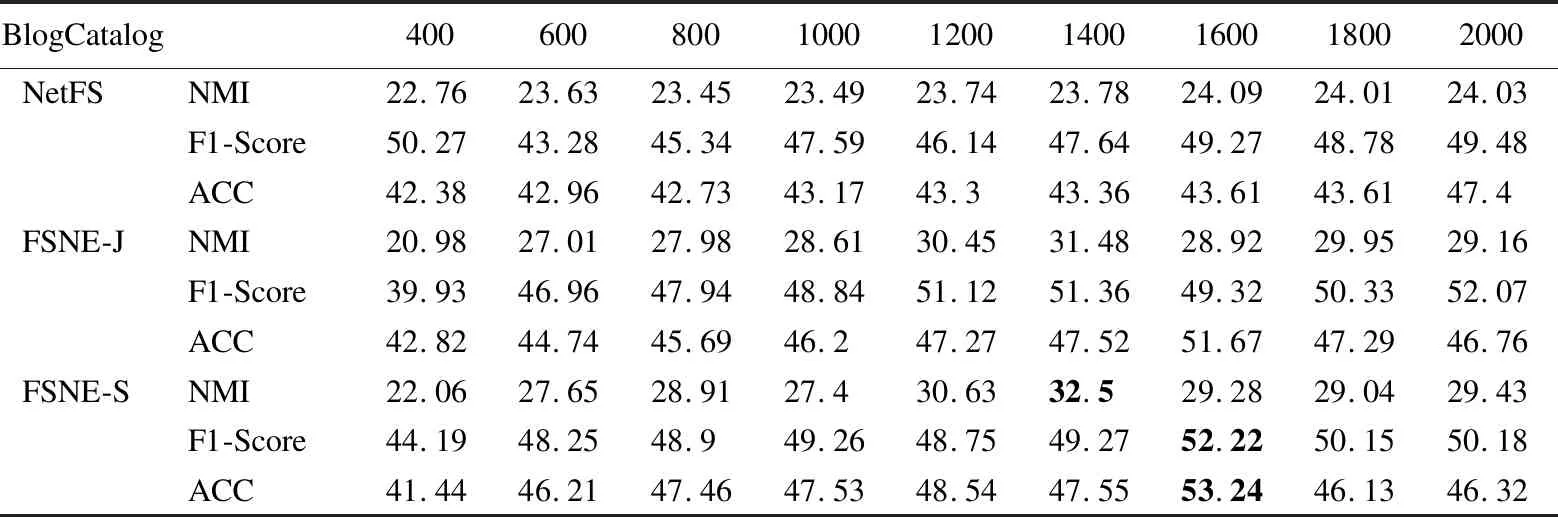
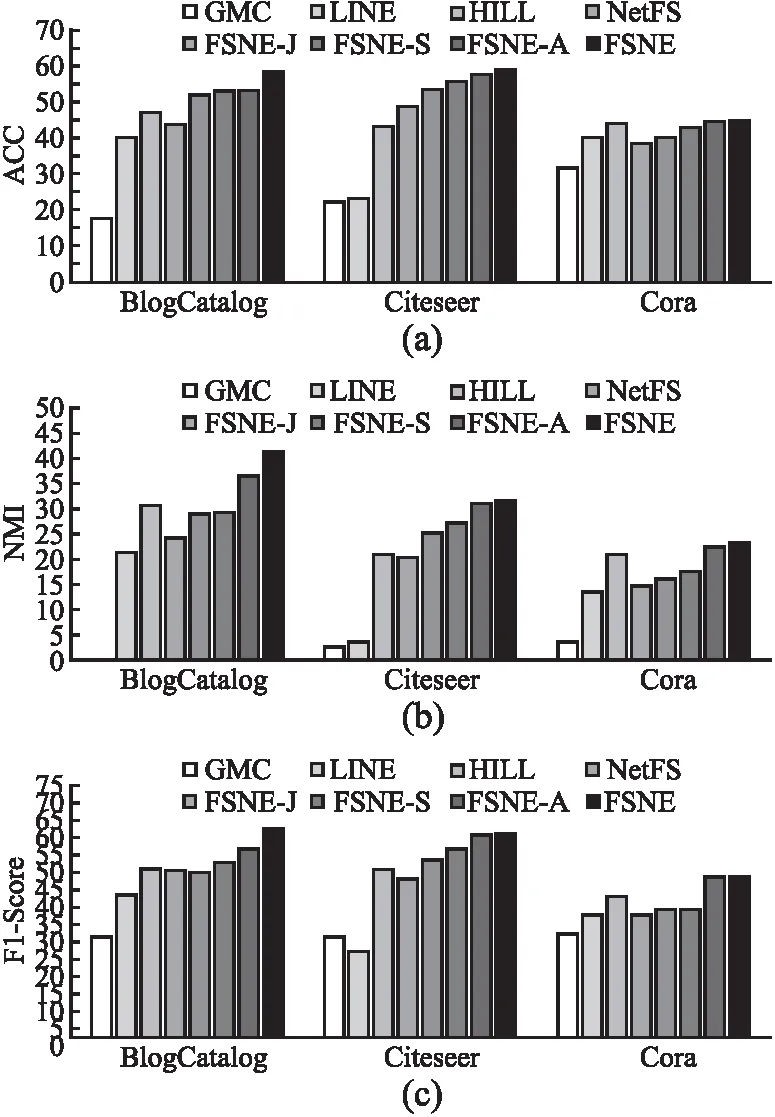
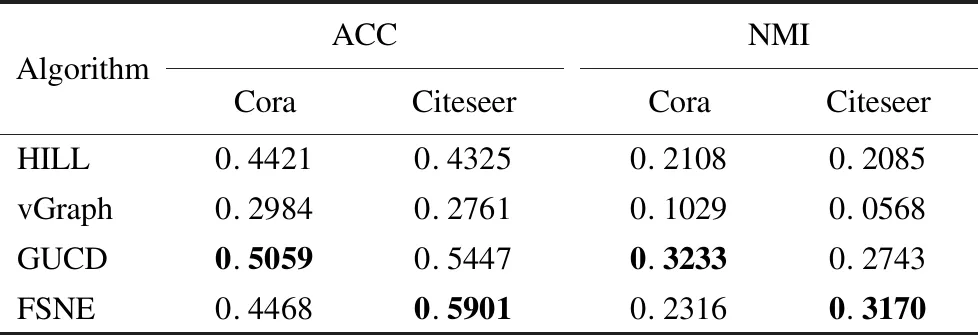
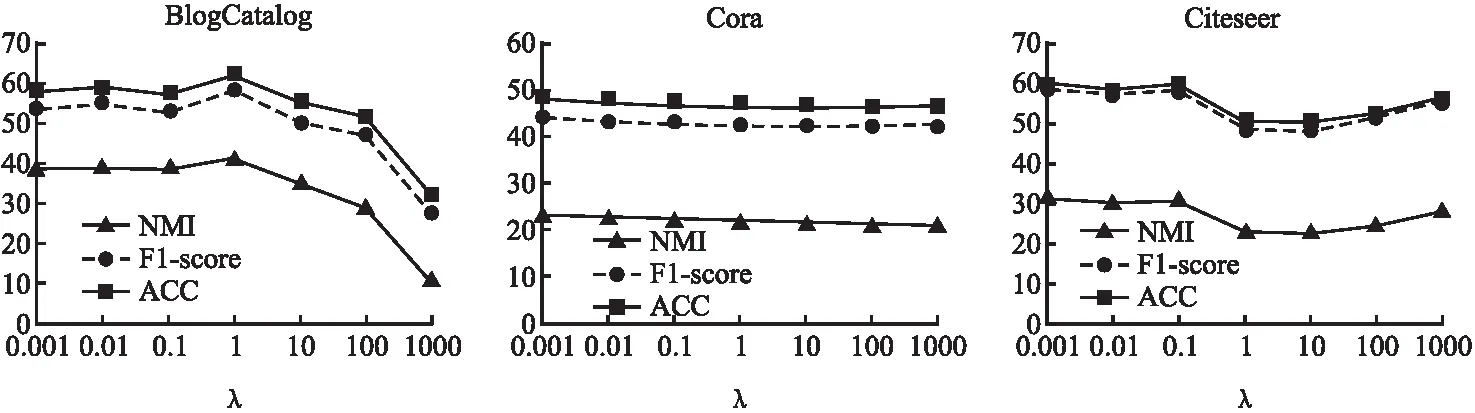
上述步骤1计算联合相似度S的复杂度为O(|E|),|E|为边的数量;步骤2~步骤4,使用交替优化算法更新Z和L,时间复杂度为O(nm2+m3+m2c+ncm),n为总的节点数量,其中节点的属性类别个数m和节点潜在表征向量的维数c都是常数,因此时间复杂度为O(n);步骤5中计算相似度SA的复杂度为O(|E|);步骤6~步骤8的优化求解计算的复杂度为O(nNF+n2/k),NF为F中非零的个数,k为ADMM[10]算法中并行处理器的个数;步骤9中k-means的时间复杂度为O(n).一般情况下,n<|E| 本节使用多个特征选择算法(LapScore[2]、NDFS[3]、LUFS[4]、NetFS[5]和SPEC[6])、网络表示学习算法(LINE算法[9]、HILL算法[10]、GMC[11]、vGraph[12]和GUCD[14])与本文算法在3个真实网络数据集上进行对比分析,所有仿真实验均在装有i9 9900kf CPU和64G运行内存的计算机上完成. 使用3个经典的属性网络真实数据集(社交博客网络BlogCatalog[10]、文献引文网络Citeseer[20]和机器学习论文网络Cora[21])来测试算法的性能,如表1所示,Labels表示属性网络的原始的标签数以及划分的社区数. 使用3个评价指标分析算法的社团划分性能,分别为ACC、F1-Score和NMI.ACC是用来度量社区划分的正确率[22],公式如下: (25) 表1 3个真实网络数据集的基本信息Table 1 Basic information for 3 real networks 其中,gi表示节点i的真实标签,ri表示算法求得的节点i的类别标签,map(ri)为ri在真实标签集合中找到的一个最佳匹配的标签.f(a,b)表示符号函数,若a=b,则f(a,b)=1;否则为0. F1-Score用于衡量真实社团和算法划分的社团之间的一致程度[13],公式如下: (26) 其中,precision为查准率,recall为召回率,定义如下: (27) (28) 其中,TP是把两个相似节点归为同一个社区或簇的个数,FP是把两个不相似的节点归为同一个社区或簇的个数,FN是把两个相似的节点归为不同的社区或者簇的个数[23]. 归一化互信息NMI∈[0,1]用于衡量预测结果和真实结果的差异[24],其值越接近1表示预测结果越好,公式如下: (29) (30) 其中,I(X,Y)表示真实标签集合Y和预测标签集合X之间的互信息度量,H(·)表示熵,p(x,y)是x和y的联合概率分布函数,p(x)、p(y)分别是x和y的边缘概率分布函数. 4.2.1 特征选择性能分析 首先,以BlogCatalog数据集为例,验证FSNE中特征选择性能,其中FSNE-J和FSNE-S分别为基于Jaccard相似性的特征选择和基于联合相似度S的特征选择,通过特征选择筛选得到重要属性后用k-means算法聚类.将FSNE-J、FSNE-S和其他5种特征选择算法,包括LapScore[2]、NDFS[3]、LUFS[4]、NetFS[5]和SPEC[6],在特征的不同维度进行比较,聚类后得到的2个指标(ACC和NMI)的对比如图3所示.算法参数设置如下:NetFS[5]、FSNE-J和FSNE-S的α=10,β=1;LapScore[2]和NDFS[3]的邻居数为5,SPEC[6]和LUFS[4]的参数和原论文相同. 图3显示的是FSNE算法的特征选择部分(FSNE-J、FSNE-S)与其他特征选择算法在各个维度上的对比.图3中,FSNE-J、FSNE-S算法在维度>600的社团划分性能(ACC和NMI值)均高于其他特征选择算法,只有在维度为400时和NetFS算法的性能接近,但还是比其他特征选择算法性能好.而基于联合相似度的特征选择FSNE-S在维度为600~1600时取得的ACC值都超越了基于Jaccard相似性的特征选择FSNE-J的ACC值,而NMI值也仅在1000维时低于FSNE-J.由此可得,FSNE-S取得了比FSNE-J与其他算法更好的性能,在特征选择上有良好的效果. 图3 FSNE-J、FSNE-S与其他特征选择算法在BlogCatalog上的ACC和NMI值比较Fig.3 ACC and NMI value comparison of FSNE-J,FSNE-S and other feature selection algorithms on BlogCatalog 为了进一步验证FSNE中特征选择部分对其他数据集的特征选择性能,在3个真实网络数据集Citeseer、BlogCatalog和Cora上对3个指标(NMI、ACC和F1-Score)进行比较,结果分别如表2~表4所示. 表2~表4显示的是FSNE-S、FSNE-J和NetFS在3个数据集上各维度的比较.在BlogCatalog和Citeseer数据集上,设定维度为[400,600,800,1000,1200,1400,1600,1800,2000].由于Cora数据集上的节点维度最高为1433维,因此设定维度为[400,600,800,1000,1200,1400].表中加粗部分为在各指标中取得的最高值. 在Blogcatalog数据集(见表3)上,FSNE-J取得的NMI值比NetFS高出大约30%.NetFS取得的最高F1-Score值为50.27,此时FSNE-J为52.07,NetFS的ACC值最高为47.4,而FSNE-J可以达到51.67,超过NetFS将近10%.在Cora数据集上,虽然NetFS的NMI值在1000维时取到了最好值,但其他维度均低于FSNE-J,对于F1-Score和ACC值,FSNE-J都取得比NetFS好的效果,分别为39.24和41.21.这是由于,FSNE-J结合节点相似度(Jaccard相似性)来辅助特征选择阶段,而NetFS只是利用简单的网络拓扑,挖掘到的信息不多,综上所述,FSNE-J算法的效果在3个数据集上比NetFS算法都要好.同时从表中可见,FSNE-J取得的NMI值均低于FSNE-S,可以表明基于联合相似度的特征选择FSNE-S取得了良好的效果. 表2 Citeseer上FSNE-J、FSNE-S和NetFS的3个指标对比Table 2 Comparison of FSNE-J、FSNE-S and NetFS in three indicators on the Citeseer 表3 BlogCatalog上FSNE-J、FSNE-S和NetFS的3个指标对比Table 3 Comparison of FSNE-J、FSNE-S and NetFS in three indicators on the BlogCatalog 表4 Cora上FSNE-J、FSNE-S和NetFS的3个指标对比Table 4 Comparison of FSNE-J、FSNE-S and NetFS in three indicators on the Cora 4.2.2 社区划分性能分析 为了验证FSNE算法在社区发现任务上的性能,首先与LINE算法[9]、HILL算法[10]、GMC[11]和NetFS[5]等进行对比,其中FSNE-A是联合节点重要属性F和链接矩阵A嵌入的社区发现方法,它和FSNE算法的特征选择部分相同,但筛选出重要特征后用一般链接矩阵的网络拓扑结构嵌入(见公式(12))进行社区划分.算法参数设置如下:LINE[9]的最小批量大小为128,学习率为0.025,负采样的数量为5;HILL[10]算法中,Blogcatalog数据集的λ=10-0.6,Citeseer数据集和Cora数据集的λ=0.86;FSNE-A和FSNE中,Blogcatalog数据集的λ=1,Citeseer数据集和Cora数据集的λ=0.001;GMC[11]的参数和原论文一样.LINE[9]、HILL[10]、FSNE-A和FSNE的节点嵌入向量维数d=100;NetFS[5]、FSNE-J、FSNE-S、FSNE-A和FSNE中,Blogcatalog数据集的节点特征维数为1600,Citeseer数据集和Cora数据集的节点特征维数为600. 图4 FSNE和其他算法的社团划分性能对比Fig.4 Community partitioning performance comparison of FSNE and other algorithms 图4(a)~图4(c)分别为FSNE算法与其他算法在3个数据集上的ACC、NMI、F1-Score的对比.可以看到,FSNE在3个数据集上的ACC、NMI、F1-Score值高出LINE、GMC、HILL和NetFS算法,这是由于FSNE中的节点联合相似度潜在表征以及融合共同邻居的结构嵌入能更好地深入挖掘网络拓扑方面的信息,但LINE没有考虑节点属性,NetFS没有深入挖掘拓扑结构信息,而GMC、HILL也未较好融合拓扑和属性信息.此外,FSNE-A在3个数据集上的ACC、NMI、F1-Score值都高于HILL算法,因为FSNE-A在HILL算法的基础上融合了节点重要属性信息,而不是节点的所有属性,由此验证了基于节点联合相似度的特征选择是可以进一步提高属性网络表示学习性能的.在3个数据集上的ACC、NMI、F1-Score值,基于节点联合相似度潜在表征的FSNE-S高于基于Jaccard相似性表征的FSNE-J,而FSNE-J又高于NetFS,说明网络拓扑的深层次信息可以更有效地指导特征选择,从而提高社团发现的性能;同时,FSNE高于FSNE-A,而FSNE-A又高于FSNE-S,说明得到节点的重要属性后,把节点重要属性进一步和网络拓扑结构联合嵌入得到节点向量表示,特别是深入挖潜网络拓扑结构,把局部链接(即共同邻居)信息和节点重要属性信息联合嵌入得到节点向量表示可以更好地实现社区划分,图4表明了FSNE在社区划分上的性能优势. 表5 FSNE和HILL、vGraph、GUCD的对比Table 5 FSNE compared with HILL,vGraph and GUCD 为了进一步分析所提FSNE算法的社团划分性能,FSNE算法和HILL、vGraph[12]、GUCD[14]在Cora和Citeseer数据集上进行了比对.vGraph[12]的节点嵌入维数d设置为100,其它参数设置和原文一样.由表5可知,在Citeseer数据集上,FSNE的 ACC值和NMI值是最高的;而Cora数据集上,其ACC值和NMI值位居第2,仅次于GUCD[14],但仍然高于HILL和vGraph[12].因为FSNE算法深入挖掘网络拓扑结构(共同邻居信息)来提高社区检测的性能.由于Cora和Citeseer在构建邻接矩阵时存在边数少于实际边数的情况,其中缺失边率分别为2.8%和1.5%.FSNE算法对Citeseer的求解性能优于Cora,同时也体现了挖掘共同邻居信息的效果. 图5 FSNE在不同参数下的NMI、F1-score和ACC值Fig.5 NMI,F1-score and ACC values of JSNE with different parameters 4.2.3 参数分析 对FSNE算法的参数α、β设置同NetFS,有关α、β的分析见文献[5],这里对FSNE算法的另一个参数λ进行了仿真实验以及分析.图5分别展示了FSNE算法在3个数据集上不同参数λ下的NMI、F1-socre和ACC值,λ分别设置为0.001,0.01,0.1,1,10,100和1000.在BlogCatalog数据集中,FSNE取得的NMI、F1-socre和ACC值曲线的趋势随着参数λ的上升到达最高点后,然后不断下降.在Citeseer数据集中,可以看到最高点在0.001处,而且在Cora数据集中,曲线的变化不大,是由于节点的属性维度本身就较小,因此参数的变化对效果影响不大.因此这3个数据集中λ参数设定如下:BlogCatalog的λ=1,而Citeseer和Cora中λ=0.001. 从属性网络表征学习的角度出发,结合特征选择,本文提出了基于节点联合相似度潜在表征的特征选择,将筛选后得到前t个重要属性,与原拓扑组成新网络,通过基于矩阵分解的属性网络表征学习框架将局部链接拓扑和节点重要属性联合建模得到节点嵌入向量,然后用k-means算法聚类实现社区划分.3个真实网络数据集上的仿真实验验证了本文算法不仅具有良好的特征选择性能,而且具有优良的社区划分算法性能.未来,准备研究动态属性网络嵌入及其与多元信息融合,同时解决特征选择维度的自动确定问题,以便更好地应用于电商网络流量聚合、社交平台兴趣发现和金融领域反诈骗等实际场景.4 实验与结果分析
4.1 数据集及评价指标
4.2 结果对比分析


5 结 论
