终点导向的电动汽车负载均衡充电导航策略
2023-05-12林尔杰韩光洁廖律超
林尔杰,韩光洁,孙 宁,廖律超
1(福建工程学院 福建省汽车电子与电驱动技术重点实验室,福州 350118) 2(福建工程学院 计算机科学与数学学院,福州 350118) 3(福建工程学院 交通运输学院,福州 350118) 4(河海大学 物联网工程学院,江苏 常州 213022)
1 引 言
为应对日趋严重化的环境污染和资源短缺等问题,世界多国陆续发布了关于燃油车的禁售时间表[1],推行节能减排政策把发展方向转向了新能源汽车.截至2021年6月,我国新能源汽车增量持续呈高速增长态势,并实现了连续4年突破百万,目前保有量已高达603万辆.电动汽车(Electric Vehicle,EV)的发展需求带来了城市充电站[2]等配套设施要求,充电站需要更加均衡分配充电需求车辆.然而,当前的充电配套设施发展滞后且配置不合理,加之EV的行驶里程焦虑问题[3],按照传统汽车导航或者盲目就近选择充电,容易产生个别充电站严重扎堆充电现象,导致部分充电站使用率低下或者排队等待时间过长问题,难以满足充电设施和电动汽车充电需求的快速变化,急需对可均衡分配充电需求的充电导航策略进行研究,以解决电动汽车的发展阻力.
充电设施资源的不合理分配[4]和充电行为的随机性,容易造成局部充电拥堵,严重影响电网安全稳定性[5]、城市交通运行效率[6]以及充电设施的维修成本.随着充电方式的更新发展,快速充电技术和换电技术[7]以高效的优势获得大多数EV用户的认可.快速充电技术可在半小时内能使EV的电池荷电状态(State of Charge ,SOC)从20%上升到80%[8],而换电技术则因为高昂的成本,并未得到普及应用.在充电站建设滞后于用户充电需求的前提下,如何在现有充电设施基础上,使用信息化手段更加均衡地引导EV用户进行充电选择,以发挥城市充电资源最大利用率,是本文研究面临的挑战性问题.
目前,很多学者针对EV用户最小期望成本心理,采取价格激励策略以指导EV充电选择.文献[9]以最小化总配送成本,提出了一个电动汽车最佳行驶路径模型,并分别考虑定期充电和快速充电两种方式的分时电价.文献[10]考虑用户对于价格的敏感度,设计一个最优定价方案协调充电选择,降低充电站的服务下降率.文献[11]将充电时长引入充电价格模型,通过价格激励用户调整充电时长,以达到降低充电等待时长的目的.上述研究均是对充电价格的静态调整,即同一区域内充电站在不同时段采取一样的分时定价,这种方法会导致各充电站利用率严重不均衡.若将各充电站充电价格与动态排队情况结合[12],动态制定充电价格,既能满足用户对于充电价格和等待时间的共同期望,也能较好地调度充电负荷平衡[13].
近期很多研究也综合考虑了多种因素对充电选择的影响.文献[14]根据行驶距离、充电费用和等待时间最小化综合充电成本选择充电站进行充电.文献[15]通过充电站、电力控制中心和智能交通系统中心组成多模块信息反馈,以行驶时间、等待时间和充电时间总和最小化选择目标充电站.文献[16]考虑行驶里程的限制,建立用户的预约分配模型,以获取最大化经济利益.文献[17]考虑电网和交通环境约束,基于充电成本和时间最小化构建充电导航模型.上述研究中充电选择均只考虑了EV到充电站的充电成本,未考虑EV充电结束后的路径规划,可能会增加EV的绕行距离和时间成本.
价格激励策略只能对EV进行粗略的引导,导航系统则可结合交通信息将EV有序引导至各充电站.文献[18]考虑交通和电网运行信息的情况下,提出了一个智能交通系统框架来实现最优的充电导航策略,通过充电功率调节方案来降低对电网的影响,并使用充电价格调整方案来均衡充电负荷.文献[19]提出一个综合考虑交通和电力系统的实施导航框架,应用粒子群优化算法寻找充电站间博弈的最佳策略.文献[20]考虑极端天气影响,提出一种动态交通/天气模型的分层导航策略,以时间选择层与路径选择层分别为用户寻找最佳充电时间和路径选择.
基于以上研究,本文提出了一种基于价格激励的快速充电预约导航策略.首先,本文提出了一种多网络协作模式的充电导航系统框架,并通过蒙特卡洛方法模拟获得充电需求时空分布.其次,为了提高各充电站利用率和EV的充电效率,本文提出了一种基于排队率的动态服务费定价模型,实现排队与定价的动态响应,使充电负荷能够在所有充电站之间实现均衡分配.最后,本文也考虑了EV充电结束以后继续前往目的地的路径规划,通过构造充电决策函数,有效减少绕行距离和行驶时间,提高EV用户充电满意度.本文基于某市电动车辆交通数据,为仿真合理设置参数和对比实验,通过实验结果对比验证,证实了本文所提策略的有效性.
本文主要贡献如下:
1)提出了一个交通信息网络、电力网络和充电站网络协同工作模式的充电导航系统框架,协调充电导航策略的信息交互行为,通过预约充电方式为EV用户提供最优充电策略.
2)提出一种基于排队率的动态服务费定价模型,各充电站根据排队率情况,对服务费进行动态调节,实现上调分流和下调吸引的效果,使充电负荷均衡分配至各充电站.
3)构造考虑EV最终目的地的充电决策函数,考虑EV用户充电结束继续前往目的地的路径规划需求,减少绕行距离,提高EV用户充电满意度.
2 协同模式的充电导航框架
本文首先提出一个融合了交通信息网络、电力网络和充电站网络协同工作模式的充电导航系统框架,如图1所示.该充电导航系统主要由EV、充电站组成,与交通信息系统、电力系统通过无线网络进行信息交互,通过云端计算,进行充电决策计算,最终为系统所有EV用户提供全局优化的充电导航结果.该充电导航系统的运行步骤如下:
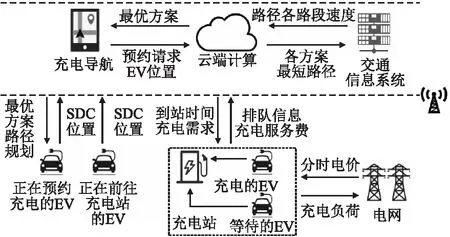
图1 充电导航系统框架Fig.1 Charging navigation system framework
Step1.当EV的SOC状态低至阈值时,EV用户通过充电导航系统发出预约充电请求;
Step2.充电导航系统响应并获取EV的位置和SOC,并将信息传送给云端;
Step3.云端计算EV所有可到达充电站路径方案,并估算各方案到达充电站的时间和充电需求,所有路径方案传送给交通信息系统,到站时间和充电需求传送给充电站;
Step4.交通信息系统根据路径方案将路径所包含各路段的当前速度信息传送给云端;
Step5.充电站结合预约充电EV估算排队情况并根据服务费定价模型估算充电单价,并将信息返回给云端;
Step6.云端结合接收的多项信息,估算所有可行方案,并将最优决策方案传送给充电导航系统;
Step7.EV根据最优方案路径规划前往目的充电站进行充电.
为了减少充电导航系统的复杂,本文假设了以下条件:
1)假设EV均以车辆SOC状态低至设定阈值为产生需求时刻,通过导航系统进行充电的预约决策,结束充电后立即离开充电站.
2)假设充电站之间无恶意竞争,全部接受系统调度策略.
3)假设网络通信和云端计算的延迟时间可以忽略.
3 充电需求预测模型
3.1 路网拓扑图
本文依据图理论形式将复杂的交通路网连接简化为拓扑结构,并以G(N,R)表示路网连接的拓扑关系.其中集合N表示所有路口节点,集合R表示两个路口节点之间的道路路段集合,路网连接拓扑关系矩阵构建如式(1)所示:
(1)
其中i和j分别表示两个路口节点,li,j表示可连通状态下两个节点之间的路段.
3.2 OD矩阵
OD(Origin-Destination)矩阵是起点-终点矩阵,矩阵的行列分别表示所有起点与终点,矩阵元素则表示对应起点与终点的车辆出行量,通常用于城市交通仿真.OD矩阵可通过道路流量观测值运用反推技术获得.本文采用的是非平衡OD反推模型,反推公式如式(2)所示:
(2)
其中,Pi,j_a表示该车辆节点i行驶至j,且途径路段a的概率.为减少复杂工作量,本文采用非平衡OD反推模型以获取出行分布,设Pi,j_a为常数.假设车辆均采用Dijkstra算法进行路径选择,若途径路段a则取Pi,j_a为1,反之则取为0;Qa表示路段a的实际车流量;n表示交通节点数,m表示区域路段数,Ti,j表示待求OD矩阵中的元素.
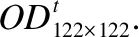
(3)
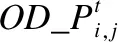
3.3 路段速度矩阵
城市各个路段的道路状况差异和不同时段的车流量变化,会直接影响到各路段的行驶速度,进而导致相同路段在各时段的行驶速度差异.尤其在拥堵的早晚高峰期,城市各路段的行驶速度差异更是明显.本文拟采用类似OD矩阵构建方式,对各路段进行所有时段的行驶速度研究.通过对车辆的轨迹数据处理,提取每个轨迹点的所在位置及其节点i与j节点构成的路段r.根据车辆通行路段r所用时间T与路段长度Lr,计算车辆在各路段的速度v,对研究区域的进行分时段行驶速度分析,如式(4)所示:
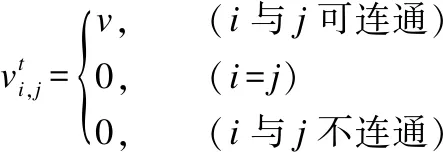
(4)
其中,v表示在t时段时,车辆通行节点i与j相连通道路r的平均速度.
3.4 能量消耗模型
交通状况是决定EV单位里程能量消耗的主要因素,即EV在不同交通状况下的行驶速度v会产生不同的能量消耗.依据城市道路划分等级,研究区域包括4个道路等级:快速路、主干路、次干路和支路,并且各等级依据不同交通状况会呈现不同的平均速度.根据文献[21],EV在不同等级道路的单位里程能量消耗如式(5)所示:
(5)
其中,ΔEks、ΔEzg、ΔEcg、ΔEz分别表示电动汽车在4个等级道路的单位里程能量消耗.当车辆行驶通过路段r,电池消耗如式(6)所示:
Er=Lr×ΔE
(6)
其中,Lr表示路段r的实际长度,ΔE表示单位千米的消耗容量(kWh/km),根据不同城市道路等级确定.
3.5 充电需求时空分布
关于交通模型时空预测的方法有很多[22],本文基于真实的车辆轨迹数据,获取OD出行概率分布,并采用蒙特卡洛方法对EV一天的出行进行模拟仿真,以获取EV的充电需求时空分布,具体过程如算法1所示.首先初始化,随机生成车辆的出发时刻Tcur、地点Pcur和电量SOCcur.然后根据Tcur的OD概率矩阵,随机生成目的地Pdest.假设用户均考虑路径最短,以Dijkstra算法确定路径集合path.路段长度Lr可根据路网连接拓扑关系矩阵获得,路段行驶平均速度可根据路段速度矩阵获得,则t时段内,车辆通过路段r的行驶时间如式(7)所示:
(7)
算法1.需求时空分布仿真算法
输入:车辆数目N、充电阈值SOCd、出发时间分布、出发点地点分布和OD出行概率矩阵
输出:所有充电需求demand
1.初始化:demand_num=0;
2.whilen 3.生成电动汽车的出行时刻Tcur、出发地点Pcur和电量SOCcur; 4.repeat 5. 根据时刻Tcur对应的OD出行概率矩阵,随机生成目的地Pdest; 6. 通过Dijkstra算法确定最短路径集合paths; 7.foreach path in pathsdo#车辆通过路径集合的每一路段 8. 通过式(6)计算电池消耗容量SOCr; 9. 通过式(7)计算路段r的行驶时间Tr; 10. Tcur=Tcur+Tr; 11. Pcur= Pr; 12. SOCcur= SOCcur-SOCr; 13.ifSOCcur< SOCdthen 14. demand_num += 1; 15.returndemand; #充电需求的时间和地点 16.endfor 17.untildemand_num=n 18. n+=1; 19.endwhile EV根据最短路径前往目的地,若中途EV的SOC状态低至SOCd阈值,则输出充电需求的时刻和位置;否则当EV到达目的地时,将继续以该地为新出发地,再次根据OD出行概率矩阵随机生成下一目的地,依次循环模拟所有EV一天中的出行轨迹,最终获得一天24小时的充电需求时空分布. 考虑电网安全性,电网企业通过补贴形式[23],促使充电站运营商调整充电电价吸引EV用户错峰充电,以此减少高峰对电网的冲击.本文通过蒙特卡洛仿真获得的充电需求时间分布,可以简单得到该市日充电低谷和高峰时段,依据充电分时电价标准[24],假设该市充电的分时电价如表1所示. 目前对于充电定价的研究,大多停留在静态策略,即只考虑同一研究区域不同时段的分时定价,虽可以在一定程度上达到调峰的效果,但各充电站利用率仍严重不均衡.区域内的各充电站在同一时段充电单价统一,用户一般会根据到站行驶距离选择最近的充电站,这便导致了部分充电站严重拥堵,而部分充电站利用率低下.基于此,本文提出了一种基于排队率的动态服务费定价模型,如式(8)所示: (8) 其中,λ=Q/U,λ表示充电站的排队率,Q表示站内的实际排队长度,U表示充电站充电桩数目;ζ表示常数系数,PBS表示基本服务费. 所以,充电站充电单价为,如式(9)所示: PC=PE+PS (9) 其中,PE表示电价费用,PS表示服务费用. 当EV前往目的地的途中,SOC低至设定阈值产生充电需求后,暂时停止前往目的地并中途选择充电站进行充电.充电导航系统在剩余里程和排队长度容限的约束下,估算所有可达充电站方案,假设EV均选择最优方案.充电策略决策函数如式(10)所示: minW=C+α×T (10) 其中,C表示充电费用成本;T表示耗费时间,α表示时间成本系数;TW,C表示等待时间,TW,nearest表示距离目标充电站与目的地距离之和最短的充电站的等待时间,γ表示等待时间约束系数. 4.2.1 充电成本 计算公式如式(11)所示: C=TC×PC (11) 其中,TC表示电动汽车充电所需时长,PC表示充电站充电单价. 4.2.2 耗费时间 考虑到用户充电结束后,仍继续前往未到达的目的地.本文分段考虑行驶时间,既考虑产生充电需求点到充电站行驶时间,又考虑充电结束后从充电站继续前往目的地的行驶时间.这样能够有效减少不必要的绕行,提高用户充电满意度.因此总耗费时间包括4个部分,如式(12)所示: T=TWj+TCj+TDj_C+TDj_D (12) 其中,TWj表示车辆等待时间;TCj表示充电所需时间;TDj_C表示前往充电的行驶时间;TDj_D表示充电结束继续前往目的地的行驶时间. 考虑电池的使用寿命,假设车辆每次充电达到电池容量的90%[25],则结束充电.所以车辆充电所需容量如式(13)所示: ECj=90%×Q-ERj (13) 其中,Q表示电动汽车电池容量,ERj表示车辆到站时剩余容量. 则充电所需充电时间如式(14)所示: (14) 其中,P表示充电机功率,η表示充电机充电效率. 以离散集合形式统计每辆EV到达充电站时刻和充电离开充电站时刻,并分别采用降序排序如:到达时刻集合TA={TA1,TA2,…,TAQ,…},离开时刻集合TL={TL1,TL2,…,TLQ,…}.则第Q辆EV到达充电站所需等待时间如式(15)所示: (15) 其中,Q表示到达充电站的第Q辆EV,U表示充电站充电桩数目. 产生充电需求中途前往充电的行驶时间如式(16)所示: (16) 完成充电继续前往目的地的行驶时间如式(17)所示: (17) 本文通过Python3.7平台,利用交通轨迹数据和市中心交通网络对用户充电需求和导航进行模拟仿真,合理设置仿真参数和对比实验,证实了所提充电导航策略的有效性.本文仿真区域占地约200平方公里,以福州市市区的主干道为基础,对主要交通流量的道路进行提取,以道路的交叉口为节点,构建122个节点,212个路段.依据图理论形式将交通路网简化为拓扑连接图,并构建路网连接拓扑关系矩阵,如表2所示.本文实验数据来源于福建省北斗导航与智慧交通协同创新中心,通过ODB设备采集3900辆出租车7天的交通轨迹数据.本文依据文献[26],并进一步考虑充电便利性等因素假设快速充电站的分布情况,如图2所示,共设置14个快速充电站,分别位于各路网节点.仿真设置如下: 表2 路网连接拓扑关系矩阵Table 2 Road network connection topology relation matrix 图2 路网及充电站分布Fig.2 Distribution of road network and charging stations 1)选择BYD E6车型为研究仿真车型,共计3900辆EV,电池容量为60kWh[27]. 2)假设在EV初始状态,SOC服从正态分布NSOC(0.8,0.12)[28].考虑EV的行驶里程焦虑,设置SOC充电阈值为0.2. 3)各快速充电站对应充电容量、充电机功率[29]以及充电效率[30]等参数设置如表3所示. 表3 各充电站配置Table 3 Configuration of each charging station 4)取模型参数值.时间成本系数α:50Yuan/h;常数系数:0.5;充电等待时长约束系数γ:1.5;基本服务费PBS:0.7Yuan/kWh[31]. 通过OD概率矩阵对电动汽车一天的模拟仿真,可以得到充电需求时间分布,如图3所示.仿真产生了两次充电高峰期,分别是早班的1:00~3:00和晚班的15:00~17:00两个时段,单个小时最高充电需求数目接近500辆次.如图4所示,阴影从浅到深依次表示充电需求数目从小到大. 图3 充电需求时间分布Fig.3 Charging demand time distribution 图4 充电需求空间分布Fig.4 Spatial distribution of charging demand 可见充电需求的空间分布相对分散且不均衡,大多分布在研究区域的边围,而且集中分布在各充电站附近,有利于EV寻找充电站补充电能. 为验证本文所提出充电导航策略的有效性,设置了两种不同的充电策略进行对比.策略1:所有EV采用无导航就近策略选择充电[32];策略2:所有EV采用未考虑目的地的充电导航[33],根据综合成本选择最优的充电站进行充电;策略3:即本文推荐方法,所有EV采用考虑目的地的充电导航,根据综合成本选择最优的充电站进行充电. 根据表4和表5所示,对一天内所有充电站的充电车辆数目和平均等待时长进行分析.策略1下分别有416辆、381辆EV集中选择CS 3和CS 7,仅有112辆EV选择CS 14,结果表明就近选择充电会严重导致分配不均衡和平均等待时长的增加;策略2、策略3下各充电站的EV分配数目近似,与各充电站的充电容量基本呈正相关,如最大充电容量的CS 6的EV选择数目最大,而最小充电容量的CS 8的EV选择数目则趋于最小,结果表明充电导航能使EV分配均衡,提高充电站利用率. 表4 日高峰和全日的充电车辆分布Table 4 Distribution of charging vehicles during peak hours and throughout the day 表5 日高峰和全日的充电平均等待时长Table 5 Average waiting time of daily peak and full day charging 根据表4和表5对一天的充电高峰时段进行分析,策略1下选择CS 8的EV数目近似平均值,但因为CS 8充电容量最小,从而导致CS 8的平均排队时间增加;而策略2、3考虑CS 8的充电容量最小,降低了CS 8分配的EV数目,从而提高EV的整体充电效率.这说明了充电导航能使EV更为均衡地分配,降低EV的充电等待时长.通过以上分析可知,EV采取无导航就近选择策略,CS 3、CS 7和CS 8会面临很大的充电压力,而CS 14则利用率低下.相反在充电导航的有向引导下,能够很好缓解CS 3、CS 7和CS 8可能会引起的拥堵,有效提高CS 14的利用率. 图5 充电车辆动态队列Fig.5 Dynamic queue of charging vehicles 图6 充电单价变化情况Fig.6 Change of charging unit price 从服务费定价模型可以看出,各充电站的充电单价与各自容量和EV排队长度有关,因此不同的策略下充电单价的变化也不同.3种策略下各充电站一天的充电单价变化曲线如图6所示.可以明显观察到,策略1下各充电站的充电单价峰值有较大差异,最大充电单价高至4.6Yuan/kWh.策略2、策略3下各充电站都有相近的趋势变化,在高峰时段分别达到峰值,侧面表明了在充电导航下各充电站利用均衡. 图7 某EV充电选择及路径Fig.7 Charging choice and path of an EV 图7显示某辆EV在前往最终目的地(路网节点61)的途中(路网节点34)产生充电需求时,3种策略下的不同充电站选择以及行驶路径.虚线路段表示策略2、策略3下分别前往CS 5进行充电的路径和充电结束后前往最终目的地的路径;粗实线路段表示策略3下分别前往CS 7进行充电的路径和充电结束后前往最终目的地的路径.3种策略下的充电站选择对应的各成本情况如表6所示,可见策略1和策略2选择CS 5进行充电,最后前往最终目的地会产生不必要的绕路,而策略3则选择离最终目的地较近的CS 7进行充电,减少了一定的时间成本和车辆损耗. 表6 某EV充电选择详情Table 6 Charging selection details of an EV 本文为了提高EV用户满意度和实现充电负荷的均衡分配,提出了一种基于价格激励的EV充电预约导航策略.首先结合动态排队率,构建充电服务费定价模型.然后构造考虑最终目的地的充电决策函数,使充电选择更加靠近目的地,有效减少EV的绕行成本.仿真结果表明,采用本文提出的充电导航策略,可以使充电负荷均衡分配,提高快速充电站的利用率,缓解充电压力和排队问题. 本文研究主要针对单辆EV的充电选择策略.面对多车辆同时选择相同充电站,可能造成部分EV估算的充电费用和排队时间与实际有较大偏差,致使预约充电产生不公平性,后续工作将继续对此进行研究.4 充电导航决策
4.1 动态定价模型
4.2 目标函数
s.t.ER/ΔE≥LDj_C
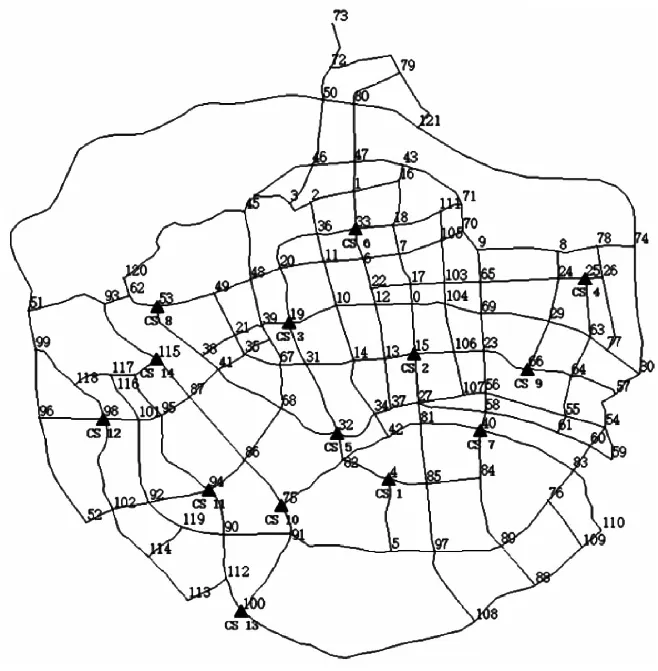
TW,C<γ×TW,nearest5 仿真实验
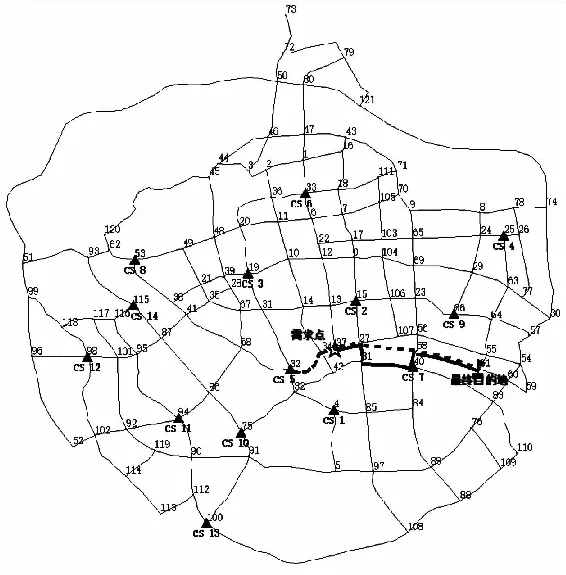
5.1 仿真设置


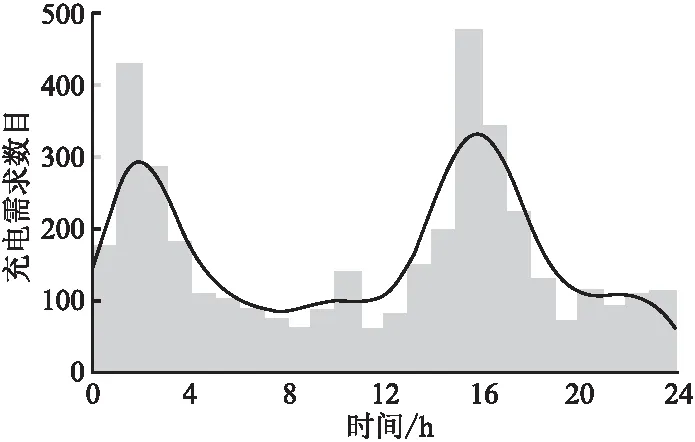
5.2 仿真结果分析



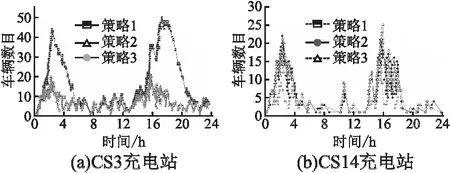

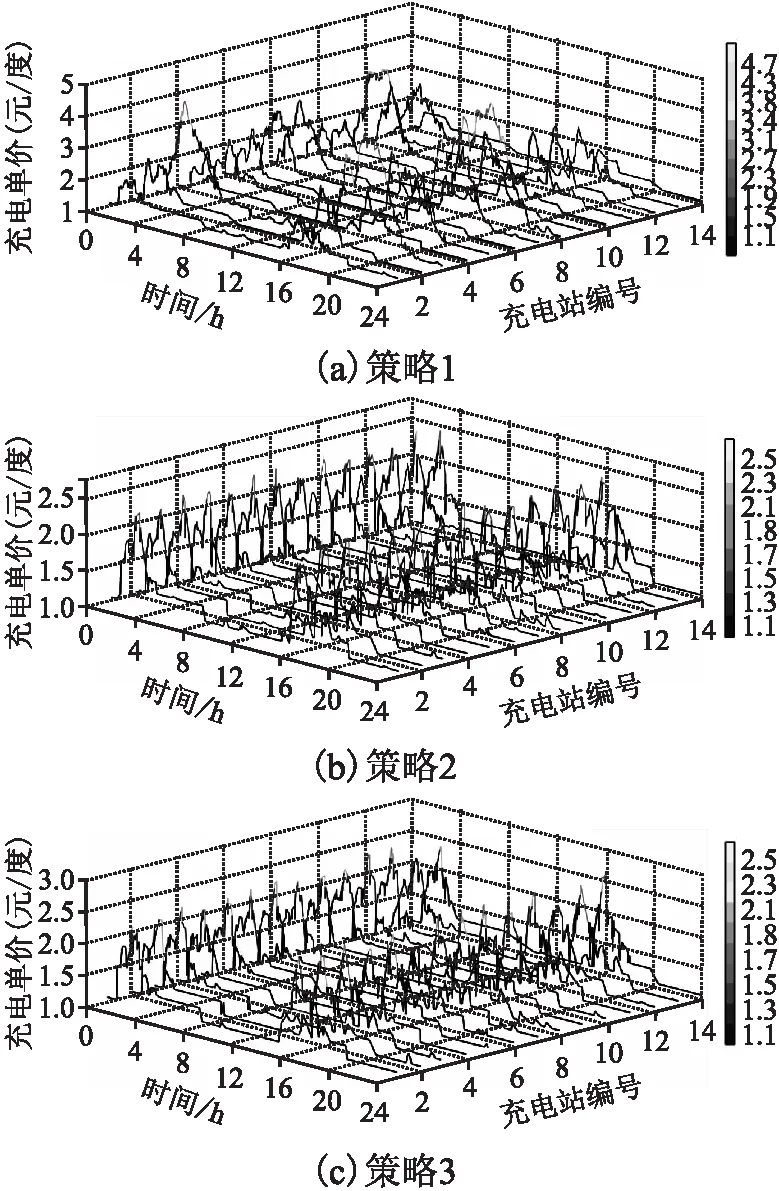

6 结 语
