基于气体扩散方程的分子污染仿真与污染效应试验研究

2023-05-12宫向华郭志昌吴晓宏

航天器环境工程 2023年2期

宫向华，周岩，李杨，李佳，郭志昌，吴晓宏*

（1.哈尔滨工业大学化工与化学学院；2.哈尔滨工业大学数学学院：哈尔滨 150001）

0 引言

随着航天器向高性能、高可靠性及长寿命方向发展，分子污染对航天器上光学系统、热控装置、太阳电池及电子器件等的影响越来越受到重视[1-2]。航天器广泛使用的环氧基碳纤维复合材料（carbon fiber reinforced plastic, CFRP）、热控涂层、环氧胶及硅橡胶等非金属材料会在空间环境作用下缓慢放气，产生小分子碳氢类、邻苯二甲酸酯类及硅氧烷等有机分子污染物[3-5]，并沉积于航天器敏感部件表面，可导致航天器性能下降，甚至造成载荷失效。因此，航天器非金属材料空间分子污染控制已成为高性能航天载荷研制中亟待解决的关键问题[6-8]。

污染仿真分析是空间分子污染控制的重要环节。近年来，国内外开展了一系列围绕污染产生、传输与沉积评估方法的研究。例如，NASA 开发了NASAN 污染分析软件，用于国际空间站的污染分析与评估[9]，并在1996 年发射了MSX 中期试验卫星，专门对卫星敏感系统的分子污染效应进行飞行实测，获得了航天器在轨污染的沉积量数据[10]；通过实测与仿真数据的对比发现，两者良好的数据吻合性证明了污染仿真可以用于航天器整星或载荷的分子污染评估，进而指导航天器设计与载荷性能优化。国内对污染仿真评估的研究起步较晚，模块化仿真软件的开发和测试也不够系统。现有研究工作主要是基于Monte Carlo 方法对简单结构进行污染模拟预估，但难以进行大尺寸复杂结构的系统级污染预估计算，而且污染分析结果相关的地面试验数据或在轨试验数据的验证较少[11-12]。

Monte Carlo 方法是最常用的分子污染仿真分析手段，主要利用射线追踪的方式对分子从放气源表面出射，在航天器周围运动、碰撞，在敏感表面沉积等过程进行模拟仿真[13-14]。但由于载荷结构通常比较复杂，Monte Carlo 方法计算耗时长，可能带来昂贵的设计成本，因此有必要研究新的仿真分析方法，实现精准快速的仿真分析。

本文以某空间相机光学系统为研究对象，提出利用扩散方程创新性地构建能够准确描述放气分子扩散及沉积过程的偏微分方程模型，利用高精度偏微分方程数值解法进行模拟仿真，获得放气污染分子沉积的定量分析结果，并结合地面试验对污染效应进行研究。

1 典型光学载荷结构及其污染特性分析

1.1 典型光学载荷结构

本文所研究的光学载荷所采用的是卡塞格林反射式物镜系统，相机结构及尺寸如图1 所示，结构中包括4 个敏感面——杜瓦窗口、主镜、次镜和扫描镜，污染物分子在敏感面上的沉积将会极大影响系统成像质量，是污染物仿真分析与试验研究的关键表面。

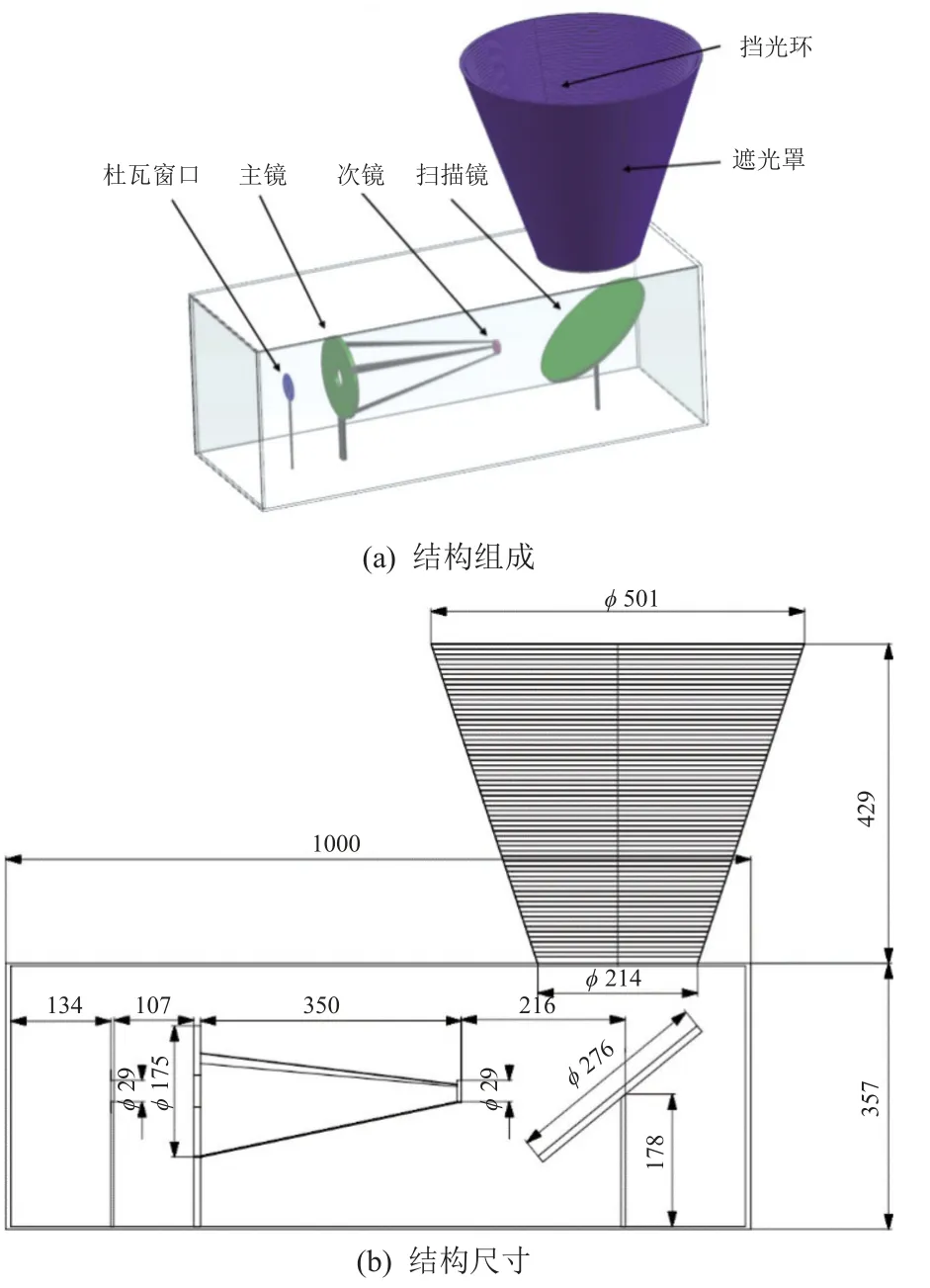
图1 某空间相机光学系统结构示意Fig.1 Schematic diagram of optical system structure of a space camera

1.2 材料的污染物放气特性

材料的放气过程包括解吸、扩散和解离3 种过程，这3 种过程除了与放气时间有不同的对应关系，还与材料的活化能（Ea）和温度（T）密切相关，如表1 所示。其中活化能是指分子从常态转变为活跃状态所需要的能量。由表1 可知：解吸过程所需的活化能相对很小，持续的时间较短，且通常只发生在污染物表面，对在轨航天器的污染贡献相对较小；虽然解离与时间无关，但需要很高的活化能并且活化对应温度也很高，在航天器实际在轨工作过程中发生的概率很低，因此，解离过程不是空间分子污染的主要来源；与解离过程相比，扩散过程具有中等活化能和活化对应温度且过程发生所需的时间较长，因此成为在轨航天器材料污染分子放气的主要过程和关键机制[15-16]。

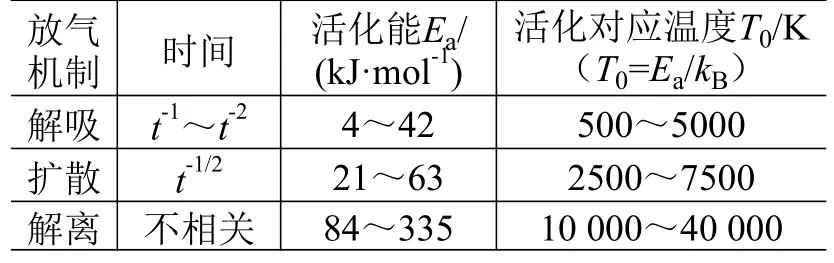
表1 材料放气过程的典型数据[17]Table 1 Typical data of material outgassing process[17]

由扩散过程导致的材料质量损失量可表示为[17]

式中：C为需通过试验确定的气体常数；m为产生污染分子的材料的质量，g；T0为活化对应温度（T0=Ea/kB），K；Ea为材料的活化能，J；kB为Boltzmann常数，kB=1.380 649×10-23J/K；T为热力学温度，K；t为时间，h。

对式(1)进行积分，所得到的积分式给出了t1～t2时间段内释放出的气体质量∆m的表达式

由材料放气速率的定义（单位面积下单位时间内释放出的气体质量）可知，

式中：v为放气材料的放气速率，(g·m-2·h-1)；ρs为放气材料的面密度，(g·m-2)。将式(2)代入式(3)，当t1=0 时可得：

式(4)描述的是放气速率与放气时间和放气材料温度的关系，因此，需要先通过相关试验来获得材料的气体常数C和活化能Ea，再将已知的放气材料面密度ρs、温度T以及放气时间Δt代入式(4)，便可求出材料的放气速率。根据式(2)可知，在固定放气时间内且在两个不同放气温度条件下，分别测定放气材料的初始质量和最终质量，计算质量变化Δm便可获得该材料的C和Ea值。

本文中光学相机采用环氧基CFRP 作为箱体结构材料，依据国家航天行业标准QJ 1558B—2016《真空条件下材料挥发性能测试方法》对环氧基CFRP 进行放气测试，结果得到其真空条件下的放气总质量损失（TML）在373.15 K 和398.15 K 下分别为0.050%和0.097%；据此可由式(2)计算出环氧基CFRP 的气体常数C为1.954；活化能Ea为5.436×10-20J；活化对应温度为3 937.279 K。那么，已知环氧基CFRP 的面密度ρs为1.648×103g·m-2，根据式(4)计算其单位面积放气速率为

1.3 污染物黏附特性

当气体污染分子与接触面碰撞时，可以黏附在接触面上，也可以被反射出去，其黏附的质量与总入射质量的比值称为黏附系数。现有黏附理论表明，污染分子撞击敏感表面会黏附在其上并建立热平衡，直到获得足够的能量才能克服分子间作用力并逃离表面[18-20]。因此，污染分子在敏感表面上的停留时间主要与敏感面的温度有关。光学相机镜头是成像的关键敏感表面，相应温度条件下分子污染物在镜头表面的黏附系数是影响污染物沉积的关键因素之一。

根据现有航天器分子污染物分析，邻苯二甲酸酯类物质是空间典型分子污染物之一，主要来自环氧树脂、聚氨酯类电缆、复合材料和黏结剂等[21-22]，对光学系统影响极大。本文中光学载荷的环氧基CFRP 箱体结构材料是主要的放气来源，其产生的主要污染物是环氧树脂中添加的增塑剂——邻苯二甲酸二辛酯（DEHP）。因此，本文选取DEHP 作为污染源进行敏感镜面上污染物沉积量的仿真计算，依据ASTM E1559Standard Test Method for Contamination Outgassing Characteristics of Spacecraft Materials，DEHP 的黏附系数在293.15 K时的测定值为0.011。

2 仿真方法及计算结果

分子污染物在高真空环境进行无规则热运动，此时流场速度为0，可用布朗运动模型来描述分子的热运动。扩散方程是从宏观角度描述分子因布朗运动形成的扩散现象的偏微分方程，可以用来描述污染物扩散以及吸附等物理过程，是解决复杂构型污染仿真分析难题的有力手段[23-25]。

2.1 扩散方程

当污染物分子在指定区域Ω内进行布朗运动时，分子由高密度向低密度方向运动。这一过程可以用偏微分方程中的扩散方程（热方程）描述[25]，其简要导出过程如下：

根据质量守恒，物质的密度流F与其密度u之间的关系可表示为

式中：x为空间位置；t为时间；∂Ω为区域Ω的边界；n为∂Ω的外法向。

由式(6)可知，u=u(x,t)表征空间位置x处在t时刻的物质密度，是构建扩散方程的关键变量。由Ω的任意性，根据Gauss-Green 公式，可将式(6)改写为

式(7)的物理意义是区域内物质质量随着时间的变化率，等于每一时刻经过区域表面流出的物质量。物质扩散特性决定了密度流F在密度场中与密度u分布的负梯度成正比关系，故可用密度负梯度的常数倍-a∇u表示，其中a为扩散系数，且a≥0。因此，扩散方程可以表述为

在仿真计算中，扩散系数a的取值为0.27，文献[26]中给出了DEHP 的各项相关参数。扩散方程单纯描述了物质的扩散，而污染物分子的产生需要引入源项，可用f(x,t)表示，则本文使用的扩散方程为

在处理实际问题的过程中，式(9)中：密度函数u(x,t)的量纲为(g·m-2)，ut表示密度的时间导数，则时间以小时（h）为单位的情况下方程左侧的量纲为(g·m-2·h-1)；方程右侧，源项f(x,t)表示密度生成或灭失的速率，故其量纲为(g·m-2·h-1)；而描述扩散的密度二阶空间导数项Δu的量纲与u(x,t)的量纲相同，亦为(g·m-2)，扩散系数a的量纲为h-1，故aΔu的量纲为(g·m-2·h-1)。可见，式(9)左右两侧的量纲匹配，可用来描述区域Ω中污染物分子密度随时间的变化情况。

2.2 模型建立与边界条件

在求解扩散方程的过程中，需要使用边界条件使方程定解，相机箱体内壁上污染物的反弹和黏附情况是必须考虑的边界条件，本文通过Gmsh 软件对相机箱体结构进行网格剖分，先对一维线进行离散，再利用曲线剖分的网格对曲面进行二维剖分，然后通过曲面的网格对体网格进行划分，最终生成具有规则三角网结构的网格剖分图，如图2 所示。遮光罩的放气污染大部分会直接逸散到结构开口外部，对结构内镜片的污染沉积量影响相对较小，因此本文在仿真计算中未考虑遮光罩部分的放气。完成剖分之后得到计算区域中的四面体网格，即计算单元。基于此网格，结合有限元法对扩散方程进行数值计算，进而完成模拟仿真。本文采用开源的有限元计算软件FreeFEM，计算中采用了线性元，即每个单元上的有限元空间基函数次数为1，同时时间离散采用具有较高计算效率的二阶隐式迭代格式。此计算策略在保证精度的同时也能够保持较高的计算效率。

图2 相机箱体结构的网格剖分三维图Fig.2 Three dimensional mesh splitting of the camera box structure

材料分子污染的出气特性对应于式(9)中的源项f(x,t)，该源项只在边界处有值且与出气特性相同。计算中，边界处产生污染物，即边界处的污染物密度升高；而扩散项描述污染物在整个空间中的扩散情况。源项放气和扩散项扩散的过程随着时间导数项ut迭代同时进行，由此可利用偏微分方程数值解法获得任意时刻区域中的密度分布和敏感镜面的污染物沉积情况，实现对复杂光学结构中分子传输与沉积行为的快速仿真。

2.3 污染物沉积量预估

设结构整体的温度均为T=293.15 K，则4 个敏感面历经3 年的污染物沉积量如表2 所示。

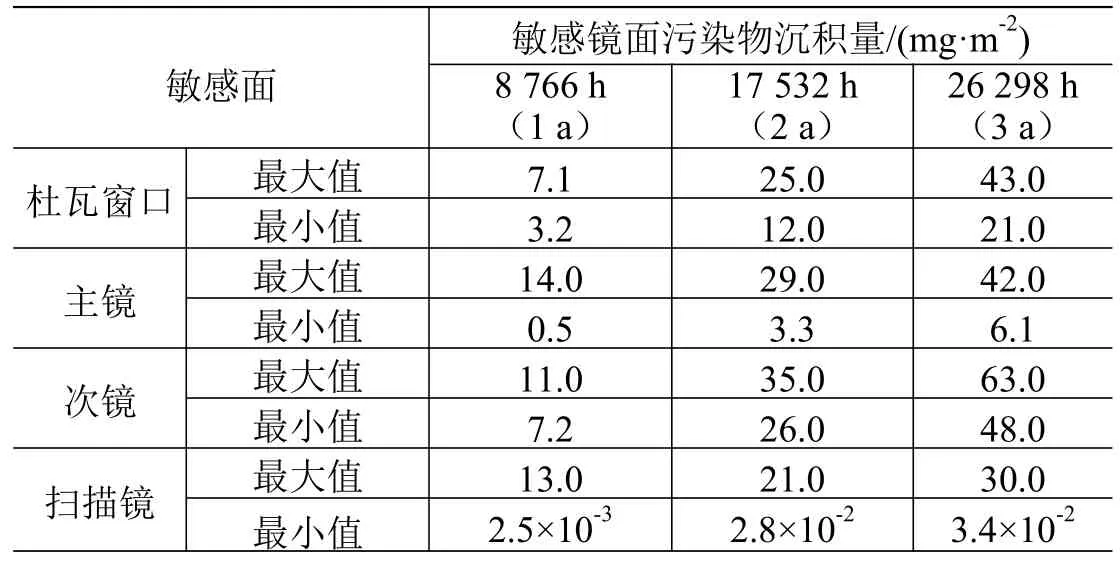
表2 敏感面污染物沉积数值模拟结果Table 2 Simulation results of contamination deposited on the sensitive lens surfaces

由图3 至图6 所示的污染沉积量分布计算结果，图中：x、y、z坐标轴为敏感镜面的尺寸，mm；右侧等值线为污染物沉积量，(g·m-2)。由结果可知，4 个敏感面的污染沉积量呈现边缘位置较高、中心附近位置较低的特点，这是敏感镜面边缘与污染源的距离较近所导致的。杜瓦窗口和次镜的污染物沉积厚度范围分布较窄，这是由于它们的尺寸较小导致污染物分布梯度较小；而主镜和扫描镜的尺寸较大，导致其边缘污染物较厚，而镜面中心污染物较薄。

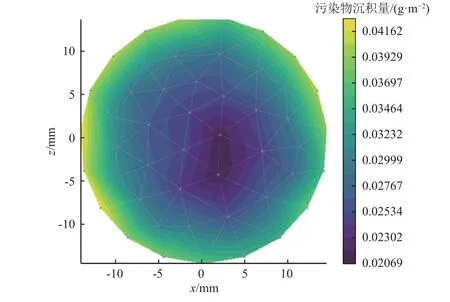
图3 杜瓦窗口3 年污染沉积量分布Fig.3 Distribution of contamination depositions on the surfaces of Dewar window

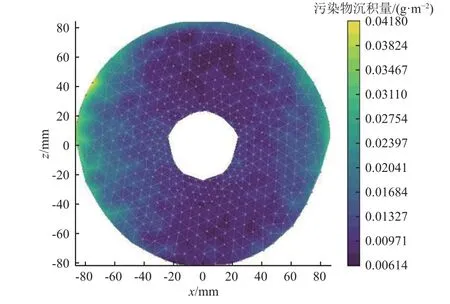
图4 主镜3 年污染沉积量分布Fig.4 Distribution of contamination depositions on the surfaces of primary lens

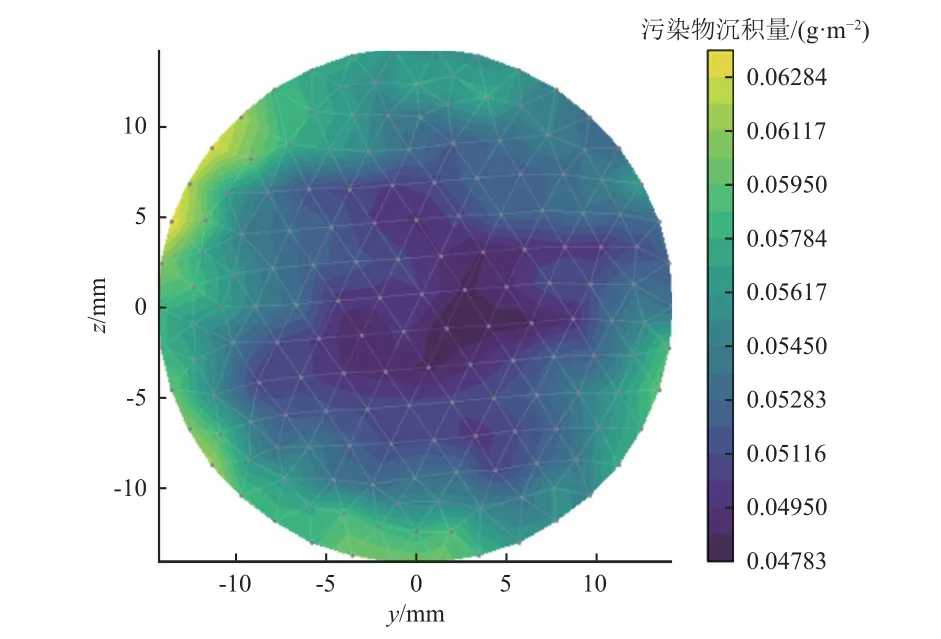
图5 次镜3 年污染沉积量分布Fig.5 Distribution of contamination depositions on the surfaces of secondary lens

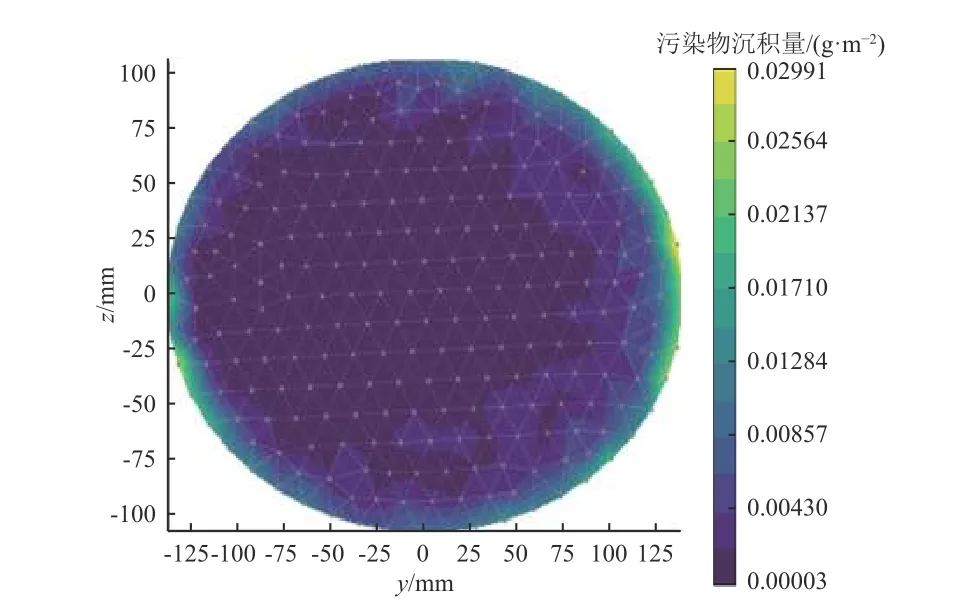
图6 扫描镜3 年污染沉积量分布Fig.6 Distribution of contamination depositions on the surfaces of scanning lens

另外，由表2 的数据可以看出，随着时间的延长，沉积量的变化趋势逐渐平缓，符合真空环境下污染物挥发的特性[27-30]。

3 光学载荷污染效应分析

为验证污染物对光学载荷的污染效应，本文以DEHP 作为污染源，利用真空加热设备对其沉积量、沉积厚度以及敏感镜面的光学性能进行了地面污染效应试验研究。真空舱体内置的加热台上放置盛有DEHP 的铝盒，将镜片固定在铝盒上方抽真空并加热，使DEHP 蒸发并冷凝在光学镜片表面，通过控制试验时间得到不同厚度的污染，使用椭偏仪测量DEHP 污染的厚度，并利用紫外–可见–近红外分光光度计对污染镜片在250～1750 nm 波段的平均透过率和反射率进行测试，通过计算得出光学性能变化率，结果见表3。

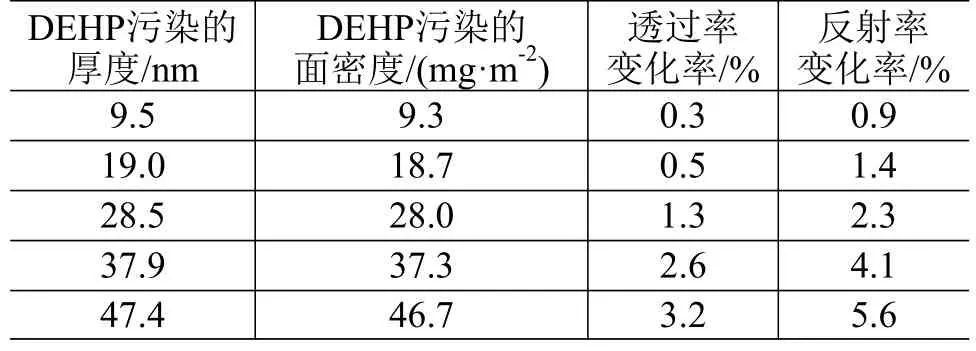
表3 光学镜片的污染量与光学性能衰减情况Table 3 Contamination deposition and attenuation of optical properties of lens

由上述所得测试数据，将不同污染厚度对应的透过率和反射率相对衰减变化的数据进行线性拟合，结果如图7 和图8 所示。

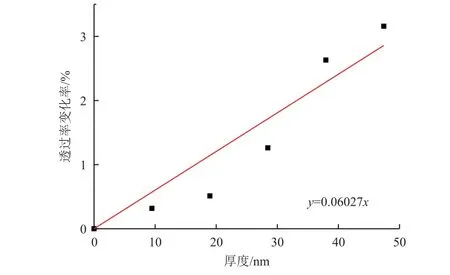
图7 污染厚度与透过率变化率的线性拟合（R2=0.954）Fig.7 Linear fit chart of contamination thickness and rate of transmittance change (R2=0.954)

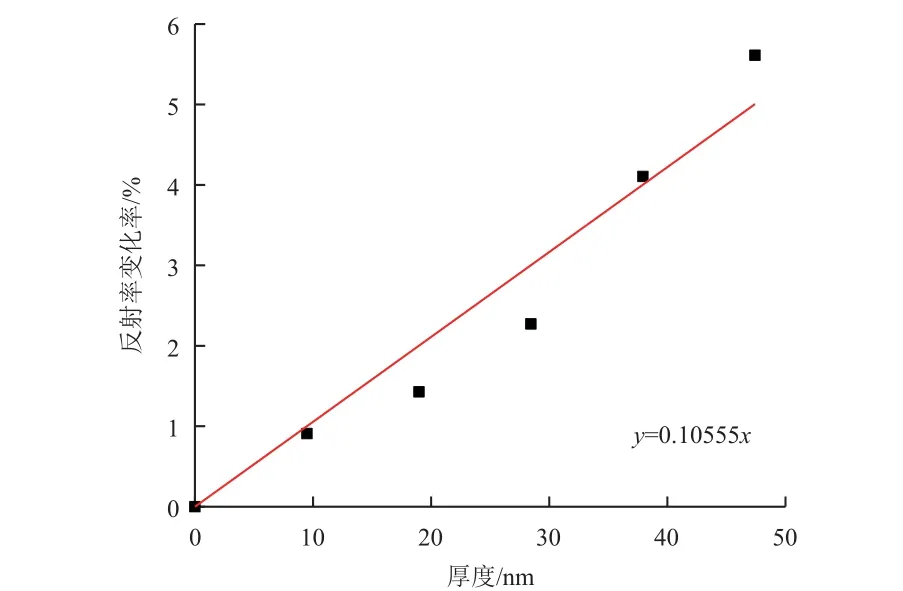
图8 污染厚度与反射率变化率的线性拟合（R2=0.978）Fig.8 Linear fit chart of contamination thickness and rate of reflectance change (R2=0.978)

依据表2 污染模拟结果以及污染厚度与镜片光学性能的线性拟合关系，可计算出各镜片3 年后的光学性能变化情况，见表4。

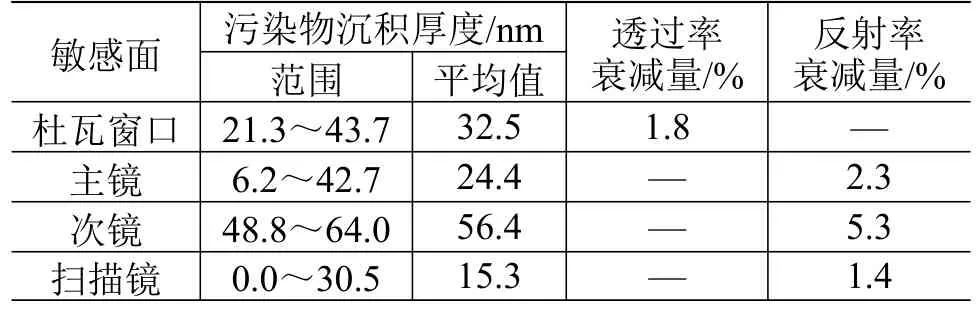
表4 3 年后各镜片的光学性能衰减量Table 4 Transmittance and reflectance attenuation of each lens after three years

由表4 可知：杜瓦窗口的透过率衰减量为1.8%；主镜、次镜和扫描镜的反射率衰减量分别为2.3%、5.3%和1.4%。以上数据表明，沉积在镜片表面的污染分子对光学性能具有一定的衰减作用，可见光学载荷在轨运行期间存在被污染进而影响其性能的风险，建议设计师在材料选择和结构设计中予以适当的考虑，减少污染引起的负面影响。

以上结果是污染物在敏感面表面形成均质膜层的理想条件下所得，而当污染厚度达到一定阈值后可能会形成液滴，导致敏感面光学性能衰减的实际值大于理论分析值，而这种液滴的形成很难预测，取决于污染物的种类及其与敏感面的亲和力，甚至光化学反应也会引发液滴的形成[31]。