纤维动态张力校准装置设计与测量模型验证
2023-05-12左睿奇张鹤宇
左睿奇,李 博,*,杨 军,王 霞,张鹤宇
(1.北京长城计量测试技术研究所,北京 100095;2.北京理工大学 光电学院,北京 100081)
0 引言
在复合材料成型工艺中,纤维缠绕技术开发最早且生产效率高,其相关制品具有比强度高和比模量高、耐高温、可靠性高等优势,被广泛应用于导弹、机枪枪架、火箭发射筒等军用装备,以及发动机机匣、燃料胆箱、飞机副油箱等航空航天产品。
缠绕成型过程中,纤维张力的准确测量和控制是保障复合材料制品机械性能、生产效率和良品率的重要条件,而材料拉伸、机械振动产生的张力波动对动态张力校准与测量精度提出了更高要求。目前,国外针对高端制造的纤维缠绕设备与技术对我国实行禁运。在柔性体张力计量领域,可查到的研究成果有针对电机定子齿形线圈建立的缠绕张力解析模型[1],通过Ident 参数辨识方法拟合的纤维缠绕动态张力模型[2]等,但未找到张力专用测量与校准装置相关研究的公开资料,考虑测量装置与被测对象耦合影响的研究成果也鲜有披露。我国的张力测量模型研究集中于接触式纱线张力传感器[3],对纤维张力控制系统动力学的研究具有一定启发意义[4],然而缺少针对张力传感器的专业校准设备和方法,仅有少数悬臂梁式张力传感器可以在力值标准机上进行静态校准,大多数滚轮式、导辊式张力传感器处于无法校准的状态,故亟需填补张力传感器校准设备与方法研究的空白。
本文从纤维缠绕张力校准技术的应用需求出发,以理论分析为基础进行张力校准装置结构设计;随后通过虚拟样机刚柔耦合建模与ADAMS 动力学仿真,优化尺寸参数并验证理论模型的可靠性,旨在为开展纤维缠绕张力在线校准奠定基础。
1 校准系统动态张力分析
1.1 张力校准装置工作原理
要研制针对纤维缠绕张力的校准装置,首先需理解纤维缠绕的工艺原理,通过对纤维缠绕系统的分析,确定纤维动态张力校准的基本原理和校准装置基本结构,建立动态张力与其他标准量的联系。
纤维缠绕的工艺原理为[5]:通过芯模和喷嘴的相对运动,在控制系统的作用下将浸渍树脂的连续纤维按给定张力规律缠绕在芯模表面,再经过室温固化或加热固化制成有固定形状的制品。
而纤维张力动态校准系统就是通过输入标准动态力模拟纤维缠绕装置上的真实张力波动,通过三点弯曲测量结构[6]复现在线张力测量环节,将纤维缠绕运动转换为重物的近似正弦振动,从而通过量值溯源实现对张力传感器的动态校准及测量误差分析。比较纤维缠绕系统与校准系统的结构如图1 所示。
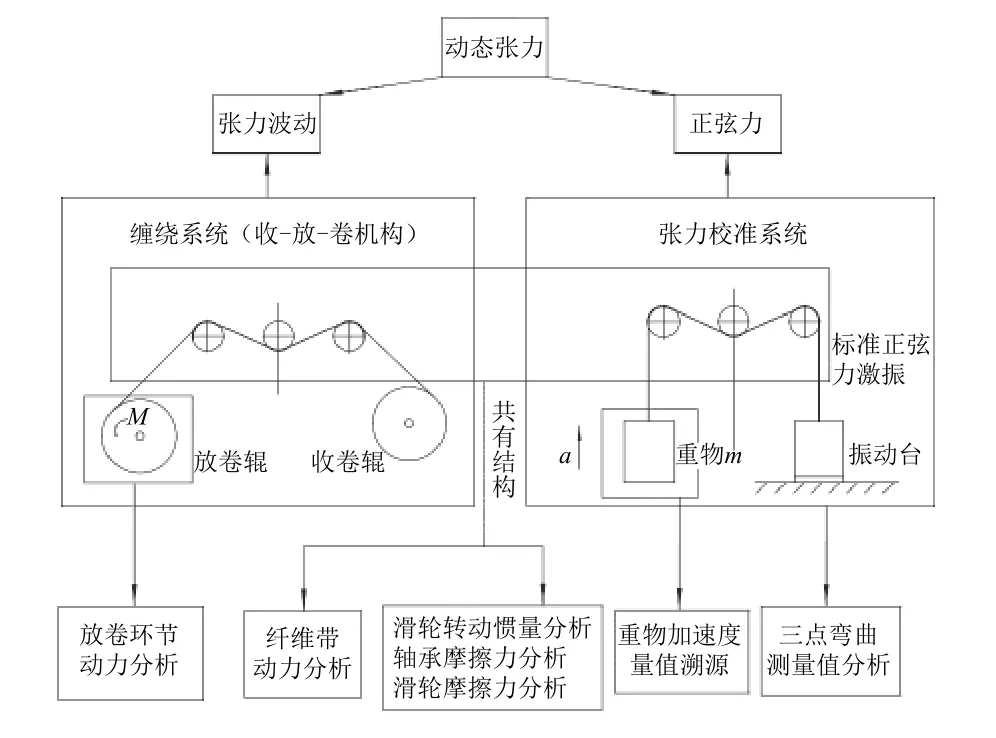
图1 缠绕系统与校准系统结构对比Fig.1 Structure comparison of winding system and calibration system
在张力校准系统中,纤维带一端与振动台固连,一端与重物(标准质量块)绑定,启动前,纤维带内预张力与重物重力平衡;启动后,振动台正弦激振,带动纤维带纵向振动,纤维带依次绕过3 个定滑轮使重物振动,滑轮随纤维带绕轴心往复转动,张力传感器安装在中间滑轮处,测量动态张力。
根据牛顿第二定律,理想情况下整根纤维带上各点处的张力相等,均可简化表示为
式中:m为重物的质量,可溯源到质量标准;a为重物上表面的运动加速度,可以按照加速度原级标准,通过激光干涉系统测量并实现溯源。通过这种方法,动态张力可以溯源到质量、长度和时间这3 个国际单位制基本单位,初步建立起校准所需的量值溯源路径。
然而,实际测量中,必然存在材料形变、摩擦及环境影响等非理想因素,需进一步分析并建立测量点处的动态张力方程,故将张力校准系统分为纤维带、纤维带−滑轮−轴承耦合结构以及测量结构,并对各部分的张力分别进行理论分析。
1.2 动态张力理论方程
考虑到3 个滑轮之间纤维带跨度较小,且存在预张力,可忽略该段纤维带形变对张力的影响;悬垂段张力在纤维带上的分布为
式中:λ为纤维带线密度;l为纤维带悬垂段长度;k0为加速度修正因子,通过实验获得;g为重力加速度。
当张力校准系统产生正弦激振时,纤维带各个微段均做某方向上的往复运动,这一过程近似于缠绕系统放卷辊启停的过渡态:纤维带开始运动时要能够带动滑轮旋转,通过张力变化实现滑轮的角加速旋转;纤维带反向运动时,改变滑轮的转动方向也需要张力变化来提供能量。因此要研究滑轮−轴承−轴结构对张力波动的影响。单滑轮与纤维带的截面如图2 所示,图中:;r0、r1和r2分别为滑轮轴、轴承和滑轮的外半径;F1和F2分别为绕进和绕出该滑轮两端的纤维带张力。
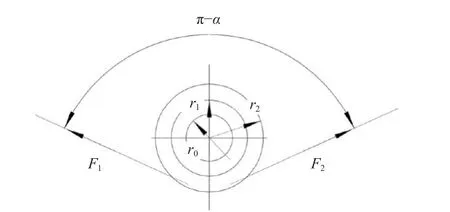
图2 纤维带−滑轮−轴承截面示意Fig.2 Cross section diagram of fiber band-pulley-bearing
其中,滑轮转动惯量引起的张力波动为
式中:J为滑轮转动惯量;ωo为滑轮转动角速度,通过纤维线加速度计算;N为滑轮轴数;Wz为滑轮轴长度;ρz为滑轮材料密度;az为滑轮转动加速度。
由式(3)可见,张力波动值与重物上表面加速度、滑轮轴数和轴质量等参数成近似正比关系,滑轮转动惯量的增加将使张力波动大幅增加,因此,滑轮结构设计是张力校准装置设计的重要环节。另外,还需考虑滚动轴承摩擦力矩
式中:μb为轴承摩擦系数;Fb为轴承载荷。
在校准系统中,轴承受纤维带传递的压力远大于横向振动产生的轴向力,故可通过滑轮两侧纤维带上张力计算轴承载荷,建立力矩平衡方程ΔFbi=μbr0[Fi1cosαi1+Fi2cosαi2±Gb]/r2,计算得出轴承摩擦引起的动态张力。以三点弯曲张力测量处的中间滑轮为例,
式中:Gb为滑轮、轴承外圈及其他配件等转动部件的总重,当张力分量Fi1cosαi1与重力方向一致时,Gb前取正号;i为轴承所在轴标号,取1~N,N为滑轮轴数量;α为缠绕包角,αi1为张力Fi1方向与铅垂线的锐角夹角,αi2为张力Fi2方向与铅垂线的锐角夹角。
最后,考虑纤维带与滑轮间的库仑摩擦力。在滑轮跟随纤维带平稳转动时,接触面处只需考虑静摩擦力;而在高频振动的校准实验中,滑轮转动方向频繁改变使得纤维带容易发生打滑,在临界摩擦状态取对应转角dθ的纤维微段进行分析,如图3所示。
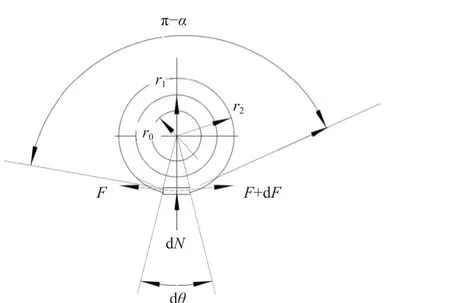
图3 纤维微段受力分析Fig.3 Stress analysis of fiber microsegment

式中Fr为稳态时纤维带内的张力。对于由静止状态启动的缠绕系统,Fr=F(l)即为纤维带的预张力。由机理分析过程可知,缠绕包角α越大,稳态时纤维带内张力越大,则越容易产生较大张力波动。
结合以上分析,得到校准系统的动态张力理论方程为
式(8)建立了张力测得值和其他标准量、可测量值的关系,等式右边的待测量值中:重物加速度随时间变化,可用已校准的加速度计或外差式干涉仪[7]测量;重物质量可通过标准质量块组调节;其余常量在单次实验中保持不变。由此可获得动态张力的测量模型。
2 校准装置设计及刚柔耦合模型
2.1 张力校准装置设计
在张力校准装置基本结构和动态张力机理分析的基础上,考虑张力传感器、加速度传感器安装位置及振动台外形尺寸,进行张力校准装置设计,并根据初步设计结果建立ADAMS 虚拟样机模型,通过刚柔耦合模型的动力学仿真进一步优化装置尺寸参数及结构。
张力校准实验装置如图4 所示,考虑到纤维带与滑轮包角带来的影响,以及机械加工精度,为定滑轮拟定了5 种定位尺寸。设纤维带从左至右依次绕过滑轮1~5,影响三点弯曲法张力测量结果的最主要尺寸参数是滑轮2 与滑轮4 安装轴轴线的水平间距,通过刚柔耦合模型可确定最佳水平间距,以使滑轮2、滑轮4 之间纤维带柔性变形对张力值的影响最小为优。
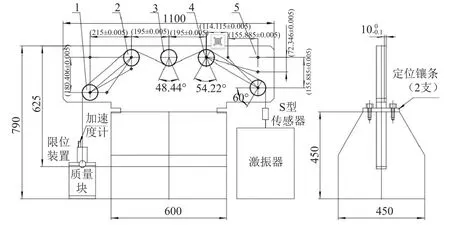
图4 动态张力校准实验装置Fig.4 Experimental device for fiber dynamic tension calibration
待确定的张力校准装置参数为图4 中滑轮2与滑轮4 安装轴轴线的水平间距。根据装置结构和机械加工精度,水平间距可选择390.000 mm、504.115 mm、618.230 mm、774.115 mm 或930.000 mm,因此需通过仿真控制变量分析改变水平间距对张力波动与误差的影响,以确认最优结构参数。
柔性体的高频激振是通过正弦力法校准张力传感器的主要技术难点,应确定振动台的最佳工作频率及纤维带内张力范围,通过仿真分析确定该装置的最佳工作状态,即在何种状态下系统内能产生可测得的动态张力,是否可以实现预期功能,并据此确定测量方案。
2.2 ADAMS 刚柔耦合模型的建立
为实现对校准装置的仿真分析,需进行虚拟样机简化建模,其中:滑轮、重物可视为近似刚体;振动台可应用位移输入或力输入模拟;而纤维带因其材料特有的弹性特性必须作为柔性体引入刚性系统。这就需要解决复杂的柔性连续体建模及多体系统刚柔耦合约束问题。
目前已有的建模方法有:1)由ANSYS 向动力学仿真软件导入MNF 模态中性文件[8],此方法必须设置刚柔耦合连接节点,而带状纤维与滑轮的面面接触必然导致仿真分析失败;2)基于ADAMS/Cable 模块将绳索离散成小球进行柔性体建模[9],此方法无法灵活调整为带状模型;3)基于ADAMS/Bushing 的柔性体建模,该方法近年被应用于钢丝绳提升多体系统的建模,原理是手动将钢丝绳离散为微元再进行建模[10],小单元之间添加六自由度轴套力(Bushing)关联。综合本研究的仿真需求选定方法3,外部编程导入CMD 文件辅助建模。
实际上,方法3 尚未被应用于钢丝绳以外柔性材料的建模。本研究在刚柔耦合建模中解决了2 个难题:1)纤维带微段立方体模型的定位;2)在高频振动仿真中使刚体滑轮跟随柔性连续体往复转动。
通过设置MARKER 点的方式标记纤维带截面中心点,由此构成定位坐标,应用bend 命令使纤维带绕过该点所在轴线弯折,如图5 所示。由于尺寸精度均在10-9mm 量级,且两微段间相互渗透体积较小,可通过ADAMS 建模检查,不影响运动仿真。
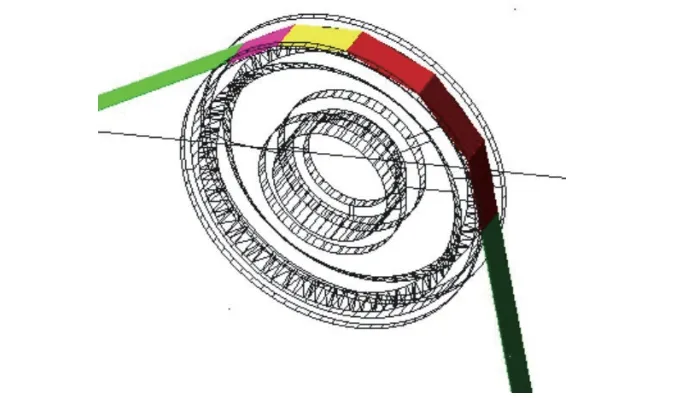
图5 纤维带弯折建模Fig.5 Modeling of fiber band bending
综合应用基于碰撞函数的Contact 法以及Revolute joint 旋转副,减弱了纤维带与滑轮在仿真开始(释放)瞬间的碰撞,使得滑轮易于跟随纤维带的运动,特别是提升了高频正弦激振下仿真解算的成功率,最终完成了校准装置ADAMS 刚柔耦合模型的建立,如图6 所示,左侧圆柱体为标准质量块,右侧纤维带下端连接哑物体小球便于模拟振动台作用力。
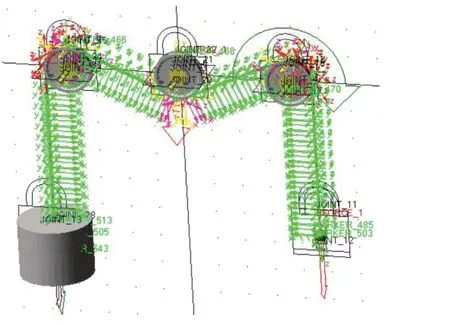
图6 纤维动态张力校准装置刚柔耦合模型Fig.6 Rigid-flexible coupling model of fiber dynamic tension calibration device
仿真前,要考虑的首要问题是纤维带约束方案,即外载荷的输入位置,需通过仿真确定哪种实验方案易于实现纤维带的高频振动。可选方案包括:
方案1——纤维带一端与重物相连,重物悬空;纤维带另一端与振动台绑定,从右至左通过振动台面的位移带动纤维带−滑轮−重物运动。
方案2——纤维带一端与重物相连,重物通过弹簧与地面相连;纤维带另一端与振动台绑定,从右至左通过振动台面的位移带动纤维带−滑轮−重物运动。
上述方案中,若要实现量值溯源,须采用方案1进行仿真及实验;但在实际测量中,由于柔性体高频振动时,张力和加速度将沿纤维带衰减,难以在较远端测得加速度,故采用方案2,在振动过程中保证纤维带始终张紧,整个多体动力学系统可视为近似刚体系统,拓宽实验频率范围。
3 动力学仿真
通过仿真模型调整和边界条件设置进行张力校准仿真,并依据仿真结果对张力校准装置进行结构及参数优化设计,在优化后的装置仿真模型基础上验证动态张力测量模型。
3.1 张力校准装置结构优化
在重物端连接弹簧,并将弹簧与地面连接,每隔10 个微元段取点测纤维带内张力,在正弦力波峰处取点,如图7 所示,各段内张力差值不超过0.05 N。该方案显著降低了纤维带弹性形变对内张力的影响,仿真结果更为理想。
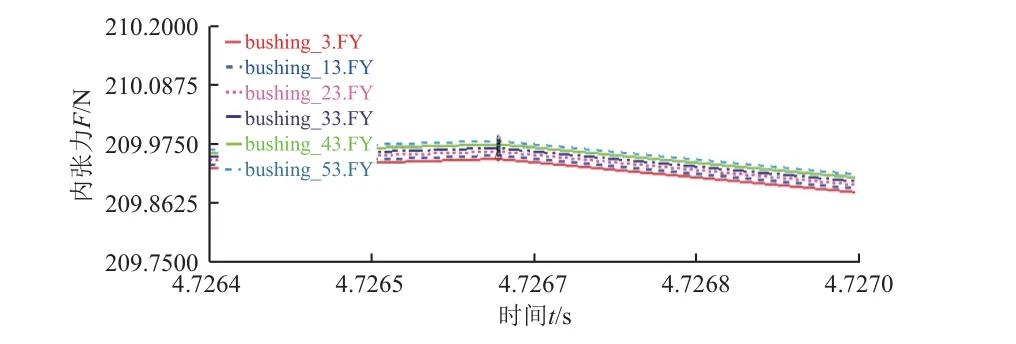
图7 210 N 内张力沿纤维带悬垂方向的变化Fig.7 Variation of tension in 210N along the drape direction of the fiber band
根据2.1 节中的结构参数,改变模型中滑轮的水平间距,对不同纤维带−滑轮包角进行微段划分,选取左端滑轮右出绳微段与中间滑轮左入绳微段,控制时间变量,分析二者在纤维带轴向上的最大张力差值,得到该张力差值随滑轮轴水平间距的变化关系如图8 所示。

图8 张力差与滑轮水平间距的关系Fig.8 Tension difference vs.horizontal spacing of pulley
滑轮轴水平间距同时影响着纤维带与3 个滑轮之间的包角,随着水平间距的增大,纤维带与滑轮之间包角减小,与滑轮间摩擦力下降,存在打滑风险;此外,纤维带跨度的增大也增加了张力波动,故当水平间距过大时,3 点间张力差值将大幅增加。理论测量模型与仿真结果互为验证,故选取水平间距为390.000 mm 的设计参数,缩短绕过全部滑轮的纤维带长度,并进一步提高装置结构的紧凑性。至此通过仿真分析实现了对实验方案和校准装置结构的优化。
3.2 测量模型验证
在重物质心位置测量加速度,在与中间滑轮接触的纤维带中点微段质心处测量张力,模拟实际张力校准中重要参数(加速度)的测量,得到纤维带张力−时间、重物加速度−时间曲线(如图9 所示),可见,在较低频率(10 Hz)下,系统可以很好地响应振动台输入的正弦激振力。
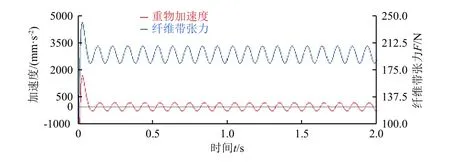
图9 10 Hz 下重物加速度/纤维带张力−时间曲线Fig.9 Weight acceleration/fiber band tension vs.time at 10 Hz
修改控制振动的位移输入参数,当重物质量较小、激振频率较低时,重物及纤维带下端存在较明显的横向摆动,可见纤维带预紧力、张力不足时横向振动影响较大。
输入正弦力F=10sin(2π·1000t),将激振频率提升至1000 Hz,振幅20 N,输出的纤维带张力−时间、重物加速度−时间曲线如图10 所示。在高频激励下,结合时域信号与频谱分析,仍有张力输出,但其幅值较小,主要由于纤维材料刚度不足导致能量传递存在耗散。在实际生产中,张力传感器使用的频率范围多在数百Hz 以下,本研究设计的张力校准装置可以实现1000 Hz 以下正弦激励发生,满足大多数情况的动态校准需求。
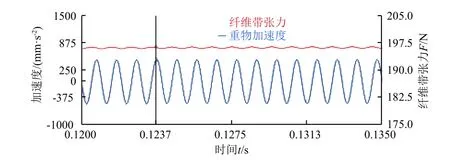
图10 1000 Hz 下重物加速度/纤维带张力−时间曲线Fig.10 Weight acceleration/fiber band tension vs.time at 1000 Hz
在振动频率100 Hz 正弦输入力、悬挂10 kg 砝码工况下,将ADAMS Postprocessor 输出的仿真数据导入MATLAB,与依据1.2 节理论方程算得的张力−时间曲线对比,如图11 所示。可见:前0.7 s 内,由于重物重力瞬间加载,纤维带测力位置张力不能及时响应,理论计算与仿真模型测量的动态张力值间存在较大偏差;0.7 s 后达到稳态,理论计算与仿真模型测量的动态张力值趋于完全一致,验证了张力校准系统测量模型的合理性。
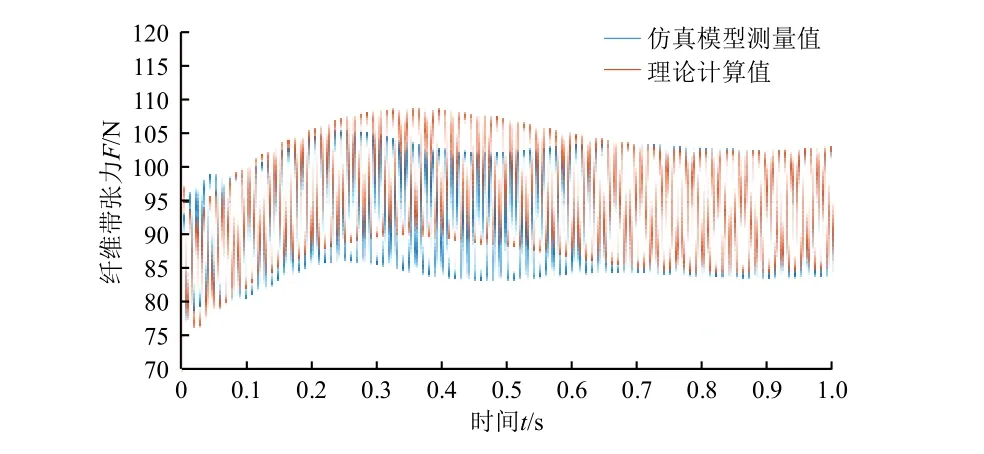
图11 校准系统动态张力仿真模型测量与理论计算值比较Fig.11 Comparison of dynamic tension simulation model measurement and theoretical calculation of the calibration system
4 结束语
本文通过理论分析与仿真实验的相互印证,完成了纤维动态张力校准装置的设计与优化,确定了可应用于校准系统的测量模型,实现了理论、仿真分析结果对实测方案的指导,为纤维缠绕动态张力的在线校准奠定了基础。
纵览已有分析结果,滑轮结构带来的张力波动可能成为实测中的主要误差来源;此外,过渡态下动态张力的大幅变化,提示了纤维带横向偏摆振动的可能影响,在未来的实验研究中应予重点关注。
