一种基于联邦滤波的SINS/GNSS/RA 弹载多源组合导航算法

李杰，梁玉琴，李昃雯，秦 硕，程遵堃

（上海航天控制技术研究所，上海 201109）

0 引言

弹载导航系统提供的位置、速度和姿态信息，能够指引导弹按照既定的弹道飞行，从而对目标实现精确打击。弹载导航系统需要工作在全天候、高动态环境中，目前多采用惯性/卫星（Ship’s Inertial Navigation System/Global Navigation Satellite System，SINS/GNSS）组合导航的方式［1］。SINS 不需要接收外部信息，是一种完全的自主式导航系统，但由于其工作原理的特殊性，长时间单独运行导航信息会逐渐发散［2］，因此需要以其他导航信息，如GNSS 提供的位置和速度等进行修正。然而GNSS接收机易受干扰，常常因为接收不到卫星信号而导致丢星，无法提供组合导航融合信息，使得导弹的打击精度受到影响。

单一的SINS/GNSS 组合导航系统难以满足导弹精确打击的需求，因此辅助传感器的研发和选用极为迫切。在众多高程测量传感器中，雷达高度表（Radar Altimeter，RA）具有体积小、功耗低、精度高且测高范围大等特点［3］，常用于航空航天设备中。因此选取雷达高度表为弹载导航提供信息源参与SINS/GNSS 信息融合，能够极大地提升弹载导航系统的鲁棒性和可靠性。

本文基于发射惯性系，构建了SINS/GNSS/RA弹载多源组合导航系统联邦滤波融合框架，并推导了数学模型，通过弹道仿真试验验证了该算法的正确性，为弹载多源组合导航系统的研究提供了思路。

1 联邦卡尔曼滤波融合框架

SINS/GNSS/RA 弹载多源组合导航系统选取SINS 作为公共参考系统，构建SINS/GNSS 和SINS/RA 两个子滤波器，联邦滤波算法结构如图1所示。

图1 联邦滤波算法结构Fig.1 Structure diagram of the federated filter algorithm

联邦滤波的状态方程和量测方程为［4］

式中：F(k)、G(k)、X(k)、w(k)分别为k时刻状态转移矩阵、系统噪声驱动矩阵、状态矢量和系统状态噪声矢量；X(k+1)为系统k时刻到k+1 时刻状态估计值；Zi(k)、Hi(k)和vi(k)为系统k时刻子滤波器i的量测矢量、量测矩阵和量测噪声矩阵。

联邦滤波信息融合方法主要包含4 个环节［5-6］：

1）子滤波器信息的时间更新

式中：Pi(k+1|k)、Qi(k+1|k)分别为子滤波器i状态一步预测误差估计协方差矩阵和一步预测系统噪声方差矩阵。

2）子滤波器信息的量测更新

式中：Ki(k)、Ri(k)分别为子滤波器i增益矩阵和量测噪声方差矩阵。

3）主滤波器信息融合，假设子滤波器的数量用N表示，则信息融合得到状态量全局最优估计和全局最优估计协方差阵：

4）子滤波器信息分配，子滤波器信息Pi(k)、的分配按照如下原则进行：

式（5）中，信息分配系数βi(βi＞0)满足信息守恒原理：

通过以上4 个环节，可以实现多个导航信息源测量值对状态的最优估计，从而得到最优融合后的导航输出信息。

2 发射惯性系下SINS/GNSS/RA 组合导航系统数学模型

由于联邦滤波将SINS 作为公共参考系统，因此选取发射惯性系下SINS 的基本导航参数误差和惯性仪器参数误差共15 维误差信息作为状态变量［7］，用X(k)表示为

式中：φx、φy、φz为发射惯性系下姿态失准角；δVx、δVy、δVz和δx、δy、δz分别为发射惯性系下x、y、z3个轴向速度和位置误差；εx、εy、εz和∇x、∇y、∇z分别为弹体坐标系下陀螺仪常值漂移和加速度计常值偏置。

通过姿态失准角、速度、位置和惯性器件误差传播方程构建式（1）中的状态方程，F(k)、G(k)和w(k)的具体参数见文献［7］，此处不再赘述。

2.1 SINS/GNSS 子滤波器

SINS/GNSS 子滤波器量测方程由3个轴向速度和3个轴向位置2部分量测方程构成［8-12］，具体如下：

1）速度量测方程：

式中：Vsx、Vsy、Vsz为由SINS 解算的发射惯性 系下x、y、z3 个轴向速度值；Vgx、Vgy、Vgz为由GNSS 输出的速度转换到发射惯性系下投影在x、y、z3 个轴向上的分量；vv为GNSS 接收机速度测量误差矢量；Hv为速度量测矩阵。

2）位置量测方程：

式中：Xs、Ys、Zs为由SINS解算的发射惯性系下x、y、z3 个轴向位置值；Xg、Yg、Zg为由GNSS 输出的位置转换到发射惯性系下投影在x、y、z3 个轴向上的分量；vp为GNSS 接收机位置测量误差矢量；Hp为位置量测矩阵，

由式（8）和式（10），可得到SINS/GNSS 子滤波器的量测方程：

式中：ZGNSS、HGNSS和vGNSS分别为SINS/GNSS 子滤波器系统的量测矢量、量测矩阵和量测误差矩阵。

2.2 SINS/RA 子滤波器

装载有RA 的导弹在飞行过程中，以一定的频率向地球表面发射雷达脉冲［13-25］，导弹上的雷达信号接收装置接收到回波后，通过时间间隔Δt可以得到RA 的测量值H′［2］，具 体为

式中：c为电磁波传递速度。

为了获得导弹实际所在位置的海拔高度，需要对测量值H′进行补偿，具体如下：

式中：Δh为补偿值，由当地海拔等因素确定。

发射惯性系下导弹位置如图2 所示。图2 中，Re0、Re分别为发射点和当前导弹所在位置的地球半径。

图2 发射惯性系下导弹位置Fig.2 Schematic diagram of the missile position under the launch inertial system

在发射惯性系即Ol-XlYlZl系下，位置矢量OlP与发射点水平面夹角用θo表示，满足式（15）：

式中：x、y、z为导弹所处位置在发射惯性系下的坐标。

将坐标转换为海拔高度值为

Hs与Hr作差，可得

式中：vh为误差项，受导航误差和RA 测量精度影响。其中，

综上，构建SINS/RA 子滤波器的量测方程为

其中，量测矩阵HRA为

3 仿真校验

3.1 仿真条件

1）设计导弹为垂直发射，发射点初始位置：纬度32.0°，经度118.0°，高度0 m；发射方位角为90°；主动段为70 s，全程飞行时间为357 s。

2）GNSS 采样频率为1 Hz，RA 的采样频率为10 Hz，SINS 采样频率为200 Hz；联邦滤波融合周期为1 s。

3）陀螺仪常值漂移为0.5（°）/h，白噪声为0.1（°）/h；加速度计常值偏置为1 mg，白噪声为0.5 mg。GNSS 位置误差为10 m，速度误差为0.1 m/s。RA的测量误差为30 m。

3.2 仿真结果及分析

通过上述条件生成弹道轨迹，如图3 所示。

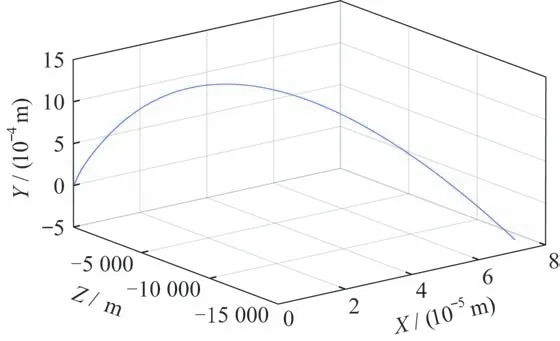
图3 发射惯性系下弹道轨迹Fig.3 Ballistic trajectory in the launch inertial coordinate system

生成发射惯性系下SINS、GNSS 和RA 仿真数据后，利用联邦滤波算法进行信息融合，得到发射惯性系下的位置误差曲线，如图4 所示。

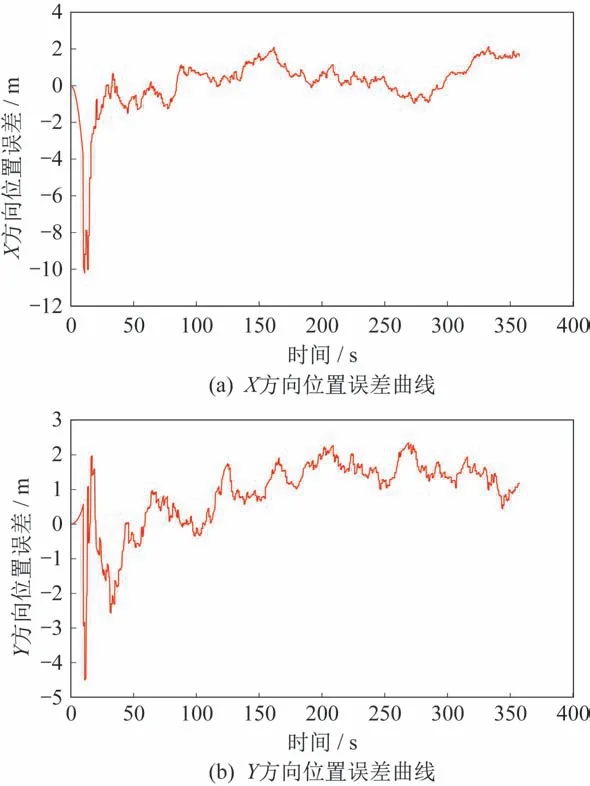
图4 发射惯性系下X、Y和Z 3 个方向位置误差曲线Fig.4 Position error curves of the X-，Y-，and Zdirections in the launch inertial coordinate system

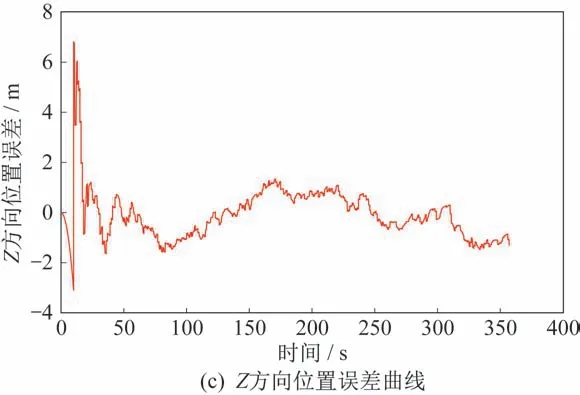
续图4 发射惯性系下X、Y和Z 3 个方向位置误差曲线Continue Fig.4 Position error curves of the X-，Y-，and Zdirections in the launch inertial coordinate system

由图4 可知，本文所设计的SINS/GNSS/RA 多源组合导航系统使用联邦滤波进行信息融合后，位置误差能够在短时间收敛，且波动幅度较小，能够得到稳定的导航位置信息。计算x、y、z3 个方向位置的均方根误差分别为1.48、1.34 和1.03 m，由此可知，导航系统输出的导航定位结果具有较高的精度。

本文基于联邦滤波的弹载多源组合导航算法，旨在提高弹载导航系统的稳定性和可靠性，在GNSS 失效的情况下，依然可以为导弹提供较为准确的导航定位信息。因此，设计仿真试验，生成一组仿真数据，在导弹飞行250 s 时，对GNSS 施加干扰，使其处于丢星状态，分别使用本文设计的SINS/GNSS/RA 多源组合导航系统与传统的SINS/GNSS 组合导航系统进行信息融合，得到位置误差对比曲线如图5 所示。

由图5 可知，在导弹飞行250 s 即GNSS 未受干扰之前，SINS/GNSS/RA 多源组合导航系统和SINS/GNSS 组合导航系统两者误差相近，都有较高导航定位精度；在导弹飞行250 s 之后，SINS/GNSS 组合导航系统x、y、z3 个方向位置误差均快速发散，而SINS/GNSS/RA 多源组合导航系统误差虽然也缓慢发散，但在短时间内，依然可以为导弹提供较可靠的导航定位信息。

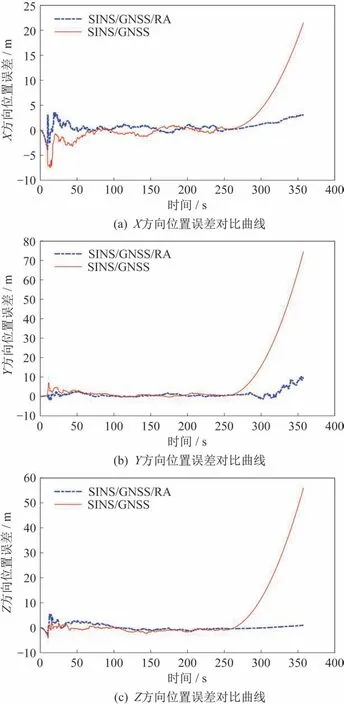
图5 发射惯性系下位置误差对比曲线Fig.5 Comparative position error curves in the launch inertial coordinate system

在GNSS 受到干扰后，SINS/GNSS 子滤波器失效，联邦滤波主滤波器只融合了SINS/RA 的处理结果。分析SINS/RA 子滤波器的量测方程可知，SINS/RA 子滤波器能够对位置误差进行估计，使得联邦滤波信息融合后可以在一定程度上对导弹的位置进行修正，从而保证了导弹的打击精度。

4 结束语

本文分析了导弹传统SINS/GNSS 组合导航系统的缺陷，提出了基于联邦滤波的SINS/GNSS/RA 多源组合导航算法。通过弹道仿真试验，验证了导航算法的正确性。在GNSS 受干扰的情况下，将本文设计的弹载SINS/GNSS/RA 多源组合导航系统与传统SINS/GNSS 组合导航系统作对比，结果表明，本文设计的导航系统具有更高的鲁棒性和可靠性，并依然能够在一定时间范围内保证导弹的打击精度。