卫星在轨分离地面试验方案设计及动态仿真分析

张晓亮，张晓彤，刘福寿，孙加亮，文浩，金栋平

（1.南京航空航天大学 航空航天结构力学及控制全国重点实验室，江苏 南京 210016；2.上海卫星工程研究所，上海 201109；3.南京林业大学 土木工程学院，江苏 南京 210037）

0 引言

为提高运载火箭利用率和运载效率，一箭多星发射技术得到国际宇航界的广泛关注，其中多星分离成为一箭多星发射之关键技术［1-4］。相比于单星发射，一箭多星在技术方案和分离程序上均有很多不同之处。研究一箭多星在轨分离策略，以及在分离过程中如何避免卫星之间的干扰和碰撞，显得尤为重要。为保障卫星能够在轨顺利分离，需要在地面开展相关的分离试验及动态模拟。

在一箭多星卫星在轨分离地面试验软硬件方面，韩非等［5］设计由气浮零重力平台、卫星运动模拟器和地面测量系统等组成的航天器在轨分离运动与控制地面模拟试验系统；HUANG等［6］详细介绍了适用于卫星地面分离实验的气浮实验台的硬件、软件结构。上述工作虽然为卫星分离地面实验奠定了良好软硬件的基础，但是设计卫星与其支撑结构为一体，无法拆卸。由于没有卫星的支撑结构，因此如果需要更换卫星，则需要重新进行仿真器的设计。

关于卫星分离动力学仿真建模方法，通常采用ADAMS 等软件进行建模分析［7-9］，部分学者采用姿态动力学方法进行分离动力学分析。如蒋超等［10］采用欧拉四元素表示卫星分离前后的姿态，并结合动量定理和角动量定理进行动力学建模。沈晓凤等［11］、滕来等［12］、张华等［13］均采用欧拉角描述卫星姿态，在计算小数量的卫星分离仿真时，使用欧拉四元素或者欧拉角表述卫星分离前后的姿态比较直观，但是随着卫星数量增加，在描述卫星分离姿态时，要想在同一惯性系下描述所有的卫星，则牵扯到较多的坐标系的转换计算，卫星之间解锁分离的约束方程变化不够直观。采用自然坐标描述卫星分离运动，自然坐标法能够在同一惯性系下描述所有的卫星，并可以得到表达形式简洁的系统约束方程［14］。卫星分离装置和分离策略也是卫星分离的重要研究内容。卫星之间连接分离装置可分为火工装置和非火工装置2 种类型［15］。其中，火工装置主要包括爆炸螺栓、火工锁、火工推杆等［16-18］。火工装置作用时间短，同步性高，但是其安全性差，不能够重复使用。非火工装置包括弹簧、橡胶、电磁驱动等［19-22］。非火攻装置冲击载荷小，不会造成环境污染，安全性更高［23-25］。考虑到空间安全性及减少分离后空间碎片对卫星之干扰，本文采用卫星表面附着橡胶夹层的方式完成卫星分离，并且设置初始自旋角速度［26］，以增加卫星分离的速度。

本文针对带有预紧力和柔性橡胶夹层的卫星旋转分离问题，研究了地面分离试验方案设计及支撑卫星的工装结构。建立了基于自然坐标法的分离过程动力学模型，继而对不带工装和带有工装的卫星分离过程进行了动态仿真分析，使得试验方案的合理性获得了良好的评价。基于自然坐标法建模，为在轨分离参数，如分离力、初始分离速度、卫星是否连接工装结构等对卫星分离过程的动态影响提供了分析手段。

1 分离动力学建模

1.1 分离策略设计

卫星模型简化为长方体，卫星α、β之间附着有橡胶层，旨在为2 颗卫星的分离提供分离力，如图1所示。分离前通过固定装置将2 颗卫星压紧在一起，并给予卫星一定的自旋角速度；分离时固定装置解锁，卫星通过自旋和橡胶的弹性分离力实现分离。

图1 卫星与橡胶组装Fig.1 Schematic diagram of satellites with rubber sandwich

将实验工装简化为托盘形状，如图2 所示。实验工装的作用是在地面试验时为卫星提供支撑，能够方便更换底面相同但卫星形状质量不同的多类卫星，同时减小卫星和地面实验平台之间的摩擦力。

图2 单个卫星和工装结构Fig.2 One satellite and its tooling structure

1.2 自然坐标法建模

采用自然坐标法表述2 颗卫星的位置和姿态，相比于传统的欧拉角表述刚体位姿，自然坐标法采用完全笛卡尔坐标，系统的广义坐标较为简单。此外，容易分析卫星分离系统的约束和自由度，便于写出约束方程以及约束方程的雅克比矩阵，进而能够提高仿真计算效率。

由于只研究卫星的分离策略，因此可以将卫星简化为刚体，其外形为长方体。设2 颗卫星分别为刚体α和刚体β，2 颗卫星的大小形状均相同。

自然坐标法的广义坐标为刚体上的2 个固定点，以及2 个不共面的单位向量，如图3 所示。其中，O-XYZ表示惯性坐标系，A-ςαηα ξα为固定在卫星α上的局部坐标系，单位向量uα与Aηα轴平行，单位向量vα与Aςα轴平行。

图3 卫星α 的广义坐标Fig.3 Generalized coordinates of Satellite α

卫星α的广义坐标为

如果已知位于卫星α上的任意一点P在坐标系A-ςαηα ξα中的位置矢量为rˉ，则其在惯性坐标系O-XYZ中的位置矢量为

式中：I3为3 阶单位矩阵；c1、c2、c3为局部坐标系中的i、j点的位置以及单位向量uα、vα的函数，即

同理，卫星β的广义坐标为

式中：rβi、rβj分别为固定在卫星β上的i、j点在惯性系下的位置矢量；uβ、vβ分别为固定在卫星β上的2个方向向量。

1.3 约束分析

单个刚体在空间中共有6 个自由度，使用自然坐标法描述的广义坐标含有12 个自由度，因此固有约束为6 个。以卫星α为例，设其广义坐标qα中的元素为(q1，q2，…，q12)，卫星β的广义坐标qβ的分量分别为(q13，q14，…，q24)，根据广义坐标的定义，约束方程为

式中：‖ · ‖2为向量的模；第1 式为i、j两点之间的距离约束；第2、3 式为向量uα、vα的长度，为1；第4、5、6式为向量rαi-rαj与向量uα、向量vα三者互相正交。

卫星α与卫星β的初始位置如图4 所示。

图4 卫星α 与卫星β 的局部坐标Fig.4 Local coordinates of Satellites α and β

根据图4，当卫星α与卫星β固连在一起时，固定约束可以令卫星α上的一个点与卫星β上的点重合。取该点为固连在卫星β上的局部坐标系B-ςβηβ ξβ的原点B，B点在局部坐标系B-ςβηβ ξβ上的坐标为(0，0，0)，则根据式（2），B点在全局坐标系下的位置矢量为

式中：03为3 阶零矩阵。

点B在局部坐标系A-ςαηα ξα中的坐标为(0，0，lAB)，其中lAB为A、B两点之间的距离。同样根据式（2）可以得到用广义坐标qα表示的B点在全局坐标系下的位置矢量为

根据式（6）和式（7），卫星α与卫星β之间的固定约束为

将上述约束写成分量形式，则有

由于向量rαi-rαj与向量uβ、向量vβ互相正交，向量uα与向量vβ正交，故存在3个方向的约束方程，即

同样，可将上述方程写成坐标分量的形式，即

根据以上分析可知，当卫星α和卫星β固连在一起时，一共有18 个约束方程，分别是卫星α的固有约束、卫星β的固有约束以及式（9）和式（11）所表示的两个卫星相连的固定约束。而当卫星解锁后，即2 颗卫星不在固连在一起，此时的约束方程则仅含有卫星α、β的固有约束，共12 个约束方程。

1.4 动力学模型

分析完分离前后系统的约束方程之后，结合自然坐标法的广义坐标可以得到系统的动力学方程为［26］

式中：M为系统的广义质量矩阵；q¨、q为系统的广义加速度和广义坐标；Φ(q，t)、Φq为系统的运动学约束方程及其对广义坐标的雅可比矩阵，包括刚体之间的固有约束、与刚体对应点位置矢量之间的约束以及对接完成时的位置约束；λ为拉氏乘子列阵；F(q) 为由橡胶弹性分离力引起的广义力。

本文采用广义α算法［27］求解式（12）表示的系统约束微分方程。根据虚功原理，可以得到系统的广义质量矩阵

式中：ρ0为卫星的密度；V为卫星体积。

2 地面分离动态仿真分析

2.1 不带工装情形

设单个卫星长、宽、高分别为0.3、3.0、1.5m，质量为180kg。根据图3建立局部坐标系A-ςαηα ξα。考虑到卫星内部存在很多零部件以及任务载荷，卫星并非均质，故卫星质心不位于长方体中心。假设质心位置为（1.6，-0.22，0.14）。根据其质心位置可以计算出卫星的质量惯性矩阵E1为

实验卫星分离分为两个阶段。第1 阶段，从初始时刻到3 s 时，2 颗卫星固定连接在一起，同时2颗卫星绕卫星中心以0.03 rad/s 的角速度旋转，角速度矢量方向为Y轴正方向。此时2 颗卫星之间放置橡胶，橡胶产生650 N 的预紧力加在卫星的质心上。3 s 后撤去橡胶的预紧力，此时2 颗卫星分离解锁。

根据上述自然坐标法建模编写程序，其中卫星在不同时刻的分离过程如图5 所示。可以看出，在前3 s 的时间内，卫星α和卫星β始终是一个整体，而在3 s 之后，由于卫星之间的固定装置解锁以及橡胶弹力的作用，卫星α和卫星β之间的间距越来越大，整个仿真过程并没有出现碰撞现象，表明所设计的卫星分离策略可行。

图5 不考虑工装时的卫星分离状态Fig.5 Satellite separation configurations at different moments without tooling structure

由于地面试验中，卫星只在XOZ平面内运动，因此只考虑卫星沿X轴和Z轴的运动规律。研究卫星α和卫星β上的A、B两点，用来表示卫星之间的距离变化。2 颗卫星上的A点和B点沿X轴和沿Z轴的位移变化曲线分别如图6 和图7 所示。可以看出，点A不断沿着X轴正方向运动。同样，B随着仿真时间的增加，也逐渐向X轴的正方向运动。另外，由于卫星在3 s 后分离，根据图5 给出的分离动画也可以看出，卫星β上的顶点B沿Z轴位移变化很小。

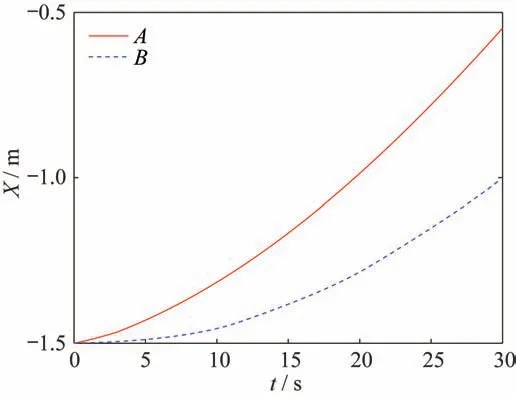
图6 点A和B沿X 轴位移变化Fig.6 Displacement variations of Points A and B along the X-axis

图7 点A、B沿Z 轴位移变化Fig.7 Displacement variations of Points A and B along the Z-axis

A、B两点之间的距离如图8 所示。可以看出，A、B两点之间的距离在3 s 之后一直呈现增大的趋势，表明在卫星解锁释放之后，卫星之间间距不断增大，说明所设计的分离策略是正确的。

图8 点A和B 之间的距离变化Fig.8 Distance variations between Points A and B

不同的初始角速度下点A和点B的距离变化曲线如图9 所示。随着自旋角速度从0.03、0.05 rad/s到0.10 rad/s 逐渐增大，A、B两点之间分离的趋势越来越大，说明随着初始自旋角速度增大，卫星之间的分离趋势也会更大，适当地增大卫星分离时的自旋角速度能够提高卫星分离的效率。

图9 不同自旋角速度下点A和B 距离变化Fig.9 Distance variations between Points A and B at different spin angular velocities

2.2 带有工装的情形

卫星工装即为卫星的底座，在仿真实验时给与卫星一定的支撑。卫星工装的形式多种多样，这里设置建立在卫星与工装组合体上的局部坐标系，如图10 所示。

图10 卫星α 及其工装结构Fig.10 Satellite α and its tooling structure

带有工装结构的卫星和不带有工装结构的卫星相比，只是在卫星的质量属性上有所变化，设置工装为铝合金材质，其密度为2 700 kg/m3，其质量变为40 kg，结合卫星的质量，可以得到单个工装和单个卫星组合体的质量为220 kg，组合体的质心位置在局部坐标系A-ςAηA ξA的坐标为(1.6，-0.4，0.15)。根据其质心位置可以计算出组合体的质量惯性矩阵E2为

分离策略与不带工装的卫星分离策略相同，即前3 s 卫星和工装组合体连在一起，同时2 颗卫星绕卫星中心以0.03 rad/s 的角速度旋转，角速度矢量方向为Y轴正方向。施加预紧的橡胶弹性力，3 s 后卫星分离。依旧使用自然坐标法建模，工装和卫星的组合体依旧使用长方体表示。得到卫星与工装的组合体在不同时刻的分离过程如图11 所示。可以看出，卫星和工装的组合体在分离过程中始终没有发生碰撞。

图11 不同时刻卫星和工装组合体状态Fig.11 Satellite separation states at different moments with tooling structures

顶点A和顶点B沿X、Z轴位移的变化如图12 和图13 所示。可以看出，卫星分离变化趋势和没有加工装的卫星基本相同，沿X轴方向的位移不断增大，沿Z轴的位移与不带工装的图6 相似。根据不带工装的位移图像对比可以得到，是否有工装对卫星分离的过程并没有太大的影响。

图12 组合体点A和B沿X 轴距离变化Fig.12 Displacement variations of Points A and B with tooling structures along the X-axis

图13 组合体点A、B沿Z 轴距离变化Fig.13 Displacement variations of Points A and B with tooling structures along the Z-axis

A、B两点之间的距离变化曲线如图14 所示。根据和图7 对比分析，当卫星加装分离的工装结构时，仅仅改变整个结构的质量特性，在几何外形上影响不大。因此，沿用原来的分离方案，对卫星和工装的组合体的分离仍然是有效的。

图14 带工装的卫星组合体上点A和B 之间的距离Fig.14 Distance variations of Points A and B with tooling structures

由上述实验的仿真结果可知，本文所设计的卫星工装结构，在连接到卫星上之后，原来所设计的卫星自旋并施加橡胶预紧力的卫星之间的分离策略仍然是可行的，设计的工装结构对卫星分离影响很小，可用于卫星分离地面实验。

3 结束语

自然坐标法可以准确地为在轨卫星分离提供仿真分析，包括不同影响因素对分离过程的影响。仿真分析结果表明：卫星之间提供弹性分离力的橡胶夹层和卫星的初始自旋角速度对卫星成功分离具有关键作用，自旋角速度越大，卫星分离时间越短。本文所设计的地面分离试验工装结构不影响卫星分离过程，在设定的转速和预紧力下，分离时卫星和工装均未发生碰撞，卫星可以成功分离。