导引头伺服机构消隙齿轮系统动力学特性分析

郑田泽，李超，朱骏，刘伟平，徐逸宇，赵倩，袁静

（1.上海理工大学 机械工程学院，上海 200093；2.上海无线电设备研究所，上海 201109）

0 引言

导引头伺服机构作为导弹伺服系统的核心部件之一，主要为微波及光学探测器提供惯性稳定平台，其性能优劣直接影响制导武器的命中精度［1-4］。由于复杂服役环境下对系统的稳定性、耐久性和传动精度要求较高，常采用双片消隙齿轮［5-7］的方式消除回程误差。由于其在工作过程中，受到时变啮合刚度、传动误差等内部激励的影响，对伺服机构的目标搜索、跟踪精度和稳定性产生较大影响。

目前，国内外已有较多学者针对消隙齿轮系统动力学特性 展开研究［8-11］。KWON等［12］以消隙齿轮传动系统为研究对象，考虑摩擦等因素，利用数值方法对其进行了动力学分析。杨政等［13］以消隙齿轮系统为研究对象，建立系统动力学模型，利用数值仿真的方法，分析了轴承预紧力等对系统频率特性的影响。廖洪波等［14］建立了消隙齿轮伺服系统的动力学模型，利用数值仿真的方法分析了静态间隙等因素对系统谐振频率的影响。刘伟平等［15］以消隙齿轮系统为研究对象，建立了考虑时变啮合刚度等因素的动力学模型，利用数值积分的方法分析了扭簧预紧力等参数对系统动态响应的影响。

上述研究中，学者们大多采用数值方法进行系统动力学响应的分析求解，但数值方法在求解此类含时变啮合刚度和间隙的强非线性系统时，存在耗时长的问题［16-18］。相较于数值求解方法，增量谐波平衡（IHB）法［19］作为一种半解析半数值方法，可以在保证计算精度的前提下，进一步提高计算效率。目前，利用IHB 法进行直齿轮、行星齿轮传动系统动力学分析的研究较多［20-25］，但尚无学者将其应用于消隙齿轮系统动力学特性的研究中。因此，本文以消隙齿轮传动系统为研究对象，建立包含时变啮合刚度、齿侧间隙和啮合误差的系统非线性动力学模型，采用IHB 法对其进行动力学响应求解，并用四阶Runge-Kutta 法进行方法有效性验证，研究了扭簧刚度、内部激励、齿轮阻尼比、轴承阻尼比等系统参数对消隙齿轮系统非线性动力学响应的影响规律。

1 消隙齿轮动力学建模

1.1 消隙齿轮传动系统工作原理

弹簧加载双片消隙齿轮结构如图1 所示。两齿轮消隙由一个固定齿轮和一个浮动齿轮同时与主动齿轮啮合传动，而且固定齿轮和浮动齿轮与主动齿轮在不同齿侧接触，达到消除齿轮反转过程中的齿隙。消隙齿轮应用过程中，为了确保齿轮啮合副能紧密贴合，通常在固定齿轮和浮动齿轮上施加预紧力，使得固定齿轮和浮动齿轮同时与主动齿轮两个不同齿侧方向的面贴合。

图1 弹簧加载双片消隙齿轮结构Fig.1 Schematic diagram of double spring-loaded anti-backlash gears

1.2 齿轮传动系统啮合刚度

根据消隙齿轮传动系统工作原理，建立如图2所示的等效刚度模型，其中，km1为主动轮和固定轮的等效啮合刚度，km2为主动轮和活动轮的等效啮合刚度，km为消隙弹簧的刚度，假设km1=km2。

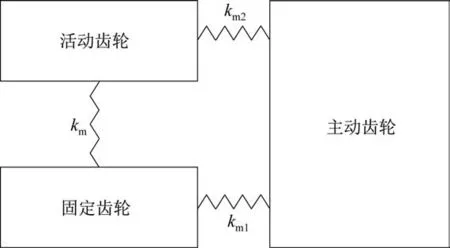
图2 消隙齿轮等效刚度模型Fig.2 Equivalent stiffness model of anti-backlash gears

间隙存在时，消隙齿轮传动系统中主动轮与固定齿轮处于分离状态，即两个齿轮之间不存在啮合刚度，此时系统仅有主动轮和活动齿轮接触，则系统的等效刚度为

间隙不存在时，消隙齿轮传动系统的主动轮同时与固定齿轮和活动齿轮接触，此时系统中固定齿轮、活动齿轮与主动齿轮之间均有啮合刚度的存在，则系统的等效刚度为

特别地，当km=0 时，消隙弹簧的作用消失，消隙齿轮传动系统变成普通的直齿轮传动系统。将式（1）和式（2）进行整理得：

1.3 模型的建立

为避免建模过程过于复杂，又能保证建模的精确性和分析精度，做如下假设：①将固定齿轮和活动齿轮作为一个整体；② 消隙齿轮传动过程中轮齿之间正常啮合，因此齿轮在反转运行的过程中，不存在回程误差；③不考虑轴承间隙的影响；④ 齿轮副啮合力的方向与啮合线方向相同。基于以上假设，结合牛顿第二定律，采用集中质量法建立消隙齿轮传动系统动力学模型，如图3 所示，关系如下：

图3 消隙齿轮副等效模型Fig.3 Equivalent model of anti-backlash gear pair

图4 间隙非线性函数Fig.4 Nonlinear function of backlash

对式（4）进行简化可得：

2 动力学响应求解方法

2.1 IHB 法推导

系统中含有非线性项，因此，需要对其做如下处理：

将式（18）和式（19）带入到式（17），在[0 2π]上进行分段积分、累加求和进行求解分析。

2.2 数值验证

为了验证本文方法的正确性，采用四阶Runge-Kutta 法进行方法验证。在齿轮啮合过程中，刚度的变化会使系统产生动态激励，是影响系统稳定性的重要参数之一。因此，分析扭簧刚度对系统动态响应的影响，仿真参数取b=1，ξ11=ξ22=0，k11=k22=0，ξ33=0.06，ξ13=ξ23=0，km=1.3，Frp=Frq=0，Fa=0.6，Fpma=0.08，Fpqe=0.03，ε=0.15，ω取［0，2.2］，得到如图5 所示的不同扭簧刚度的幅频响应。可见，随着扭簧刚度的增加，谐振频率也提高，且共振幅值呈降低趋势。系统在1.25ω处产生共振响应。如图5 所示。因此取km=2.6，分析系统在ω=1.25 的动态特性响应。在图5 和图6 中，“∘”为Runge-Kutta 法，“-”为IHB 法。通过对比可以看出，2 种方法所求结果相吻合，如图6 所示。

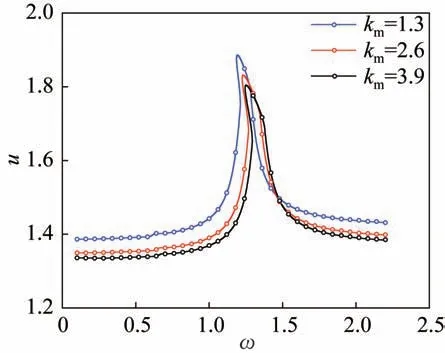
图5 不同扭簧刚度的幅频曲线Fig.5 Amplitude-frequency curves of different torsion spring stiffness

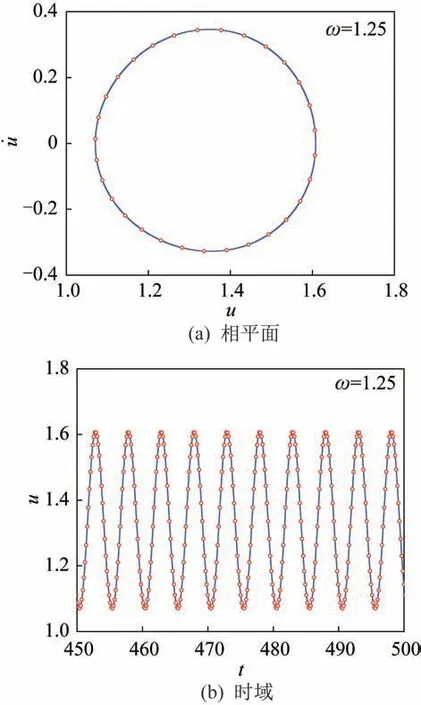
图6 扭簧刚度km为2.6 时系统的动态响应曲线Fig.6 Dynamic response curves when km=2.6

3 消隙齿轮动力学特性分析

采用上述IHB 法求解系统的动力学响应，通过数值仿真分析得到系统的时域曲线、频谱图、相平面图、庞加莱截面图、分岔图等，研究消隙齿轮传动系统动力学特性，分别研究了内部激励、齿轮阻尼比、轴承阻尼比等参数对系统动态特性的影响规律。

3.1 内部激励

齿轮系统在运动过程中，由于制造装配、刚度的不断变化，导致齿轮啮合副产生内部激励。即使外部激励是常值，也会因轮齿啮合位置及齿数的周期性变化使系统内部产生动态激励，甚至产生共振现象。因此，采用控制单一变量的方法，控制其他参数不变，取b=1，ξ11=ξ22=0，ξ13=ξ23=0.01，ξ33=0.06，k11=k22=1.05，km=1.3，Frp=Frq=0，Fa=0.6，Fpma=0.08，ε=0.15，ω=0.8，通过改变内部激励的大小，分析其对齿轮系统动态特性的影响，得到如图7 所示的基于内部激励Fpqe在区间［0，0.8］的分岔图。由图7 可以看出，随着内部激励的增加，系统由倍周期运动逐渐变为混沌运动。

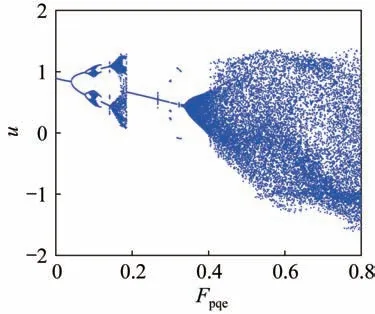
图7 基于内部激励的Fpqe的u 向分岔Fig.7 Bifurcation of Fpqe based on internal excitation in the u-direction

为了进一步分析内部激励对系统周期运动动态响应的影响，分别取内部激励Fpqe为0.038、0.058、0.078 和0.098 几种情况进行分析，得到系统的相平面图、庞加莱截面图、时域曲线和频谱图等，分别如图8～图11 所示。

图9 内部激励Fpqe为0.058 时动态响应曲线Fig.9 Dynamic response curves when Fpqe=0.058

图10 内部激励Fpqe为0.078 时动态响应曲线Fig.10 Dynamic response curves when Fpqe=0.078

图11 内部激励Fpqe为0.098 时动态响应曲线Fig.11 Dynamic response curves when Fpqe=0.098

由图8～图11 可以看出，随着内部激励的增加，系统由倍周期运动变为混沌运动，且共振幅值呈增大趋势。可见，如果齿轮内部激励比较大，系统出现混沌状态，此时齿轮啮合容易出现撞击，甚至脱齿的现象，当齿轮内部激励比较小时，系统处于收敛状态，此时系统仅有齿面激励。

3.2 齿轮啮合副阻尼比

研究齿轮啮合阻尼比对系统动力学特性的影响，分别取b=1，ξ11=ξ22=0，ξ13=ξ23=0.01，k11=k22=1.05，km=1.3，Frp=Frq=0，Fa=0.6，Fpma=0.08，Fpqe=0.08，ε=0.15，ω=0.8，齿轮啮合副阻尼比ξ33在［0，0.1］之间的动态响应。如图12 所示，通过分岔图分析齿轮啮合阻尼比在一定范围内对系统动态特性的影响。通过图12 可以看出，随着齿轮啮合阻尼比的不断增大，齿轮传动系统由混沌运动逐渐变为4 倍周期、2 倍周期，直至最后变为1 倍周期运动。

为分析齿轮啮合阻尼比对系统周期运动动态响应的影响，控制其他参数不变，仅改变齿轮传动系统的齿轮啮合阻尼比，分别取ξ33为0.02、0.04、0.06 和0.08 几种情况进行分析，得到系统的相平面图、庞加莱截面图、时域曲线和频谱图等，分别如图13～图16 所示。

图13 齿轮啮合阻尼比ξ33为0.02 时动态响应曲线Fig.13 Dynamic response curves when ξ33=0.02

图14 齿轮啮合阻尼比ξ33为0.04 时动态响应曲线Fig.14 Dynamic response curves when ξ33=0.04

图15 齿轮啮合阻尼比ξ33为0.06 时动态响应曲线Fig.15 Dynamic response curves when ξ33=0.06

图16 齿轮啮合阻尼比ξ33为0.08 时动态响应曲线Fig.16 Dynamic response curves when ξ33=0.08

由图13～图16 可知，随着阻尼比的增加，系统由混沌运动逐渐变为倍周期运动，且振动幅值减小。可见，如果齿轮啮合阻尼比较小，系统会出现齿背激励，当啮合阻尼比较大时，系统逐渐收敛，齿背激励逐渐消失，仅有齿面激励。因此，通过改变阻尼比的大小，对减少系统的冲击和降低振动幅值具有重要的影响。

3.3 轴承阻尼比

进一步分析轴承阻尼比对系统的动态特性的影响，改变轴承阻尼比的大小，控制其他参数不变，取b=1，ξ11=ξ22=0.01，ξ13=ξ23=0.01，ξ33=0.06，k11=k22=1.05，km=1.3，Frp=Frq=0，Fa=0.6，Fpma=0.08，ε=0.15，ω=0.8，通过分岔图分析轴承阻尼比在一定范围内对系统动态特性影响。轴承阻尼比ξ11=ξ22在［0，0.05］之间的动态响应，如图17 所示。

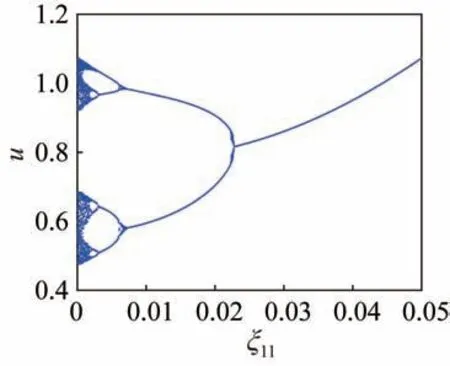
图17 基于轴承支承阻尼比ξ11和ξ22的u 向分岔Fig.17 Bifurcation based on ξ11 and ξ22 in the u-direction

通过图17 可以看出，随着轴承阻尼比的增大，齿轮传动系统由混沌运动变为4 倍周期、2 倍周期，1 倍周期运动。为了进一步分析轴承阻尼比对系统周期运动动态响应的影响，分别取ξ11=ξ22为0、0.065、0.018 5 和0.030 5 几种情况进行分析，得到系统的相平面图、庞加莱截面图、时域曲线和频谱图，分别如图18～图21 所示。

图18 轴承支承阻尼比ξ11和ξ22为0 时动态响应曲线Fig.18 Dynamic response curves when ξ11=ξ22=0

图19 轴承支承阻尼比ξ11=ξ22=0.065 时动态特性曲线Fig.19 Dynamic response curves when ξ11=ξ22=0.065

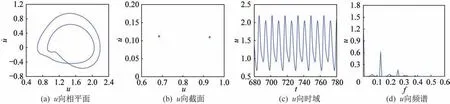
图20 轴承支承阻尼比ξ11和ξ22为0.018 5 时动态响应曲线Fig.20 Dynamic response curves when ξ11=ξ22=0.018 5

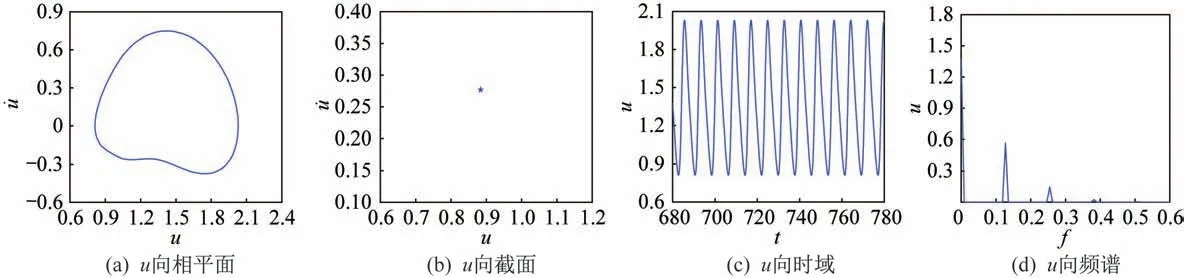
图21 轴承支承阻尼比ξ11和ξ22为0.030 5 时动态响应曲线Fig.21 Dynamic response curves when ξ11=ξ22=0.030 5

图18 中，当ξ11=ξ22=0 时，此 时系统为 混沌运动，u向具有明显的基频和倍频。通过对比图18～图21 的动态响应曲线，从相平面图和庞加莱截面图中可以看出，轴承阻尼比与齿轮啮合阻尼比对系统的影响规律类似，即随着轴承阻尼比的增大，系统由混沌运动逐渐变为4 周期运动、2 周期运动，直至1 周期运动，且振动幅值减小。因此，如果轴承阻尼比较小，系统容易出现轮齿啮合之间的碰撞等现象，随着轴承阻尼比的不断增大，系统逐渐由混沌变为收敛。从收敛时间来看，随着轴承阻尼比的增加，系统转变为周期运动时间减小，即收敛速度变快。其次，从时域图和频谱图中可以看出，随着轴承阻尼比的增加，系统的共振幅值减小，均有基频和倍频出现。综上可知，阻尼比的不断降低，会造成系统倍周期分岔，最后使齿轮系统进入混沌运动。因此，通过改变轴承阻尼比的大小，对提高系统收敛速度、减少系统冲击和降低共振幅值具有较为重要的影响。

4 结束语

本文以消隙齿轮系统为研究对象，建立考虑时变啮合刚度的归一化动力学模型；采用IHB 法进行系统动力学响应求解，并利用四阶Runge-Kutta 法进行验证，研究了扭簧刚度、内部激励、阻尼比等参数对系统动力学响应的影响规律，所得结论如下：

1）分析扭簧刚度对谐振频率和系统稳定性的影响，随着扭簧刚度的提高，系统谐振频率也提高，且共振幅值降低；

2）分析内部激励、齿轮啮合阻尼比、轴承阻尼比等参数对齿轮系统稳定性的影响，随着内部激励的增加，系统由周期运动逐渐变为混沌运动，且振幅随着激励的增加而增加；随着阻尼比的增大，系统由混沌运动逐渐变为周期运动，且振幅减小。

3）在实际工程应用中，通过提高扭簧刚度、阻尼比，降低内部激励幅值等参数，对提高系统稳定性、减少冲击和降低共振幅值具有一定的指导作用。