构架式天线柔性动力学建模与展开精度分析

秦远田，张子昊，朴丽花

（南京航空航天大学 航天学院，江苏 南京 210016）

0 引言

随着卫星移动终端不断向轻量化、便携化方向发展，以及对空间时间敏感目标检测日益增长的需求，大型空间可展开天线逐渐成为满足卫星高轨移动通信和遥感要求的关键技术载荷［1］。根据相关文献表明，大规模空间天线的信号增益以及有效传播距离与天线孔径直接呈正相关［2］。为提高航天器结构的技术指标，空间天线的规模趋于增加，其机械结构也更加复杂。在此需求的推动下，构架式可展开天线系统应运而生。尽管许多大型空间展开天线已经成功发射［3-5］且能够顺利展开，但是天线及其反射面在展开过程中，仍然存在诸多未解决的问题［6-7］。经过各国研究人员对大型空间展开天线及其动力学特性的研究与求证，得出的结论是动力学建模低成本研究空间天线不可或缺的工具［8］。

在可展开天线柔性动力学的研究领域，常见方法有诸如运动弹性动力学（Kineto-Elasto-Dynamic Analysis，KED）［9］、浮动坐标法以及模态分析方法等［10］，其中绝对节点坐标法方法（Absolute Nodal Coordinate Formulation，ANCF）由SHABANA［11］于1996 年提出。ANCF 建模依赖恒定质量矩阵，没有考虑离心力或是Coriolis 力，适用于描述柔性体的刚性运动。该方法被认为是多体系统动力学研究史上最重要的进展之一。由于国内对绝对节点坐标法的研究应用起步较晚［11］，ANCF方法仍在大型天线展开动力学领域有很大的研究空间以及良好的应用前景。相关研究有诸如易乐天等［12］将ANCF 方法用于分析缠绕肋天线的展开过程，LU等［13］基于ANCF方法对周边环形可展开天线进行了一系列研究，但是目前ANCF 方法在构架式可展开天线方面的应用很少。因此，本文对构架式天线的柔性多体动力学建模与分析方法具有实际应用价值。

本文在对构架式展开天线进行无铰链间隙的多刚体动力学数值分析时，发现在天线展开后期，天线基本单元各关节的加速度陡增。通过ADAMS 动力学软件进行地面试验模拟来对比数值分析结果，如图1 所示。图中，杆件1、2 为动力学仿真建立的虚拟吊挂系统。图中可见，在虚拟吊挂牵引的天线基本单元末端关节处，以及虚拟吊挂系统与天线基本单元的连接处，同样出现了关节横向展开力异常增大的现象，以至于该动力学分析的结果难以指导地面试验的进行，见表1。

图1 构架式展开天线地面试验模拟过程（基本单元）Fig.1 Ground test simulation of a deployable truss antenna（basic unit）

表1 弹簧驱动力与末端关节展开力关系Tab.1 Relationship between the spring driving force and the deploying force for the end joint

由表1 可知，天线杆件两铰接点之间的几何尺寸在天线展开过程中并非一成不变，因此需要引入铰链间隙。然而，该型构架式多模块天线存在近500 个铰链关节，并且铰链间隙的接触建模存在很强的非线性。不仅含间隙的多刚体动力学数值分析方法难以进行，动力学仿真软件同样无法处理数量庞大的间隙接触问题。由于构架式天线的结构与材料刚性较强，展开过程中的微小形变不会影响天线展开过程的顺畅性。因此，为了避免直接处理具有强非线性的铰链间隙问题，本文采用了柔性多体动力学方法。通过引入弹性项，希望能够将影响天线顺利展开的铰链间隙问题转换为天线杆件的微小形变，从而得到接近天线真实展开情况的动力学参数，并为后续地面试验提供理论指导。

1 柔性多体动力学建模

构架式可展开天线作为一种可折展的多模块天线，其反射面结构多为可折叠桁架，金属网铺设在骨架上。这类天线骨架组成如图2（a）所示，整个天线反射器由7 个模块组成，呈中心对称分布。每个模块包含6 个基本的结构单元构成，为使得桁架能够达到折叠的效果，桁架的杆件中间设有铰链，并通过弹簧机构驱动天线展开。如图2（b）所示，本文所述天线的单模块模型，在中心竖杆上设有的弹簧机构，通过释放压缩弹簧，使弹簧两端的滑块进行向竖杆上端移动。利用曲柄滑块机构（由图2（b）中2、3 和7 组成）带动单个模块内所有结构单元进行横向展开，并在滑块移动一定距离后，实现机构自锁。在整个展开过程中，导致空间天线系统展开失败的原因有很多［14］，其中该过程中的动力学建模不准确是一个重要因素。天线完全展开的过程，不仅涉及空间刚体大尺度运动和弹性小变形的耦合运动，还涉及线性和非线性的耦合。此外在反射器的运动模块内，采用细长杆件在展开过程中出现一定的弹性变形。很多天线设计与运动学建模的研究，将所有杆件完全视为刚体，从而忽视了其对天线展开后型面精度的影响，以至于天线展开失败或者未能达到预计的工作效果。

图2 构架式展开天线结构组成与展开原理Fig.2 Structural composition and deploying principle of the deployable truss antenna

1.1 基于构架式天线的改进梁单元建模

本节建立了构架式可展开天线桁架系统的动力学模型。由于所述模块化展开天线结构复杂，因此需要对模型进行简化。由于所述天线结构在几何分布上具备同构性，故仅需对其结构单元的桁架系统进行动力学建模。根据SHABANA 和YAKOUB 提出的ANCF 方法［15］，对于一个三维的二节点梁单元模型，长度为L，共有如下24 个绝对坐标：

然而采用绝对坐标法对复杂的天线桁架结构进行分析，最终得到的刚度矩阵膨胀非常严重。为提高单元的计算效率，将节点的广义坐标改为一个位置向量和一个对梁轴线X进行微分得到的梯度向量。因此其位移场可以简化为

为了避免大变形与小变形问题中的锁定现象，上述降阶的方法消除了表示扭转效应的绝对坐标。根据构架式可展开天线的结构特点，以及杆件采用的碳纤维复合材料所具备的优良属性，本文认为天线展开以及型面精度问题的主要研究对象为弹性拉伸和弯曲效应。为进一步提高计算效率，通过消除运动方程中剪切效应的刚性项，重新构建适用于上述低阶广义坐标的形函数为

式中：xi为梁轴线上的相对坐标值。

基于广义坐标的改变，质量矩阵可以通过关于xi的积分进行计算：

式中：A为梁单元横截面面积；ρ为密度。

假定梁单元横向抗弯刚度相同，根据Euler-Bernoulli 梁公式可知，梁单元内力的虚功表示为

式中：E为弹性模量；I为截面惯 性矩；κ为轴线曲率，其表达式可由Seret-Frenet框架［16］进行推导；εa为轴向应变，根据Green 应变张量［16］确定。

κ与εa推导结果如下：

上述计算弹性力的方法，在处理复杂系统时会出现累积误差，甚至是不收敛的情况。因此需要采用Piola-Kirchhoff 应力张量推导出固定的弹性力的Jacobi 矩阵来修正上述方法［17］。对于天线模块的结构单元，其弹簧驱动装置通过释放压缩弹簧提供外力，故整个天线反射器的弹性势能与弹簧阻尼虚功为

式中：n为天线模块数量；l0为未压缩状态下弹簧位置矢量；rp为弹簧力作用点的位置矢量；k、c分别为弹簧刚度系数和阻尼系数。

由于空间微重力环境的特点，天线在展开状态下重力近似为0。故广义外力表示为

式中：F为作用在rp处的外力。

1.2 天线桁架系统的约束方程

天线反射器的动力学模型主要包括3 种约束，即受弹簧驱动的滑块运动、杆件之间的铰接约束以及杆件的刚性连接。所述天线模块内的滑块属于柱形接头模型［18］，主要限制了滑块沿杆件径向的自由度。假定轨道记作物体m，滑块记作物体n，在连接点a处两者时刻保持接触。约束方程为

式中：sm为滑块在物体m上位移的距离；为物体m上滑块的初始坐标；为物体n上连接点a的坐标；vn为物体n上在连接点a处的矢量，方向沿柱形接头横截环面的中心轴线方向分别为物体m、n的中心轴线方法向量。

为进一步限制滑块接头沿物体m转动的自由度，需要增加约束方程为

旋转铰接约束是球形铰接的一种特殊情况，在进行球形铰接约束时，只需保证两物体端点在连接点位置矢量相等而不约束转动方向，即：

对于所述天线反射器模型，为保证模块间不会发生纠缠，旋转关节只允许一个自由度的相对转动。由天线单模块结构特性可知，其中心杆与所有结构单元的旋转关节的轴线方向始终保持垂直。假定天线单模块的中心杆轴线的方向矢量为vc，物体m和n在旋转铰接点a处的分别沿关节轴线方向定义矢量为，旋转铰接点的约束方程如下：

由于ANCF 方法建立的是一般Euler-Bernoulli梁单元模型，而所研究的构架式可展开天线模型具有很强的结构非线性。

为消除非线性带来的影响，需要对复杂杆件进行拆分，并通过刚性连接的方式进行约束。该刚性连接消除了所有相对平移与旋转的自由度，其约束方程表示为

由于天线结构单元结构十分复杂，且杆件之间尺寸差距大，直接对整个结构单元进行动力学并行求解会导致矩阵条件数过大，从而影响求解精度或是出现动力刚化的现象。因此需要对结构单元拆分，运用模块前向链式法求解。通过前行模块动力学的解来不断更新后续模块的基准位置矢量与广义力，能够很好地减少计算累积误差。模块按照颜色划分求解顺序如图3 所示。

图3 基本单元内拆分模块的求解顺序Fig.3 Solving order of the split blocks in the antenna basic units

1.3 天线多模块扩展

由于单个模块内的6 个天线结构单元和7 个天线模块分别呈中心对称且分布均匀，多模块天线俯视图如图4 所示。以图示坐标系为全局坐标系（右手系），天线结构单元i上任意一点k在全局坐标系下的位置向量rk为

图4 多模块天线示意图（俯视图）Fig.4 Diagram of the multi-modular antenna（top view）

假定天线展开过程中，模块间的夹角不变，则两模块之间的位置关系可通过4 个天线结构单元来确定，如图5 所示。

图5 模块间的位置关系Fig.5 Position relationship between two modules

根据图5（a）中几何关系，通过将两模块连接节点的广义坐标进行叠加并归一化，可以得到平面GH的单位法向量。若存在空间内点M、N的广义坐标为eM、eN，且其前3 项元素组成的时变矢量表示为e(x，y，z，t)，则有：

假定模块1 位于多模块天线的中心位置，其中心杆为O1P1且本体坐标系x1y1z1，P1K和P1K为两中心杆的轴线延长线，如图5（b）所示。模块2 为与模块1 连接的周边模块之一，中心杆为O2P2且本体坐标系x2y2z2，则周边模块的本体坐标系在全局坐标系下位置关系推导为

式中：vz1为中天线模块本体坐标系z1轴的方向向量。

根据天线结构结构单元的特性，可知：

式中：es(x1，y1，z1，t)和eu(x1，y1，z1，t)分别为中心模块天线结构单元中，即图5（b）所示O1H或O1G位置上的结构单元中的侧杆与上肋杆对应的位置矢量，方向指向点H。

O1O2连线的位置矢量为

若以中心模块的本体坐标系为全局坐标系，则周边任意一个本体坐标系下的广义坐标为eBS的天线模块，在全局坐标系下的坐标eGS为

1.4 动力学模型求解

绝对节点坐标法的动力学求解方程［19］为

式中：Q为外部施加的作用力、惯性力以及由变形产生的弹性力；Qc为由于单元之间连接所产生的约束力。

基于所研究天线基本单元的多体动力学系统存在上述各种约束关系，故而系统广义坐标不独立。利用相关动力学原理［17］，通过约束方程对时间进行二次求导，使其变为时变量，并引入Lagrange第一类方程进一步得到以下微分代数方程为

式中：Φq为约束方程的Jacobian 矩阵；λ为Lagrange乘子；C(e，t)为约束条件的代数方程组；Ce(e，t)为C(e，t)对广义坐标向量求一阶偏导数。

为避免求解发散的情况，对上述柔性多体动力学方程组进一步改进。本文采用Baumgarte 提出的一种基于控制反馈策略的约束稳定性方法［20］，即在解中引入稳定性系数，得到如下形式：

式中：Φ为代约束方程关于时间的二阶导数部分；α和β为稳定因子，其选取方式参考相关文献［21］。

通过模块前向链式方法对结构单元拆分求解，并将式（23）和式（26）联立，可以得到多模块构架式可展开天线中所有节点的位置矢量、速度与加速度信息。最终采用Newmark 方法对上述动力学方程进行求解。

2 多模块天线展开精度分析

2.1 动力学模型验证

由于所研究多模块天线有近千个节点与梁单元，不便对每个节点的位移、速度加速度进行验证说明。因此本文采用能量法［22］对所述天线的柔性多体动力学模型的准确性进行验证。单元体的应变能与势能已分别在式（8）和式（10）中进行了描述，根据建立的动力学关系，对于任意梁单元上的任意点S，其在全局坐标系x1y1z1下的位置矢量为rS进行线性积分得到的动能表达式为

因此对于多模块天线系统的动能表达式为

式中：Tj为铰接点的动能。

构架式天线展开过程较为缓慢，可将铰链关节的阻尼近似视作黏性阻尼，并与展开角速度成正比。根据Rayleigh 耗散公式［23］，系统耗散能为

式中：ζ为黏性摩擦系数为关节转动角速度。

天线杆件的主要材料采用碳纤维增强树脂基（环氧树脂）复合材料，其材料属性设置见表2。

表2 天线杆件材料属性Tab.2 Material properties of the antenna rods

以单模块天线为例，本文通过上述方程对天线系统能量进行求解，得到仿真结果如图6 所示。

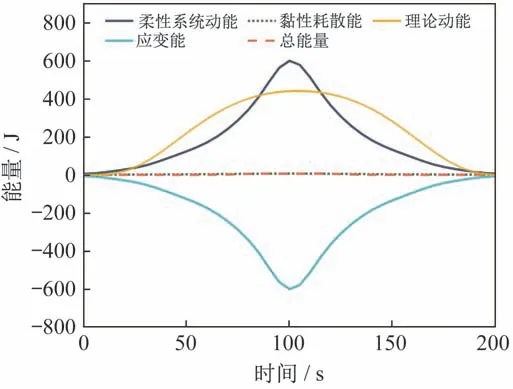
图6 系统能量变化曲线Fig.6 Curves of system energy over time

本文得到的整个天线展开过程持续210 s 左右。由于单模块天线在展开过程中的弹性势能首先转化并存储在曲柄滑块机构中，作为应变能的形式引起结构的变形。期间损耗的弹性势能很小，故未在图6 中表示出。再由应变能驱动滑块移动，从而导致动能的增加与后续结构的弹性变形。在天线展开后期，为避免出现由于展开速度过大而导致天线结构受到巨大冲击的问题，本文通过绳索控制弹簧的展开速度，将天线展开过程中的动能耗散，保证天线能够缓慢、平稳地展开到预定型面。整个过程，包含耗散的能量和弹簧阻尼做的功，总能量保持趋近于零，从而通过能量守恒证明了本文柔性多体动力学仿真结果的可靠性。此外，图中标注了根据能量守恒与弹簧机构行程变化得到的系统理论动能，并与柔性系统动能进行比较。由于弹性变形导致的结构振动和弹性动量矩会产生额外的动能［24］，并且天线所有动能都来自弹簧展开机构，即总动能近似相等。因此本文建立的柔性多体动力学模型符合真实的天线展开情况。

2.2 天线展开动力学结果分析

在天线的动力学模型得到验证以后，为直观展示天线展开进度与展开过程的顺畅程度，在图4 中选取中心模块与周边模块2、3 的连接点为分析对象。其在x、y平面内的径向位移、速度、加速度以及径向展开力的结果如图7 所示。

图7 天线展开动力学参数随时间变化曲线Fig.7 Cureves of the antenna deploying dynamics parameters over time

续图7 天线展开动力学参数随时间变化曲线Continuoued Fig.7 Cureves of the antenna deploying dynamics parameters over time

在展开过程中，多模块天线周边的基本单元展开基本不受影响，而在模块间连接点上的径向展开力，可能会影响天线展开的顺畅程度。上述结果旨在表现天线展开过程中，在x、y平面上中心模块包络变化的过程。前文所述模块末端关节力的位置与方向等同于上述径向展开力。可以看出：相较于整个展开运动顺畅且平稳；相较于未包含铰链间隙的刚体动力学仿真结果，模块末端关节力的结果更加贴切真实情况。两种动力学建模方法下的模块间连接点的径向展开力进一步比较如图8 所示。

图8 两种建模方法下的天线模块末端节点上的径向展开力随时间变化曲线Fig.8 Radial unfolding force at the end node of the antenna module over time under two modeling methods

如图8 所示，同比减少率=（未含铰链间隙的刚体动力学计算结果-柔性体动力学计算结果）÷未含铰链间隙的刚体动力学计算结果×100%。未含铰链间隙的刚体动力学计算结果，在展开初期与柔性体动力学计算的结果差距很小。但随着天线的展开，两者差距逐渐加大。在展开完成时（即横坐标为220 s 的条形图），两者的天线模块间的径向展开力相差约106倍。说明该型构架式天线在忽略铰链间隙的情况下，动力学理论分析的结果无法指导地面试验的进行。然而如果引入数量庞大且非线性强的铰链接触模型，多模块天线展开动力学的理论分析又难以顺利进行。因此本文提供了另外一种思路，即上述柔性多体动力学建模方法。该方法能够在避免处理众多铰链间隙模型的情况下，查验天线的展开运动情况。此外，由于大型天线的展开过程十分平缓，需要确保在其展开过程中的卫星姿态与振动不会影响天线展开的顺畅性［25-26］。该方法得到的刚度矩阵与质量矩阵，能够为研究构架式天线展开过程中的结构动力学问题奠定基础。

2.3 天线展开型面精度分析

为抵消铰链间隙的影响，本文采用柔性动力学的分析方法，因此得到的展开后天线结构的形变一定会大于实际情况。如果形变结果严重影响了最终天线的型面精度，则说明本文所采用的简化方法不具备参考意义。因此需要进一步确认该模型下得到的天线型面是否符合设计期望。

由于多模块构架式天线的几何组成特点，可将天线拆成基本单元来对比观察本文得到的柔性体模型与期望型面下的模型之间的形变误差影响，如图9（a）所示。可以看出，虽然天线基本单元上的杆件在Y轴方向有较大形变误差，但作为天线型面所需要的关键点下端的中心杆与侧杆形变误差很小。放大到天线单个模块的模型中观察，如图9（b）所示，可以发现单模块天线柔性体模型最终的展开完成度较高，基本不存在因形变误差产生的卡顿与位置偏差问题。该结果进一步说明本文采用的无铰链间隙的柔性体动力学分析方法能够消除铰链间隙模型对动力学分析的影响。

图9 柔性体模型的形变误差分析Fig.9 Deformation error analysis of the flexible model

为进一步研究本文采用柔性体模型的形变误差对七模块构架式天线的整体型面精度的影响，通过观察七模块天线柔性体模型的拟合形面，如图10 所示，可发现在x、y平面上的等高线图分布较为均匀。说明不仅单个模块的展开完成度高，各个模块之间也不存在局部展开不到位的情况，即本文采用的柔性动力学方法在增加模块的情况下仍然适用。

图10 多模块天线桁架系统柔性体模型的拟合型面Fig.10 Fitting profile of the flexible model for the multimodule antenna truss system

此外，通过比较七模块天线桁架系统与期望模型的均方差（Root Mean Square，RMS）误差值，得到如图11 所示的多模块型面精度误差情况。

图11 多模块天线桁架系统的型面精度分析Fig.11 Profile accuracy analysis of the multi-modular antenna truss system

根据计算结果可知，整个多模块柔性体模型相较于期望模型的RMS 误差值为0.013 641 mm。对不同的关键点的型面精度误差，最小的仅8.962 8×10-5mm，最大的接近0.04 mm。如图11（b）所示，中心模块关键点上的型面精度误差最小，最大的型面精度误差主要集中在多模块天线周边的关键点上。

这说明本文采用柔性动力学方法来处理多模块构架式展开天线，虽然能够解决刚体动力学方法难以处理大量铰链间隙非线性的问题，但在用结构弹性形变抵消铰链间隙影响的同时，柔性体模型产生的形变误差最终会对天线的型面精度产生一定程度的影响。然而这种形变误差对天线形面精度的影响很小且可被估计。因此，本文的柔性多体动力学建模方法对构架式天线的设计与制造有实际参考意义。

3 结束语

本文为解决构架式多模块可展开天线的刚体动力学模型需要引入铰链间隙，却又因铰链非线性强、数量过大而导致难以求解的问题。通过将铰链间隙的影响转化为弹性形变误差的方法，对构架式模块化可展开天线进行了柔性多体动力学建模。基于绝对节点坐标法对单个杆件进行柔性梁单元建模，并采用了改进的梁单元模型来提高单元计算效率，减少计算过程中的矩阵膨胀。通过消除形函数的刚性项，避免计算时出现锁定的问题。通过对复杂桁架系统进行模块拆分和链式运算，引入稳定系数与调整计算策略等方法，最终建立了含约束方程的柔性多体动力学模型。

通过天线结构的几何关系，建立了多模块动力学模型。本文通过能量法，验证了复杂桁架系统动力学模型的准确性，最终得到了天线模块间径向展开的动力学特性。本文对刚柔2 种动力学模型在同一位置的径向展开力进行对比分析，说明了所建立的柔性动力学模型更加贴近实际情况，并且采用的无铰链间隙的柔性体动力学分析方法能够消除铰链间隙模型对动力学分析的影响。此外，得到的刚度矩阵与质量矩阵，能够为研究构架式天线展开过程中的结构动力学问题奠定基础［26］。通过分析天线展开后的型面精度情况，说明在用结构弹性形变抵消铰链间隙影响时，柔性体模型产生的形变误差最终会对天线的型面精度产生了很小且可被估计的误差。