导引头伺服系统预定回路滑模控制律设计
2023-05-12赵明翰张艳赵桂军周鲁包旭馨
赵明翰,张艳,赵桂军,周鲁,包旭馨
(1.上海无线电设备研究所,上海 201109;2.海军装备部驻上海地区第六军事代表室,上海 201109)
0 引言
随着信息化与控制技术的快速发展,现代化武器对于导引头精度提出了更高的要求[1-2]。对于现代化导弹而言,其精度除了受到制导律及其固有结构特性的影响外,很大程度上受到导引头视线角指向精度的影响。传统的导引头伺服系统控制律设计大多采用线性方法,其优点在于设计简单,调试方便,但由于在设计线性控制器的过程中对于模型进行了一定程度的简化,所以在实际应用的过程中按照传统线性方法设计的控制律并不能获得理想的控制效果。因此,需要考虑使用其他方法设计控制律来满足导引头系统的高精度控制需求。
在导引头工作的过程中,主要存在3 个工作状态:预定回路、稳定回路和跟踪回路[3-4]。对于预定回路而言,其主要任务是完成导引头天线的一个固定指向,使导弹在发射后能够快速捕获目标回波信号,减小搜索目标时间。基于此,在设计控制律的过程中需要满足快速性以及稳态误差的要求,尽可能保证系统快速到达且稳态误差越小越好。传统的设计方法大多采用线性超前滞后的方法或者是PID 方法进行设计,这种方法设计的控制律在实际系统中由于各种非线性环节的存在导致效果并不理想。针对这些问题,文献[5]使用自抗扰算法抑制非线性环节对于系统的影响,文献[6-7]使用单神经元对相关控制算法优化了预定回路的过渡过程,文献[8-10]使用自适应模糊PID算法来进行优化,均取得了一定的效果。除了优化控制算法外,针对永磁电机的控制,文献[11-13]进行了相关的优化设计,也从一定程度上优化了整体系统的性能。
滑模控制理论是由苏联学者在20 世纪50 年代提出的变结构控制理论,通过系统状态偏离切换面的不同情况来切换控制器的结构实现控制任务,通过切换不同的控制器来实现快速性与小稳态误差并存的控制效果。
1 系统建模
对于导引头系统预定回路而言,其基本工作原理框图如图1 所示。图中:θ˙为角速度;θ为角速度积分后得到的角度。
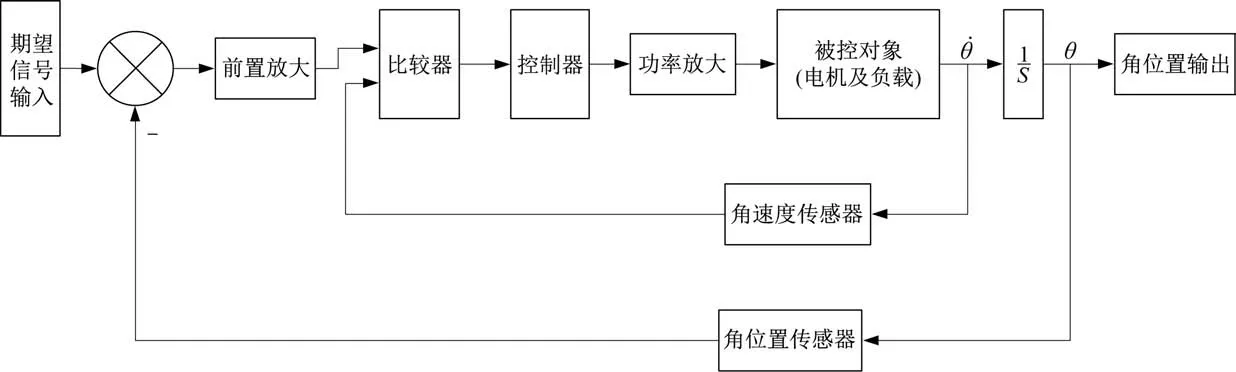
图1 预定回路原理框Fig.1 Schematic diagram of predetermined loop
由图1 可知,前置放大环节由一个比例环节加一个饱和非线性环节组成,功率放大部分由一个饱和非线性环节和一个比例环节构成,被控对象部分由电机和负载组成,其动力学方程为
式中:J为被控对象部分的转动惯量;TM为电机的输出转矩;Tc为系统中的干扰力矩。
由于系统中的电机选用的是直流电机,对于直流电机而言,式(2)中的方程是描述其动态特性的基本方程:
式中:Tem为电磁转矩;Kt为转矩系数;Ia为电枢电流,A;Ea为电枢反电势;Ke为反电势系数;ω为电机转子的角速度;Ua为电枢两端输入电压;La为电枢电感;Ra为电枢电阻。
对式(2)中的时域方程进行零初始条件的拉普拉斯变换,可以得到:
式中:s为拉普拉斯算子;Ω为电机角速度。
对于式(3),其中的干扰力矩Tc主要由摩擦、死区、间隙等典型非线性环节导致,在处理的过程中,将这部分干扰力矩单独提出,作为整体传递函数中的非线性环节。将剩余的环节线性化后可以得到以角速度为输出量,电压为输入量的直流电动机传递函数:
由于选用的直流电动机电磁时间常数远小于机械时间常数,所以可以对式(4)进行适当的简化,简化后的传递函数为
由于被控对象中的非线性主要由死区特性导致,其他非线性环节影响有限,可以忽略,所以,最终得到的被控对象部分由一个死区非线性环节和一个惯性环节组成。
对于角位置传感器和角速度传感器,由于其存在的时间滞后系数较小,因此可以近似为一个比例环节进行处理。综上所述,参照实际元器件参数得到的框图如图2 所示。图中:Gain 为比例增益环节;K为惯性环节传递函数增益;T为惯性环节传递函数时常数;为角速度;θ为角速度积分后得到的角度。
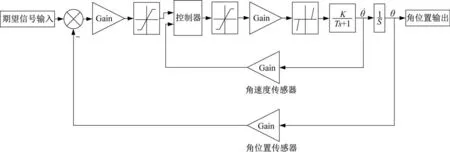
图2 控制回路实际框Fig.2 Actual block diagram of the control loop
最终得到的系统前向通道线性部分的传递函数为
2 滑模控制律设计
针对式(6)中得到的前向通道线性传递函数,可以设计基于趋近律的滑模鲁棒控制器。滑模函数设计为[14]
其中,c>0满足Hurwitz条件。误差及误差的导数为
式中:θd(t)为理想角位置信号;(t)为当前角位置信号。
则有:
采用指数趋近律,有:
式中:ε为指数趋近律中等速趋近部分的系数(ε越小,趋近速度越慢;ε越大,趋近速度越快,到达切换面时的速度也越快,引起的抖振也越大);k为数趋近律中指数趋近部分的系数(k越大,速度衰减越快;k越小,速度衰减越慢)。
因此,在选择指数趋近律系数的过程中,为了在保证系统误差快速收敛的同时减小系统在切换面附近的抖振问题,需要适当选择ε和k的值。通过式(9)和式(10),得:
则滑模控制律为
式中:c为一个系数,用于产生由于角速度偏差生成的控制量。
对于设计好的滑模控制律式(12),绘制系统线性部分的Bode 图,如图3 所示。通过Bode 图可以看出,对于系统的线性部分而言,系统的相角裕度约为75.3°,具有较好的稳定裕度,但由于未考虑系统中的非线性部分,所以对于整体包含非线性环节的系统的稳定性尚不确定,需要进一步研究。

图3 滑模控制系统的Bode图Fig.3 Bode diagram of the sliding mode control system
3 系统稳定性分析
将系统方程写为如下形式:
式中:δ(t,x,u)为由死区非线性环节和饱和非线性环节共同组成的综合非线性环节。
由于系统中存在的饱和、死区非线性环节以及设计的滑模控制器中存在的符号函数,常规的分析方法并不能较好地分析此类系统的稳定性,因而结合如下定理对整体系统的稳定性进行分析。定理[15]考虑系统为
定义的正不变集Ωε,此外,如果假设全局成立,V(η)径向无界,则上述结论对于任意初始状态都成立。参照上述定理,对于式(13)定义的系统,有:
由上所述,δ对t分段连续,且对于(x,u)充分光滑。由于饱和非线性环节的存在,δ(t,x,u)必有界,则满足式(15)定义的条件;取Lyapunov 函数
又由于只需存在Φ(η),使得:
所以必能找到符合条件的Φ(η),使式(18)定义的条件成立。综上所述,可以判断整体系统可以稳定到达滑模面。
4 仿真验证与比较
针对上文设计的基于趋近律的滑模控制律进行仿真验证。利用Matlab 中的Simulink 搭建模块进行仿真,选择仿真步长为0.001 s,按照第2 部分给出的参数整定原则进行参数整定,最终确定的参数为:ε=685,k=80,c=80。当输入信号为1 rad阶跃信号时,使用滑模控制器得到效果如图4所示。

图4 滑模控制器控制回路角位置输出结果Fig.4 Output results of the control loop angular position of the sliding mode controller
通过图4 可以看出,当控制回路使用滑模控制器时,上升时间(2%)为0.065 1 s,角位置在0.15 s 时达到预定值,系统无超调。针对滑模控制器常见的稳态抖振问题,选择0.270~0.273 s 进行局部放大观察。可以发现,此时系统的稳态抖振远远小于预定值,可以认为此抖振不影响系统整体性能。为了研究比较滑模控制器对于饱和、死区等非线性环节的抑制效果,分别使用不包含饱和、死区等非线性部分的线性模型与非线性模型进行仿真,比较结果如图5所示。
通过图5 的结果可以看出,由于线性模型中不包含饱和、死区非线性环节,所以当系统模型是线性模型时,控制效果更好。对于非线性模型而言,虽然控制效果相较于线性模型略有降低,但降低的程度不大,可以认为滑模控制器对于抑制饱和、死区等非线性环节具有一定的效果。
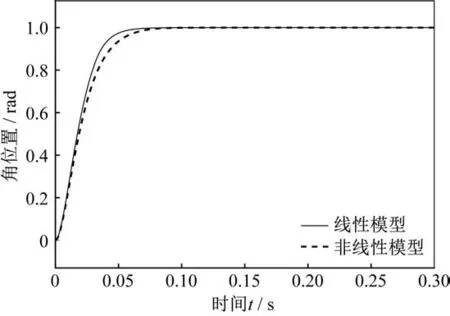
图5 非线性模型与线性模型滑模控制效果比较Fig.5 Comparison of the control effects of the nonlinear and linear sliding modes
为了比较验证滑模控制器对于系统中非线性环节的抑制效果,针对前文中得到的模型按照传统线性超前滞后方法设计相应的控制器,作用于同样的系统,比较滑模控制器与线性超前滞后控制器的性能区别。按照传统的超前滞后方法设计出的控制器传递函数为[16]
首先选择不存在饱和、死区等非线性环节的模型进行仿真,比较滑模控制器与传统线性控制器性能,如图6 所示。
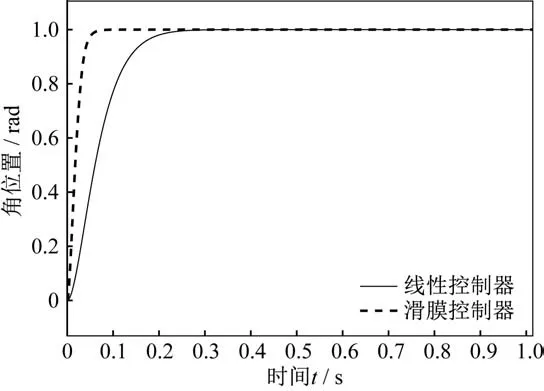
图6 线性模型滑模控制器与线性控制器性能比较Fig.6 Performance comparison between the linear sliding mode controller and the linear controller
通过图6 的结果可以看出,在被控对象不存在饱和、死区等非线性环节时,无论是线性控制器还是滑模控制器都能完成控制回路的预定功能。不同的是,滑模控制器有着更好的动态性能,能够更快地、无超调地达到预定值,线性控制器如果要继续减小调整时间,势必要增大控制器增益,而控制器增益的增大又会导致系统出现超调。因此,从快速性与超调的角度来看,滑模控制器的性能优于线性超前滞后控制器。
比较验证当系统模型中存在饱和、死区非线性时,线性超前滞后控制器与滑模控制器的控制性能。在不改变参数的情况下,线性控制器与滑模控制器得到的控制曲线如图7 所示。
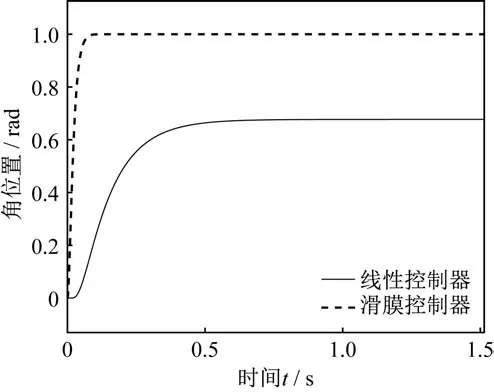
图7 非线性模型滑模控制器与线性控制器性能比较Fig.7 Performance comparison between the nonlinear sliding mode controller and the linear controller
可以看出,当模型中出现非线性环节时,滑模控制器仍能无差地快速达到预定值,但对于线性控制器而言,如果不调整增益,会出现较大的稳态误差,并且初始上升速度过慢。要消除这些问题,需要调整控制器增益,通过多次调整,要想保证线性控制器控制回路无稳态误差,需要将控制器增益提高到52.5。从参数整定的角度来看,当被控对象中含有非线性环节时,线性控制器需要重新大幅度调整控制器增益,而滑模控制器不调整参数也可以获得较为理想的控制效果,所以可以认为滑模控制器比线性超前滞后控制器有更好的抑制非线性的能力。
综合前面的结果可以得出如下结论,首先,滑模控制器可以完成控制回路的控制任务,能够快速、无差、无超调地实现导引头伺服系统角度预定功能。其次,当被控对象模型为不含饱和、死区等非线性环节的线性模型时,传统的线性超前滞后控制器与滑模控制器都能够较好地完成控制回路的功能,但是从过渡过程的角度来看,滑模控制器的过渡过程优于线性超前滞后控制器的过渡过程。另外,通过仿真分析可以发现,滑模控制器对于系统中的非线性环节并不十分敏感,有无非线性环节对于滑模控制器的控制效果影响有限,而传统的线性超前滞后控制器对于系统中的非线性环节还是较为敏感的,系统中的非线性环节会明显影响到整个回路的控制效果,虽然非线性环节造成的影响可以通过调整控制器增益来进行弥补抵消,但是这种方式无疑会增加现场调试过程的任务量,而对于滑模控制器而言,即使系统中存在一定未建模非线性环节,对于整体控制回路的控制性能影响也相对有限,所以对于大多数情况即使不重新调整控制参数也可以获得较为理想的控制效果。
5 结束语
本文针对导引头伺服控制系统预定回路设计了一个基于趋近律的滑模控制器,并结合具体的经过工程实践检验的模型进行了相关的仿真验证。通过仿真验证证明,滑模控制器能够获得较好的预定回路控制效果,且对于非线性环节具有较好的抑制能力,为进一步的工程实践奠定了理论基础。
