幂律稠油砂岩油田单井探测半径计算

谢明英，刘国涛，闫正和，施征南，孙晓娜

中海石油（中国）有限公司深圳分公司，广东 深圳518000

引言

海上油田开发成本高，要达到少井高效开发，在进行开发方案设计的时候，对油井探测半径有较好的认识是非常必要的，特别是稠油边际油田，这种需求就更加迫切。南海东部地区某海上油田稠油的流变性表现出幂律稠油的特征，为了更好地指导该油田井网部署、开发方案编制、储量评估等，本文针对此类油藏的油井探测半径开展了研究。

探测半径是油田开发过程中的一个重要参数，它指油井开井生产一段时间后压力传播的径向距离，这是一个相对定性的概念[1-5]。正因为如此，关于探测半径的计算公式，目前，相关行业没有统一的规范和标准，许多学者围绕这个概念进行了定量化的研究[6-12]。2010 年，李传亮等采用压力脉动波传播理论，推导了平面单向流的探测距离计算公式[13]。2014 年，王刚等提出近似绘制理论压降漏斗剖面来计算探测半径[14]。2015 年，陈志明等针对低渗透致密气藏，研究了考虑渗透率和黏度变化情况下水平井的探测半径[15]。2017 年，张快乐等针对低渗透致密油藏，推导了考虑渗透率和黏度变化情况下直井探测半径方程[16]。2019 年，针对储层物性发生变化的复合油藏，邓琪等推导了双重及多重径向复合油藏的探测半径及地层压力分布解析公式，分析了复合分区流度的比值对复合油藏探测半径的影响[17]。陈志明等曾总结了国内外油井探测半径的计算公式[18]。此外，2020 年，Bresciani 等[19]对探测半径的定义及评价方法进行了较为全面的论述。

针对牛顿流体的探测半径研究已有大量的文献报道，Van Poolen 最早提出探测半径的概念，并推导出探测半径计算公式，其系数为2，与后来的学者得到的探测半径的计算公式可统一为一种形式。关于非牛顿流体探测半径的研究报道相对要少一些[20-23]。1995 年，王新海等根据稳态依次替换法推导了无限大地层幂律型非牛顿流体单相流动时的探测半径[24]。2007 年，齐丽魏等通过幂律型非牛顿流体拟稳态渗流井壁压力晚期渐近公式，推导了探测半径计算公式[25]。

目前的文献中，无论是牛顿流体还是幂律流体，鲜少考虑井筒储集效应和表皮效应。南海东部海域稠油砂岩油藏，埋深浅、储层疏松，在实际生产中，储层微粒运移是无可避免的，某些井生产动态表现出近井地带储层受到污染，生产效果不及预期好。同时，本地区幂律稠油油田发现日趋增多，深入理解这类油田单井探测半径，对指导井控储量评价、井网部署等有非常重要的作用。

本文研究考虑了井筒储集效应和表皮效应，借助探测半径的相对判断准则，利用Laplace 变换和Stehfest 数值反演的方法，研究了无限大地层幂律稠油（流性指数0.80∼1.00）探测半径与时间、压力的关系，为幂律稠油试井设计、产能评价、井控及井网设计等提供理论指导，以使这类油田能更好地实现高速高效开发。此外，研究成果不仅可以用来指导试井设计和试井解释，还能有助于油田在注入幂律流体以提高采收率技术的推广应用，比如聚合物驱、多元驱、表面活性剂驱等。

1 传统探测半径计算公式

均质油藏牛顿流体直井探测半径公式的形式可统一为[18]

常用的传统探测半径计算公式没有考虑井筒储集效应和表皮效应。海上油田DST 测试成本高，非常希望能在更短时间内达到测试目的。为了更好地实现幂律稠油测试目的，非常有必要在试井设计时充分考虑各种不确定性因素的影响，本文考虑了井筒储集效应和表皮效应的影响。文中采用的方法还能用于牛顿流体的情况，当流性指数取1.00 时，地层流体为牛顿流体，研究考虑井筒储集效应和表皮效应情况下牛顿流体的探测半径，弥补了传统探测半径计算公式的不足。

2 数学模型建立

2.1 幂律稠油渗流数学模型

研究中，采用各向同性、均质等厚圆形油藏，岩石和流体微可压缩且压缩系数为常数，地层流体为单相、流性指数n∈(0,1.00]，考虑井筒储集效应和表皮效应，忽略重力的影响，中心有一口直井，以直井为中心，建立平面极坐标系，则幂律稠油平面径向渗流方程的无因次形式为[26]

式中：

pD，rD—无因次压力和无因次径向距离；

n—流性指数，无因次；

tD— 无因次时间。

对无限大地层情况，初始和边界条件为

变换前的空间称为原空间，变换后的空间称为Laplace 空间。则式（3）、式（4）通过Laplace 变换后，可得到

于是，幂律稠油在水平均质无限大圆形地层中渗流，其Laplace 空间无因次压力和无因次井底压力分别为

式中：

pwD—Laplace 空间下的无因次井底压降；

Kv(z)—v 阶第二类修正贝塞尔函数；

v —贝塞尔函数的阶数，v=(1 −n)/(3 −n)。

在考虑了井筒储集效应和表皮效应的模型中，式（8）和式（9）难以得到原空间的解析解，这里采用Stehfest 数值反演方法来得到原空间的数值解。Stehfest 反演公式为[13]

式中：N—偶数，在多数情况下，取N=8，10 或12，本文取N=10；

Vi—Stehfest 反演常数组；

k,i—计数变量。

2.2 探测半径判断准则

探测半径是一个相对定性的概念，为了量化它，提出了多种定义，可按某处压降大小来定义，也可按某处压降占井底压降的比值来定义。

文献[10]指出，用来定量研究探测半径的判断准则分为两大类，第一类判断准则是绝对准则，即在探测半径处压力扰动值等于某个小值，这个小值可由压力分辨率来确定[2]；该准则能直观地了解压力扰动能达到的距离，远于这个距离压力扰动太小而压力计不能有效监测到。第二类判断准则是相对准则，即探测半径处的压降与油井井底压降的比值等于某一阈值（常用0.01），探测半径范围内，各处压降对油井的影响不能忽略[10]；利用这个准则，可以为油田开发方案设计时最小井间距的选取提供信息，以避免严重的井间干扰。

为了更好地指导幂律稠油油田井网部署、开发方案编制，这里采用第二类准则来研究海上幂律稠油砂岩油田的单井探测半径，阈值取0.01，即

结合式（8）∼式（11），可计算得到考虑井筒储集效应和表皮效应幂律稠油探测半径，这为幂律稠油探测半径的研究提供一种新的计算方法。

与传统的牛顿流体探测半径计算公式相比，文中提出的幂律稠油探测半径计算方法考虑因素多，不仅考虑了传统计算中的储层和流体因素，还考虑了流性指数、井筒储集效应和表皮效应的影响，同时还能用于牛顿流体探测半径的研究。

3 探测半径研究

3.1 参数设计

根据南海东部地区幂律稠油的特征，基于幂律稠油渗流数学模型和探测半径判断准则，针对不同的研究内容和目的，对流性指数n、井筒储集效应CD和表皮系数S取值进行了设计，分别研究了它们对探测半径的影响。

3.2 模型验证

关于传统的探测半径计算公式，Van Poollen根据泄油面积得到探测半径计算系数为2.000，Gringarten 等利用压力导数曲线得到两个探测半径计算系数，李传亮等根据理论压降漏斗的外部边缘定义了探测半径，得到探测半径计算系数为1.500，毛伟利用无限大地层的流量分布公式为基础，得到探测半径计算系数为2.195。针对牛顿流体考虑不同因素，得到的计算系数略有差别。但从矿场实际应用情况来看，2.000 是矿场公认的最常用的探测半径计算系数。

利用式（8）∼式（11）来计算n=1.00（牛顿流体）、CD=0 和S=0 时的无因次探测半径，与Van Poollen的结果进行对比见图1。

由图1 可见，计算结果与Van Poollen 非常接近，与矿场公认的最常用的探测半径计算结果一致，当无因次时间为109时，与Van Poollen 的结果相比，本方法得到的探测半径相对误差仅为0.57%，当矿场计算得到的探测半径为500.00 m 时，用本方法得到的探测半径为502.85 m，说明本文的计算模型可靠，可以用于矿场应用。

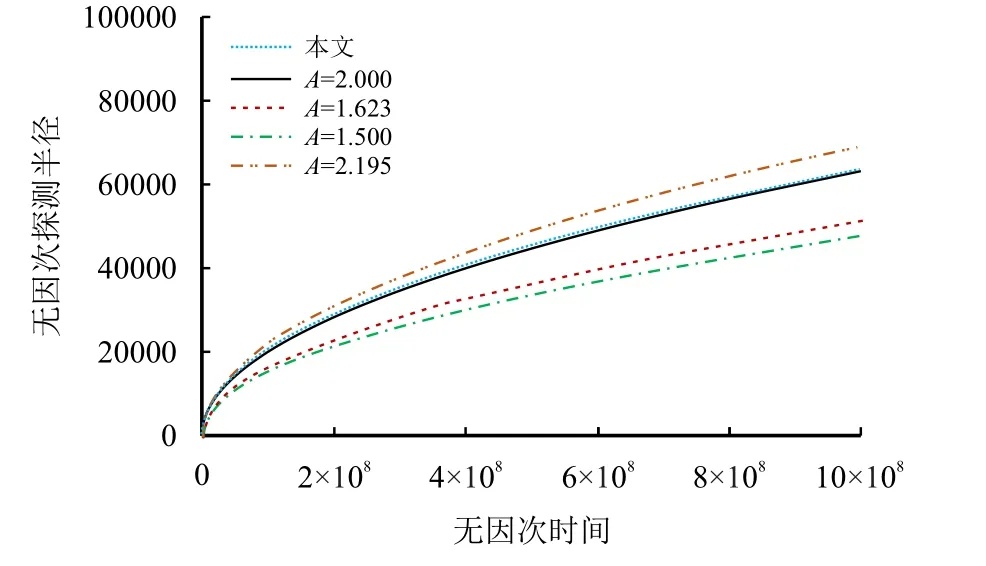
图1 无因次探测半径随无因次时间的变化曲线（n=1.00）Fig.1 The curve of dimensionless investigation radius with tD（n=1.00）

3.3 流性指数的影响

为了更好地显示这3 个参数对探测半径的影响，利用无因次探测半径与n=1.00，CD=0，S=0 时无因次探测半径的比值来显示探测半径随时间的变化幅度。为了方便，用rinvD1,0,0来表示牛顿流体不考虑井筒储集效应和表皮效应时的无因次探测半径。

基于南海东部海域稠油流性指数的分布，取n为0.80、0.90 和1.00，分别计算了不考虑井筒储集效应和表皮效应（CD=0、S=0）的无因次探测半径，并与牛顿流体、不考虑井筒储集效应和表皮效应时的无因次探测半径进行了对比，来分析流性指数对无因次探测半径比值的影响，见图2。

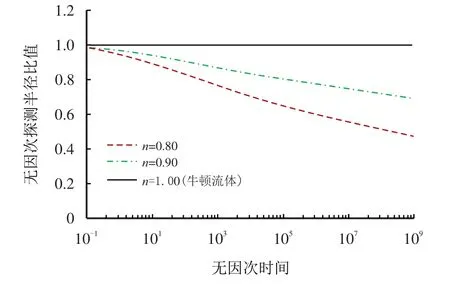
图2 流性指数对无因次探测半径比值的影响曲线Fig.2 The influence curve of power law index on dimensionless investigation radius ratio

如图2 所示，CD=0 和S=0 时，流性指数n越小，无因次探测半径比值（rinvD/rinvD1,0,0）越小，稠油幂律特征越明显，相同无因次时间对应的探测半径越小；时间越长，无因次半径减少越多，比值曲线呈下降趋势。n=0.80 和0.90 时，在研究时间范围内，比值分别下降到50%和70%左右，即与牛顿流体相比无因次探测半径分别减少了1/2 和1/3。对这类稠油进行DST 测试时，若是进行探边测试，则需要延长测试时间；当无因次探测半径约为1 000 时，n分别为0.80 和0.90 所需延长的无因次时间是n=1.00时的1.5 倍和0.6 倍，物性参数不同，探边的距离不同，延长的时间也不同。

3.4 井筒储集效应的影响

当n=0.90、S=0 时，计算了CD取不同值时的无因次探测半径，并与牛顿流体、不考虑井筒储集效应和表皮效应时的无因次探测半径rinvD1,0,0进行比较，比值变化曲线见图3a。从图3a 可见，流性指数对无因次探测半径的影响占主导，比值曲线整体呈下降趋势；井筒储集效应CD影响了早期阶段的无因次探测半径，CD越大，无因次探测半径越小，井筒储集效应影响的无因次时间越长；随着无因次时间的增加，井筒储集效应的影响逐渐减弱至消失。这是因为井筒储集效应使开井早期阶段的井底压力偏离理论值，在某一时刻该效应消失，之后无因次探测半径受流性指数影响。

图3b 为牛顿流体（n=1.00）井筒储集效应对探测半径的影响曲线，与幂律流体相比，不同之处在于，随着无因次时间的增加，井筒储集效应消失时无因次探测半径比值为1。对牛顿流体和幂律流体，井筒储集效应使无因次探测半径减少，储集效应越强，影响时间越长、无因次探测半径越小；相同条件下，牛顿流体无因次探测半径最大，稠油幂律特征影响整个时间阶段，让无因次探测半径更小。当n=0.90、S=0 时，CD为1、10、100 和1 000 时，井筒储集效应作用的无因次时间分别为100、1 995、31 623和398 107。为了让测试相同时间内探测的半径更远，也为了缩短测试时间降低成本，达到DST 测试目的，降低井筒储集效应的影响是非常必要的。

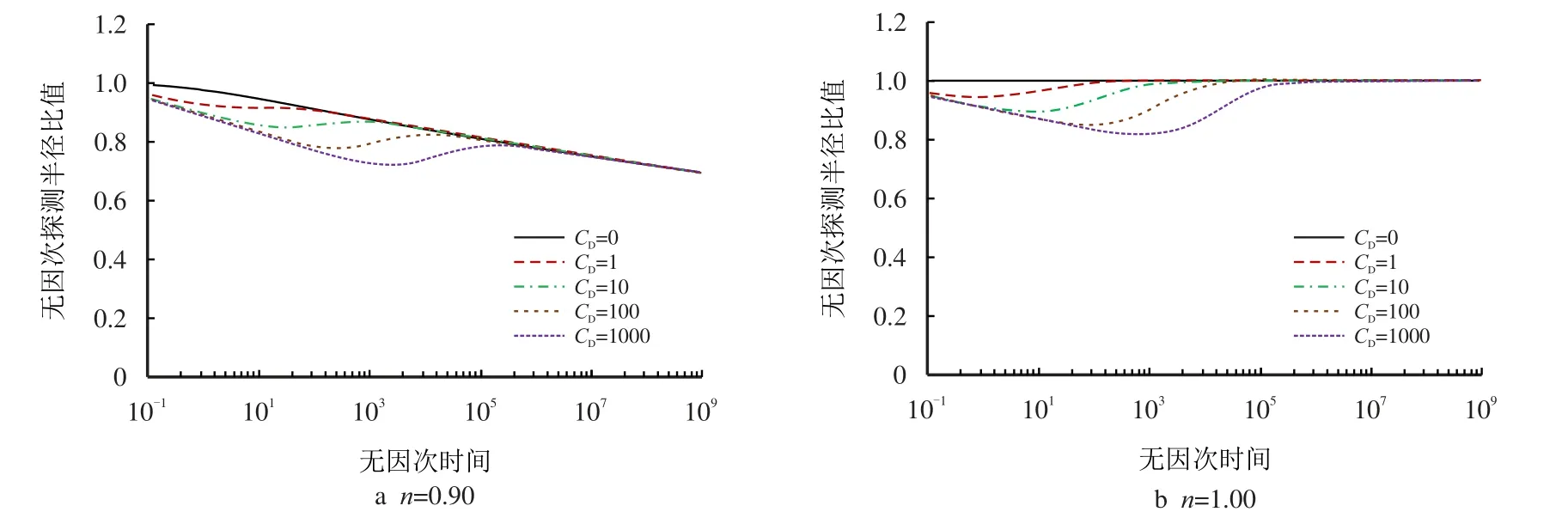
图3 井筒储集效应对无因次探测半径比值的影响曲线（S=0）Fig.3 The influence curve of wellbore storage effect on dimensionless investigation radius ratio（S=0）

3.5 表皮效应的影响

针对南海东部海上稠油油藏开发特点，假定储层疏松引起微粒运移产生的近井地带储层污染表皮系数S在1∼10，利用本研究方法计算得到的无因次探测半径，并与牛顿流体、CD=0、S=0 时的无因次探测半径rinvD1,0,0进行比较。取n=0.90、CD=0 时，比值变化曲线整体呈下降趋势，S越大比值越小，且逐渐趋近于S=0 的比值曲线，如图4a 所示。在研究时间内，早期阶段，表皮效应对无因次探测半径的影响较大，随着无因次时间的增大，流性指数n的影响占主导，在与表皮系数S的共同作用下，无因次探测半径比值降低到0.6∼0.7。n=1.00，CD=0 时，比值曲线随无因次时间增大呈现出先减小再增大然后趋近水平的趋势，见图4b。这是因为在早期井底压降主要用于克服表皮效应引起的压降，比值曲线减少，随着无因次时间的增大，井底压降逐渐增大，比值曲线呈上升趋势并逐渐趋近于S=0 的那条线，S越大无因次探测半径比值越小。与井筒储集效应CD的影响不同，表皮效应对无因次探测半径的影响一直都存在，比值曲线始终小于1；在稠油幂律特征与表皮效应共同作用下，使无因次探测半径更小。当n=0.90、CD=0 时，以tD=100 000 为例，S取值为0、1、2、5 和10 时，无因次探测半径分别为738、711、687、629 和558，探测半径减少了约4%∼25%。对疏松砂岩幂律稠油油藏，在井网设计时可适当考虑表皮效应带来的影响，适当缩小井距。

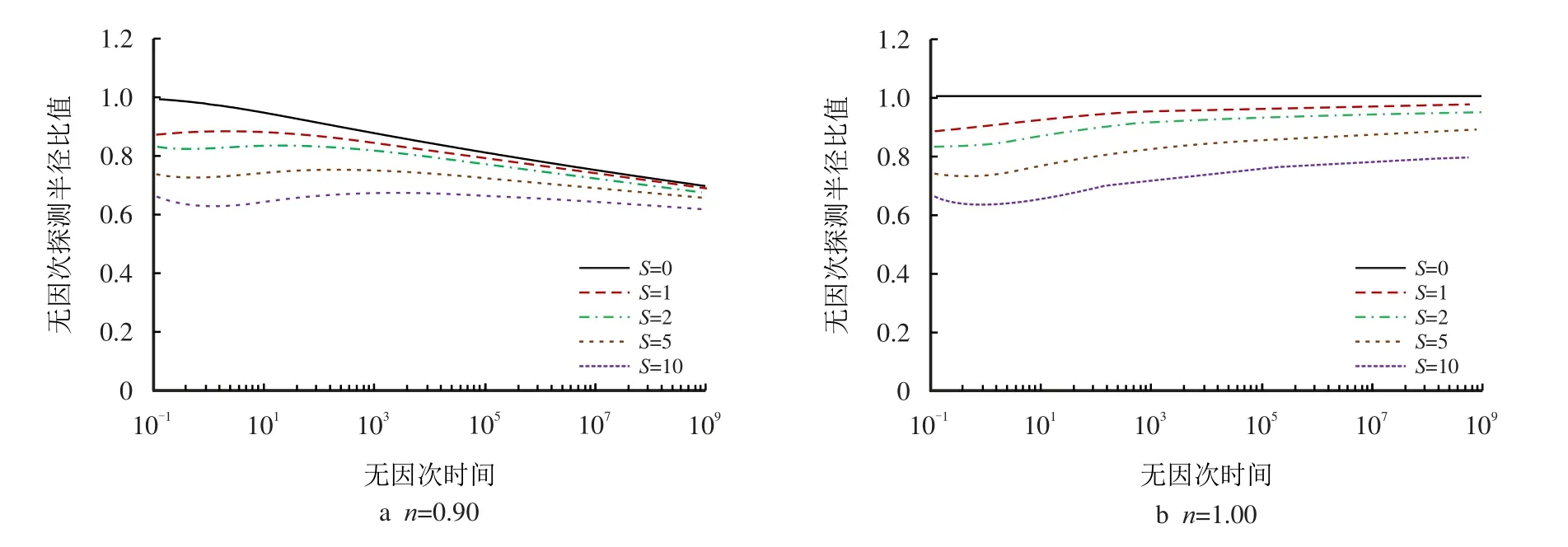
图4 表皮效应对无因次探测半径比值的影响曲线（CD=0）Fig.4 The influence curve of skin effect on dimensionless investigation radius ratio（CD=0）

3.6 幂律稠油探测半径随时间的变化关系

不考虑井筒储集效应和表皮效应，分析不同流性指数的无因次探测半径与无因次时间的关系，见图5。由图5 可见，当CD=0、S=0 时，无因次探测半径与无因次时间呈很好的指数关系，n=0.80 时，，决定系数0.998 9；n=0.90 时，，决定系数0.998 8；n=1.00 时，，决定系数0.998 8。

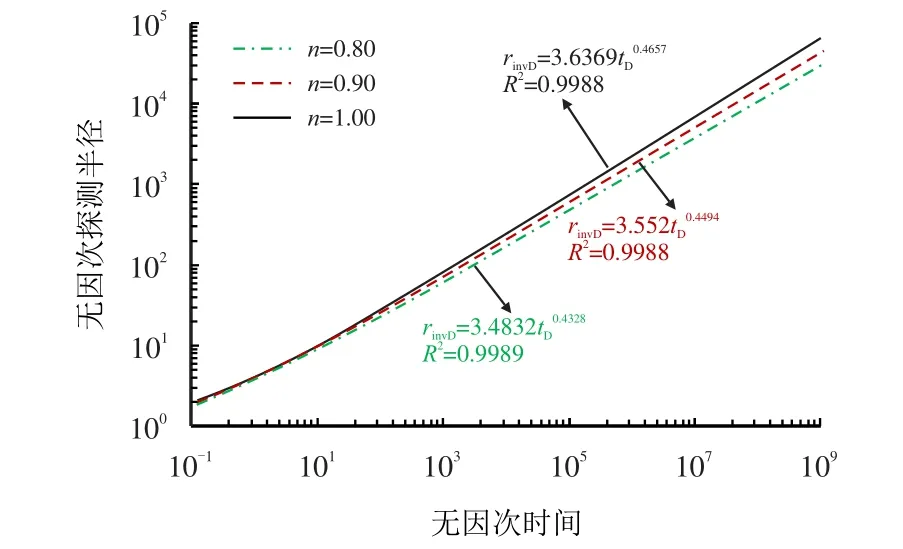
图5 不同流性指数时无因次探测半径随无因次时间的变化曲线（CD=0，S=0）Fig.5 The curve of dimensionless investigation radius with tD for different power law index（CD=0,S=0）

CD=0、S=0 时可用的形式来描述无因次探测半径与无因次时间的关系，基于数值计算，不同n时的B1和B2值见表1。

表1 不同n 时的B1 和B2 值（CD=0，S=0）Tab.1 The value of B1 and B2 with different n（CD=0,S=0）

B1和B2值与流性指数n呈线性相关，见图6，B1与n的线性关系为：B1=0.7656n+2.8670，B2与n的线性关系为：B2=0.1646n+0.3012，决定系数0.996 1 以上。

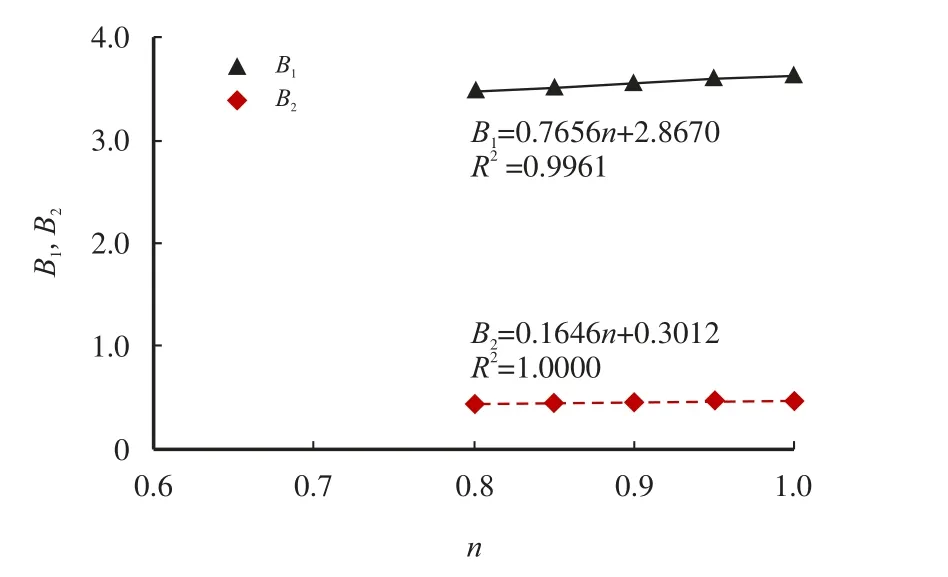
图6 B1 和B2 值与流性指数的关系（CD=0，S=0）Fig.6 The relationship between the value of B1 and B2 and power law index（CD=0,S=0）

根据南海东部海域稠油流性指数分布，不考虑井筒储集效应和表皮效应，利用B1和B2值与n的线性关系，得到n在0.80∼1.00 时无因次探测半径计算公式，为此类幂律稠油油田DST 测试设计、井网设计等提供一种快速评价方法。对疏松砂岩油藏，可以用相同的方法来分析表皮效应不同时无因次探测半径与时间的关系，这里不再一一赘述。

3.7 幂律稠油探测半径与生产压差的关系

在进行井网设计、井控储量评价中，会出现给定生产压差来研究井控范围的情形。基于数值计算，这里给出了CD=0 时不同S无因次探测半径与无因次井底压降的关系，见图7。无因次探测半径与无因次井底压降正相关，无因次井底压降越大，无因次探测半径越大；同一无因次探测半径，S越大井底压降越大。同时，流性指数n影响了无因次探测半径，即便在CD=0、S=0 时，无因次探测半径与无因次井底压降拟合公式的相关性比牛顿流体的略差，牛顿流体拟合公式的决定系数在0.999 5 以上；在满足油藏工程精度的情况下，也可用图7a 中拟合的公式来粗略估算n=0.90 时某一无因次井底压降能对应的无因次探测半径；在不满足精度的情况下，采用数值方法进行研究。

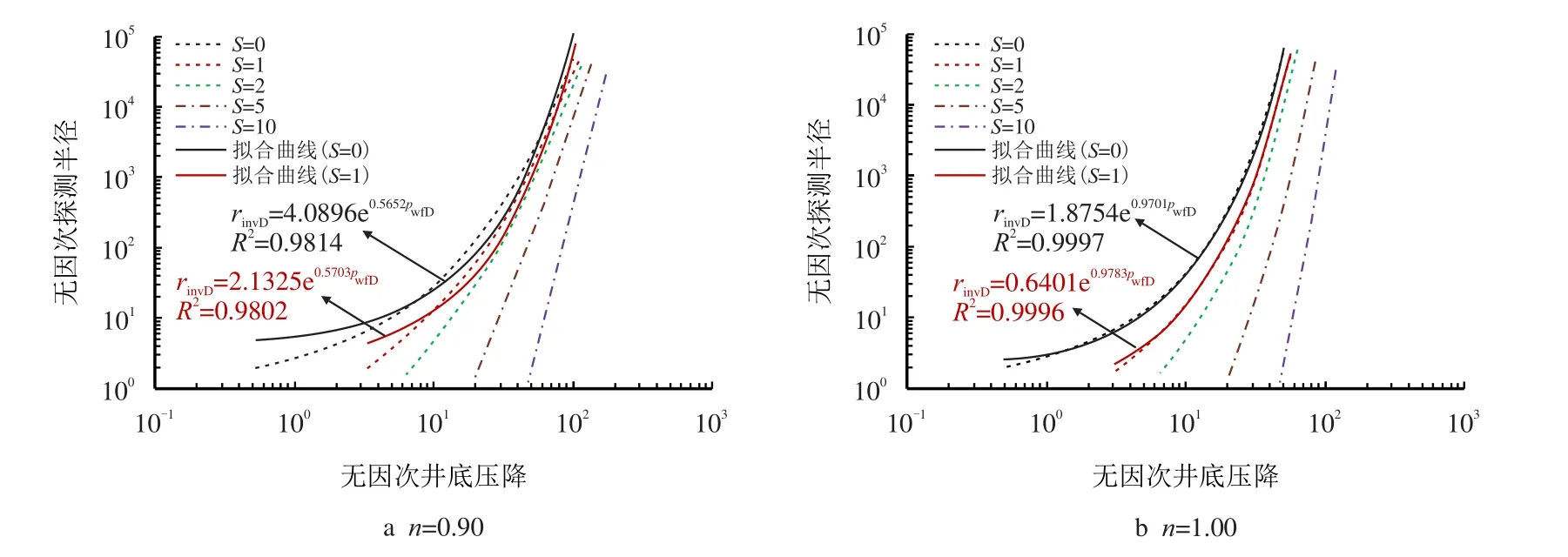
图7 不同S 时无因次探测半径随无因次井底压降变化曲线（CD=0）Fig.7 The curve of dimensionless investigation radius with pw f D for different S（CD=0）

4 实例应用

南海东部地区某幂律稠油油田以边水油藏为主，原油流变性实验显示，流性指数n=0.90，油藏原始地层压力为13.33 MPa，有效厚度为2∼4 m，渗透率166∼320 mD，地层原油黏度为278.00 mPa·s，地层水黏度为0.49 mPa·s。在油田开发过程中，由于油藏高部位油井受两条相交断层影响出现天然水体能量供给不足的问题，为了弥补天然水体能量供给不足，油田开展了井网调整和人工注水方案的研究。

由于水体能量供给不足，油井一直以低油量和低液量生产，含水率低于5%。同时为了简便，在注采井网研究中，油井生产近似为单相流。针对注采井分别建立压力分布计算模型来研究极限注采井距。以油井为中心建立坐标系，得到油井周围压力分布，通过探测半径判断准则，即探测半径处的压降与油井井底压降的比值等于0.01 时，计算得到的探测半径就是油井的极限生产半径；在注采井网中，地层压力是连续的，为了保证压力场的连续性，对注入井，与油井不同之处在于，探测半径判断准则中注水井探测半径处的压降与油井探测半径处的压力有关，且注水井注入流体为牛顿流体，流性指数取1.00，其他与油井相同，得到注入井的极限注入半径，则极限注采井距等于极限生产半径与极限注入半径之和。

假设油井以历史最高生产压差3.3 MPa 生产，注水井按极限注入压差5.0 MPa 注入。采用本文方法计算得到油井无因次井底压力和探测半径，然后结合上述油藏和油井基本数据，计算得到生产压差为3.3 MPa 时油井极限生产半径为220 m；注水井注入压差为5.0 MPa 时，注水井的极限注入半径为350 m；极限注采井距为570 m。以油井为中心建立坐标系，注采井间地层压力分布见图8。根据该计算结果，结合已有生产井网和构造特征，注水井井位优选为距离油井500 m 处。

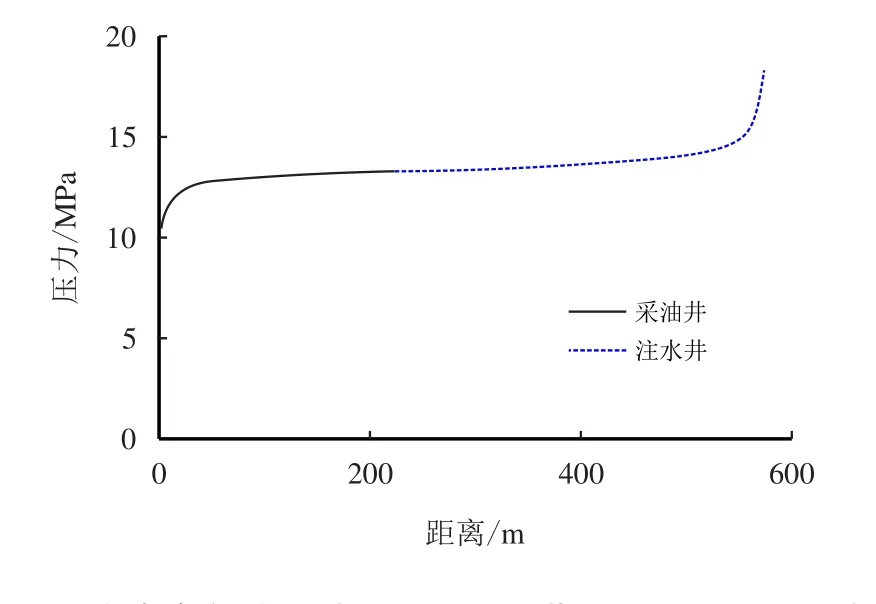
图8 南海东部地区某幂律稠油油藏注采井间压力分布Fig.8 The pressure distributions of injection-production well in power law heavy oil reservoir of eastern South China Sea

表2 给出了油井注水前后的生产指标，结果表明，油井注水后平均产油量从35.20 m3/d 提升到82.34 m3/d，提升了47.14 m3/d，提升幅度为133%；同时，含水率从4.8%下降到4.3%，下降了0.5 个百分点，下降幅度为10%。从油井注水前后生产指标对比来看，注水后油井日产液提高，能量得到了有效补充，日产油实现了翻一番，油井受效显著。结果证实，用文中提出的幂律稠油探测半径计算方法得到计算结果可靠，可用于现场实践。

5 结论

1）传统探测半径计算公式没有考虑井筒储集效应和表皮效应的影响，且不适用于幂律型非牛顿流体。提出的新探测半径计算方法既能用于幂律稠油探测半径的计算，还能用于常见的牛顿流体探测半径的计算。

2）流性指数、井筒储集效应和表皮效应对探测半径的影响均有较大影响：流性指数为0.80 和0.90的幂律流体的无因次探测半径比牛顿流体的无因次探测半径分别减少了1/2 和1/3。对这类稠油进行DST 测试时，若是进行探边测试，则需要延长测试时间；井筒储集效应作用的无因次时间随井筒储集系数的增大而增大。为了让测试相同时间内探测的半径更远，也为了缩短测试时间降低成本，以便达到DST 测试目的，降低井筒储集效应的影响是非常必要的；早期阶段，表皮效应对无因次探测半径的影响较大，随着时间的增加，流性指数的影响占主导，都会减小探测半径，在进行井网设计时，根据实际情况适当缩小井距。

3）基于新方法拟合得到了适用于幂律稠油的探测半径计算公式，研究了探测半径与井底压降的定量化关系。

4）新方法指导了南海东部地区某幂律稠油油藏的井网部署和注采井网设计，注水后油井日产油明显增加，含水率下降，油井受效显著，获得了很好的应用效果。现场应用证实，新方法得到计算结果可靠，可用于现场实践。该方法不仅为幂律稠油探测半径的研究提供了一种新思路和理论计算依据，还为注入幂律流体提高油田采收率研究和应用提供理论指导。