基于边界元理论的气藏不稳定渗流模型研究
2023-05-10陆正元
邓 波 ,陆正元,赵 娜
1.油气藏地质及开发工程国家重点实验室·成都理工大学,四川 成都610059 2.中国石油西南油气田分公司川西北气矿,四川 江油621700 3.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都610500
引言
四川盆地作为中国主要油气富集盆地之一,各类气藏广泛分布,其中,碳酸盐岩气藏总资源量高达39.9×1012m3。以龙王庙为代表的碳酸盐岩气藏是迄今为止中国发现的单体最大的碳酸盐岩整装气藏,有力保证了西南油气田分公司300×108m3产能的快速上产[1-3]。
近年来,西南油气田分公司在川西北双鱼石区块的超深层碳酸盐岩气藏持续取得突破,气藏埋深超过7 000 m,压力系数1.33,温度约158◦C,天然气硫化氢含量5∼12 g/m3,为典型的超深高温高压含硫气藏,该气藏目前正处于试采评价阶段,不同于龙王庙气藏,川西北双鱼石区块栖霞组气藏的构造复杂程度(山前褶皱带,断块发育)、苛刻的地质条件远大于龙王庙气藏,给气藏早期开发评价认识及生产动态预测带来了巨大挑战[4-5]。研究认为,不同于塔里木深层碳酸盐岩气藏以大型溶洞和裂缝系统为主要储集空间类型的特点,川西北双鱼石区块栖霞组碳酸盐岩气藏储层受沉积、成岩以及复杂构造等多因素的影响,储层主要储集空间是孔隙(图1a)和溶蚀小孔洞(图1b)、天然裂缝局部发育(图1c),主要起到改善储层渗透性的作用,生产动态表现出不规则边界响应下的双重介质的特征。

图1 川西北双鱼石区块栖霞组碳酸盐岩气藏储集空间及断层分布特征Fig.1 Pore space and fault distributions of carbonate gas reservoir in Qixia Formation,Shuangyushi Area,northwest Sichuan Basin
由于常规试井解释理论与方法只能处理无限大或规则外边界条件下的气井不稳定渗流问题,导致其在川西北双鱼石区块栖霞组气藏气井试井应用过程中适应性差的缺点。因此,如何开展复杂外边界条件下的气井试井模型研究对于后期气藏跟踪测试与评价具有重要的理论和现实意义。
气井试井分析作为气藏开发过程中重要的动态监测手段与方法,对于准确评价气藏储层物性参数、探测边界等具有重要作用。试井分析技术的关键是如何建立准确的物理模型来表征气井生产过程中的储层和边界条件,以及对模型进行准确求解。调研发现,对于双重介质储层的表征手段主要有Warren–Root 模型、De–Swaan 模型和Kazemi 模型,如图2 所示。对于规则边界条件下的气井不稳定渗流模型的求解方法主要有解析法、半解析法和数值解法等。前两种求解算法能够很好处理规则外边界条件下的渗流模型,前人分别利用积分变量法、Laplace 变换、源函数等方法对常规和非常规油气藏直井、压裂井和分支井等各种复杂结构井在无限大、圆形、条带形和矩形等各种规则外边界条件下的不稳定渗流模型进行了系统研究,取得了丰硕成果。而数值解是伴随计算机技术发展逐渐兴起的一种新型计算方法,因其能够处理各种强非均质性难题而得到广泛应用,数值试井技术就是其应用分支之一。
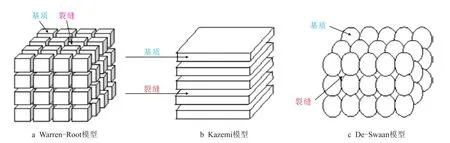
图2 双重介质储层连续介质等效模型示意图Fig.2 Schematic of continuum equivalent models for dual porosity reservoir
目前,数值试井的主要求解方法有有限差分法、有限元法、有限体积法及边界元法等[6-10]。边界元法作为一种边界型数值方法,是继有限差分和有限元法之后发展起来的一种新型数值计算方法[11-17]。与有限元和有限差分法在连续体域内划分单元的思想不同,边界元法只在定义域的内外边界上进行离散,用满足控制方程的基本解去逼近边界条件(图3)。相比有限元法和有限差分法,边界元法具有单元个数少、数据准备简单,而且基本解具有解析解的基本性质,使得边界元法在研究复杂边界和复杂结构井不稳定渗流理论上具有一定优势。
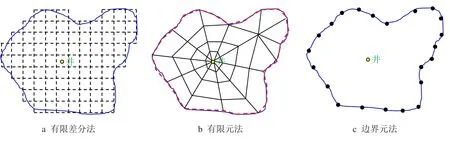
图3 各种数值求解方法网格离散示意图Fig.3 Schematic of discrete grid for different numerical solutions
国内外边界元法在试井领域的应用研究表明,该方法主要用来研究不规则外边界储层和局部存在非均质或非渗透区域的油气井不稳定渗流。本文以川西北双鱼石区块栖霞组气藏储层为研究背景,开展了基于边界元理论的双重介质复合气藏任意边界条件下的不稳定渗流理论研究,探究不同边界条件、不同储层物性参数下的气井试井曲线特征,明确栖霞组碳酸盐岩复杂构造气藏不同边界条件下的动态特征,为气井后期生产动态测试与评价提供理论支撑。
1 复合气藏直井数学模型
1.1 复合气藏直井数学模型的建立
基于川西北双鱼石区块栖霞组气藏地质条件,选用双重介质模型予以考虑。图4 为一任意外边界双重介质复合气藏中心一口直井以定产量生产的物理模型示意图,模型分内区和外区。
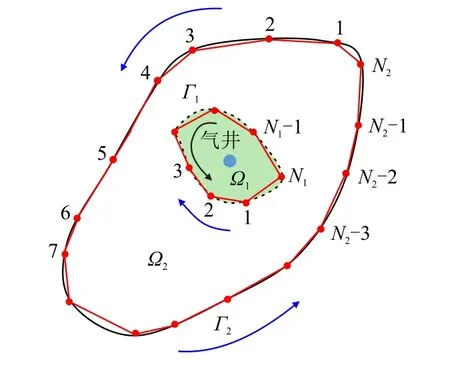
图4 任意边界形状复合双重介质气藏物理模型示意图Fig.4 Physical model of composite dual porosity reservoir with arbitrary outer boundary
根据物理模型描述,对模型建立Laplace 空间下考虑内边界的复合气藏无因次渗流微分方程,内区和外区的微分方程有所不同。对于内区,无因次渗流微分方程为[16,18]
对于外区,无因次渗流微分方程为
对于非稳态窜流
式(7)和式(8)中,内区时,i=1,g(s)=s;外区时,i=2,g(s)=sη12。
1.2 基于边界元法的复合气藏模型求解
为较好地处理气藏复杂边界问题,边界元求解不稳定渗流模型的基本思路为将目标区域内的微分方程变成边界上的积分方程,然后将边界分割为有限大小的边界单元,利用端点线性插值函数近似,即将边界积分方程离散为代数方程,进而将微分方程的求解转换为代数方程的求解问题。
基于内外边界处的数值,利用叠加原理求取地层中任意点处的无因次拟压力。考虑表皮和井筒储集系数,无因次井底拟压力为[16,19]
2 气井不稳定压力动态响应特征及影响因素分析
2.1 模型实例验证
为了验证本文建立的模型和方法的正确性,将复杂外边界简化为圆形内外边界,此时物理模型就转换为圆形复合气藏,该模型可以采用源函数法和数值方法进行求解(图5)。
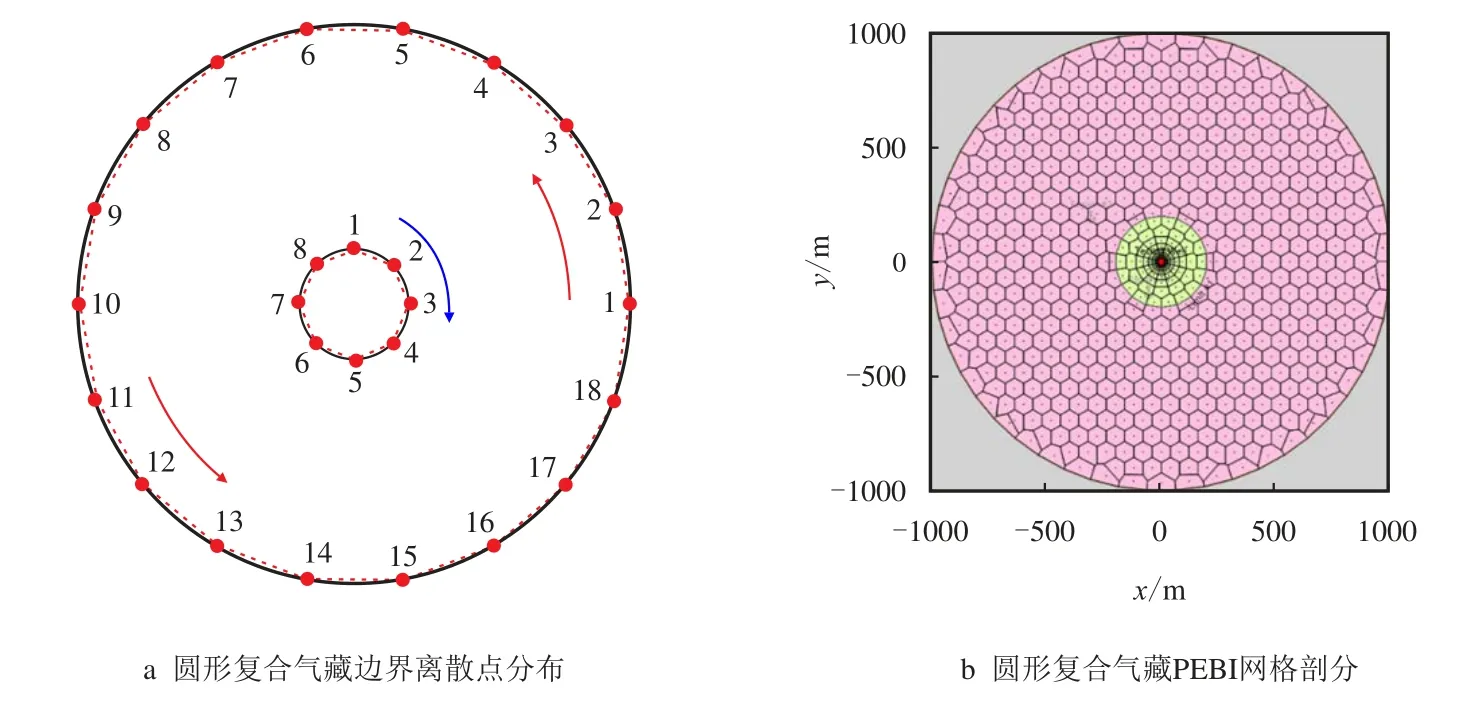
图5 圆形复合气藏边界元及PEBI 网格剖分结果示意图Fig.5 Diagrams of boundary discrete element for BEM and PEBI grid for circular composite reservoir
分别采用商用Saphir 数值试井模块和源函数法获得该模型的解,对比发现,本文方法获得的结果与半解析法和PEBI 数值解法获得的结果完全一致,如图6 所示。
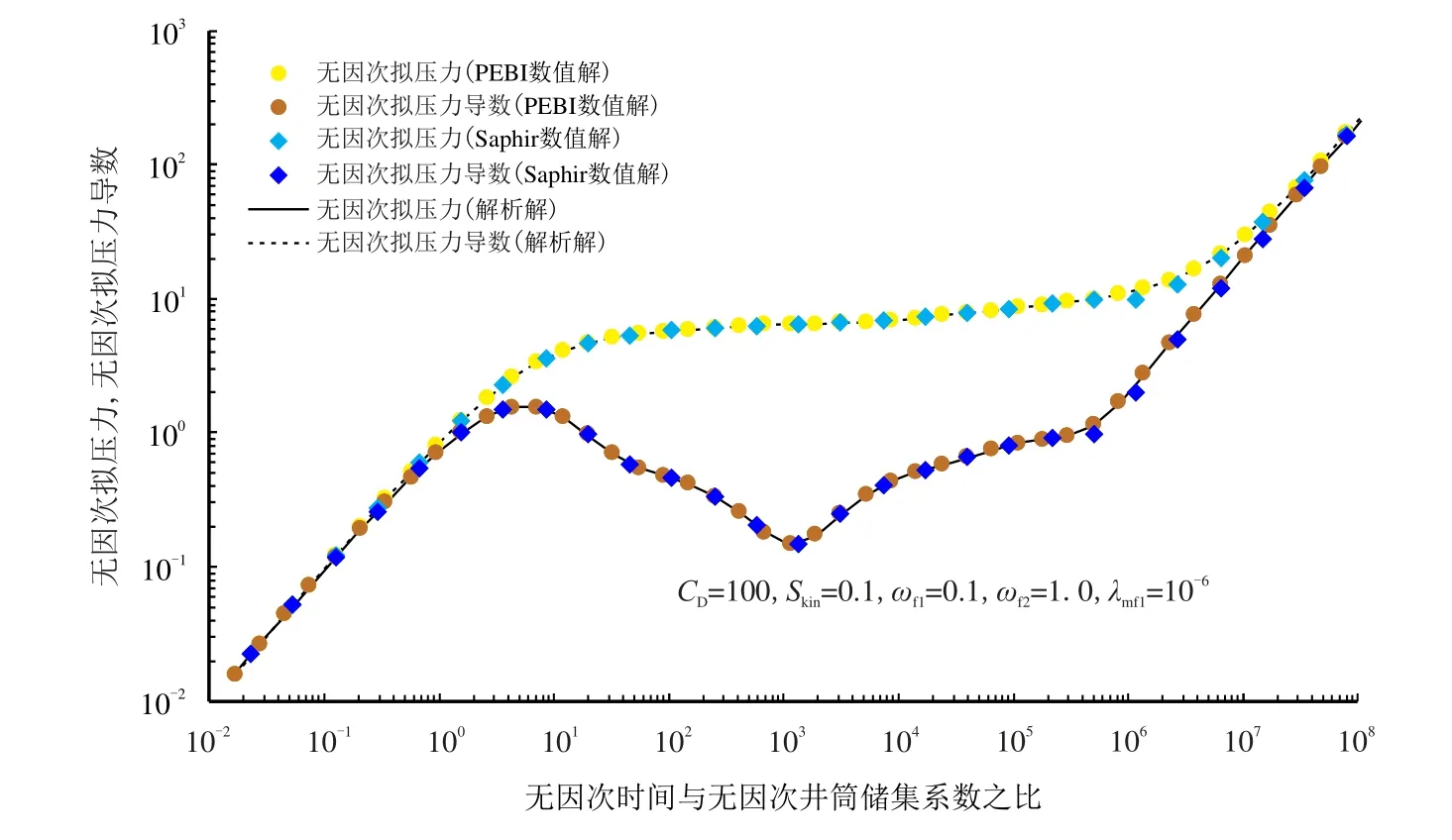
图6 不同求解方法的圆形复合气藏直井压力对比Fig.6 Results comparisons of different solving methods for circular composite gas reservoir
2.2 曲线特征与影响因素分析
利用本文建立的模型和方法对不同影响因素下的气井试井曲线进行分析。
以川西北双鱼石区块栖霞组气藏储层基础物性参数为背景给定的参数表如表1 所示,利用这些参数代入前文建立的边界元理论计算模型,可计算出不同时刻、不同参数条件下的气井压力动态变化情况。

表1 储层基础物性参数表Tab.1 Parameters for gas reservoir
图7 为不同外区基质系统向天然裂缝系统窜流系数下的气井井底无因次拟压力及其导数曲线示意图,可以看出,窜流系数主要影响试井曲线窜流凹子发生的时间,窜流系数越大,基质向裂缝系统补充能力越强,窜流凹子发生的时间越早。本实例中内区基质-裂缝系统窜流系数没有发生改变,早期窜流凹子未发生变化;当外区窜流系数为10−7时,外区窜流发生在内区向外区过渡阶段,导致外区窜流凹子被掩盖。
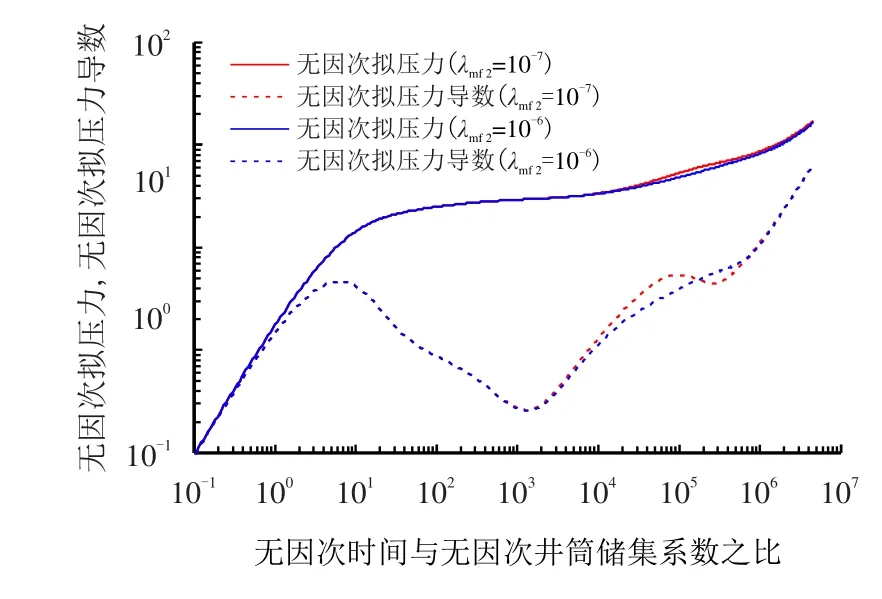
图7 不同外区基质-裂缝窜流系数对试井曲线的影响Fig.7 Effects of well test curve at different matrix-fracture interporosity flow coefficient in outer region curves
图8 为内区裂缝系统储容比对气井压力动态曲线的影响图。由于裂缝系统储容比代表裂缝孔隙系统的储集能力占系统孔隙的比值,储容比越大,裂缝系统储集能力越强,在拟压力导数曲线上表现为窜流凹子越窄,深度越浅,窜流发生的时间相对较晚。
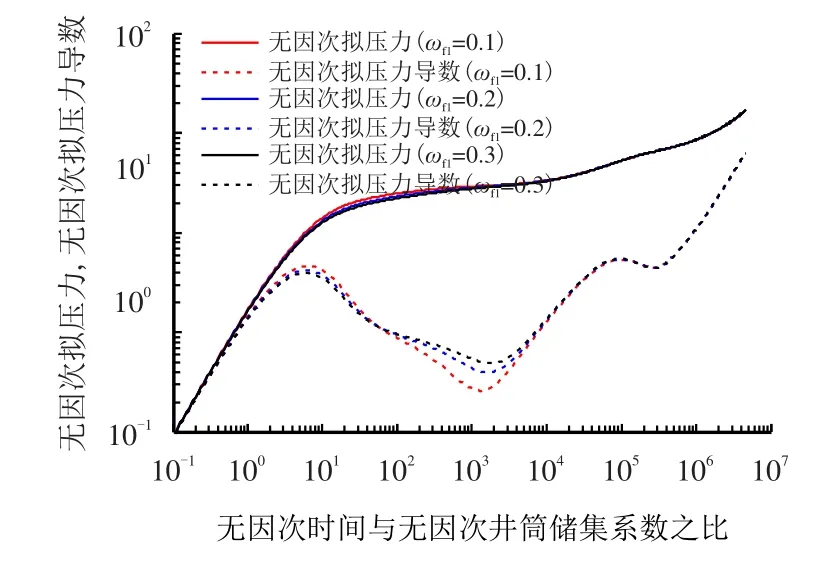
图8 不同内区裂缝储容比对试井曲线的影响Fig.8 Effects of storitivity between inner and outer region on well test curves
图9 为不同内外区裂缝系统流度比对气井压力动态曲线的影响图。内区与外区流度比越大,表明内区的流动能力越强,在无因次拟压力导数曲线上表现为拟压力导数曲线到达外区流动阶段后的值越大,曲线位置越高。
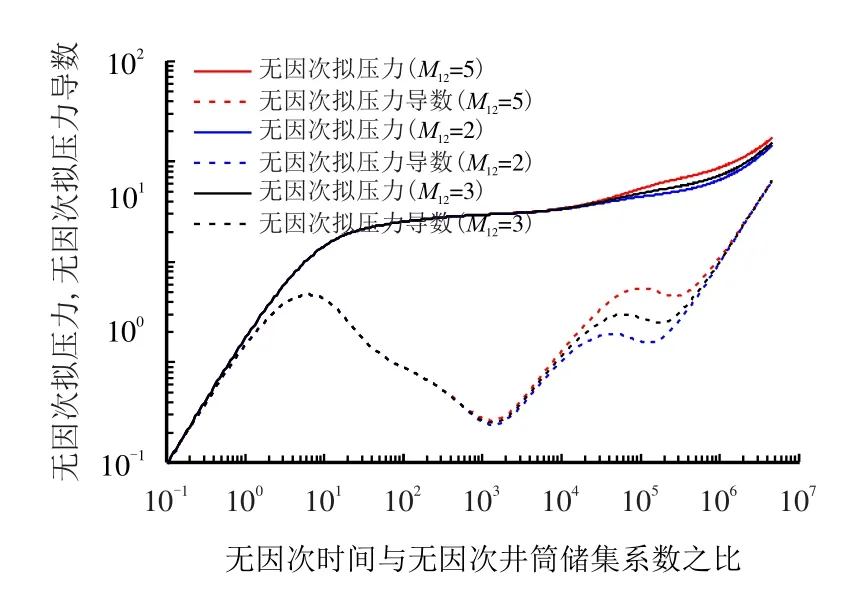
图9 不同内外区流度比对试井曲线的影响Fig.9 Effects of mobility ration on well test curves
图10 为双重介质复合气藏不同外边界形状物理模型示意图,相比传统的解析法,本文提出的边界元法不仅能够处理规则边界储层流动问题,对于任意形状的复杂边界储层不稳定渗流模型均可以进行快速求解,相比Saphir 数值试井模块具有精度高、快速的特点。
与图10 对应的不同边界形状对气井试井曲线的影响如图11 所示。
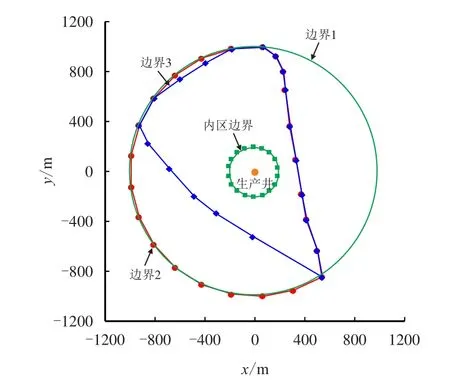
图10 双重介质复合气藏不同外边界形状物理模型示意图Fig.10 Schematic of dual-porosity composite gas reservoir with different outer boundary
图10 结合图11 可见,边界形状越不规则,压力波到达边界的时间越短,边界反映时间越早。受边界作用影响,外区窜流凹子被掩盖,导数曲线上则表现为均质气藏的特征,因此,对于断块发育或井离边界较近的井在进行试井模型的选取时需充分结合储层地质特征进行模型选择。
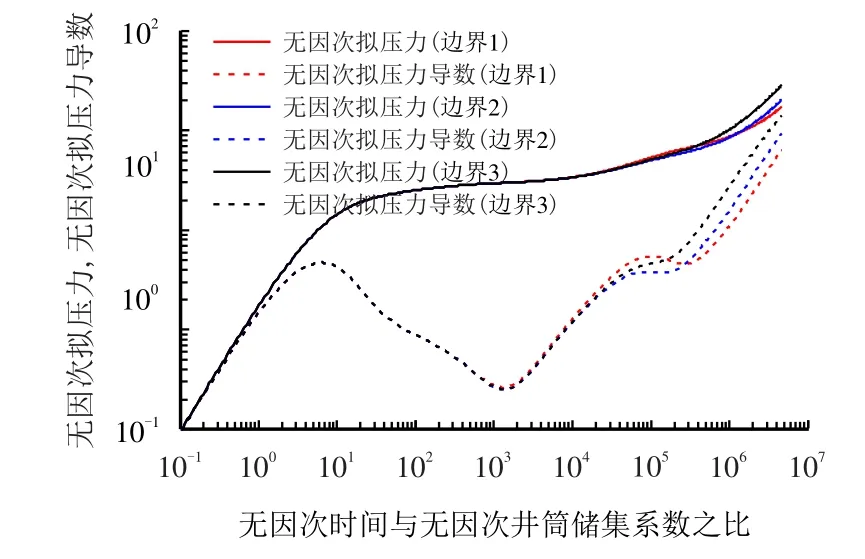
图11 不同边界形状对气井试井曲线的影响Fig.11 Effects of outer boundary on well test curves
3 实例应用
双鱼001–1 井位于双鱼石栖霞组顶界地震反射构造东北高点,见图12。

图12 川西北双鱼石区块栖霞组气藏顶界构造井位图Fig.12 Well location of carbonate gas reservoir in Qixia Formation,Shuangyushi Area,northwest Sichuan Basin
双鱼001–1 井是双鱼石构造的一口滚动评价井,完钻井深7 510.00 m,井底温度157.52◦C,其钻遇的栖霞组储层测井解释成果平均孔隙度3.45%,平均含水饱和度12.3%,产层中部垂深7 171.65 m,原始地层压力95.32 MPa。该井2017 年11 月投产,目前生产稳定,不产地层水。
2019 年3 月,双鱼001–1 井栖霞组试井现场工作历时11 d,试井解释采用的基础数据见表2。试井关井前产量控制稳定,关井期间井口密闭不漏,录取的压力、温度数据质量可靠,试井分析获得预期的压力响应特征,试井解释成果有充分依据;本次关井压力恢复较快,表明地层能量充足。

表2 双鱼001–1 井栖霞组试井解释采用的基础数据Tab.2 Basic parameters of Qixia Formation in Well Shuangyu001–1
基于双鱼001–1 井前期地质认识,以断层和储层含气边界作为模型边界,基于本文建立的边界元理论和观测气井压力测试导数曲线形态,选取复合模型对气井压力恢复测试数据进行拟合分析,采用的模型示意图如图13 所示。
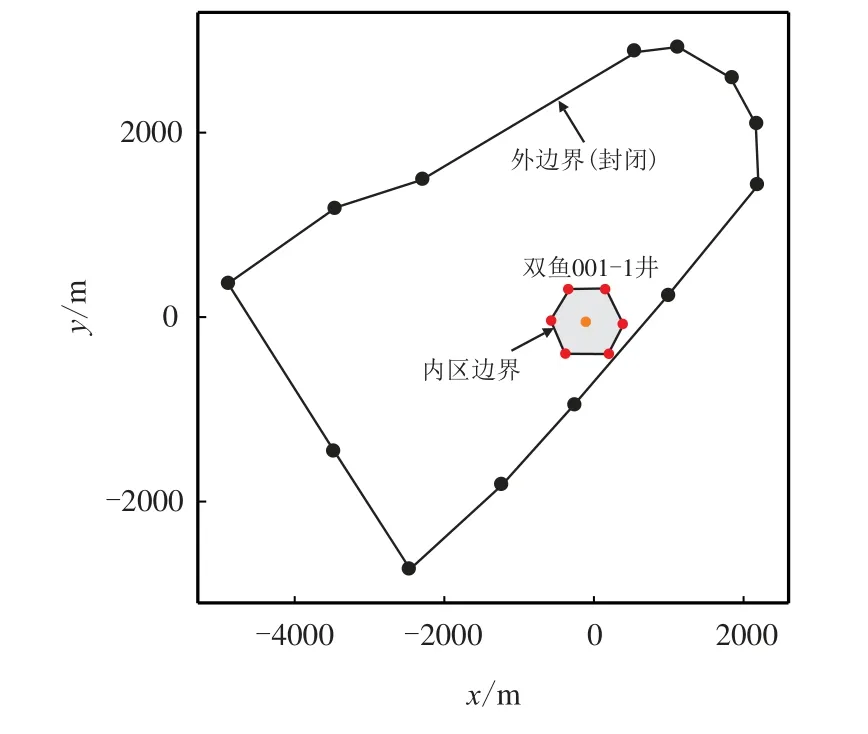
图13 基于边界元的双鱼001–1 井试井模型物理示意图Fig.13 Physical model of Well Shuangyu001–1 with BEM
结合图版和实测数据,优化调整试井模型参数,得到的试井解释结果如表3 所示。

表3 双鱼001–1 井试井解释结果Tab.3 Results of well testing interpretation on Well Shuangyu001–1
解释过程中,使用的压力恢复试井双对数拟合分析图如图14 所示,压力恢复试井时间叠加拟合分析图如图15 所示。
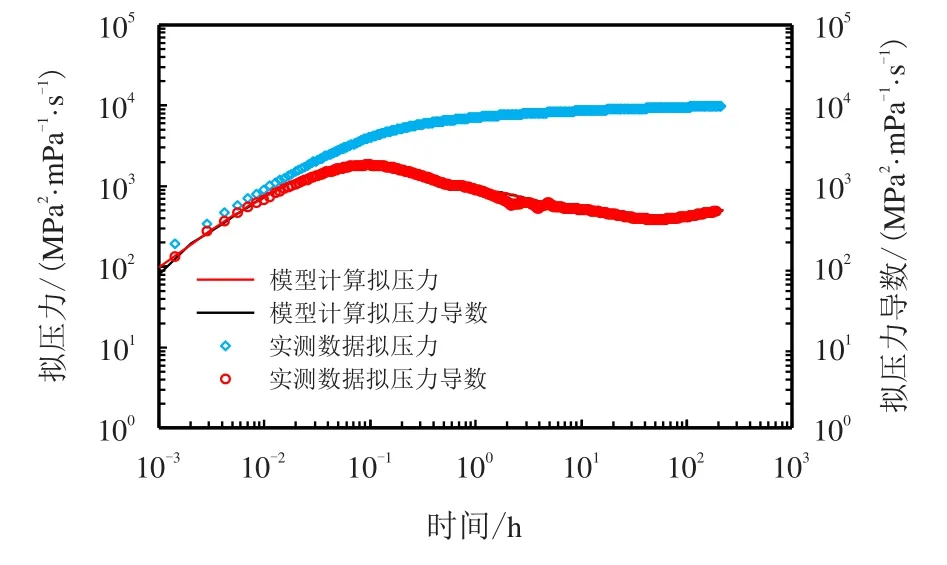
图14 双鱼001–1 井压力恢复试井双对数拟合分析图Fig.14 Fitting results of Well Shuangyu001–1 log-log curves
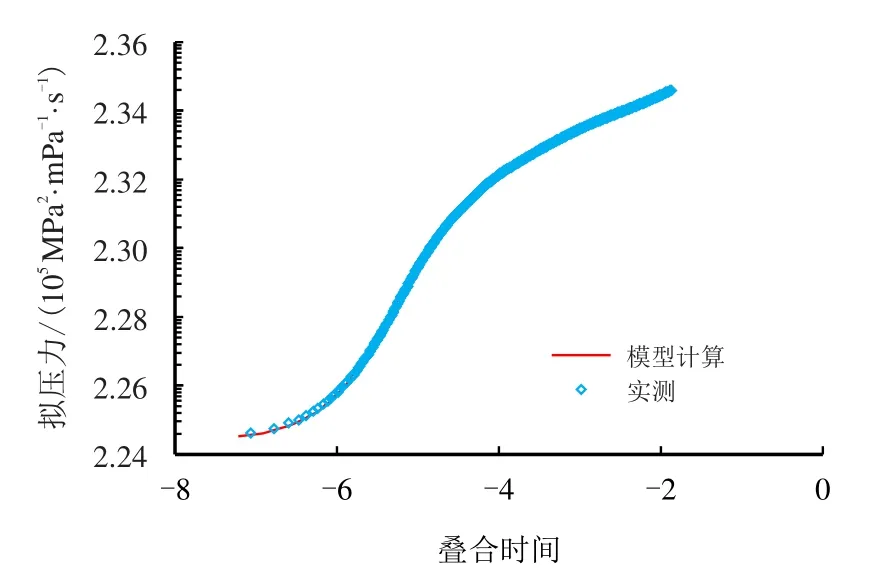
图15 双鱼001–1 井压力恢复试井时间叠加拟合分析图Fig.15 Fitting results of pressure history for Well Shuangyu001–1
4 结论
1)采用边界元理论与方法,构建了双重介质拟稳态窜流复合气藏模型任意外边界直井不稳定渗流的边界元模型,采用高精度边界元数值求解算法,系统分析了不同参数对压力动态响应特征的影响。
2)分析了复合气藏复杂外边界对气井压力动态曲线的影响,结果表明由于气井距离边界距离较近,导致许多流动特征被边界所掩盖,给常规试井解释理论与方法带来挑战,因此,对于双鱼石复杂构造气藏试井解释需要考虑边界的影响。
3)针对川西北双鱼石栖霞组构造高部位生产井双鱼001–1 井的压力恢复测试数据,基于储层真实含气和构造外边界,考虑早期储层酸化形成的复合区域,运用该模型求解方法,取得了较为可靠的解释结果。
符号说明
