基于宽频子波的检波组合目标函数优化方法

2023-05-10彭更新徐凯驰刘福烈李勇军

西南石油大学学报(自然科学版) 2023年2期

彭更新，徐峰，徐凯驰，刘福烈，李勇军

1.中国石油塔里木油田公司勘探开发研究院，新疆库尔勒841000 2.西南石油大学地球科学与技术学院，四川成都610500

引言

检波器组合可以压制规则干扰和随机噪音，是地震采集中提升信噪比的有效方法[1]。检波器组合相当于一个空间方向滤波器，对不同角度入射的谐波分量根据其相位差异予以通放和压制[2]，相对增强地震反射信号，在低信噪比地区应用广泛[3-5]。进行组合参数设计有两点需要考虑，一是找到影响组合响应的所有参数，建立起这些参数与响应间的函数关系；二是找到一个合理的目标函数，优化求解组合参数。

针对组合能量响应分析及目标函数设计方面，前人已做过许多研究，并取得了较好的应用效果，Parr 等[6]研究了正弦信号的组合能量响应，固定5 个检波器，以最大组合能量响应为目标，确定了检波器接收最佳入射角范围；Holzman[7]从组合能量响应符合压制带内多极值相等原则，设计了切比雪夫多项式加权组合，其具有较窄的压制带以及较少的检波器组合数量；Rietsch[8]改进了切比雪夫多项式权系数计算公式，在保证计算精度的前提下，提升了计算效率；Kerekes[9]以组合能量响应的旁瓣与陷波点位置不变为前提，以陷波点振幅最低及旁瓣振幅最高为目标函数，采用空间卷积的方式进行了组合设计；Craig 等[10]提出以地震道组合前后频率相关性作为衡量组合效果的目标函数，并通过现场试验比较了不同组合方式的实际效果；Timothy 等[11]在Perth 地区研究了背景噪声相干性与组内距的关系，基于传感器之间的平均相关系数探索最佳检波器间距。徐峰等[12]在进行震源组合设计时给出了一种以激发效率为目标函数的组合参数设计方法。

由于地表组内高差、波的非平面入射等因素，组内各点信号的到达时间往往不同，不将组内时差纳入组合参数考虑，往往得不到较好的组合效果。

在组合时差方面，Johnson[13]根据近地表噪声与有效波到达检波器的时差，由检波器位置确定延时量，通过延时叠加提升信噪比；King 等[14]采用选取参考道与各独立地震道做互相关的方法确定延时量，用于地震数据组合叠加；Levy[15]研究了自动相位校正法，Eisner 等[16]提出了相位分解法，这两种方法都是为了准确得到各道波组旅行时间，更好地匹配有效波形；Mao 等[17]通过线性化波形反演技术同时估计组合的延时量与权系数；Bagaini[18]将各检波器延时量、检波器接收时差通过一个系数矩阵建立方程，通过最小二乘法求解延时量，通过实验证明在低信噪比条件下也能比较准确地估计延时量；魏继东等[19]研究了检波器组内高差对高频信息的压制效果；Panea[20]对相位变化情况下的室内组合技术进行了分析，指出单道接收的室内组合法可在组合前通过相位校正处理解决组合道集内相位变化对地震反射波产生影响的问题；蓝阳等[21]基于波束形成理论讨论了余弦加权组合方式在室内组合方面的效果。

分析以往的研究成果，对组合响应以及相关的组合数目、组内距、能量加权系数和组合时差等组合参数都已有过较为详细的探讨，但在目标函数的研究方面仍存在一些不足，表现在建立的目标函数主要借助于组合能量响应零点位置、压制带幅值、压制带极值与通放带极值比等方面，这可能导致评价组合接收效果不全面。无论有效信号还是噪声都是分布在一个连续的空间上的，因此，建立包含区间统计能量的目标函数更有意义。

此外，现有理论中一般假定地震波为单频简谐波[22]，与实际地震子波有一定差异。本文借鉴雷达相控理论，推导了宽频子波的组合能量响应，根据干扰波和地震反射波在分布范围上的差异，统计了地震反射波区间和干扰波区间的能量，建立了具有统计意义的多种组合接收目标函数进行多参数寻优，利用组合前后的地震记录及其频谱、AVO 特性对各目标函数进行对比，从而得到更为合理的组合接收目标函数。

1 组合能量响应

图1 是检波器组合示意图。

图1 检波器组合示意图Fig.1 Schematic diagram of detector combination

组合叠加后的波场可表示为[23]

对式（1）进行欧拉分解，取模，得到

当ψ=0 时，到达的简谐波间没有相位差，组合输出可以提升N倍波场能量。

式（2）与式（3）相除可得归一化后的能量响应因子E

固定N=12，d=6 m，v=800 m/s，f分别取10、20、30 及60 Hz，绘制与入射角相关的能量响应因子，如图2 所示，可见曲线随频率和入射角度变化而变化，存在若干极值点与零点。

图2 不同频率简谐波组合能量响应因子曲线Fig.2 Energy response factor curve of simple harmonic combination of different frequencies

对式（4）求偏导，并令其等于0，可得

极值点由式（6）给出

其解为

当θext=0 时，式（4）取值1，为主极值，当θext≠0时，次极值可由式（8）表示

在地下半空间的接收角度区间θ ∈[−90◦,90◦]内，次级极值点数目由N、f、d及v 共同决定，总数不超过2N fd/v–2 个。极值点的值只与m和N有关，组合个数越多，m值越大（入射角越大），极值越小。

再来考察零点位置，零点满足使式（4）分子为零，分母不为零的条件，即

在地下半空间的接收角度区间内，零点同样与N、f、d及v 有关，共有不超过2N fd/v 个。

能量响应因子曲线代表简谐波通过组合系统后能量被通放（或压制）的程度，可见随空间入射角增大，组合通放能量震荡式减小，理论上能量值会有2N fd/v 次机会被压制为零。这就是组合能够压制高角度传播噪音的基本原理。

理想情况下，希望组合能够对低角度的入射波（有效信号成分）完全通放，对高角度的噪声完全压制，如图2 中的理想响应曲线，但实际情况下很难做到绝对的通放与压制。一般定义能量的0.707倍作为组合通放与压制带的分界点[1]。组合参数的设计就是要让角度小于分界点的范围内保留更多能量，大于分界点的范围内压制更多的能量。

图2 中不同频率成分响应曲线的0.707 位置对应的角度是不同的，这就为组合参数设计带来了困难—基于地震子波的宽频性质，选择任何一种简谐成分似乎都不合理。基于傅里叶的分析，地震子波是多种频率成分的简谐波以不同能量的叠加，改进式（4），引入频率加权系数，得到式（10）

如果地震子波为Ricker 子波，则A(f) 可用式（11）的Ricker 子波频域表达[24]。若子波未知，可对实际地震数据做频谱分析，取归一化振幅谱代替。

在推导式（1）时作了平面简谐波假设，但由于各检波器存在高程差等因素，组合时各子波的波前面不一定是平面，即子波到达组合各检波器位置时本身可能存在时差（延时量）∆tn，这个时差应该追加在等间隔时差后面，即ndsinθ/v+∆tn。

另外，各子波本身携带的能量也可能不同（各检波器的接收振幅可调节），所以组合时还应该将能量加权系数αn考虑进来。

由此得到新的归一化能量响应因子表达式如式（12）所示，由于能量加权系数αn和延时量∆tn的存在，复指数的模无法简洁地展开，式（13）分别为复数的实部与虚部。可以看出，能量因子是组合内检波器个数N、组合内相邻检波器之间的距离d、平面简谐波速度v、能量加权系数αn、延时量∆tn及入射角度θ 的函数，同时与子波的频率成分有关。

式（14）为一种加权系数的计算方法[25]，是由引入加权系数后的式（1）经傅里叶反变换得到，在给定的相位区间[ψ1,ψ2]内对期望响应E(ψ)做积分得到加权系数。该加权系数为复数，在组合个数较多、组内距不大的情况下逼近期望响应的效果较好。

图3 给出了3 条对比曲线，分别是30 Hz 单频简谐成分的式（4）、采用30 Hz 主频Ricker 子波振幅谱加权的宽频叠加式（10）以及采用傅里叶能量加权系数的式（12）。

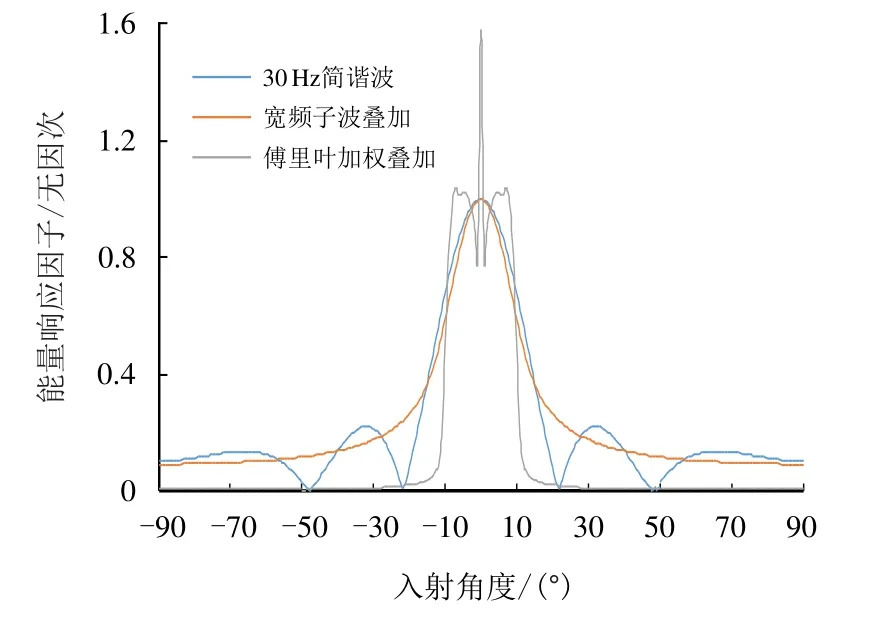
图3 宽频子波组合能量响应因子曲线Fig.3 The energy response factor curve of broadband wavelet combination

从图3 可以看到，宽频子波叠加在低角度区域和简谐波基本一致，区别在高角度区域不再有零值点，能量平滑减弱，这是因为叠加过程不同频率成分的零点位置相互掩盖所致。在将各检波器的能量系数考虑进来后，曲线更逼近期望的“门”式响应，对高角度区域的能量压制更为明显。

2 组合目标函数设计

响应关系建立之后，组合参数设计的下一步工作就是要建立一个优化求解的目标函数。

检波器接收到的地震信号可以分为4 类：I 类为震源激发，经目的层反射后的有效信号；II 类为震源激发，非目的层（如浅层非均质体、强波阻抗反射界面）反射的干扰信号；III 类为地表风吹草动、汽车和人行走等产生的微震，传至目的层反射的干扰信号；IV 类为地表微扰动沿地表直传检波器的干扰信号。

图4 是组合接收示意图，可以看出，噪声主要来源于近地表，入射角较大；当勘探目的层较深时，有效信号的入射角较小。

图4 组合接收示意图Fig.4 Schematic diagram of combined reception

建立目标函数前首先要确定有效信号最大角度θmax，精确地获取该角度较困难，通常采用式（15）进行计算

之后，需要分别统计[−θmax,+θmax]区间内的有效信号能量和范围外的噪声能量。

根据组合压制噪声，提高地震资料信噪比的目的，可设计4 种目标函数用于确定组合参数：1）噪声区能量最小，目标是追求最大的压制效果；2）有效信号区能量最大，目标是追求最佳的有效波保护；3）噪声区能量与检波器接收总能量的比值最小，目标是平衡压噪与有效信号保护，侧重噪声压制；4）有效信号区能量与噪声区能量的比值最大，目标是强调有效信号与噪声的相对强弱关系。

在影响目标函数值的若干变量中，平面简谐波速度v 由地质结构决定；频率成分加权系数A(f)与地层中传播的子波有关；有效信号最大角度θmax由观测系统或实测数据决定，能够在检波端予以调整的参数只有N、d、αn及∆tn。

因此，组合参数设计就是以P1、P2、P3及P4中的某一个为目标函数，寻优求解这4 个变量的问题，求解过程可以采用贪婪算法以得到全局最优解，但较费时；也可以采用某种数值优化算法，在给定合理的解初值情况下，收敛速度很快，本文求解采用粒子群算法。

3 数值模拟

设计一个如图5 所示的理论地质模型。模型含3 套水平地层，首先，将震源放置在模型地表中央位置，检波器排列铺满地表，采用主频30 Hz 的雷克子波进行波动方程正演，得到图6a；然后，改造模型，在地表下15 m 处均匀分布一层散射点，再次完成正演，同时加入随机噪声，得到图6b。图6a 不含任何噪声成分，作为分析比较的参照；图6b 含有散射噪声和随机噪声，作为后续组合处理的原始数据。

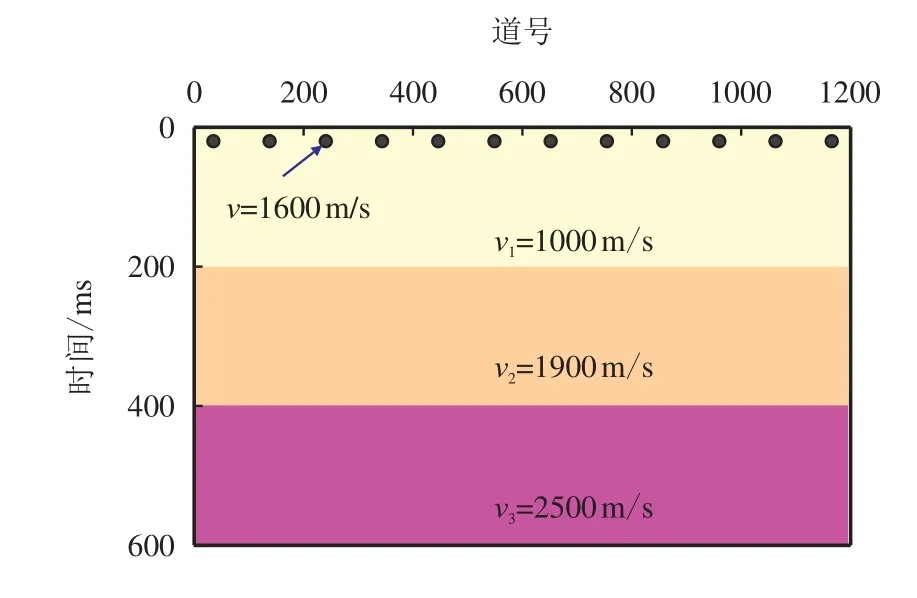
图5 3 层地质模型Fig.5 Three-layer geological model

图6 不含噪与含噪单炮正演记录Fig.6 No noise and noisy record

根据模型参数，使用式（15）计算有效信号最大角度θmax=26.6◦，4 组目标函数的优化结果见表1。

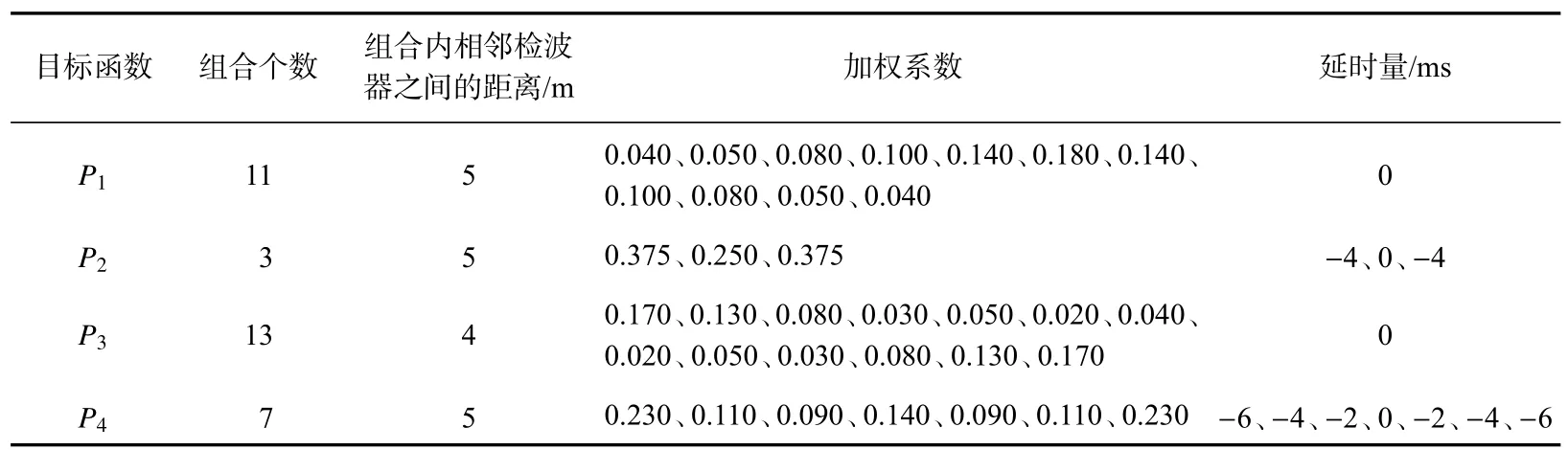
表1 4 种目标函数的优化结果Tab.1 Optimization results of four objective functions

将表1 参数代入式（12），得到4 组目标函数对应的组合能量响应如图7 所示，红线为±26.6◦的有效波区间。由图7 可以看出，在有效波区间内，通放能力排序为P2、P4、P3及P1；在区间外，压制能力排序为P1、P3、P4及P2。

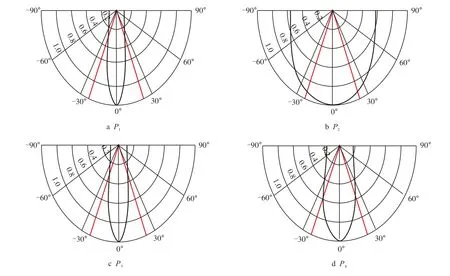
图7 不同目标函数的组合能量响应Fig.7 Combined energy response of different objective functions

按表1 参数对图6b 数据进行组合，得到图8，将图8 各图与图6b 相减，得到图9，图9 为组合压制掉的噪声部分。

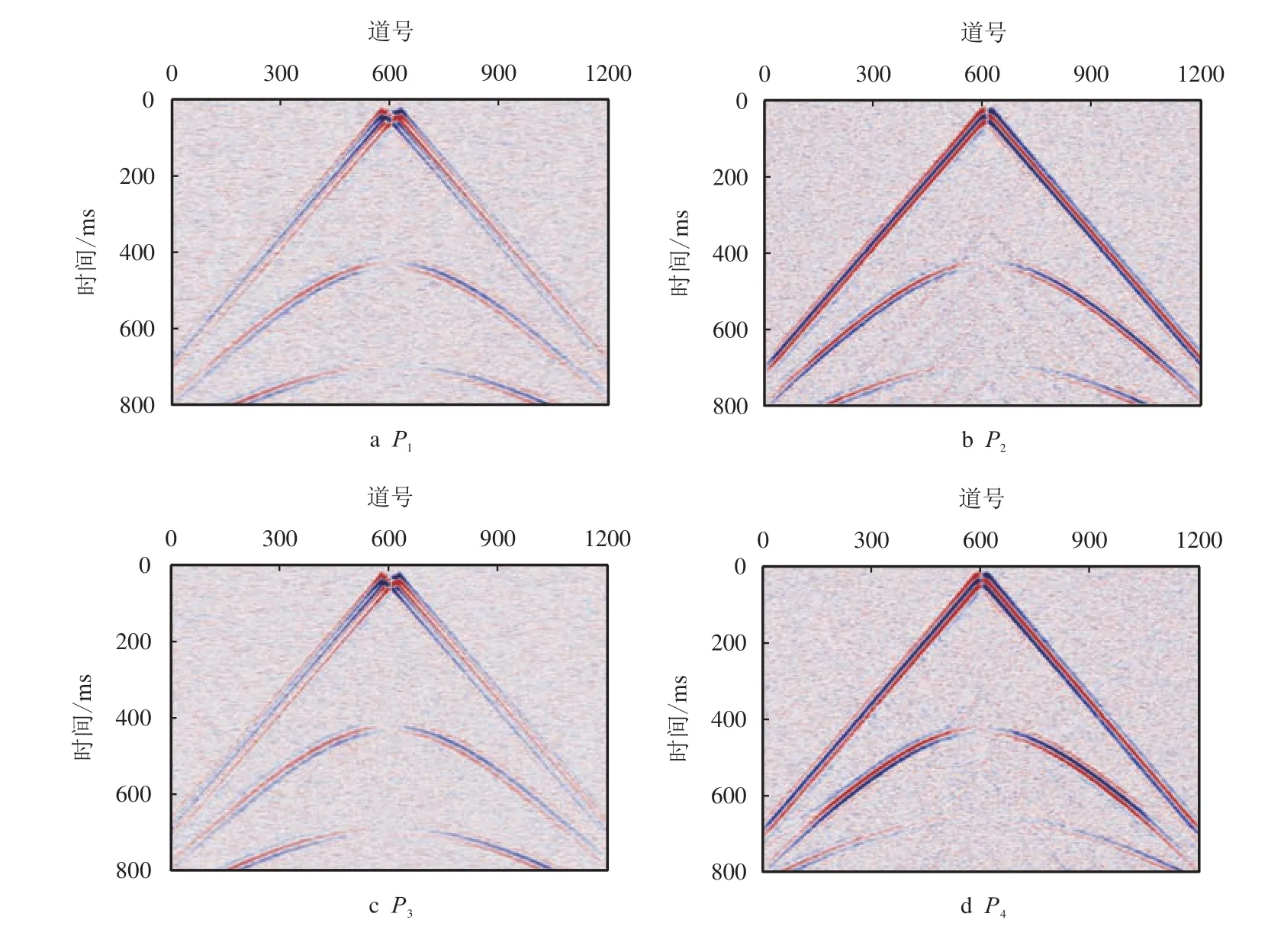
图8 不同目标函数的组合结果Fig.8 Combination results of different objective functions

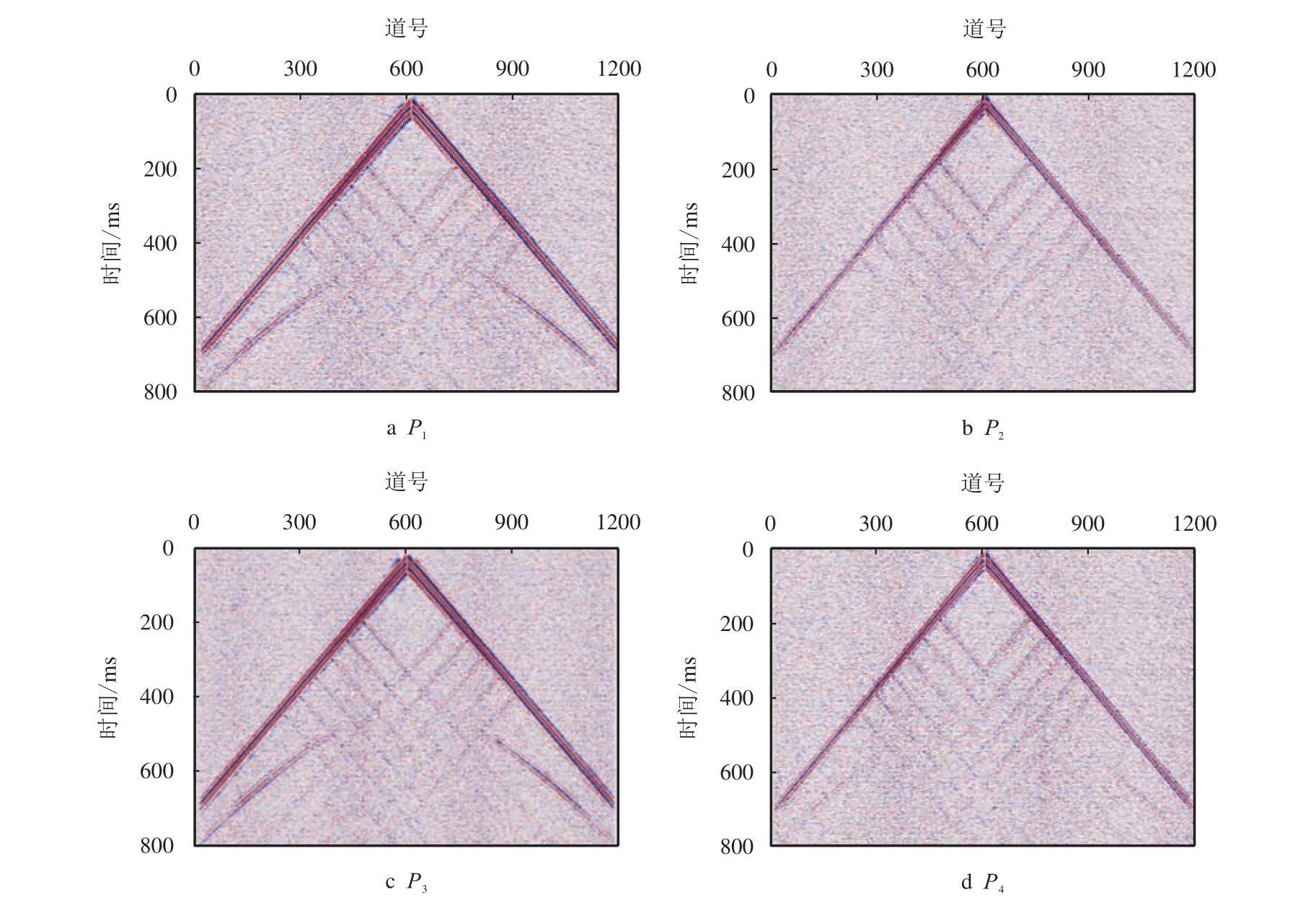
图9 不同组合压制的噪声Fig.9 Noise suppressed by different combinations

以噪声区能量最小（P1）和噪声区与总能量比值最小（P3）为目标函数设计的组合参数对于散射干扰压制较好，但有效波损伤较为严重，这是因为二者的设计目标主要考虑噪声压制。以有效信号区能量最大（P2）为目标函数设计的组合参数对有效信号损伤较小，但对于散射噪声压制不完全。以有效信号与噪声区能量比值最大（P4）为目标函数设计的组合参数能较好地平衡有效波损伤与散射干扰压制。

取4 组组合后记录及图6a 参考记录做频谱和AVO 分析，如图10 和图11 所示。

图10 各组合记录频谱曲线Fig.10 Record spectrum curve of each combination

图11 各组合记录AVO 曲线Fig.11 Record AVO curve for each combination

从图10 和图11 可以看出，以有效信号区能量最大（P2）为目标函数设计的组合参数优先保护了有效波，其频谱分布及AVO 曲线特征最为逼近原始数据；以有效信号与噪声区能量比值最大（P4）为目标函数设计的组合参数，存在低通滤波效应且远偏的能量畸变明显；两种优先考虑噪声的目标函数（P1、P3）低通滤波效应最为明显，AVO 畸变严重，不可取；相比较而言，只有P2综合考虑了有效波保护与噪声压制，是一种较为理想的方案。

4 实例分析

图12 为某工区的实际数据，由于在野外采用单一震源接收（不进行野外检波组合），记录中存留了相关、随机、异常振幅等大量噪声，需要在室内进行压噪处理。

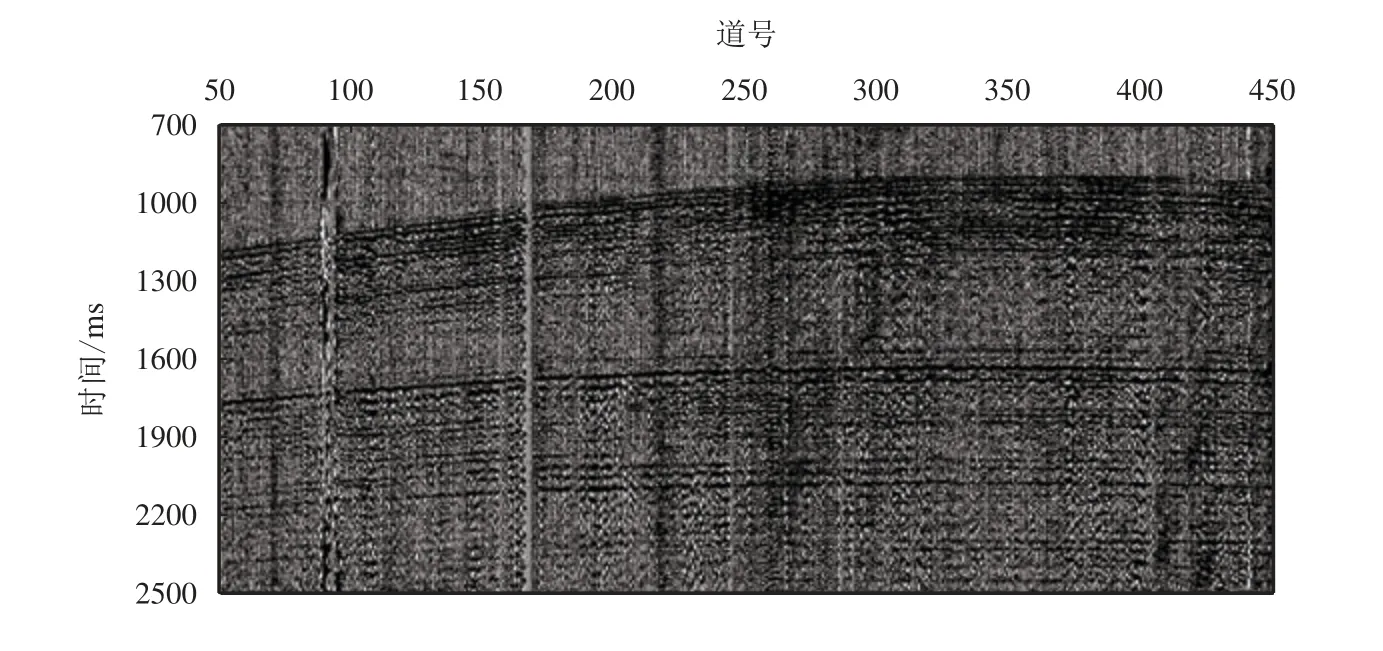
图12 某工区的实际数据Fig.12 Actual data of a work area

工区的三维采集参数为36 线-720 道-20 炮，炮点间隔与检波点间隔很小，都为10 m，非常有利于应用室内组合技术。

组合处理前需要对数据先进行静校正处理，再利用式（12）计算各空间角度上的能量值，利用式（15）计算有效信号最大角度θmax=30◦，使用式（16）与式（17）计算有效信号和噪声区间的能量，然后使用式（18）∼式（21）来优化计算式（12）中的N，d，αn和∆tn。

图13 为以P1∼P4为目标函数得到的组合结果。与理论分析类似，P1与P3方法对压制噪声更有利，尤其是P1，组合后图中基本看不到随机、相关和异常能量噪声（图13a）；而P2和P4方法可以更有效地保护反射的连续性和能量变化。

图13 实际采集地震数据的组合结果Fig.13 Combination result of actually acquired seismic data

图14 展示了各方案压制掉的噪声成分。对照图7，当使用P1与P3方法的时候，通放带内（图7中的红线）的能量曲线迅速衰减，实际的通放角度非常窄，相对高角度入射的浅层反射波很容易被压制，反映在图14 中就是大量的有效信号被当作噪声压制掉了。与之相对应，P2和P4方法压噪能力变弱，但较好地保护了有效信号，更进一步比较二者，P2保护有效信号更有利，P4压制噪声能力更强。

图14 实际数据不同组合方式压制的噪声Fig.14 Noise suppression by different combinations of actual data

同样的结论也可以在图15 所示的组合前后反射层频谱曲线及能量统计中得到。P2考虑有效信号保护更多一些，其频谱与AVO 响应曲线与原始数据曲线最为接近；P4压制了更多的噪声，谱曲线在高频段下降，AVO 曲线也整体下降，但保持了与原始数据曲线大致平行的关系，也就是说它并没有显著改变AVO 关系；P1与P3显著改变了频谱和AVO曲线，不建议采纳。