相关随机变量拉丁超立方抽样及隧道掌子面稳定性概率分析

0 引言

随着可靠度理论的不断发展,可靠度设计在岩土工程的应用越来越广。可靠度设计方法包括一次二阶矩法、一阶可靠度法、响应面法、数据表法和蒙特卡洛法等。其中,蒙特卡洛法是最为直接和准确的方法[1-2]。蒙特卡洛法采集的样本可通过有限元计算得到失效概率,分析结果可作为其它方法计算结果的唯一验证[3-9]。然而,蒙特卡洛法的计算成本较高,对于失效概率较小的问题,有时几乎不可能实现。

M. D. MCKAY等[10]在1979年指出拉丁超立方抽样技术可降低计算消耗,该技术具有分层均匀、抽样少的优点。具体计算步骤:① 确定抽样样本数N;② 将变量的累积分布分成相同的N个小区间,即将变量累积分布(0,1)区间均分成N段,使得每个区间有相同的概率;③ 从N个区间段中分别随机抽取一个值,将抽取的N个值分别通过变量的分布反函数映射为变量的样本,共计得到N个样本。随机变量的拉丁超立方抽样原理如图1。图1(a)表示将样本的概率分布范围划分为5个概率相等的区间,每个区间采集一个样本点;图1(b)表示2个独立样本经分层抽样后的组合情况,2个变量在任何一个分割的概率区间只出现一次,以保证所采集的样本最具代表性。拉丁超立方抽样保证了尾部层中的样本也会被抽取,而这些样本对于失效概率计算来说是非常重要的;拉丁超立方抽取样本数量越多,分层就越多,极端的尾部值就更容易被抽取。

图1 拉丁超立方抽样原理

拉丁超立方抽样假定所有随机变量是相互独立的,而在岩土工程中很多参数往往具有相关性,因此,无法直接进行拉丁超立方抽样,需要进行相应的变换。具体变换方式可参考相关随机变量蒙特卡洛抽样。常见4种不同类型相关随机变量蒙特卡洛抽样的实现步骤如下:

1)对于均为正态分布的多维相关随机变量,可基于协方差矩阵的Choleshy因子分解将其转换为独立标准正态分布的随机变量进行蒙特卡洛抽样[11]。

2)对于均为对数正态分布的多维相关随机变量,可将其转换为正态分布的多维相关随机变量进行蒙特卡洛抽样,转换后协方差矩阵跟随改变[12]。

3)对于非正态分布的多维相关随机变量,可采用Nataf变换分2步将其转换为独立标准正态分布的随机变量进行蒙特卡洛抽样[13]。

4)对于已知秩相关矩阵的多维相关随机变量,可将其转换为具有相同秩相关矩阵及相同维度的标准正态分布的相关随机变量,再根据相关随机变量的边缘分布生成所需要的样本,使得每个维度上相关随机变量样本从大到小的排序与对应维度上标准正态分布相关随机变量蒙特卡洛抽样样本从大到小的排序一致,从而实现秩相关随机变量的蒙特卡洛抽样[14]。

笔者参考相关随机变量蒙特卡洛抽样的实现,结合拉丁超立方抽样原理,采用Python语言编程实现了上述4种类型的相关随机变量拉丁超立方抽样。

1 相关随机变量拉丁超立方抽样原理及实现

1.1 相关随机变量Pearson相关

1.1.1 相关随机变量的正态分布

正态分布进行线性变化后仍然是正态分布,且相关性不变,因此,任意满足正态分布的相关随机变量均可以通过标准正态分布的线性组合得到,表达式如式(1):

x=A·ξ+μ

(1)

式中:x为一组正态分布的相关随机变量;μ为各相关随机变量的均值矩阵;ξ为一组相互独立的标准正态分布变量;A为转换矩阵。

G. ZEROVNIK等[12]证明了V=AAT,其中V为相关随机变量x的协方差系数矩阵。又知V是一个对称的正定矩阵,可以通过Choleshy分解成2个矩阵的乘积,因此,只要得到V的Choleshy分解矩阵就可以求得矩阵A。

在Python语言中,使用numpy库实现Choleshy分解,得到A=np.linalg.cholesky(V)。如果是给出的相关系数矩阵R,则V=σRσT,σ为对角阵,对角线上的元素为各相关随机变量的标准差。所以,对x的拉丁超立方抽样可以转化为对独立标准正态分布ξ的拉丁超立方抽样。实现拉丁超立方抽样用到Python的scipy.stats中的qmc和norm。

1.1.2 相关随机变量的对数正态分布

对数正态分布拉丁超立方抽样与正态分布拉丁超立方抽样具有相似性,若xi服从对数正态分布,则lnxi服从正态分布,即

(2)

式中:xi为第i个相关随机变量;Aij为转换系数;ξj为第j个独立标准正态分布变量;μi为lnxi的均值。

令yi=lnxi

(3)

则,式(2)可以写成:

y=A·ξ+μ

(4)

可见,式(4)的形式同式(1)。

因此,一组满足对数正态分布的相关随机变量的拉丁超立方抽样,可以转换为一组满足正态分布相关随机变量的拉丁超立方抽样。

根据G. ZEROVNIK等[12]研究,原对数正态分布x与转换后正态分布y之间的协方差系数的关系如式(5):

(5)

根据式(6)可以求得转换后yi的均值:

(6)

式中:E(yi)为第i个y变量的均值;E(xi)为第i个x变量的均值;D(xi)为第i个x变量的方差。

得到了正态分布y的A与μ,后续进行拉丁超立方抽样的计算步骤与正态分布的拉丁超立方抽样一致。得到相关随机变量yi的样本后,通过xi=eyi转换,即得到相关随机变量x的样本。

1.1.3 相关随机变量的非正态分布

LIU Peiling等[15-16]提出的Nataf转换法,将非正态分布转换到标准正态分布空间下,只需要知道变量的边缘分布以及变量间的相关系数,即可以把原始分布空间转换到独立标准正态空间。Nataf转换分2步:①将原始空间转换成相关的标准正态空间;②将相关的标准正态空间转换成独立的标准正态的空间,这可通过正态分布相关随机变量的拉丁超立方抽样来解决。

原始空间向相关的标准正态空间转换的操作为:输入一组相关随机变量X=(x1,x2,…,xn),若相关随机变量xi(i=1,2,…,n)的概率密度函数fi(xi)和累积密度函数Fi(xi)已知,通过等概率转换原则[15-16]可得:

(7)

式中:yi为一组标准正态相关随机变量Y=(y1,y2,…,yn)中的变量;Φ(·)、Φ-1(·)分别为标准正态累积密度分布函数和逆累积密度分布函数。

设X中任意2个相关随机变量xi、xj的相关系数为ρxixj,则

(8)

式中:μxi、μxj分别为xi、xj的均值;Δxi、Δxj分别为xi、xj的标准差;ρyiyj为yi、yj的相关系数。

在二元标准正态分布的联合概率密度函数数值计算中,式(8)的双重积分上下限选择[-4,4]就足够精确了[13]。在ρxixj、μxi、μxj已知的情况下,几乎不可能直接计算ρyiyj,因此,需采用数值计算法求解ρyiyj。当ρxixj>0时,具体步骤如下:

Step 1在[0,1]区间假设一个ρyiyj值。

Step 2将假设的ρyiyj值代入式(8),计算得到ρxixj。

当ρxixj<0时,在[-1,0]区间进行类似操作。

1.1.4 相关随机变量拉丁超立方抽样举例

以岩土工程中土体常见的黏聚力c、内摩擦角φ为例进行拉丁超立方抽样,抽取10 000个样本。均值c=10 kPa,φ=30°,标准差Δc=2 kPa,Δφ=2°,Pearson相关系数为-0.5。

分别进行正态分布相关随机变量抽样(c、φ均满足正态分布)、对数正态分布相关随机变量抽样(c、φ均满足对数正态分布)、非正态分布相关随机变量抽样(c满足对数正态分布,φ满足正态分布),抽样结果分布如图2,抽样参数c、φ概率密度如图3。

(a) 正态分布抽样

(b) 对数正态分布抽样

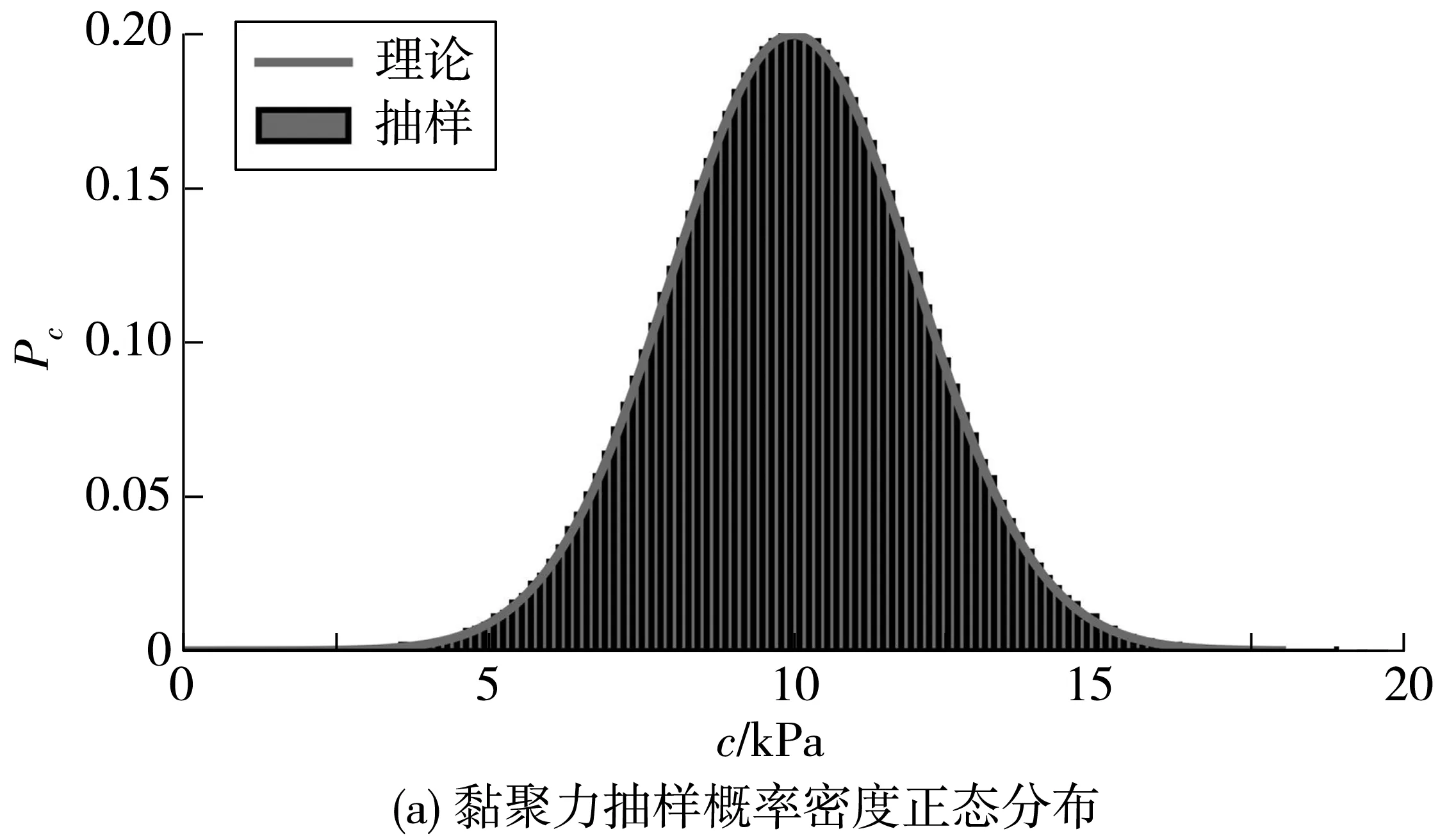
图3 正态分布、对数正态分布、非正态分布抽样概率密度

由图3可见,当Pearson相关系数不等于0时,c与φ的抽样概率密度分布曲线与理论概率密度曲线存在些许差异。分析原因,一方面可能是拉丁超立方抽样样本数量相对较少造成的;另一方面,可能是每个区间抽样的随机性造成的,尤其是在均值附近。

综上,随机变量Pearson相关的3种不同类型的拉丁超立方抽样保持了原变量的分布,在保持抽样精度的同时,大大降低了样本数量。

1.2 随机变量Spearman秩相关

Spearman秩相关系数只对变量的秩次大小进行线性相关分析,所以没有要求变量的分布,但秩相关系数与样本的排序有关,而与样本具体的值关联不大,因此,秩相关随机变量的拉丁超立方抽样可通过秩相关矩阵得到。

相关随机变量Z如果满足Z=ξPT,而VS=PPT,VS为变量Z秩相关矩阵,则Z与ξPT具有相同的秩相关系数,其中ξ为一组相互独立的随机变量[14]。

既然秩相关系数与相关随机变量具体的分布没有关系,那么可以设ξ为标准正态分布,即Z为正态分布。

假设一组包含m个秩相关的相关随机变量X=(x1,x2,…,xm)需抽取N个样本,秩相关矩阵为VS,通过Python语言实现拉丁超立方抽样过程如下:

Step 1通过拉丁超立方抽样对随机变量ξ进行抽样,ξ=(ξ1,ξ2,…,ξm),其中:ξ1、ξ2、…、ξm为相互独立的标准正态分布随机变量,每个变量共抽取N个样本。

Step 2对VS进行Choleshy分解得到PT,通过Z=ξPT转换得到正态分布Z的N个样本,分别对Z=(z1,z2,…,zm)中每个变量的N个样本进行排序,得到排序序号。

Step 3通过拉丁超立方抽样分别对xi(i=1,2,…,m)抽取N个样本,并对这N个样本进行排序,排序序号与第i个变量zi的N个样本排序号相同,从而得到秩相关随机变量X=(x1,x2,…,xm)的N个拉丁超立方抽样样本。

以岩土工程中土体常见的参数c、φ为例进行拉丁超立方抽样,抽取10 000个样本。两个参数的均值u分别为uc=10 kPa、uφ=30°,标准差Δc=2 kPa、Δφ=2°,其中c满足对数正态分布、φ满足正态分布,Spearman秩相关系数为-0.5。抽样结果如图4。

图4 Spearman秩相关抽样结果

2 隧道掌子面失效概率分析

2.1 实例背景

目前,隧道工程仍以确定性分析为主,但其围岩的材料参数往往具有不确定性,因此,有必要对某些情况进行不确定性分析或可靠度设计[17]。不确定性分析方法可以是蒙特卡洛抽样和数值计算方法的结合[18]。为了展示拉丁超立方抽样在工程应用中的优越性,笔者用一个直径D=6 m,埋深H=6 m的圆柱形隧道掌子面进行失效概率分析。隧道周围土体采用摩尔-库伦模型,衬砌采用弹性模型。将土体的黏聚力c和内摩擦角φ考虑为服从正态分布的随机变量,两个参数的均值u分别为uc=10 kPa、uφ=30°,标准差Δc=2 kPa、Δφ=2°,Pearson相关系数为-0.5。土体的重度γ=18 kN/m3,弹性模量E=240 MPa,泊松比ν=0.3。隧道采用全断面开挖,不考虑超前支护措施。

2.2 三维数值模型

图5为概率分析所用的三维数值模型,考虑隧道结构和荷载的对称性,仅建立了1/2模型进行分析。为避免边界效应的影响,根据圣维南原理,隧道开挖边界距模型边界应为3～5倍洞径D,因此分析时,隧道开挖边界至模型的水平边界以及模型底部边界的距离均取3D,掌子面距模型纵向边界的距离也为3D。在模型的纵向上,掌子面前方一倍洞径的土体网格单元为0.5 m,其它部分的网格纵向尺寸为2 m;模型单元为57 400个,节点为62 118个;边界条件上,模型的左右和前后边界为法向约束,模型的底部为全约束。

2.3 模拟过程

要计算图5数值模型的隧道掌子面的失效概率,需抽取一定数量的样本进行确定性分析。为保证一定的精度,样本的数量N应满足

N≥100/Pf

(10)

式中:Pf为失效概率。

笔者采用批量采样的方式,进行确定性分析,统计失效样本的数量,每批次采集1 000个样本;重复这一步骤,直到满足NPf≥100,终止采样,计算最终的失效概率。

对采集的每个样本(ci,φi),传统方法是通过FLAC3D自带的强度折减法来计算安全系数f的。f≥1,表示隧道掌子面稳定;f<1,表示隧道掌子面不稳定。

为提高计算效率,笔者不计算安全系数具体值,而是通过运行命令“solve fos bracket 1.0 1.0”得到计算的最大不平衡力比值r。当r<1×10-5时,表明迭代计算是收敛的,即在不进行折减的情况下,隧道掌子面是稳定的;当r≥1×10-5时,掌子面不稳定。

图6为数值模型在某一黏聚力c与内摩擦角φ组合下的计算结果。可见,模型基本没有塑性区,r=9.96 × 10-6,因此,掌子面是稳定的。

图6 三维数值模型计算结果

2.4 结果分析

图7为用蒙特卡洛法计算得到的隧道掌子面失效概率分析结果。

图7 样本数量与失效概率

由图7可见,当样本数量N=97 000个时,掌子面失效样本的数量为100个,此时的失效概率Pf=100/97 000≈0.001。在蒙特卡洛模拟中,95%置信区间允许的误差为[19]:

(11)

即,满足95%置信区间的失效概率范围为:[0.8Pf, 1.2Pf]=[0.000 82, 0.001 24]。

根据拉丁超立方抽样采样结果,当样本数量达到16 000次时,已能满足所需的计算精度。所需样本数量仅为蒙特卡洛抽样样本数的16.5%。由此可见,拉丁超立方抽样更具代表性,可以显著降低概率分析所用的样本数量。

3 结论

拉丁超立方抽样从多元分布中独立抽取最具代表性的样本,在保证计算精度的同时,可大大减少抽样样本数,但拉丁超立方抽样不适用于相关随机变量的直接抽样,需进行一定的转换。笔者通过Python编程将4种不同类型的相关随机变量转换为独立标准正态分布随机变量进行拉丁超立方抽样。具体为:正态分布与对数正态分布用协方差矩阵通过Choleshy分解实现相关随机变量的转换;非正态分布通过Nataf变换实现相关随机变量的转换;秩相关通过秩相关矩阵分解实现相关随机变量的转换。同时,基于独立标准正态分布相关随机变量拉丁超立方抽样,开展了隧道掌子面稳定性概率分析,并与蒙特卡洛模拟结果进行了对比。研究得到以下主要结论:

1)相关随机变量拉丁超立方抽样的抽样结果与其理论分布结果基本吻合,验证了拉丁超立方抽样方法的准确性。

2)隧道掌子面稳定性概率分析表明,拉丁超立方抽样所需样本数为蒙特卡洛抽样样本数的16.5%即可满足计算精度要求,极大地提高了计算效率。