基于神经网络算法的沥青路面使用性能 组合预测模型研究

曹雪娟,卢治琳,吴博文,黄 莹,王 民

(1. 重庆交通大学 材料科学与工程学院,重庆 400074; 2. 重庆交通大学 土木工程学院,重庆 400074; 3. 重庆市智翔铺道技术工程有限公司,重庆 400067)

0 引 言

目前,我国高速公路已经从最初的大规模建设阶段逐步过渡到沥青路面的养护和管理阶段。科学合理地评价沥青路面使用性能是制定养护计划的基础[1-3],因此,对沥青路面使用性能进行准确预测至关重要。

国内外常用的沥青路面使用性能预测模型主要分为概率型和确定型两类。随着计算机技术的发展,灰色预测模型、神经网络预测模型和组合预测模型逐渐成为研究焦点[4-6]。灰色预测模型可以通过较少的建模数据得到较高的预测精度,但对随机因素变化较大的沥青路面预测效果较差[7-9]。神经网络预测模型具有较强的信息处理和自学习能力,已成功应用于道路工程领域[10-11],径向基(radial basis function,RBF)因其可以逼近任意的非线性函数被广泛应用,但存在容易陷入局部最优值的问题[12-13]。目前研究多采用组合方法对目标进行预测,如主成分分析法(principal component analysis,PCA)和遗传算法(genetic algorithm,GA)等,组合预测模型优于单一数学模型分析的定性研究,预测结果与实际状况更加吻合[14-17]。

笔者提出了一种基于RBF的沥青路面使用性能组合预测模型——PCA-GA-RBF。将模型训练阶段的计算误差作为目标函数,引入PCA对路面使用性能影响因素进行降维处理;利用GA优化RBF结构,为沥青路面使用性能预测提供了可靠的依据。研究表明:组合预测模型PCA-GA-RBF结构简单、收敛速度快、预测精度高。

1 模型建立

首先定义一个非线性映射,将沥青路面使用性能影响数据集(路龄、年均气温、年均降雨量等)映射到高维特征空间中,然后在此特征空间中对路面使用性能进行线性回归,最终达到预测路面使用性能的目的。步骤如下:

1)收集原始数据并进行预处理;

2)运用主成分分析法对建模数据进行降维处理,将计算结果作为模型的输入变量;

3)运用遗传算法进行全局寻优计算,确定最优模型参数λ、α;

4)以路面行驶质量指数(IRQ)为模型输出变量,建立神经网络训练模型;

5)对组合预测模型PCA-GA-RBF进行评估。

基于组合预测模型PCA-GA-RBF的沥青路面使用性能算法流程如图1。

图1 组合预测模型PCA-GA-RBF算法流程

1.1 数据预处理

为了提高组合预测模型PCA-GA-RBF样本数据的质量,减少异常数据和缺失数据对回归性能的干扰,同时加快RBF模型的训练速度,笔者对原始数据集做了如下预处理。

1.1.1 数据组成分析与优化

笔者收集整理了四川省2014—2019年23条高速公路的路面施工建造、环境气候、交通量和路面养护等4大模块数据,基于沥青路面使用性能指标体系,挖掘出15个对沥青路面破损状况有较大影响的因素,详见表1。将整理的沥青路面使用性能数据信息导入SQL Server平台,建立数据库,“上面层材料类型”“中面层材料类型”等材料类型数据在软件中量化为0、1、……形式。

表1 沥青路面使用性能影响因素

1.1.2 剔除异常数据

根据JTG 5210—2018《公路技术状况评定标准》,路面性能指标检测得分在0～100之间,数值越大表明路面性能越好,超过上限100或低于下限0的数据可以明确划分为异常值剔除。

1.1.3 缺失数据分析

缺失数据主要包括记录的缺失和记录中某个字段的缺失,笔者采用多重插补法(MI)对缺失数据进行处理,从包含缺失值的数据集中生成多组完整的数据集。

1.2 沥青路面使用性能影响因素主成分分析

1.2.1 主成分分析法

在不减少原始数据所包含信息的前提下,为了能够对原始数据进行降维处理,以使计算方差最优,笔者采用主成分分析法来选取影响沥青路面使用性能的主成分因素。路龄、年均气温、年均降雨量等15个路面使用性能影响因素即为主成分分析中的主成分因素,基于Karhunen-Loeve变换原理求解特征方程,采用MATLAB提供的主成分分析函数princomp进行主成分分析,最终得到15个因素的主成分分析碎石图(图2),图中仅展示了前10个主成分因素。

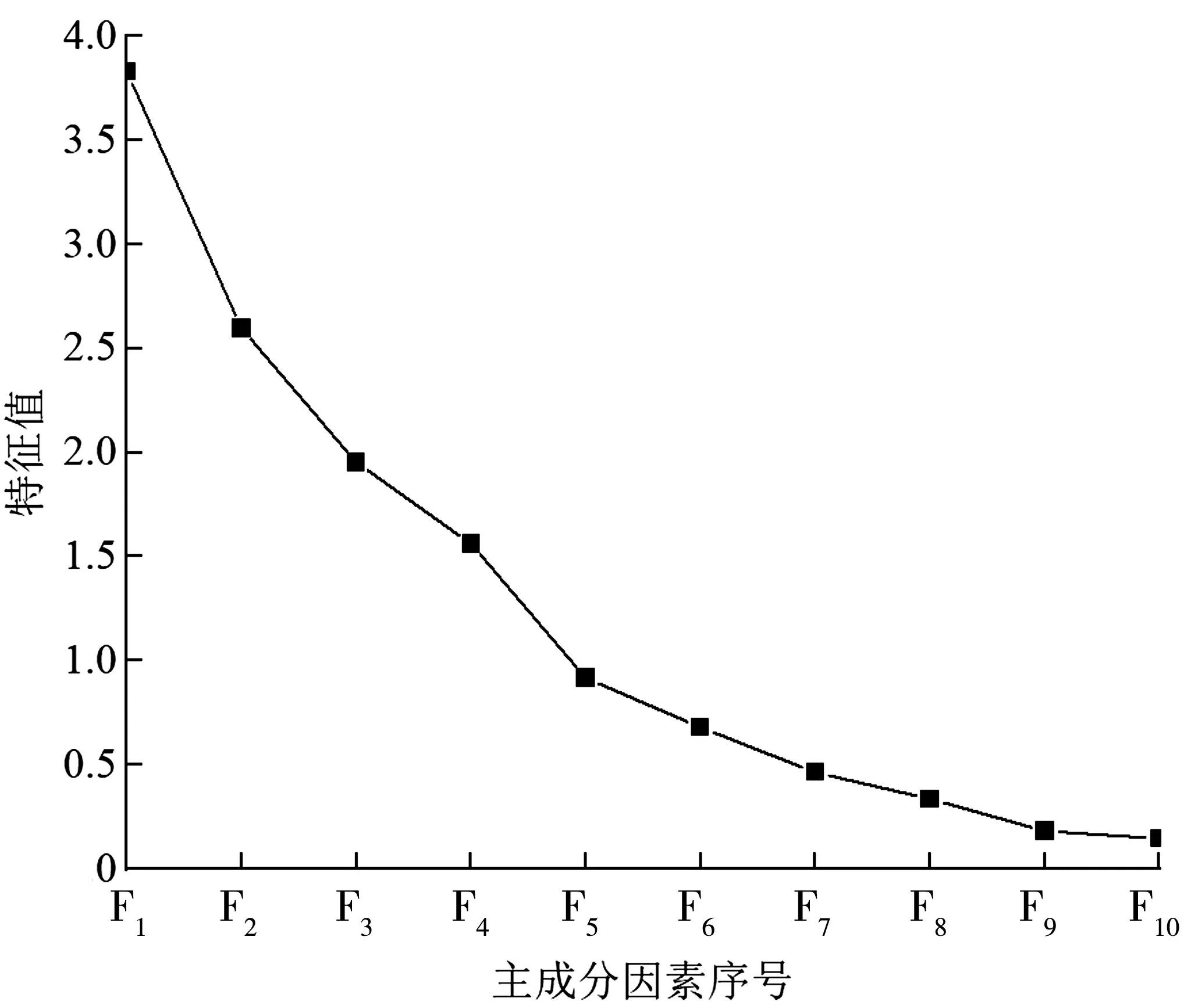
图2 主成分分析

由图2可见,F8主成分因素之后曲线斜率变化趋于平稳,并且F9与F10主成分因素之间的线段斜率近乎为0,说明F9、F10主成分因素所包含的原始数据信息非常少,分析时可不考虑。因此,笔者选取前8个主成分因素进行分析。

1.2.2 主成分分析法可靠性验证

表2为主成分特征值的贡献率比较结果。

表2 主成分特征值的贡献率

由表2可知,8个主成分因素的综合献率超过85%,因此,选取这8个主成分因素进行分析较为合理,既保留了足够多的原始信息,又实现了降维处理。

1.3 模型参数优化

RBF的计算效率与性能由参数λ、α决定,笔者将遗传算法的计算结果作为初始权值进行模型优化。

1.3.1 染色体编码

为了提高参数寻优精确性,采用二进制编码方式,避免后续选择、交叉和变异过程中的编码与解码,最终构建的RBF的拓扑解构为8-48-1,从而,确定RBF中间隐藏层的神经元个数为48。

1.3.2 适应度函数的选择

适应度函数决定了模型的寻优方向。针对RBF参数优化问题,笔者选取均方差误差函数M作为适应度函数,如式(1):

(1)

1.3.3 选择、交叉和变异

采用轮盘赌的方式选择新的种群,染色体被选择的概率随函数值的增大而增高,交叉和变异均依照系统设置概率进行操作。经过RBF的反复迭代,最终寻找出基于全体样本的最优参数λ=0.58、α=0.997。遗传算法优化过程的相关参数设置如表3。

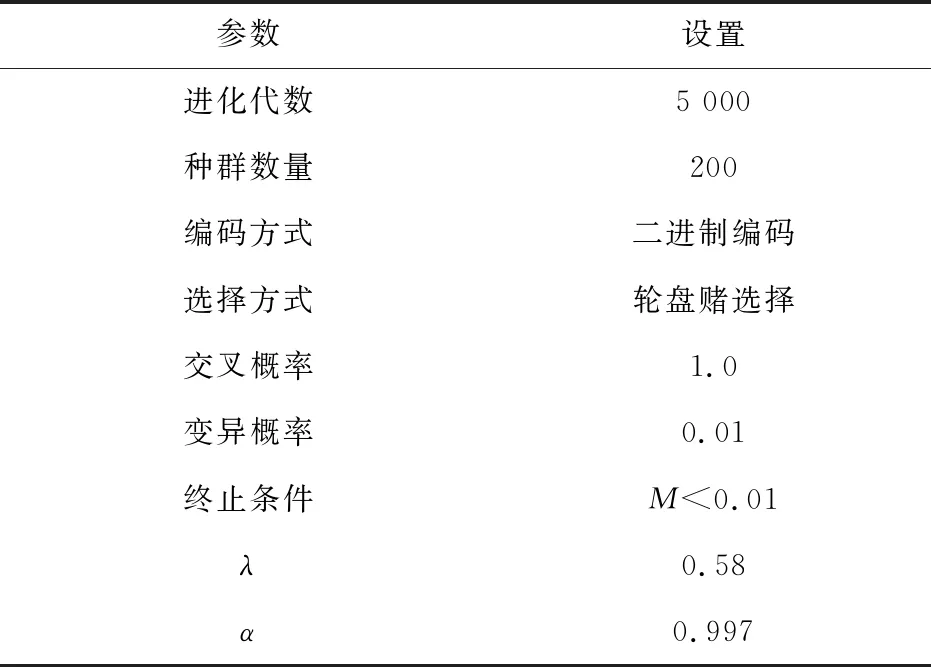
表3 遗传算法优化参数

1.4 PCA-GA-RBF组合预测模型建立

1.4.1 确定输入变量和输出变量

将主成分分析所得的8个主成分因素作为组合预测模型的输入变量,沥青路面行驶质量指数(IRQ)作为预测模型的输出变量,共同构成数据总量为5 000组的建模数据集。

1.4.2 选定训练样本集与测试样本集

为保证PCA-GA-RBF有较好的预测效果,避免计算过程出现过拟合的现象,将整体建模数据集划分为训练集与测试集2类,训练集数据∶测试集数据为70∶30,即训练集3 500组数据,测试集1 500组数据。

1.4.3 确定径向基函数

采用高斯函数作为径向基函数φ(x),以减少多变量输入的复杂程度。

1.4.4 遗传优化算法对回归参数寻优

为了提高PCA-GA-RBF的预测精度,采用遗传算法对高斯函数的中心向量Ci和宽度σi进行最优参数选择。

由于RBF的输出层根据需求为单个预测值,权值向量为w=[w1,w2,…]T,故预测值表达式为

yi=wφ(x)

(2)

利用R语言编程平台,建立组合预测模型PCA-GA-RBF。

1.5 组合预测模型PCA-GA-RBF评估

1.5.1 PCA-GA-RBF与RBF对比

PCA-GA-RBF、RBF训练模型的训练过程如图3。

图3 PCA-GA-RBF、RBF训练过程

由图3可见,与RBF相比,PCA-GA-RBF训练过程曲线斜率较大,迭代次数较少,计算速率更快。表明主成分分析可减少迭代次数,实现对数据的降维处理,简化了模型结构。

1.5.2 PCA-GA-RBF预测精度检验

图4为PCA-GA-RBF与RBF模型的预测结果。

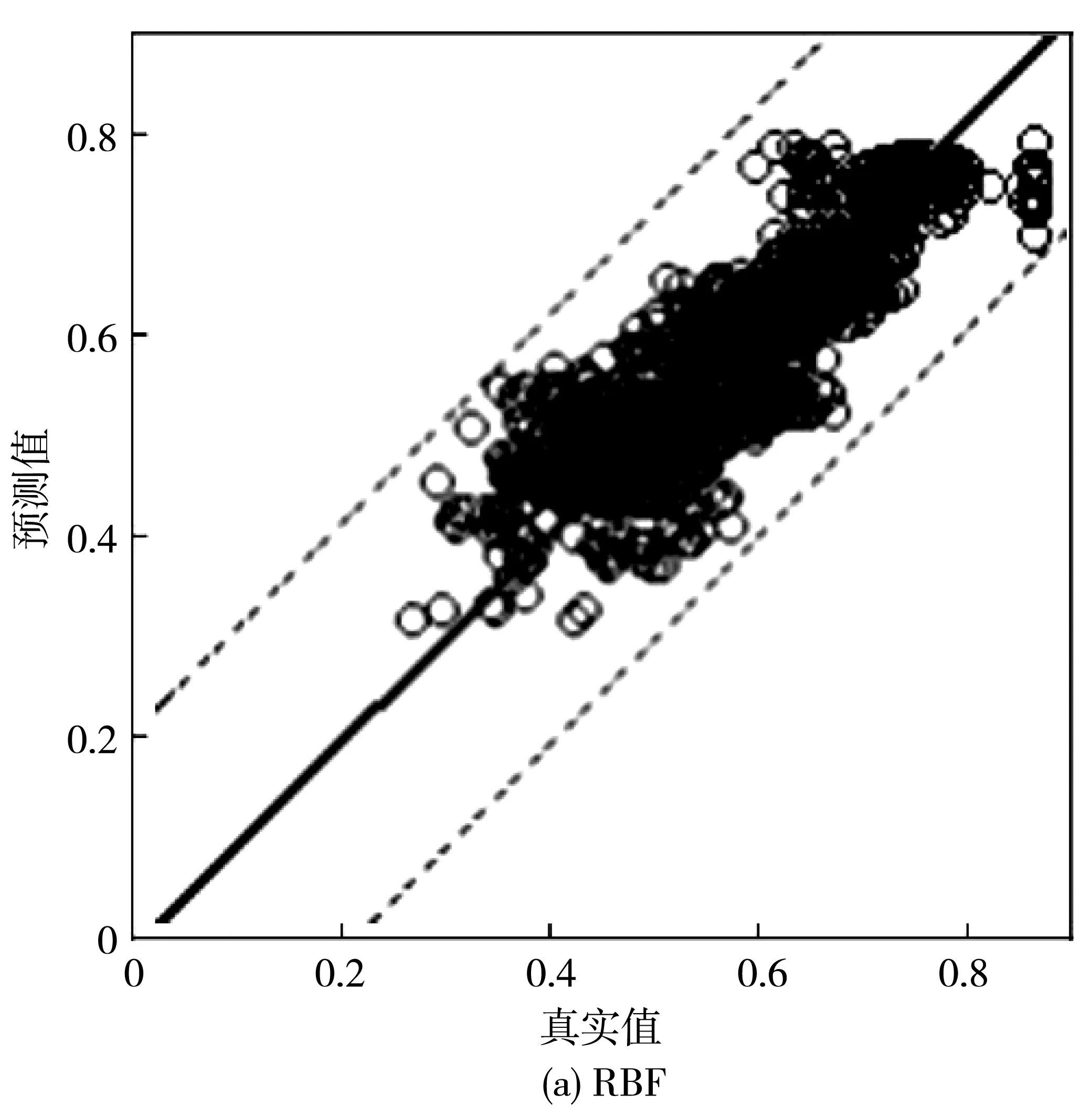
图4 PCA-GA-RBF、RBF预测结果

从图4可以看出,图4(b)中各个离散点的分布较密集,即离散程度较小,说明PCA-GA-RBF的预测精度较高,真实值与预测值之间的偏差波动较小,结果较可靠。

1.5.3 PCA-GA-RBF有效性与准确性检验

采用与构建组合预测模型PCA-GA-RBF相似的方法,构建PCA-GA-BP模型,其中数据预处理和沥青路面使用性能影响因素也采用主成分分析法。经过试算验证后,确定了PCA-GA-BP模型的最优网络结构,即第一层神经元个数为6个、第二层神经元个数为5个的网络结构。调用R语言平台neuralnet函数构建BP、PCA-GA-BP训练模型,两者完成计算分别共进行了9 876、7 962次迭代。

表4为BP、PCA-GA-BP和RBF、PCA-GA-RBF预测模型拟合优度R2与均方根误差S的计算结果。可见,4个模型中,组合预测模型PCA-GA-RBF的R2最接近1,S最小,表明其预测结果有效且精度较高。

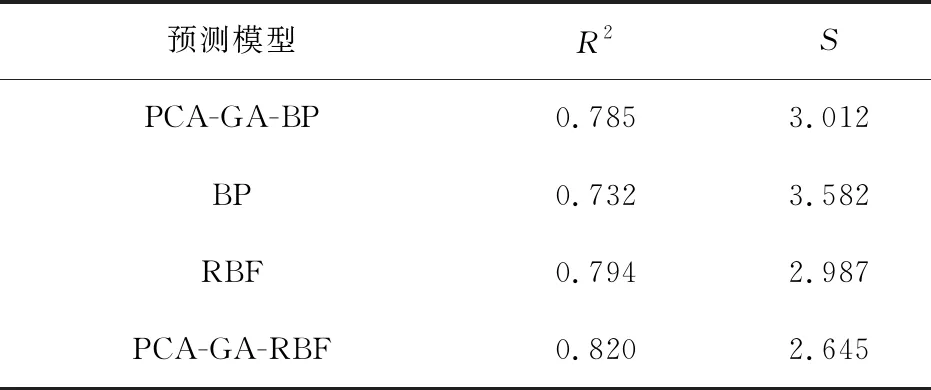
表4 4种神经网络预测模型评估结果

2 实例验证

2.1 数 据

随机选取了四川省2014—2019年10条高速公路共计2 280个IRQ记录数据,将建模数据集按照训练集数据∶测试集数据为70∶30进行划分,即训练集1 596组数据,测试集648组数据。

2.2 评价指标

根据JTG H 20—2007《公路技术状况评定标准》,路面平整度评价标准见表5,路面行驶质量指数IRQ按式(3)计算:

(3)

式中:IIR为国际平整度;a0、a1为标定系数,a0=0.026,a1=0.650。

表5 路面平整度评价标准

2.3 沥青路面使用性能预测

沥青路面使用性能真实值与PCA-GA-RB预测值如图5。可见,预测曲线拟合优度R2=0.850,各离散点分布相对密集,表明组合预测模型的泛化能力较强,误差波动性较小。

图5 PCA-GA-RBF预测结果

2.4 评价结果对比

统计的2 280个IRQ记录数据中,路面平整度实际等级为优、良、中的IRQ数据个数见表6。同时,采用组合预测模型PCA-GA-RBF预测沥青路面的IRQ,再根据表5得出路面平整度预测等级,预测等级分别为为优、良、中的IRQ数据统计见表6。

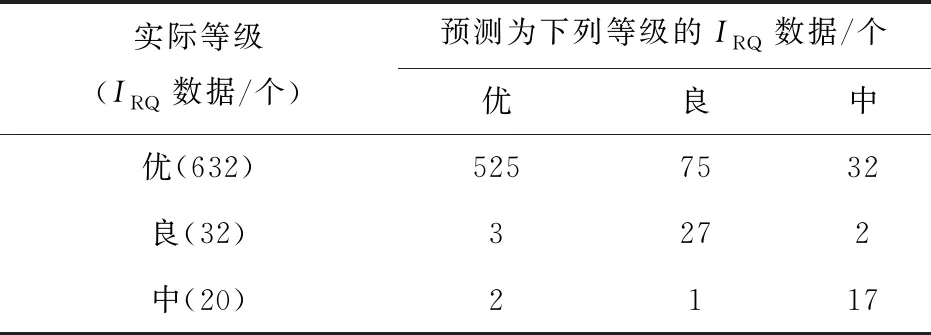
表6 路面平整度实际等级和预测等级的IRQ数据统计

表6中,当路面平整度预测等级和实际等级均分别为优、良、中时,预测所用IRQ数据个数A*分别为525、27、17,路面平整度实际等级分别为优、良、中时,IRQ实际数据个数B*分别为632、32、20,则PCA-GA-RBF对路面平整度实际等级为优、良、中的预测准确率Q=A*/B*,从而可以得到,PCA-GA-RBF对路面平整度实际等级为优、良、中的预测准确率分别为83.1%、84.3%、85.0%,可见预测的准确率较高。

3 结 论

引入PCA和GA以优化RBF模型,得到了沥青路面使用性能组合预测模型PCA-GA-RBF;将PCA-GA-RBF应用于路面行驶质量的预测,并与实际路面行驶质量指标进行对比,验证了PCA-GA-RBF的准确性。研究得到以下主要结论:

1)在BP、PCA-GA-BP及RBF、PCA-GA-RBF等4个模型中,PCA-GA-RBF的拟合优度R2最接近1,均方根误差S最小,表明PCA-GA-RBF预测精度最高。

2)PCA-GA-RBF组合预测模型具有泛化力,可以选取单个评价指标进行评价。