基于WOA-XGBoost的空闲停车位短期预测方法

宋 瑞,程子龙,赵日鑫

(北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室,北京100044)

0 引 言

随着国内物质水平的不断提升,各个城市均呈现出机动车保有量持续增长的趋势,随之暴露出的便是城市“停车难”问题。由于国内各个城市智慧停车场建设尚未完善,驾驶者在停车过程中表现出获取信息不对称等问题,以致于造成大量机动车在城市道路中“巡游”,造成城市道路拥堵的同时导致大量尾气排放,污染城市环境。对于一些大型停车场来说,停车位信息是不断变化的,仅仅提供停车位的实时信息,会忽略驾驶者在行驶过程中停车位数量的变化情况,不能保证驾驶员到达停车场时可以找到空闲停车位,很容易造成驾驶员“跑空”的尴尬情形,导致大量无效交通的产生。尤其是驾驶员在行驶过程中遇到中心城区拥堵现象的发生,则会进一步加剧获取信息的不对称性。实现停车场空闲停车位的短期预测,为驾驶者提供全面的停车位信息可以缓解驾驶者获取信息不对称问题,进一步提高停车诱导成功率,改善城市停车难问题。

由于受到停车场类型、天气、道路交通情况、驾驶员行为以及采集过程中的干扰等多种因素影响,停车位数据构成的时间序列会表现出较高的复杂性和随机性。对此,国内外学者针对停车位短期预测提出了多种预测模型,笔者将其主要分为两种。一种是以模型驱动为主的预测模型[1-3],主要是针对停车过程建立基本模型并通过标定参数进行空闲停车位的短期预测。另一种是以数据驱动为主的预测模型,包括基于数理统计和机器学习的方法建立模型进行预测,如JI Yanjie等[4]采用三层小波神经网络对停车场内短期停车位可用率进行预测;肖雪[5]通过聚类分析停车数据获取车辆到达和离开的规律,采用马尔可夫生死过程建立模型进行预测,同时利用粒子群优化LSTM(long short-term memory)对停车需求进行了预测;章伟[6]提出了傅里叶变换-最小二乘支持向量回归的多步预测方法,进一步提高了预测精度;A.KLAPPENECKER等[7]通过连续时间的马尔科夫链进行建模对停车位进行预测,这种方法简单快捷,但是鲁棒性较差,预测结果有时存在较大误差。这些模型中神经网络模型具有较强的容错性,但训练速度有待提高。

目前集成算法在各类数据科学竞赛以及不同领域预测方面得到广泛应用。相比传统的神经网络,集成算法拥有更快的训练速度,预测准确率也有较大的提升。其中,XGBoost(extreme gradient boosting)是一种基于Boosting集成思想的集成算法,具有高效、灵活、便捷的特点。XGBoost将决策树作为弱学习器,并通过集成多个弱学习器从而获得更好的预测结果,具有速度快、表现好的优越性。付宇等[8]对北京轨道AFC数据进行处理并采用XGBoost预测模型对轨道交通站点进出客流量进行预测;陈剑强等[9]采用XGBoost模型实现电网负荷短期预测,并通过对比证明了所提模型具有更高的准确性。通过总结发现,相比单一预测模型,通过智能优化算法实现超参数寻优的组合预测模型具有更高的预测精度。其中,鲸鱼优化算法是一种新型启发式算法,具有收敛速度快,全局寻优等特点。对此,笔者首先对空闲停车位数据进行预处理,然后引入XGBoost算法并结合鲸鱼优化算法实现初始参数的寻优,构建组合预测模型,最后通过实例验证所提模型的有效性。

1 数据分析及预处理

文中所用数据为英国伯明翰城市停车场数据,该数据集采集时间为2016年11月1日—2016年11月30日,如图1。首先需要对停车场空闲停车位数量变化的随机性进行分析以及预处理操作。总体而言,该数据集整体变化趋势大致相同。

图1 2016年11月1日—11月7日空闲停车位数据

1.1 随机性分析

停车场空闲停车位数据在采集过程中会受到多种随机因素的干扰,造成数据的剧烈变化。对此笔者采用波动率来更好地描述空闲停车位数据的随机性,如图2。假设时间序列为XN,则某一时间点数据的波动率vk=[(Xk+1-Xk)/Xk],k=1,2,…,N-1,其中N为数据总长度,k为对应的序号。

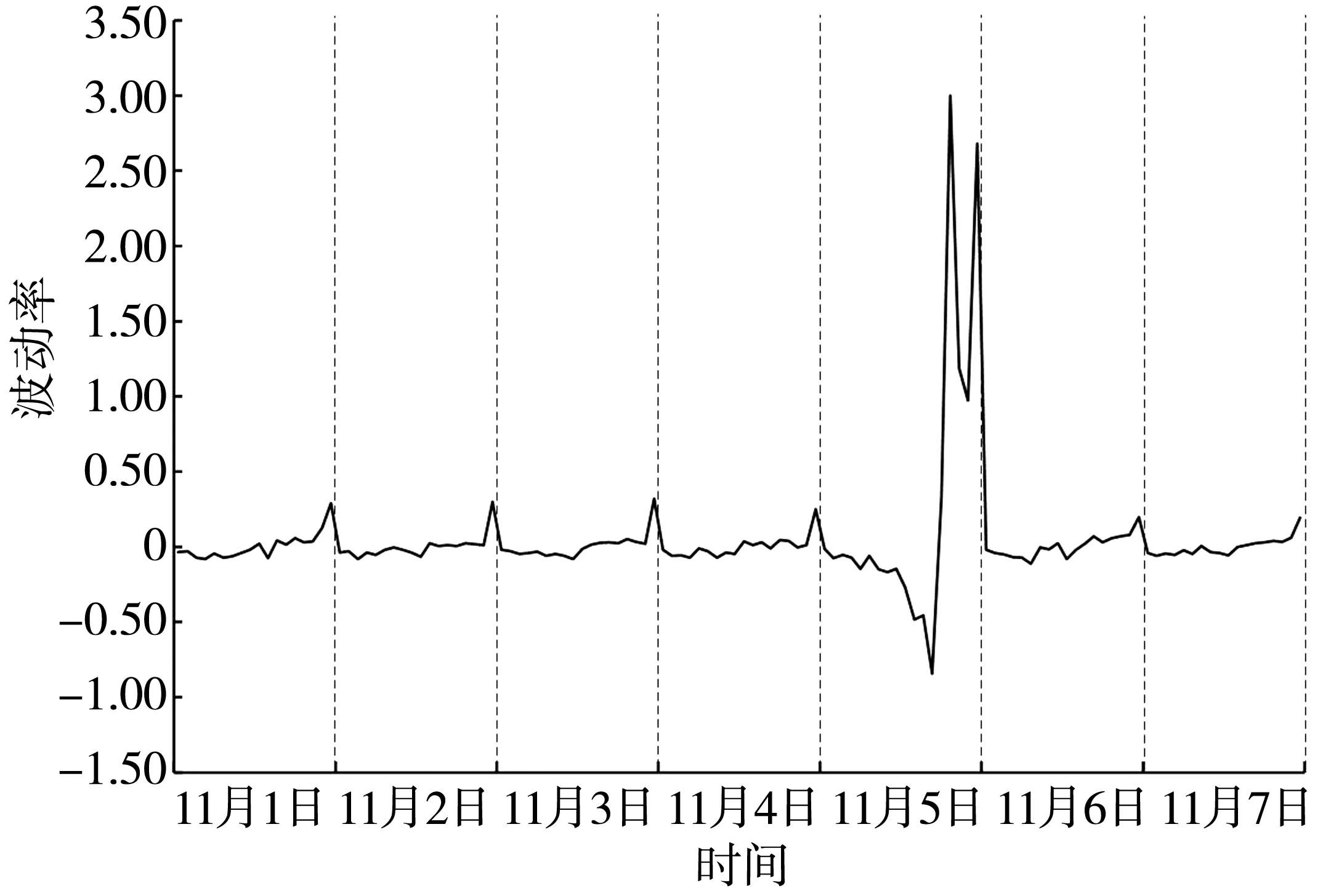
图2 空闲停车位数量序列波动率

1.2 奇异谱分析

由图2可知,该数据具有很强的波动性且波动规律性较弱,存在较大的噪声干扰。对比小波分析,奇异谱分析可以更好地的提取数据的有用信息剔除噪声数据[10]。笔者将采用奇异谱分析实现对数据的预处理。奇异谱分析结合了线性代数、多元统计、动力系统、信号处理等传统时间序列分析方法。在对非线性时间序列进行处理时,奇异谱分析根据原始时间序列构造轨迹矩阵,并对轨迹矩阵进行分解和重构,从而实现对原始时间序列不同成分的提取以及噪声的剔除。

首先,对原始时间序列进行轨迹矩阵的构造,选择合适的窗口长度M,采用滑动窗口的方式进行等间隔采样,将原始时间序列进行滞后排列,从而得到原始时间序列的轨迹矩阵。假设原始时间序列为X={X1,X2,…,XN},其中N为原始时间序列长度。M为给定窗口长度,取值范围为1≤M≤N/2。由此可得出L=N-M+1,则轨迹矩阵Y为M×L的矩阵:

(1)

其次,对轨迹矩阵Y进行奇异值分解和分组。最后通过对角平均化可以将分组得到的矩阵转化为一系列长度为N的新序列,可根据贡献率选择贡献大的成分序列进行重构从而达到原始序列降噪的目的。笔者采用后验的方法,设置窗口长度为256,提取前14个主成分,对停车场数据进行重构,重构序列如图3。

图3 停车场数据SSA处理结果

2 预测模型的提出

2.1 鲸鱼优化算法

鲸鱼优化算法(whale optimization algorithm,WOA)是由S.MIRJALILI等[11]于2016年提出的一种启发式优化算法,通过模拟座头鲸狩猎行为找寻问题最优解,具有调整参数少、全局搜索能力强、操作简单的特点。笔者将其应用于XGBoost超参数的寻优。鲸鱼优化通过随机选择的鲸鱼位置来更新其他鲸鱼的位置,避免陷入局部最优,从而实现全局最优搜索。x(t)为鲸鱼当前位置;t为当前迭代次数,通过系数A实现全局寻优,其数学模型如式(2):

(2)

式中:xrand为群体中随机选择的鲸鱼位置;A和c为系数;r1,r2为[0,1]中的随机数;Tmax为最大迭代次数。

在包围猎物过程中,WOA算法将会假定当前的最佳候选解是目标猎物或接近最优解,然后其他鲸鱼个体会朝着最优位置更新位置,数学模型如式(3):

(3)

式中:x*(t)表示当前最优解。

同时座头鲸在狩猎过程中会在一个缩小的圆圈内绕着猎物游动,同时螺旋式靠近猎物。为了更好地表达这一行为,通过设置概率系数p,当p≥0.5时,采用螺旋式更新位置,反之采用包围式更新位置,数学模型如式(4)、式(5):

(4)

(5)

式中:b=1;l∈[-1,1];pi取值为0.5。

2.2 XGBoost算法

XGBoost算法是一种基于Boosting集成思想的算法,使用了一阶偏导和二阶偏导。二阶导数的应用有利于梯度下降得更快更准。同时为了防止模型过拟合,XGBoost在目标函数中加入了正则项,用于控制模型的复杂度。其目标函数定义如式(6)、式(7):

(6)

(7)

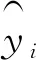
最后通过泰勒展开公式获得最终目标函数如式(8):

(8)

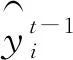
2.3 WOA-XGBoost模型预测流程

笔者将通过鲸鱼优化算法实现对XGBoost模型中树的深度、学习率、子模型数量进行参数寻优,进一步提高模型精度。其中适应度函数采用模型训练的均方根误差进行计算。首先,确定XGBoost模型拓扑结构,确定寻优参数。其次,初始化种群,计算每个个体的适应度值,不断进行位置更新。最终,记录最优个体适应度值以及位置并将其传输至XGBoost模型,对模型进行训练获得最终预测模型。具体流程如图4。

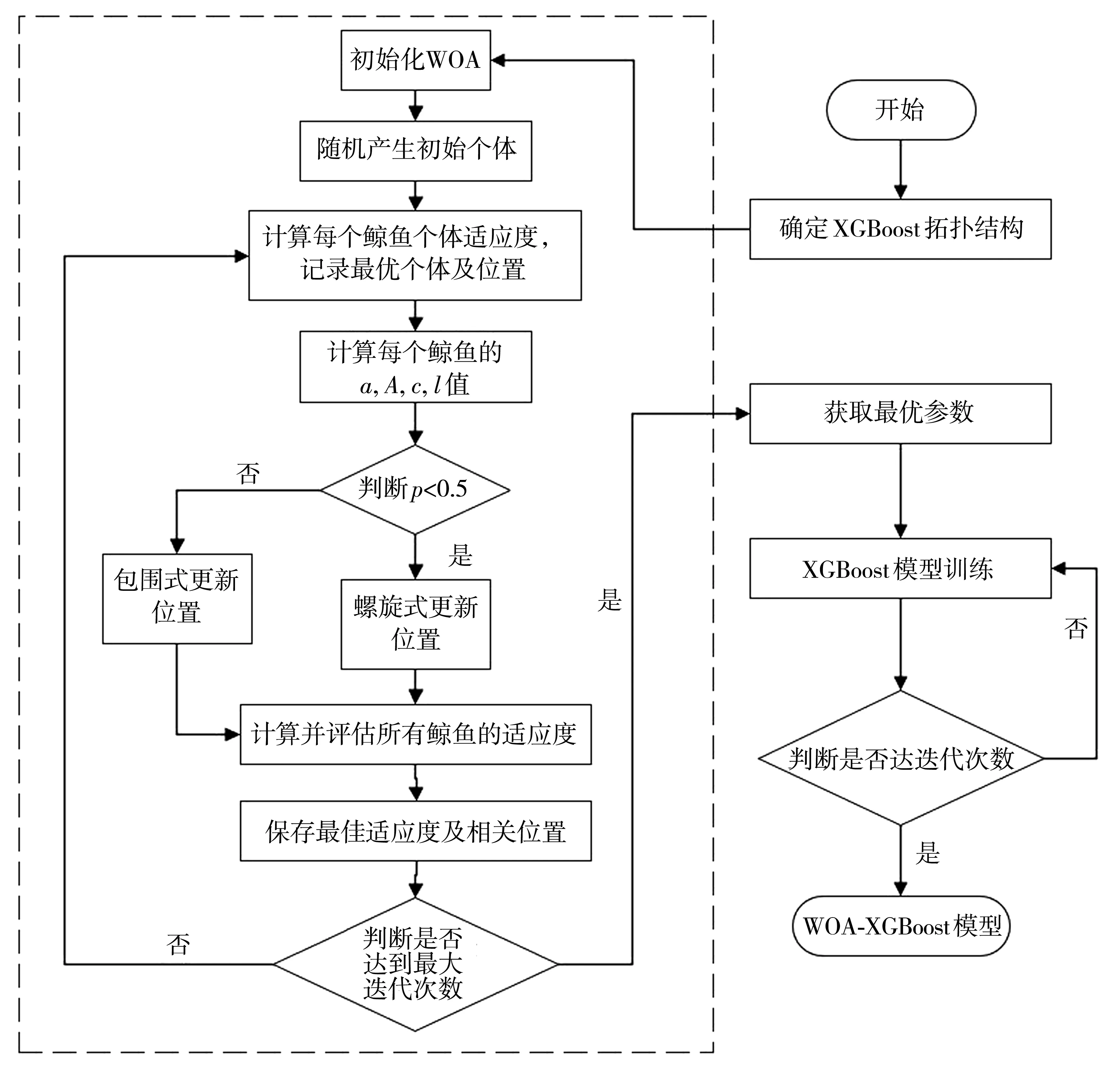
图4 WOA-XGBoost流程

3 实例验证

3.1 数据来源及参数设置

选取英国伯明翰城市停车场数据2016年11月1日—11月29日的数据作为训练集,11月30日数据作为测试集,采用均方根误差等作为评价指标,用来验证模型的有效性。

鲸鱼优化算法具有参数少、易操作的特点,对此笔者设置参数b为默认值1,种群数量为30,迭代次数为50。由于只针对XGBoost模型的学习率、树的最大深度、生成的最大树数目进行寻优,故设置鲸鱼优化算法维度为3。设置XGBoost模型初始树的最大深度为5,学习率为0.05,生成最大树的数目为100,测试集预测结果的ERMS=7.753,在此基础上可通过优化算法求得最优超参数,进一步提高预测精度。在实现对XGBoost模型参数寻优的过程中需对参数的范围进行界定,设置参数范围:max_depth∈[3,50],learing_rate∈[50,200],n_estimators∈[0.01,0.30]。

图5反映了随着迭代次数的增加鲸鱼优化算法适应度值的变化情况。从图5可以看出,鲸鱼优化算法在一开始便找到了相对较好的参数组合,相较于默认参数情况下均方根误差为7.753,初始均方根误差为5.094,效果较明显。同时算法具有较快的收敛速度,在第20次迭代后,算法收敛,并找到最优参数组合为[7,0.279,140],均方根误差为4.310。

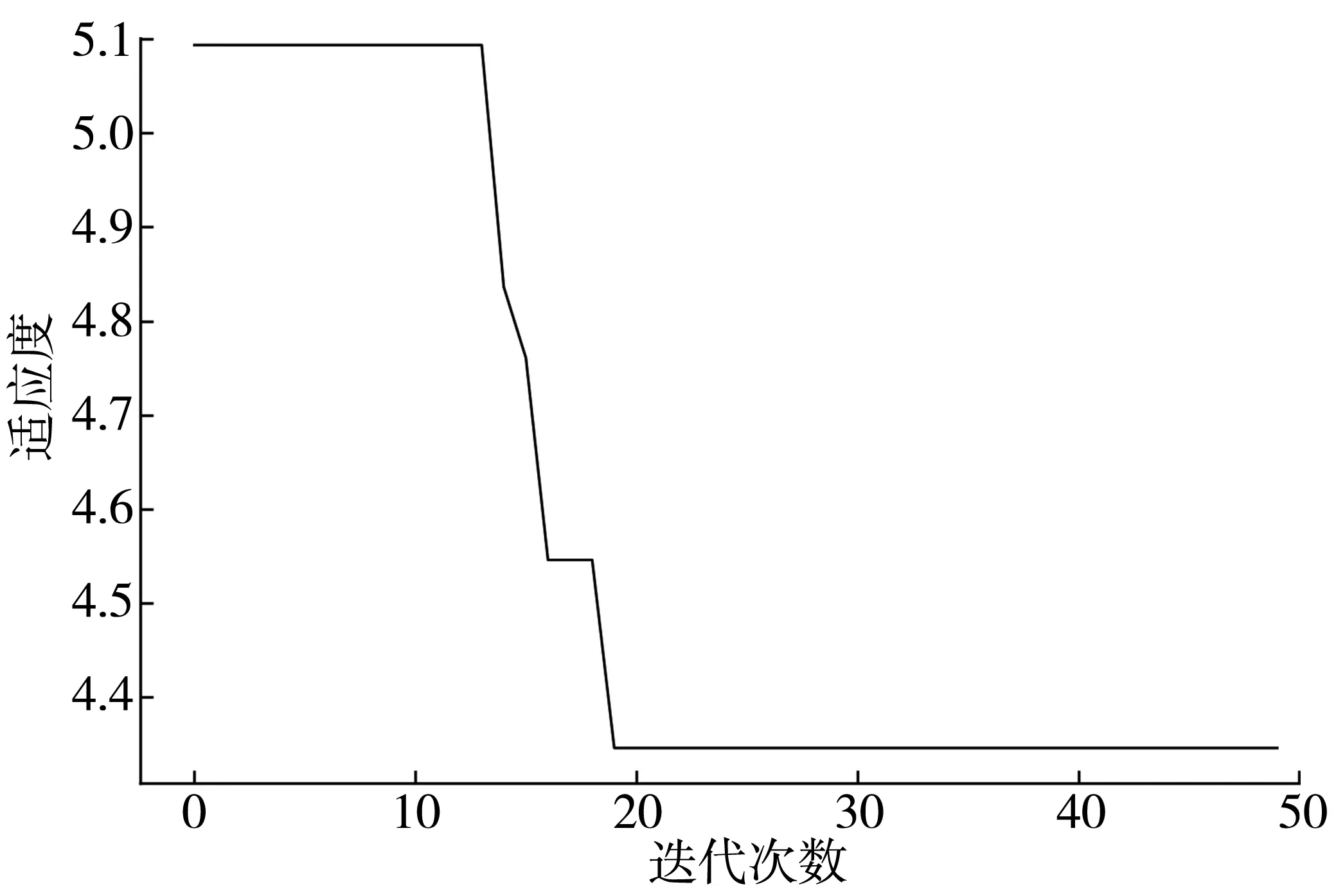
图5 适应度曲线

3.2 预测结果对比分析

为了验证提出模型的有效性,笔者将提出的WOA-XGBoost与默认参数情况下的XGBoost模型以及WOA-SVR模型预测结果进行对比分析。其中RBF核函数具有较高的预测准确率,泛化能力较好[12],故SVR模型采用RBF核函数。评价指标采用平均绝对误差EMA、均方根误差ERMS、回归模型决定系数R2,如式(9)—式(11)。

(9)

(10)

(11)

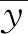
用上述模型分别对测试集进行预测,得到结果如表1和表2,同时将各模型预测值与原始值进行对比,绘制曲线如图6。

通过表1和表2可知,3种预测模型均表现良好,具有较好的拟合度,其中笔者提出的WOA-XGBoost预测方法具有较高的精度,平均绝对误差为3.164辆、均方根误差为4.310辆、R2=0.986。此外,相比其他预测模型,WOA-XGBoost模型预测值拟合度较好,相对误差最大值为3.226%,最小值为0.352%。通过对比WOA-XGBoost模型与XGBoost模型预测结果可知,利用鲸鱼优化算法有利于找到全局最优的参数组合,从而在一定程度上降低了预测误差。通过对比XGBoost模型与WOA-SVR预测结果可知,基于Boosting集成思想的XGBoost模型在停车场空闲停车位短期预测方面的可应用性丰富了停车位短期预测模型体系。同时对比3组预测结果,验证了WOA-XGBoost模型在停车场空闲停车位短期预测方面具有较好的预测结果,稳定性较好,进一步提高了预测的可靠性。

表1 不同预测模型评价指标对比

图6 预测值对比

表2 空闲停车位部分预测值和真实值对比

4 结 论

1)停车场空闲停车位数据在采集过程中可能会受到多种因素的影响,致使数据集具有很强的波动性。奇异谱分析可以更好地提取数据的有用信息,通过奇异谱分析对数据进行预处理,进一步提高数据集的可靠性。

2)将集成算法引入到停车场空闲停车位短期预测当中,在此基础上采用鲸鱼优化算法实现对XGBoost预测模型参数的优化,进一步降低人工设置参数的随机性以及提高整体预测精度。

3)通过与其他预测模型进行对比,证明了笔者提出的组合预测模型具有较好的预测结果以及可靠性。

综上所述,笔者提出的WOA-XGBoost组合预测模型在停车场空闲停车位短期预测方面具有较好的预测结果,可以为驾驶者提供全面的停车位信息,进一步提高诱导成功率,解决城市停车难问题。在未来研究中可以考虑不同停车影响因素对预测结果造成的影响,同时引进精英策略等对鲸鱼优化算法进行改进以提升搜索能力,提高组合预测模型的预测精度。