基于易损性曲线的斜拉桥横向抗震性能评估

2023-05-09徐略勤贺洪滔徐意宏

重庆交通大学学报(自然科学版) 2023年3期

徐略勤,贺洪滔,张超,徐意宏

(1. 重庆交通大学土木工程学院,重庆 400074; 2. 重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074)

0 引言

经过几十年的发展,斜拉桥的设计和施工技术得到了长足的进步,已成为跨越江河湖海、深沟巨壑的主要大跨桥型之一。斜拉桥的适用性很强,其结构体系根据建设条件和受力需求可以衍生出丰富的变化[1]。我国地震带分布广泛,是世界上遭受地震灾害最严重的国家之一。在地震区建设的斜拉桥在纵桥向通常采用飘浮体系来避开地震能量集中段,并通过在塔-梁交接处设置减隔震装置控制主梁纵向位移,但在横桥向,斜拉桥抗震措施的施展空间相对受到更多的限制[2,3]。为了控制主梁的摆尾现象,斜拉桥在辅助墩和过渡墩处往往采取横向固定的约束形式。由于斜拉桥的桥面系质量集中,地震惯性力大,辅助墩和过渡墩一般承担了较大的横向地震力,因此使得它们往往成为抗震薄弱环节[4]。提高斜拉桥的横向抗震性能是工程设计的重点,也是学术界的研究热点之一。

国内外对斜拉桥横向抗震性能的研究已有了一定的积累,但研究重点主要集中在各种减隔震装置对斜拉桥抗震性能的提升方面,如各类阻尼器的参数优化、主被动控制系统的减震分析等[2-6]。采用易损性曲线研究斜拉桥的抗震性能近年来逐渐得到重视。例如,PANG Yutao等[7]考虑材料和构件尺寸两方面15种不确定性因素,基于概率地震需求模型(PSDMs)建立了斜拉桥的地震易损性曲线; W. T. BARNAWI 等[8]针对安装了磁流变阻尼器MR的斜拉桥进行易损性分析,以此探讨MR的减震效果;马凯等[9]基于易损性概率曲线讨论了失相干效应、场地效应、行波效应对飘浮体系斜拉桥抗震性能的影响;钟剑等[10]提出两水准设防的斜拉桥易损性分析方法,通过易损性概率分析研究了拉索减震支座对改善斜拉桥抗震性能的有效性;胡思聪等[11]认为,高墩多塔斜拉桥不宜沿用常规桥梁的地震动强度指标进行易损性分析,而应针对不同情况采用基本周期谱加速度或峰值谱位移。这些研究工作从不同角度对斜拉桥的地震易损性进行了有益的探讨,但结合设计地震强度对斜拉桥横向抗震性能的评估研究仍非常欠缺,仅钟剑等[10]少数学者进行了尝试。实际上,采用易损性曲线法来指导工程抗震评估和设计仍有大量工作需要进一步开展,如构件和体系的损伤超越概率阈值与桥梁结构具体抗震性能目标相对应的问题,各类构件损伤状态及其损伤指标的划分和确定问题等。笔者借助于易损性分析手段,针对某新建斜拉桥的横向抗震性能,从关键构件到结构体系两个层面构建易损性曲线,并结合桥址场地两水准设防地震动进行抗震性能评估,旨为背景工程以及同类斜拉桥的抗震设计提供参考。该研究属于结合工程实践的初步探索。

1 分析背景与模型

1.1 桥梁概况

某新建双塔5跨斜拉桥主跨为285 m,两侧边跨处各设有辅助墩(即2# 墩和5# 墩)和过渡墩(即1# 墩和6# 墩),桥梁全长535 m,立面布置如图1。索塔为两分离式独柱钢筋混凝土结构,3# 和4# 塔上均分别设有单向+双向2个球型钢支座。

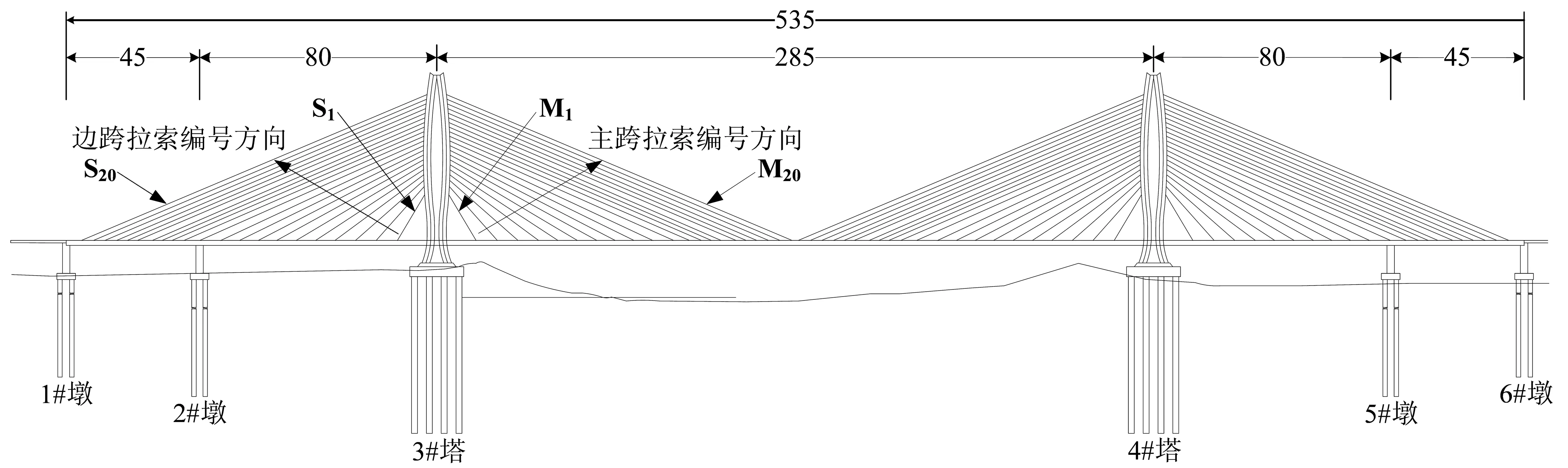
图1 桥梁总体布置(单位:m)

辅助墩和过渡墩均为分离式矩形墩柱,且高度均为11 m,其中前者采用双柱式,后者采用三柱式,如图 2。2# 和5# 墩上均设有单向+双向2个球型钢支座,而1# 和6# 墩上则均设有双向+单向+双向3个球型钢支座。主梁采用预应力混凝土双边箱梁,桥面全宽为44.5 m。斜拉索为双索面布置,共80对。1#～6# 塔或墩均采用群桩基础,其中,塔下桩径为1.8 m,墩下桩径为1.2 m。根据本桥桥址场地地震安全评估报告,两水准地震E1、E2对应的超越概率(100 a)分别为10%和3%,其对应的峰值地面加速度aPG(peak ground acceleration)分别为0.116g和0.177g。

图2 桥梁分析模型(单位:m)

1.2 有限元建模

基于SAP2000分析软件,建立背景工程的三维有限元分析模型,如图 2。全桥的非线性因素主要体现在球型钢支座上,索塔、过渡墩和辅助墩都按弹性梁柱单元建模,但考虑恒载二阶效应。塔和墩的塑性行为和损伤状态主要通过其地震需求与能力之间的相对关系来体现,这么做有一定的误差,但对于实际工程的抗震评估来说是便利的。斜拉索采用桁架单元模拟,考虑垂度效应的弹性模量Ernst修正公式。球型钢支座采用理想双线性滞回模型来模拟。其中,活动方向的摩擦系数取0.03,固定方向的屈服力为支座竖向设计承载力的20%[12];桩-土相互作用采用6×6集中土弹簧模拟,通过m法计算土弹簧的刚度系数。由于边界条件对斜拉桥地震响应的影响不容忽视,尤其在横桥向,因此在主桥模型的左右两端各建立一联引桥模型。在进行时程响应分析时,结构阻尼采用Rayleigh模型,阻尼比根据规范[13]取3%。

1.3 损伤状态和临界指标

准确划分桥梁结构及构件的损伤状态非常困难,尤其考虑到斜拉桥实际震害实例并不多见。因此,笔者结合现行规范[13]的两水准三阶段设防思想,定义了3个损伤临界状态,即:轻微损伤、中等损伤、严重损伤,对应的抗震性能目标大致为维持使用功能、保护财产安全和保障生命安全。结合背景工程的结构特点,选取索塔、斜拉索、支座、过渡墩和辅助墩作为关键评估构件,建立各构件的损伤状态与损伤指标的对应关系。

抗弯、抗剪、延性是描述钢筋混凝土构件抗震能力的基本参考指标。其中,剪切属于脆性破坏模式,可通过配箍构造细节优化来避免。由于笔者采用弹性梁柱单元模拟索塔和墩柱,无法直接得到构件的位移延性需求,因此选取抗弯作为索塔和墩柱的抗震指标,通过P-M-φ分析可得到索塔和墩柱关键截面对应3种状态的抗弯能力,如图3。图3中:以截面纵筋首次屈服对应的弯矩值M0作为轻微损伤临界;通过能量等效原则确定的等效屈服弯矩My作为中等损伤临界;以纵筋拉断或核心混凝土开裂对应的弯矩Mu作为严重损伤临界。

图3 P-M-φ分析曲线

斜拉索是斜拉桥重要的传力构件,损伤状态可采用其在地震与恒载作用下的应变比来α=ε/εd表征[11],α的临界值见表 1。鉴于背景工程在纵、横桥向的结构对称性,笔者仅选取3# 塔的一个索面作为分析对象,该索面在主跨一侧的20根索编号为M1～M20,在边跨一侧的20根索编号为S1～S20,编号的具体对应位置如图1。图4显示了M1～M20和S1～S20在E2地震作用下应变比α的分布规律。由图4可以看到,S1的应变比α最大,最易发生损伤,因此笔者选S1进行斜拉索的地震易损性分析。

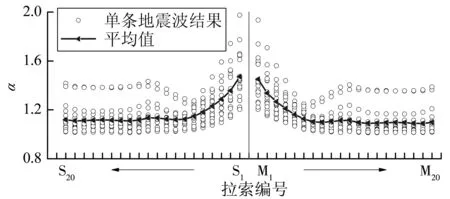
图4 E2地震下拉索应变比α

针对横向固定球钢支座,据M.J. RANDALL等[14]、J.B. MANDER等[15]实验研究成果,横向固定球钢支座横向变形超过 ±40 mm时螺栓将完全断裂,横向固定球钢支座横向变形达到 ±20 mm时其刚度开始恶化,故笔者分别以 ±20 mm、±40 mm为横向固定球钢支座的中等、严重损伤的临界值。针对横向滑动球钢支座,笔者以球型钢支座的横向地震位移大于容许位移 ±40 mm作为其活动方向的中等损伤临界值,以球型钢支座的横向地震位移超过支座中心线 ±150 mm作为其活动方向的严重损伤临界值。

表1列出了背景工程各关键构件的损伤状态及其临界指标值。由于结构对称,仅分析桥梁的左半跨结构,其中,1# 墩、2# 墩和3# 塔以设置固定支座的墩柱与塔柱作为分析对象;1# 过渡墩为分离式三柱矩形墩,评估时选取设置横向固定支座的中间墩柱以及设置双向活动支座的其中一个外侧墩柱作为分析对象。

表1 关键构件损伤状态与指标

2 易损性曲线建立方法

2.1 基本步骤

采用基于增量动力分析(incremental dynamic analysis,IDA)的能力需求比法来构建斜拉桥各关键构件的易损性曲线,步骤如下:

Step 1采用地震峰值加速度aPG作为地震动强度参数,根据表1确定各关键构件的损伤临界指标。

Step 2确定aPG的调幅原则和步长,按0.1g步长调整每条地震波为0.1g～1.0g(共10条)。

Step 3通过IDA计算背景工程各关键构件随aPG变化的地震需求SD与损伤临界值SC的比值,将该比值及其对应的aPG绘制在对数坐标系中,从而建立各关键构件SD/SC的对数IDA曲线。

Step 4采用式(1)、式(2),按照对数回归法拟合各关键构件的IDA曲线,获得回归均值λ及其标准差μ,然后根据式(3)计算第i个构件在不同地震强度下的损伤超越概率Pi:

λ=ln(SD/SC)=a[ln(aPG)]2+bln(aPG)+c

(1)

(2)

(3)

式中:a、b、c为回归系数;Sr为离散数据点相对于回归曲线的残差平方和。

Step 5重复Step 4,得到背景工程各关键构件的地震易损性曲线。

Step 6根据各关键构件的易损性曲线,采用特定的数学工具构建桥梁结构体系易损性曲线。

2.2 地震动

为了表征地震动的不确定性,地震易损性分析需要选取一定数量的地震波开展IDA。在一定范围内,地震波的数量越多越有利于提高易损性曲线的精度,但计算量会数倍增长。文献[16]表明,一般情况下采用10～20条地震波可以保证工程精度。根据背景工程地震安评报告所提供的设计反应谱,从PEER强震数据库匹配了20组II类场地实际地震加速度记录。图 5为20组地震波水平分量按照E2地震(aPG=0.177g)调幅后所对应的反应谱及平均谱曲线。斜拉桥横向抗震性能评估是笔者的研究重点,因此按照规范[13]采用横向+竖向的地震波输入模式。

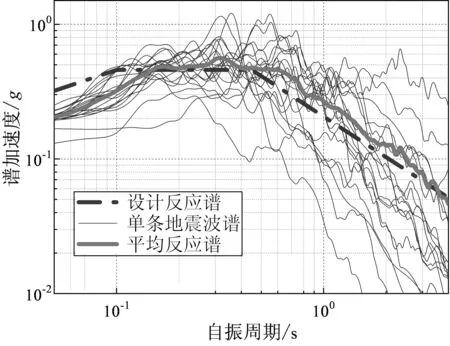
图5 地震动反应谱

3 基于构件易损性曲线的抗震分析

3.1 IDA曲线回归拟合

根据2.1节中的Step 1～Step 3得到各关键构件的对数IDA曲线,部分典型结果如图6。由于各条地震波频谱存在差异,构件在相同aPG下的地震响应有一定的离散性,但构件在同一损伤状态下的每条IDA曲线具有高度相似的变化规律。采用最小二乘非线性拟合方法对上述对数IDA曲线进行回归分析。根据式(3),得到拟合后ln(SD/SC)与ln(aPG)的关系曲线,如图6,拟合曲线的回归系数a、b、c如图7。

图6 典型构件损伤状态IDA曲线

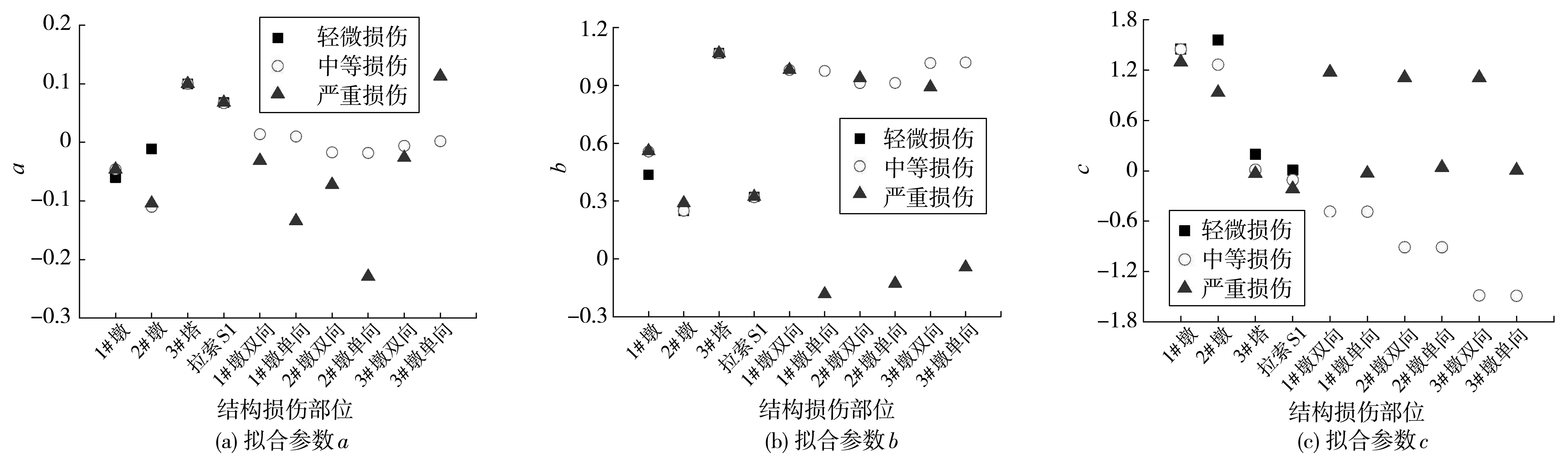
图7 各构件IDA曲线回归参数

3.2 构件易损性曲线分析

根据2.1节中的Step 4～Step 5,结合图7中的拟合公式得到各关键构件的地震易损性曲线,如图8。由于球型钢支座只界定了中等和严重两种损伤状态,因此图8(a)不包含支座的易损性曲线。由图8(a)可见,在相同aPG下,1# 过渡墩出现轻微损伤的超越概率最高,3# 主塔最低,2# 辅助墩和拉索介于两者之间。在所分析的aPG范围内,3# 塔的轻微损伤超越概率始终低于100%(最大约70%),而1# 墩的轻微损伤超越概率则在aPG=0.8g时达到100%。由图8(b)可知,在各个aPG下,球型钢支座出现中等损伤的超越概率始终位于前列,远高于2# 墩、拉索和3# 塔。在所有aPG范围内,2# 墩和3# 塔出现中等损伤的最大超越概率分别为80.36%和53.34%;而球型钢支座的中等损伤超越概率最早在aPG=0.5g时达到100%。由图8(c)可见,各关键构件出现严重损伤的超越概率在所有aPG范围内均低于100%,其中拉索出现严重损伤的超越概率最高可达94.89%,而3# 塔最低,其出现严重损伤的超越概率为45.67%。总体来看,在所有aPG范围内,背景工程的主塔出现各类损伤的超越概率均最低(即抗震富余度最高);在0～0.8g范围内,过渡墩出现轻微和严重损伤的超越概率最高;部分球型钢支座在所有aPG范围内出现中等损伤的超越概率最高。

图8 典型构件易损性曲线

根据桥址场地两水准设防地震动,图9进一步给出了各个关键构件出现3种损伤状态的超越概率水平,图9中的1# 双、1# 单指1# 过渡墩上的双向支座和单向支座,其余类推。由图9(a)可见,各关键构件在E1地震下出现3类损伤的超越概率总体较低(均低于35%),1# 墩出现轻微和严重损伤的超越概率相对最高,分别为26.39%和12.49%;1# 墩上的单向球型钢支座出现中等损伤的超越概率最高,为34.44%。图9(b)所反映的E2地震下的规律与图9(a)基本类似,但超越概率在数值上更大,如1# 墩出现轻微和严重损伤的超越概率分别为38.67%和18.54%,1# 墩上的单向球型钢支座出现中等损伤的超越概率达到50.03%。

由图9中超越概率的相对大小可知,各构件在E1和E2地震下出现轻微损伤的先后顺序为:1# 过渡墩→2# 辅助墩→斜拉索→3# 主塔;出现中等损伤的先后顺序为:1# 墩单向支座→2# 墩单向支座→1# 墩双向支座→2# 墩双向支座→3# 塔单向支座→1# 过渡墩→3# 塔双向支座→2# 辅助墩→斜拉索→3# 主塔;出现严重损伤的先后顺序为:1# 过渡墩→2# 辅助墩→3# 主塔→斜拉索→2# 墩单向支座→1# 墩单向支座→3# 塔单向支座→2# 墩双向支座→1# 墩双向支座→3# 塔双向支座。

图9 两水准地震下构件损伤超越概率

总体来看,边墩、过渡墩以及设置在它们上面的球型钢支座最容易出现各种程度的损伤,主塔和斜拉索相对较安全。这与斜拉桥的结构特点有关,由于主梁在横向具有较强的摆尾效应,过渡墩和边墩往往要承担很大的横向地震力,最容易成为抗震薄弱环节,而背景工程所采用的分离式桥墩更加剧了这一现象。因为设置横向固定支座的墩柱独自承担主梁的横向惯性力,而设置活动支座的墩柱仅通过球型钢支座的摩擦效应少量分担惯性力,这就造成固定墩容易受损而活动墩未得到发挥的不均衡后果。

4 基于体系易损性曲线的抗震分析

4.1 分析方法

3.2节从构件层面分析了斜拉桥的横向抗震性能,但这种分析显然忽略了各构件之间的关联作用。因此,从构件层面评估桥梁结构体系的抗震性能,有时会得到非保守的结论。根据各构件的损伤超越概率曲线,借助于联合概率分布函数可以得到桥梁体系的损伤超越概率,常用的方法包括一阶界限法和二阶界限法[17]。前者假设各构件损伤与否是相互独立的,后者则考虑了各构件发生损伤时存在相关性。一阶界限法根据各构件串联假设求解结构体系损伤超越概率的下限,根据各构件并联假设求解结构体系损伤超越概率的上限,即:

(4)

式中:Psys表示结构体系的损伤超越概率;Pi由式(1)—式(3)计算得到。二阶界限法在一阶界限法的基础上考虑各构件损伤超越概率之间的相关性,计算公式如式(5)—式(6):

(5)

(6)

式中:P1为结构体系内某一构件的损伤超越概率;Pij为结构体系内同时有i、j两个构件都出现损伤的超越概率;SDi、SDj分别为i、j两个构件的地震响应需求;SCi、SCj分别为i、j两个构件的损伤临界状态指标。

总体来说,一阶界限法相对保守,二阶界限法相对更精确,但其上、下限受各个构件之间相关性的影响较大,在应用中需要根据实际工程情况进行选用[18]。

4.2 构件易损性曲线分析

按照一阶和二阶界限法的计算公式得到如图10的桥梁体系易损性曲线的上、下限。由图10可见,对于本桥例来说,二阶界限法的带宽略小于一阶界限法。

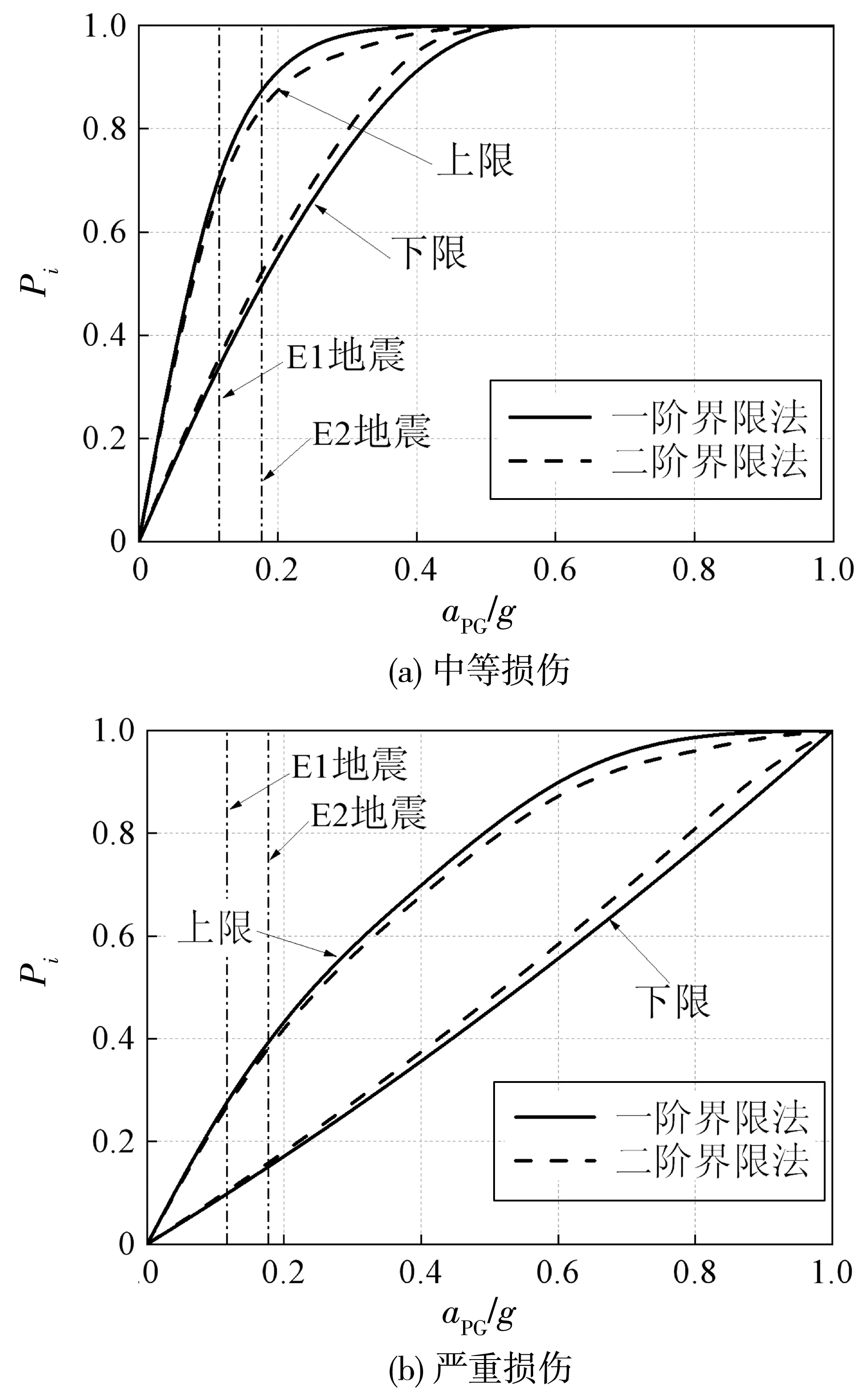
图10 体系易损性曲线

根据图10(a),桥梁体系在E1地震下出现中等损伤的超越概率区间分别为34.44%～75.64%(一阶界限法)、36.17%～72.61%(二阶界限法);在E2地震下对应的超越概率区间分别为50.03%～88.77%(一阶界限法)、52.53%～85.22%(二阶界限法)。可以看到,体系出现中等损伤的超越概率明显高于单个构件,如在E1、E2地震下,各构件出现中等损伤的超越概率最大值分别为34.44%、50.03%(均对应1# 墩单向支座),两者恰好是体系按一阶界限法得到的中等损伤超越概率下限值,且略低于二阶界限法的下限值。同理,由图10(b)可知,桥梁体系在E1地震下出现严重损伤的超越概率区间分别为9.74%～28.11%(一阶界限法)、10.23%～27.27%(二阶界限法);在E2地震下对应的超越概率区间分别为15.06%～39.69%(一阶界限法)、15.81%～38.50%(二阶界限法)。

上述分析表明,背景桥梁在两个设计水准地震作用下发生中等损伤的概率较高,但发生严重损伤的概率不高(体系和构件层面均不超过40%)。结合图9可知,体系存在较大的中等损伤风险主要是由球型钢支座抗震能力不足引起的,尤其是过渡墩和辅助墩上的支座在主梁摆尾效应下产生了很大的地震响应需求,这与很多已有研究结论[2-4]基本吻合。此外,背景桥梁的过渡墩和边墩采用分离式墩柱结构,大大削弱了桥墩的横向刚度,导致墩-梁刚度差进一步拉大,也可能是引起球型钢支座容易受损的原因之一。