Benchmark calculations and error cancelations for bond dissociation enthalpies of X—NO2

Jian Liu,Xudong He,Ying Xiong,Fude Nie ,Chaoyang Zhang

Institute of Chemical Materials,China Academy of Engineering Physics,P.O.Box 919-311,China

Keywords:Complex waveform scaling Analytical blast modeling Hopkinson-Cranz Scaled distance

ABSTRACT Safety plays an important role in determining the applicability of energetic compounds,and the bond dissociation enthalpy (BDE) of the “trigger bond” X-NO2 provides useful information to evaluate various safety properties.Accurate and rapid calculation of the BDE of X-NO2 is of great significance to perform the high-throughput design of energetic compounds,which becomes an increasingly popular means of materials design.We conduct a benchmark BDE calculation for 44 X-NO2 samples extracted from the iBond database,with the accuracies of 55 quantum chemistry calculation levels evaluated by the experimentally measured values.Only four levels have the global mean-absolute deviation (MAD) less than 10 kJ/mol,but no calculation level can achieve that all the local MADs of each category less than 10 kJ/mol.We propose a simple correction strategy for the original calculation deviations,and apply it to 30 calculation levels screened out through a series of accuracy assessments and obtain the corrected MAD<6 kJ/mol in some cases.We define a normalized time-cost(NTC)to evaluate the time-cost of each calculation level,and confirm that PBE0-D3/6-31G** (MAD=6.4 kJ/mol,NTC=0.8) works the best for most cases,followed by M062X/6-31g**,M062X/6-311g** and ɷB97XD/6-311g**,based on an insight into the accuracy-cost trade.The present work provides an accurate and fast solution for calculating XNO2 BDE via quantum chemical methods,and is expected to be beneficial to enhance the safety prediction efficiency of energetic compounds.

1.Introduction

Bond dissociation energy (BDE) is a quantitative descriptor of the strength of chemical bonds,providing useful information for understanding molecular stability[1].As for energetic compounds,many indicators of safety properties,such as impact sensitivity[2],shock sensitivity [3]and thermal stability [4],are strongly correlated with the dissociation energy of the weakest bond.Most energetic molecules contain nitro groups,and the weakest bond is mostly related to NO2,such as C-NO2,N-NO2,and O-NO2[5].Thereby,the weakest bond X—NO2(X=C,N and O)is regarded as the“trigger bond”[6],for its rupture starts decomposition[7].The BDE of the trigger bond is frequently considered as a quantitative index to evaluate the stability of energetic molecules.In general,a molecule will be stable under common conditions if the BDE >80 kJ/mol,and BDE>120 kJ/mol is required for practical application[8].

Experimentally,BDE is usually derived from the heat of formation (HOF) measurement,generally with a high accuracy within 1 kJ/mol [9].Consequently,the experimental BDEs of a few small molecules with no more than 10 heavy atoms are available only,and experimentally measured BDEs of polyatomic molecules have a typical uncertainty of±1—2 kcal/mol[10].For energetic molecules,it is more difficult to experimentally determinate BDEs,because of low vapor pressure[11]and radical instability[9].Hence,a reliable proposal is highly desired for achieving accurate BDE through theoretical calculations.

Over the past two decades,quantum chemistry methods have become powerful tools for calculating BDE of organic molecules[12].Izgorodina et al.[13]calculated BDEs of O-C,H-C,F-C and C-C bonds in a variety of molecules using density functional theory(DFT),Møller-Plesset perturbation theory (MP2) and high-level composite procedures.Solvation effects on the homolytic O-H BDEs of substituted phenols were studied using the UB3LYP/6—311++g(2df,p) method[14].For the homolytic cleavage of the—OH group of alcohols,the data provided by B3P86 method agrees well with the experimental determination,compared with that by B3LYP,B3PW91,B3P86,PBE1PBE[15].BDEs of benzene derivatives were calculated using DFT and correlated substituent effects on BDEs using conventional Hammett sigma constants [16].Zheng et al.[17]calculated the N-N BDEs using 8 composite high-levelab initiomethods and 25 DFT methods,and concluded that the M05-2X method can provide the most accurate results.Li et al.[18]compared methods for the BDE calculations,including G4 (MP2),DHDFT,M06-2X and B3P86.Accurate homolytic N-H,N-Cl and N-Br BDEs were obtained by the high-level W2 thermochemical protocol[19,20].Benchmark DFT studies were performed on the C-CN homolytic cleavage,with the substituents effect on the BDE for nitriles screened [21].Du et al.[12]examined the reliability of a series of methods for the prediction of O-CH3BDEs with a sample set of 25 aromatic and non-aromatic molecules.Gabriel et al.[22]presented a benchmark investigation on the O-H BDEs for gallic acid,by DFT,MP2,coupled-cluster with single and double excitations (CCSD),and coupled cluster with single,double and triple excitations(CCSDT) [23].

It is challenging to obtain accurate BDEs by quantum chemical calculations,partly because the same accuracy needs to achieved for both the target molecule and its homolysis radicals in dealing with the electron correlations [11,24].Among all those methods,CCSDT is generally regarded as the most accurate but infeasible for large molecules,because the computation cost scales up by the eighth power of the molecular size,e.g.,as O(N8) [25].Therefore,CCSDT is usually used to evaluate the accuracy of the other methods,with small molecules as test set[1,9,11,13,18—20,26—32].In comparison,DFT is more efficient with a magnitude as O(N4),and thus available for larger molecules[33].The choice of different DFT method may greatly affect the computational accuracy of BDE,so a systematic assessment of various DFT methods are indispensable for a special group of system.Unfortunately,no systematic evaluation has been presented so far for the X-NO2bonds.Most of those BDE calculation studies for nitro molecules are merely dedicated to use the calculated values as criterions to evaluate the stability of novel designed molecules [4,8,34—38],or as a descriptor to train quantitative the structure-sensitivity relationships [39—48].

The goal of this work is to determine whether there are methods suitable for calculating X-NO2BDEs with low cost and high accuracy,by performing benchmark calculations via quantum chemistry methods and introducing a correction strategy.Both accuracy and cost are considered,following the concept of high-throughput calculation (HTC) [49—51]that derived from Materials Genome Initiative [52].The more accurateness is helpful to determine whether a nitro molecule has practical applicability as an energetic molecule,and the less computational cost is conducive to screen a large quantity of energetic molecules efficiently.Thereby,a rational trade-off between them will accelerate the discovery of novel energetic molecules.Herein,the present work is divided into sections of accuracy evaluation,error cancelation and trade-off between accuracy and cost.

The dataset of the current work is made up of 44 nitro molecules with experimentally measured X-NO2BDEs,which are extracted from theiBonddatabase [53].A total of 55 calculation levels is employed in this work,including 12 DFT functionals,MP2 and 3 complete basis set (CBS) methods,with 4 basis sets considered in the DFT calculations.A total of 30 calculation levels is screened out by series of accuracy assessments with respect to functional,basis set and X-NO2category.By comparison,we propose a simple strategy to correct the systematic deviation.The parameters of the deviation formula at each level are automatically fitted in batches,by a fitting toolkit currently developed by our team.The trade-off between accuracy and cost indicates that PBE0-D3/6-31G**should be the best choice in most cases,and M062X/6-31g**,M062X/6-311g**and ω B97XD/6-311g**are recommended unless mean-absolute deviation (MAD) <6 kJ/mol required.This work provides an accurate and fast solution for calculating BDE of X-NO2using quantum chemical methods,and is helpful to evaluate the stability of NO2molecules,and further to search new ones.

2.Computational methods

2.1.Workflow for dataset construction

The X-NO2BDEs calculated at each level were obtained through 3 main procedures,namely,sample collection,conformer searching and BDE calculation (Fig.1).Firstly,the BDEs of X-NO2were searched out from theiBonddatabase [53]and saved as pairs of molecular structure and experimentally measured X-NO2BDE.Secondly,a conformer searching was implemented to confirm the most energetically favored one for each molecule.Thereby,the XNO2BDE was calculated at various levels.

2.2.Sample collection

In this work,the experimental data were used as the criterion to evaluate the accuracy of different quantum chemistry methods,and all the nitro molecules and the measured X-NO2BDEs were collected from theiBond[51]database,within an element range of C,H,N and O,which make up a common energetic molecule.

2.3.Conformer searching

To provide an energetically favored conformer for subsequent quantum chemistry calculations,each of the above 44 molecules underwent a conformer searching procedure,including conformer sampling,geometry optimization and energy ranking.Conformer sampling was implemented by systematic grid scanning,in which all the torsion angles of a molecule rotate intermittently from 0°to 360°at an interval of 12°.The universal force field (UFF) [54]was adopted at the geometry optimization stage,and the local optimal structure and potential energy of each conformer sample were obtained through energy minimization with a maximum iteration of 5000 steps.Afterwards,the conformer with the lowest potential energy was selected for subsequent quantum chemistry calculations.Because the molecular force field method is infeasible to radicals,the initial conformer of each radical was extracted from its neutral parent,which had been achieved by geometry optimization and frequency confirmation in advance.The conformer searching was performed with Materials Studio software [55].

2.4.BDE calculation

The X-NO2BDE of a nitro molecule can be defined as the enthalpy change of the reaction (1) in the gas phase at 1 atm and 298.15 K.

The enthalpy of formation for each species is calculated using

whereZPErepresents the zero-point energy,Htans,Hrot,andHvipare the standard temperature correction terms calculated using the equilibrium statistical mechanics with harmonic oscillator and rigid rotor approximations.

In the benchmark calculations,MP2[56],three complete-basisset (CBS) series including CBS-QB3 [57],CBS-Q [58],and CBS-4M[59],as well as the 12 DFT methods including M06-2X [60],M11[61],PBE[62],PBE0[63],PW91[64],B3PW91[65],B3LYP[66],PBED3,PBE0-D3,B3PW91-D3,B3LYP-D3 [67],and ɷB97XD [61],were adopted.Using the lower cost levels to reduce computational cost was not considered in performing the calculations of geometry optimization and the frequency calculation.A uniform setting was employed in the structural optimization,frequency calculation and single point energy calculation at each calculation level.Because the option of basis sets cannot be ignored in discussing the accuracy-cost trade-off,4 commonly used basis sets were employed,including 6—31g**,6—311g**,cc-pvdz,and def2-tzvp.More sophisticated methods and larger basis sets were not considered,even though they might enhance the computational accuracy,due to the main purpose of this study that is to achieve accuracy-cost traded-off methods for calculating X-NO2BDE,instead of the more accurate ones.

2.5.Error cancelation strategy

Error cancelation for each calculation level was performed using the simplest linear equation of the first order.We assumed that the calculated values will generally be underestimated,and added an additional positive deviation compensation term for the category of molecules exhibiting obvious overestimation.The equation is expressed as:

whereE′is the corrected BDE value,Eis the BDE obtained from a quantum chemistry calculation level,α,β1,and β2are parameters required to be fitted,andC(equal to 0 or 1) works as a switch for specific categories of X-NO2bonds to provide positive deviation compensation.For a X-NO2category that needs positive deviation compensation,all the molecules of this category were set toC=1,whileC=0 were set for the others.

2.6.Time-cost tradeoff evaluation

A normalized time-cost(NTC)was applied to evaluate the timecost tradeoff of each calculation level,and expressed as:

where l represents the calculation level,irepresents the molecule or radical being calculated,nis the total number of molecules and radicals,Tliis the time-cost for calculating molecule or radicaliat level l,andTsiis the time-cost for calculating molecule or radicaliat the reference level s,i.e.,B3LYP/6-31g**in the current work.

2.7.Software and tools

The pre-and post-DFT treatments were automatically performed by a high-throughput software package Energetic Molecular Design Engine [68],developed by our team.All the quantum chemistry calculations were performed by the Gaussian 09 programs[69].The fitting to get correction formulas was performed by a toolkit named PSOFit.pl(Table S10),developed by us too,which is capable of automatically fitting curves in batches based on the Particle Swarm Optimization algorithm [70].

3.Results and discussion

3.1.Samples of dataset

A total of 44 X-NO2samples includes 22 C-NO2(Table 1),10 Ar-NO2(Table 2),8 N-NO2(Table 3),and 4 O-NO2(Table 4) bonds.Those bonds each linking with a nitro group and an aromatic ring are specifically classified as Ar-NO2,because their BDEs subsequently calculated via various quantum chemistry methods exhibit less accuracy than those of other types.That is,it needs a separate discussion.

Table 2 BDEexp(in kJ/mol) of Ar-NO2.

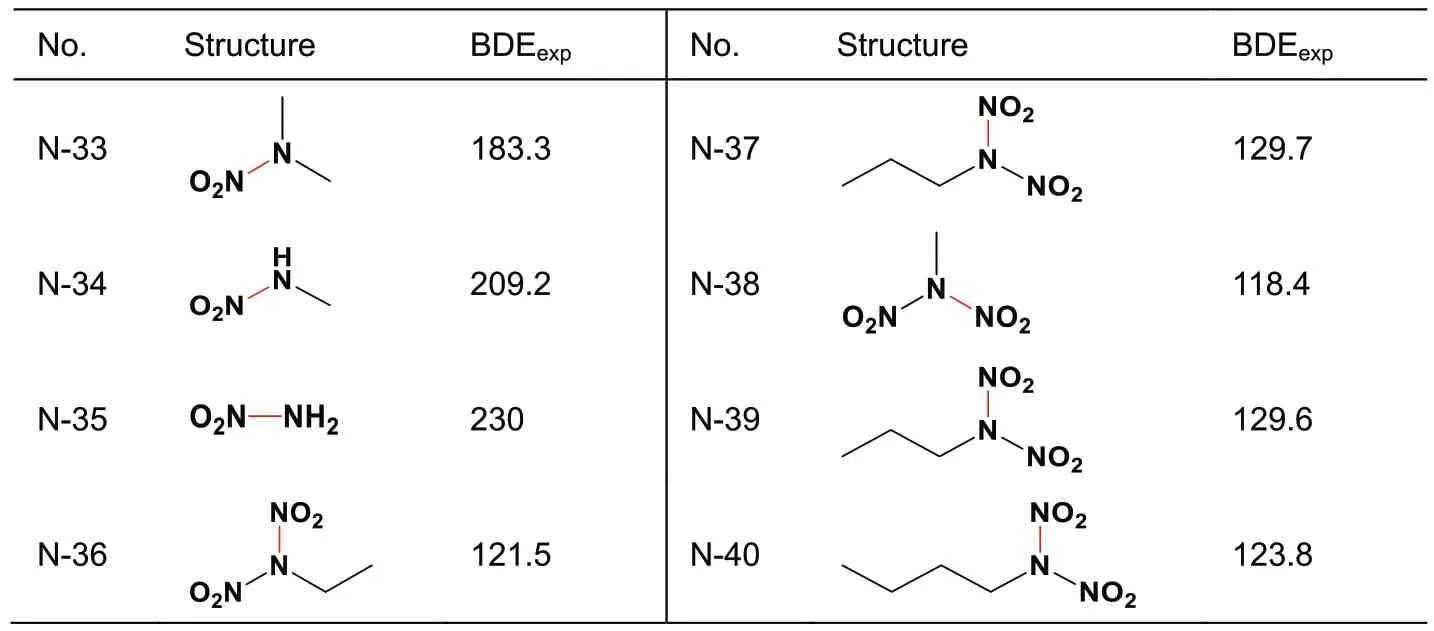
Table 3 BDEexp(in kJ/mol) of N-NO2.

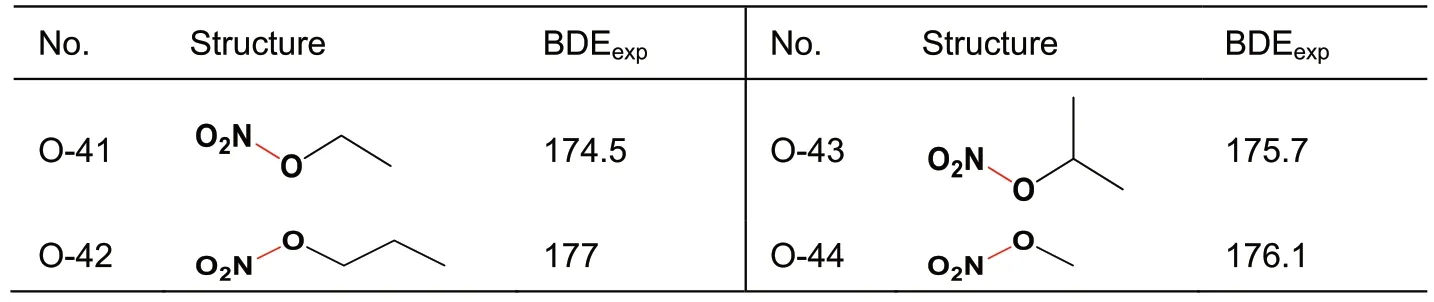
Table 4 BDEexp(in kJ/mol) of O-NO2.

3.2.Accuracy evaluation

The X-NO2BDEs of all the 44 molecules calculated at the 55 levels are illustrated as the parity plots in Fig.2,and the meansigned deviation (MSD),MAD,root-mean-square deviation(RMSD)and coefficient of determination(R2)are shown in Table 5.

The rough agreement between BDEcalcand BDEexpcan be observed from the outlines of the parity plots in Fig.2.For the three CBS methods,the results of both CBS-4M and CBS-QB3 are in good agreement,while CBS-Q presents obvious positive deviations for several molecules.In general,the M062X,M11 andɷB97XD calculation results agree well with the experimental measurements.M062X and M11 are comparable to CBS-4M and CBS-QB3,while inferior toɷB97XD.The calculated X-NO2BDEs by MP2 exhibit huge positive deviations compared with the experimental values (Fig.2),with MADs of 43(6—31g**),41(6—311g**),38(ccpvdz)and 66 kJ/mol(def2-tzvp)(Table 5).According to the findings of other researchers,MP2 are often less reliable because of the spin contamination in dealing with radical species[71,72].Recent work by Aquino et al.[12]reported that MP2/def2-TZVP was failed to calculate O-CH3BDEs for both of aromatic systems(MAD=144 kJ/mol) and nonaromatic systems (MAD=24 kJ/mol).These results indicate that MP2 is not suitable for predicting X-NO2BDE.Therefore,MP2 and CBS-Q will not be mentioned in the following discussion.

Systematic negative deviations can be seen from the results of PBE,PBE0,B3PW91 and B3LYP.They can be well corrected by introducing the D3 dispersion correction,as shown in Fig.2.The D3 correction can enhance the accuracy of the functionals without additional computational cost,and is strongly recommended for BDE calculations.Therefore,in the following discussion,it will exclude the results of these four functionals without D3 correction.

The influence of basis set is also evaluated by the MAD.As shown in Fig.3,for PBE-D3 and PBE0-D3,no significant difference in the MAD is exhibited;as toɷB97XD,PW91,B3LYP-D3 and B3PW91-D3,the basis set 6—31g**works the best,while def2-tzvp the worst;in comparison,M062X and M11 produce deviations reverse to each other.Fig.3 also indicates that def2-tzvp is less accurate than the other 3 basis sets,unless collaborated with M062X.Thus,the predication based on the four functionals and def2-tzvp basis set is not only costly but also inaccurate.

Also,the MAD is employed to evaluated the applicability of methods at various levels to different X-NO2categories (Fig.4and Table 6).No level can guarantee all the individual MAD of any category <10 kJ/mol,even though the whole MADs of four levels reach this criterion.For C-NO2,the most accurate method is CBS-4M (MAD=6.6 kJ/mol),while PW91,B3LYP-D3 or PBE-D3 doesn't work well,with MAD >10 kJ/mol.For Ar-NO2,the most accurate method is B3LYP-D3/6-311g**(MAD=8.0 kJ/mol),which works much better than M062X,M11 orɷB97XD (MAD >10 kJ/mol).The most accurate methods for the N-NO2and O-NO2are PBE-D3/def2-tzvp(MAD=4.7 kJ/mol)and CBS-4M(MAD=1.8 kJ/mol),respectively.The higher accuracy of CBS-4M is exhibited when dealing with C-NO2and O-NO2,while it produces the less accurate results for Ar-NO2(MAD>21 kJ/mol)and N-NO2(MAD>13 kJ/mol).These large deviations are consistent with the previous reports,as the spin-contamination exists and most of theab initiomethods are not capable of dealing with the open-shell systems due to the spin-contamination problem[17,20,25,27,73].Hence,the DFT methods should be better choices for calculating Ar-NO2BDE.

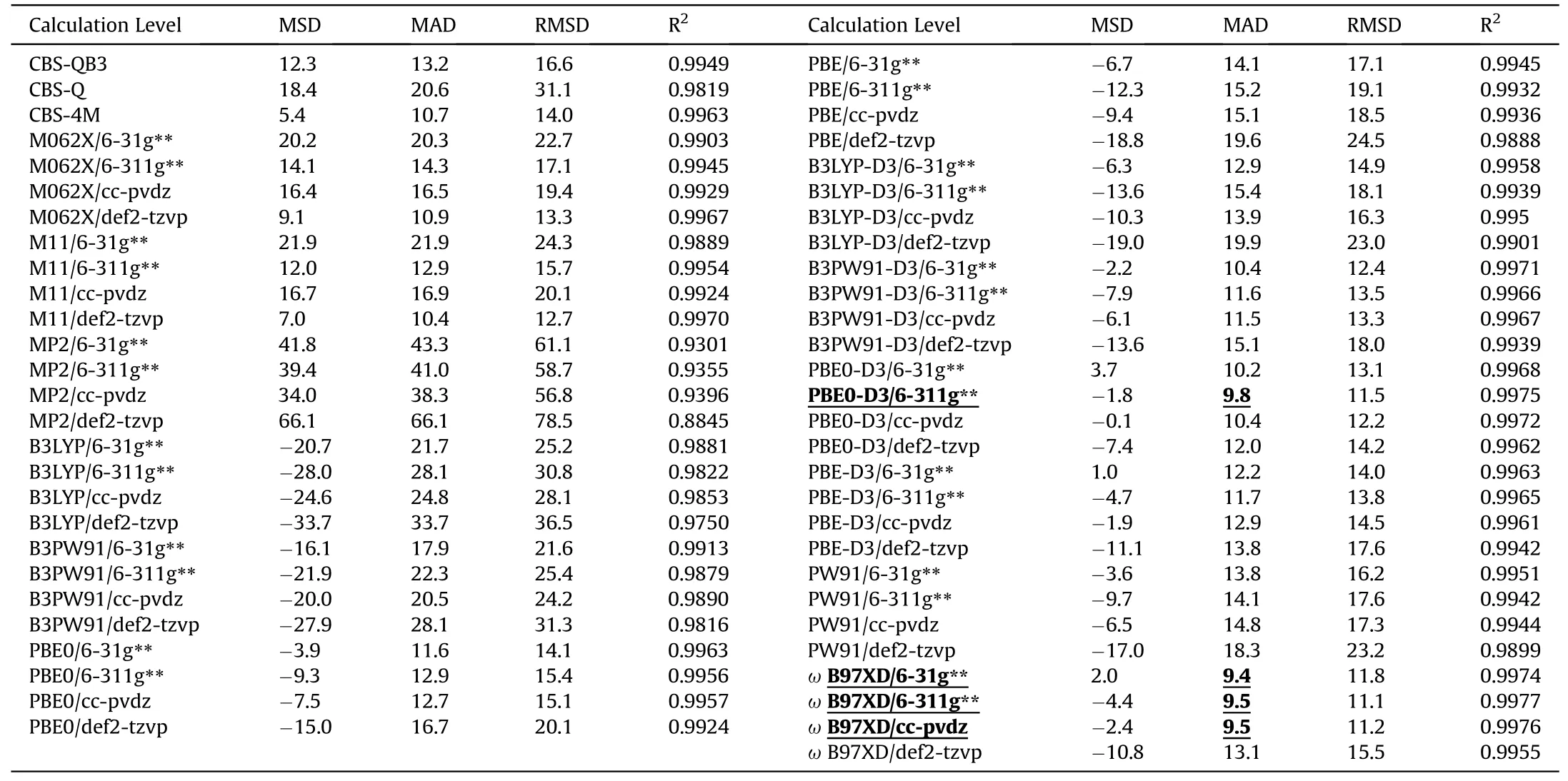
Table 5 Statistical results for the performance of theoretical levels for calculating the X-NO2 BDEs (MSD,MAD and RMSD are in kJ/mol).

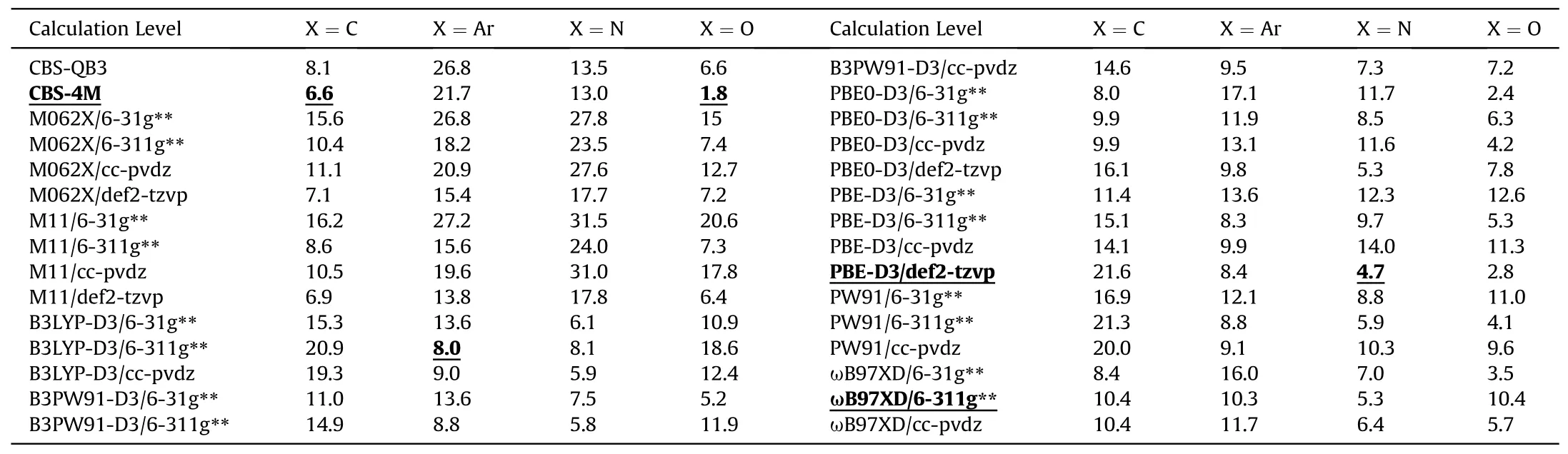
Table 6 MADs of various BDE calculation levels (kJ/mol).

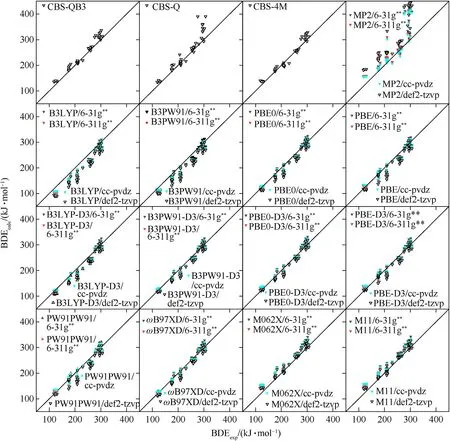
Fig.2.Parity plots of BDEcalc against BDEexp.

3.3.Error cancelation

In order to develop a feasible strategy to reduce the aforementioned deviation of the X-NO2BDE,we pay attention to more deviation information like deviation distribution.Therefore,a heat map for signed deviation is illustrated in Fig.5 to show the distribution of the calculated BDE deviations in terms of the calculation level and the X-NO2type.

Fig.5 indicates that the cases located by calculation levels and molecule numbers,with deviation >10 kJ/mol or <-10 kJ/mol accounted for a higher proportion,and systematic positive or negative deviation with respect to certain calculation levels and dissociation bond categories.The calculation levels can be easily divided into three groups based on the X-NO2categories and the types of systematic deviation.Group I covers CBS-QB3,CBS-4M,M062X/(6—31g**,6—311g**,cc-pvdz and def2-tzvp) and M11/(6—31g**,6—311g**,cc-pvdz and def2-tzvp),and the BDEs calculated at these levels exhibit systematic positive deviations for Ar-NO2,tri-nitro C-NO2and alkene C-NO2.Group II contains PBE0-D3/(6—31g**,6—311g**,cc-pvdz and def2-tzvp),PBE-D3/(6—31g**,6—311g**,cc-pvdz and def2-tzvp),and PW91/(6—31g**,6—311g**and cc-pvdz),and the calculated BDEs are fallen in systematic negative deviations for C-NO2(except for tri-nitro C-NO2andalkene C-NO2).B3LYP-D3/(6—31g**,6—311g** and cc-pvdz),B3PW91-D3/(6—31g**,6—311g** and cc-pvdz),andɷB97XD/(6—31g**,6—311g**and cc-pvdz)are included in Group III,and the predicted BDEs show systematic negative deviations for O-NO2and C-NO2(except for tri-nitro C-NO2and alkene C-NO2).Meanwhile,there are several unusual cases,such as the molecules C-14,Ar-25 and Ar-30,whose deviation changes along a different tendency of the others in the same category,and the negative deviations of B3LYP-D3/6-31g** cover almost all bond categories.

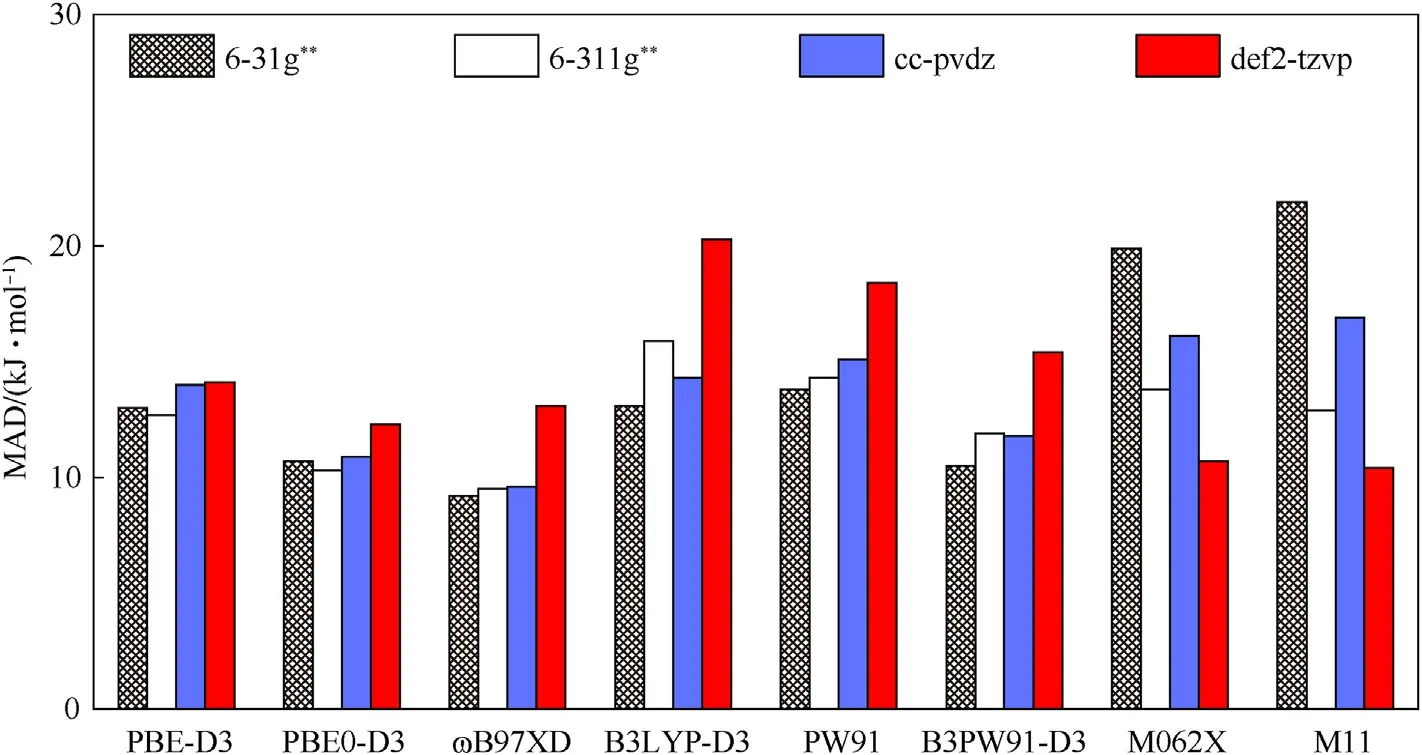
Fig.3.MADs of X-NO2 BDE calculated by various combinations of basis sets and functionals.

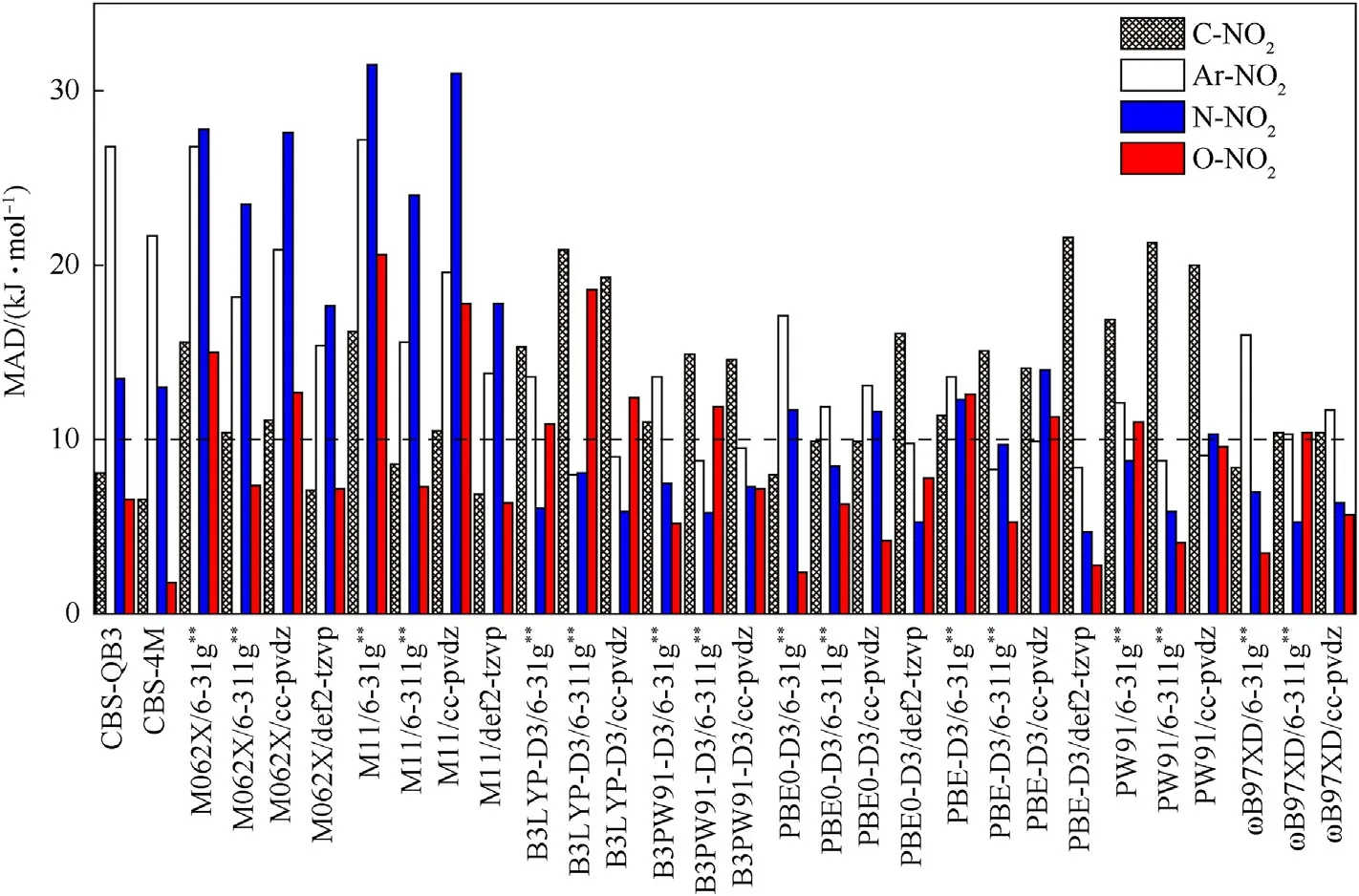
Fig.4.MADs of each calculation level based on X-NO2 categories.

According to the above discussion,30 calculation levels are divided to three groups,and descriptor C to 1 is set as samples for additional systematic correction (Table 7).The parameters for the correction formulas of the 30 calculation levels are fitted according to Eq.(3),by employing thePSOFit.pl(Table 8).The corrected BDEs on the 30 calculation levels are illustrated in Fig.6 by a new heat map for signed deviations.Fig.6 shows the circumstances with deviations ranged from -10 to 10 kJ/mol.Thereby,most of the deviations have been lessened through our correction strategy.However,for the unusual molecules C-14,Ar-25 and Ar-30,the negative deviations at all calculation levels are still >10 kJ/mol.It should be noted that there is uncertainty for employing experimentally measured values as criterion to evaluate calculation deviations,as many previous studies reported that the experimental BDE sometimes has a typical uncertainty of 4—8 kJ/mol [1,74].Therefore,there is a high probability that the effectiveness of the current strategy is disturbed by the large errors from experimental samples such as C-14,Ar-25 and Ar-30.

Table 7 Correction strategies for X-NO2 BDEs.

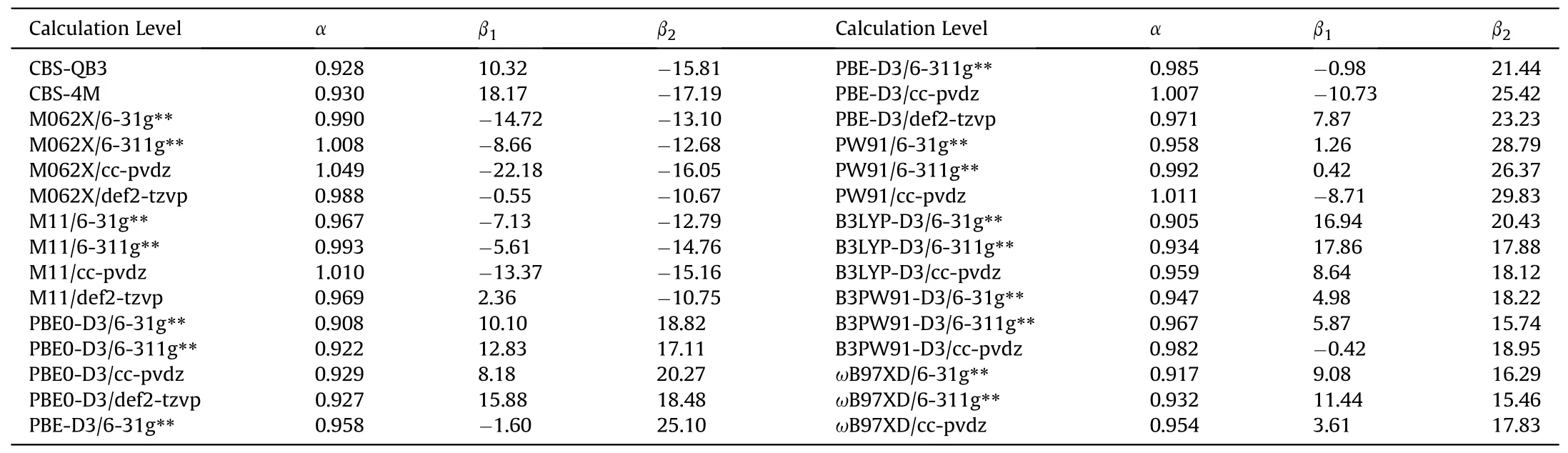
Table 8 Parameters of Eq.(3) for each calculation level.

As shown in Fig.7,the MADs on all the calculation levels can be improved to<10 kJ/mol,validating the present correction strategy too.By the error cancelation,the 4 most accurate levels are CBSQB3 (MAD=5.3 kJ/mol),M062X/6-31g** (MAD=5.6 kJ/mol),M062X/6-311g** (MAD=5.6 kJ/mol) andɷB97XD/6-311g**(MAD=5.6 kJ/mol).

3.4.Trade-off between accuracy and cost

To quantitatively evaluate the accuracy-cost tradeoff,the dependence of the MAD and NTC normalized from the time consumption at various calculation methods is considered.As illustrated in Fig.8,despite the highest accuracy of CBS-QB3,its CPU-cost is remarkably large (NTC >40),significantly higher than those at all the other calculation levels.The time cost of the five calculation levels using def2-tzvp basis set is only lower than that of CBS-QB3,but their accuracy has no obvious advantage among all the 30 calculation levels.Three calculation levels of M062X/6-31g**,M062X/6-311g**andɷB97XD/6-311g**possess an accuracy(MAD=5.6 kJ/mol)only slightly lower than that of CBS-QB3,which cost much less CPU-time (NTC=1.5,1.6 and 1.4,respectively).PBE0-D3/6-31g**consumes the least time(NTC=0.8)and exhibits a moderate accuracy(MAD=6.4 kJ/mol).In a word,CBS-QB3 is too costly to be accepted despite the highest accuracy,and the def2-tzvp basis set is not recommended,due to no advantage in either accuracy or cost.In the most cases,PBE0-D3/6-31G**should be the best choice,and the other three levels of M062X/6-31g**,M062X/6-311g** andɷB97XD/6-311g** are recommended too,unless the MAD <6 kJ/mol required.

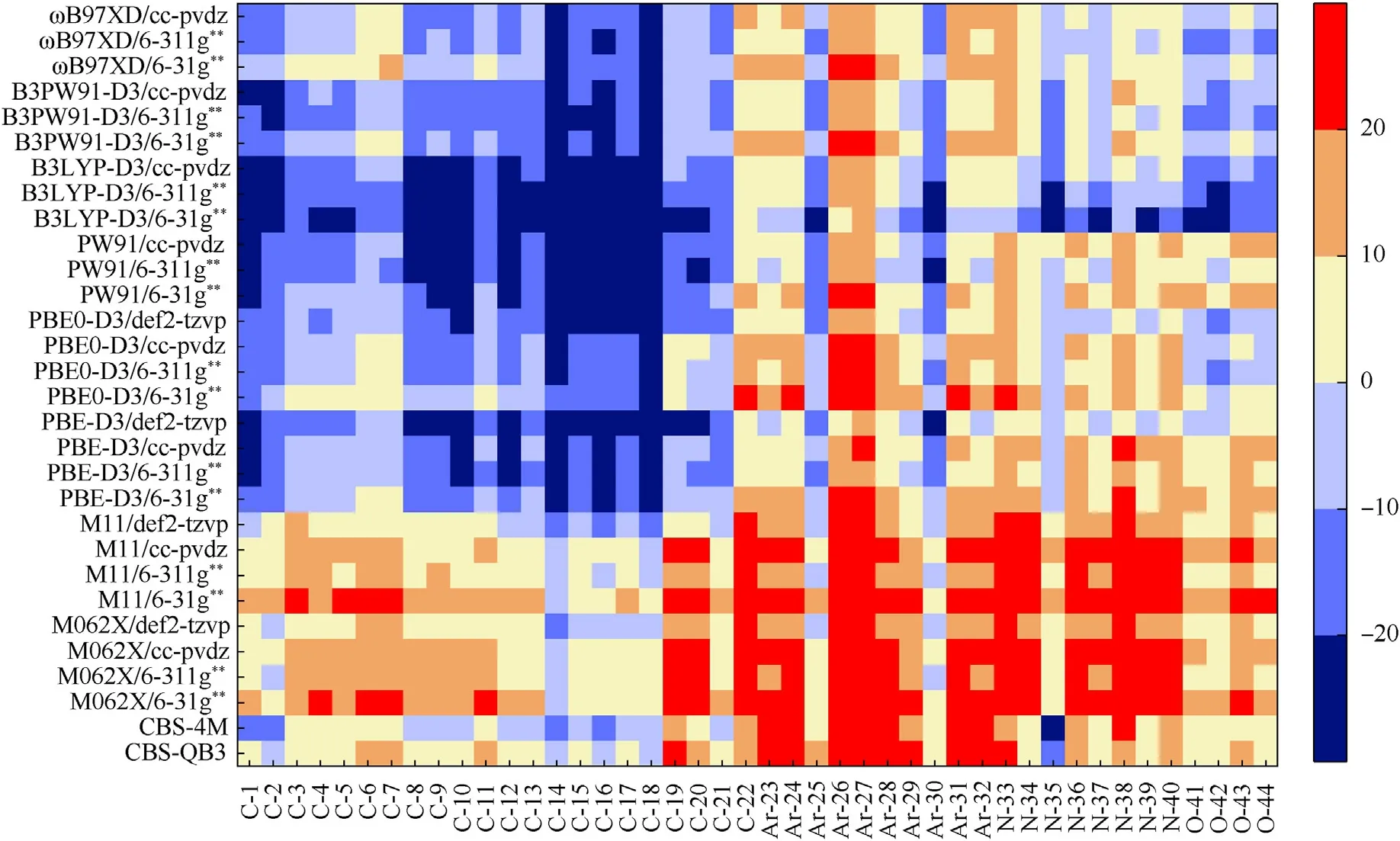
Fig.5.Heat map of signed deviation (in kJ/mol) with respect to the calculation level and X-NO2 type.

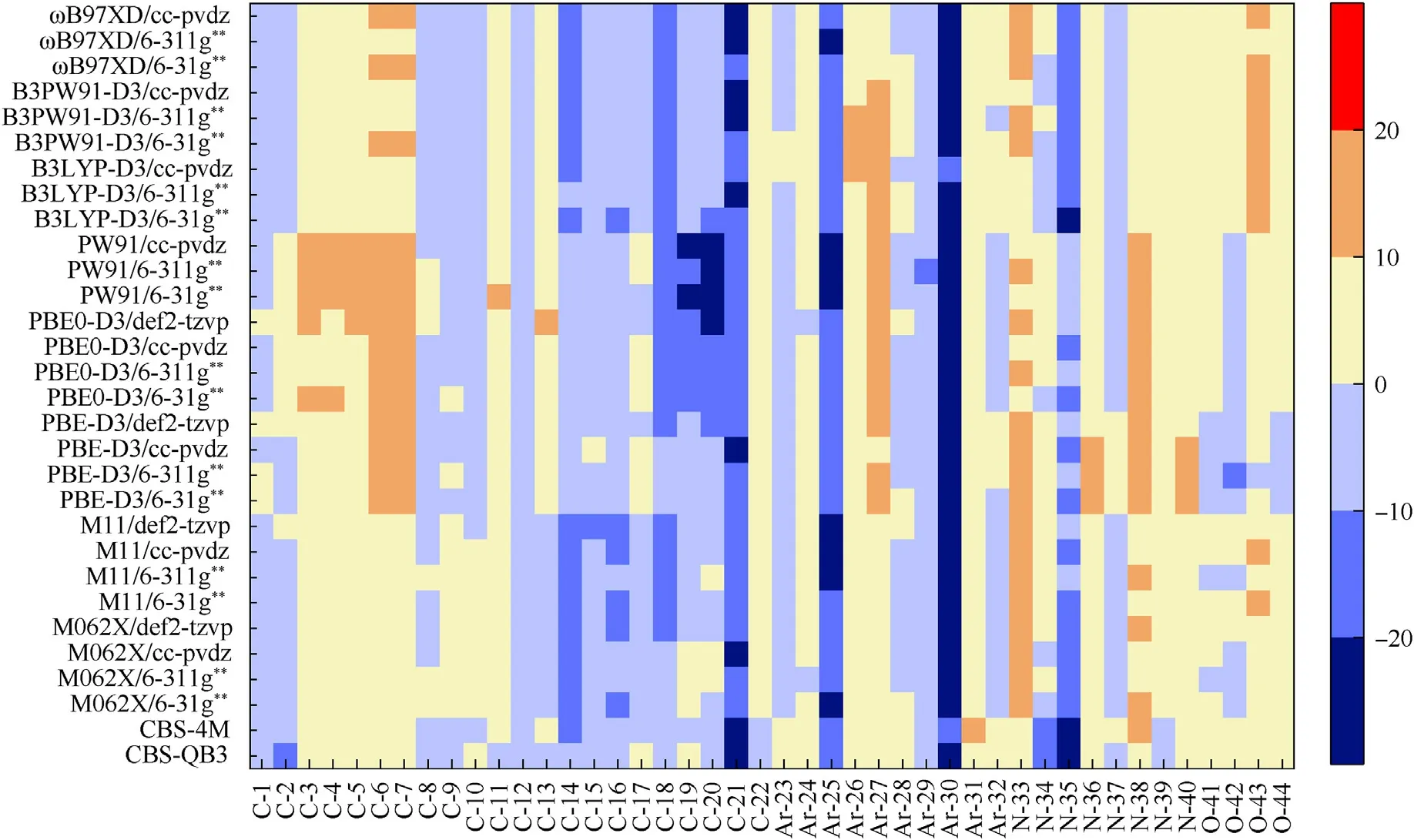
Fig.6.Heat map of signed BDE deviation (in kJ/mol) after correction.

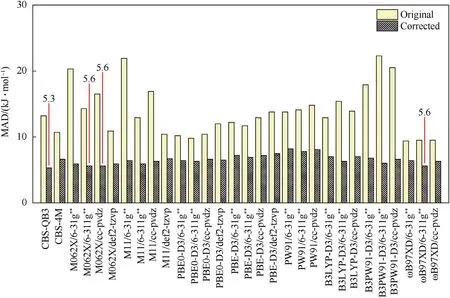
Fig.7.Comparison in original and corrected MADs on various calculation levels.

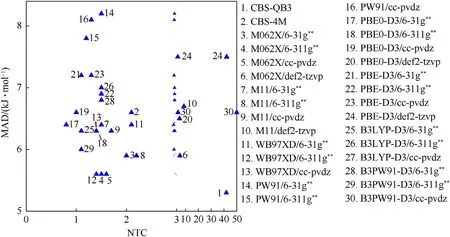
Fig.8.Dependence of MAD vs.NTC.

4.Conclusions

To confirm quantum chemistry methods with high accuracy and low cost for calculating X-NO2BDEs,55 common calculation levels are applied to 44 molecules collected from theiBonddatabase,with experimentally measured BDE as reference.Considering the accuracy-cost tradeoff,four theoretical levels of PBE0-D3/6-31G**,M062X/6-31g**,M062X/6-311g** andɷB97XD/6-311g** are validated with a whole MAD <10 kJ/mol for the full dataset,and recommended for high-throughput calculations.However,no calculation level can achieve that all the local MADs of each category<10 kJ/mol.Furthermore,a strategy for correcting the calculation deviations is presented as it can lessen the deviations as much as MAD <6 kJ/mol.This work recommends the theoretical levels to achieve accurate BDEs of X-NO2bonds while with moderate cost,beneficial to accelerate the screening and discovering of energetic NO2molecules.

Author contributions

The manuscript was written with contributions from all authors.All authors have given approval to the final version of the manuscript.

Data and software availability

All the original data and the codes forPSOFit.plare available at the Supporting Information.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

The authors gratefully acknowledge the support of the Science Challenge Project (TZ-2018004).

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.dt.2021.11.014.