不同MMSE 评分下阿尔兹海默病发病风险因素的贝叶斯分位数回归联合模型分析

王廉源, 杨 毅, 丛慧文, 王浩桦, 包绮晗, 李承圣, 周立雯, 丁子琛, 李艳丽, 石福艳, 王素珍

（1.潍坊医学院公共卫生学院卫生统计学教研室，山东 潍坊 261053；2.潍坊医学院图书馆，山东 潍坊 261053）

近几年，随着人均寿命不断地增加，人口老龄化问题愈发明显，我国阿尔兹海默病（Alzheimer’s disease，AD）患病人数不断增加［1］，成为继心血管疾病和肿瘤之后导致老年人死亡的第三大病因［2-3］。相关研究［4］表明：2015 年中国痴呆症患病人数约为950 万。到2050 年，中国痴呆症患病人数预计会达到约2 800 万，AD 将成为全球最大的公共卫生问题。AD 病因复杂，许多研究者借助如Cox 模型等单一的传统统计学方法对AD 病因进行探索性研究［5-7］。研究［8-9］表明：简易精神状态检查（Mini-Mental State Examination，MMSE）量表可预测AD 的当前阶段及其发展趋势。但是MMSE等标记物轨迹变化复杂，并受年龄和载脂蛋白E（apolipoprotein E，APOE）状态的相互作用，受试者体内的生物标志物变化率与MMSE 恶化相关［9］。因此，探讨AD 发展的影响因素，需考虑MMSE的轨迹变化。研究者选择分位数回归（quantile regression，QR）模型对MMSE 各个分位数处的影响因素进行探讨分析［10-14］。然而，QR 仅可分析不同分位点MMSE 的影响因素，不能分析MMSE 各分位点处各变量与AD 的关联性。针对该问题，有学者提出基于贝叶斯方法的分位数联合模型方法可以克服使用单一技术时造成的损失和经典联合模型的参数估计方法容易产生偏差的缺点，可以探讨生物标记物与时间-终点事件之间的关联性［15］。鉴于此，本研究拟基于MMSE 评分的分位数回归模型构建贝叶斯分位数联合模型的纵向子模型，基于Cox 比例风险模型构建联合模型的生存子模型，进而探索分析不同MMSE 评分下的AD 发病风险因素，通过比较不同分位数下MMSE 评分相同风险因素作用程度的差异，进而为AD 的预防和个性化诊断提供参考。

1 资料与方法

1.1 数据来源及筛选标准本研究使用数据来源于AD 神 经 成 像 计 划 （Alzheimer’s Disease Neuroimaging Initiative，ADNI）数 据库。研究对象的纳入标准：2005—2016 年接受随访的正常受访者。排除标准：①缺乏MMSE 评分信息；②缺乏完整的临床和流行病学信息；③入组时已患AD。

1.2 主要变量及其筛选参阅国内外文献，结合临床专家意见，拟采用LASSO 回归分析方法消除变量的多重共线性，对变量进行筛选［16］。本研究拟纳入的主要变量：年龄、性别、婚姻、教育程度评分、种族、载脂蛋白E4 （apolipoprotein E4，APOE4）基因、家族史、舒张压、收缩压、血糖浓度、总胆固醇、总甘油三酯、白蛋白和MMSE评分。本研究将种族分为白种人和其他种族；将婚姻状况分为已婚和其他。本研究的结局事件是患有AD。

1.3 统计学分析采用LASSO 回归方法消除变量间的多重共线性，纵向数据分别采用分位数回归模型和Cox 回归模型进行单因素和多因素分析，选择贝叶斯分位数联合模型进行联合模型建模分析。采用SPSS 22.0 软件进行统计描述，连续性变量（总胆固醇和收缩压等）以±s表示，分类变量（性别和种族等）以百分比表示；采用R 4.1.2 软件的lars 包进行LASSO 回归，分别用lqmm 包的lqmm 函数和Survival 包的coxph 函数进行分位数回归模型和Cox 回归模型，贝叶斯分位数联合模型采用BQt 包的qrjm.BQ 函数进行分析。所有统计检验均为双侧检验，检验标准为α=0.05。

2 结 果

2.1 受试者一般情况本研究所用的ADNI 数据集包含425 名随访者，其中79 名随访者随访结束时发生AD。随访者的平均随访时间为（1.85±1.43）年，平均随访次数为（2.55±0.69）次。随访结束时男性223 人（52.47%），女性202 人（47.53%）；MMSE 评 分 2～30 分，平 均 为（27.69±2.69）分；425 名随访者的平均年龄为（72.06±7.24）岁，见表1。425 名随访者随访结束时MMSE 评分的分布情况见图1。由图1 可知，MMSE 评分的分布存在严重的厚尾情况。

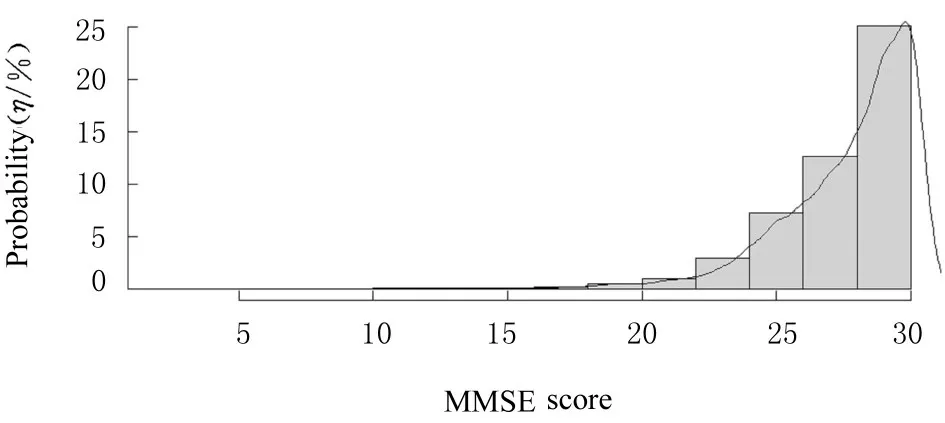
图1 425 名随访者MMSE 评分分布情况Fig.1 Distribution of MMSE scores of 425 interviewers

表1 425 名随访者的基本情况Tab.1 Basic informations of 425 interviewers

2.2 主要变量筛选结果采用LASSO 回归方法对研究的13 个变量进行筛选分析，结果见表2 和图2。由图2 可知，在第12 步时，Cp 值最小。因此，最终纳入研究的变量总共有10 个，分别为白蛋白、总胆固醇、血糖浓度、收缩压、年龄、教育程度评分、APOE4 基因、家族史、性别和种族，排除变量有3 个，包括舒张压、婚姻和甘油三酯，具体赋值情况见表2。

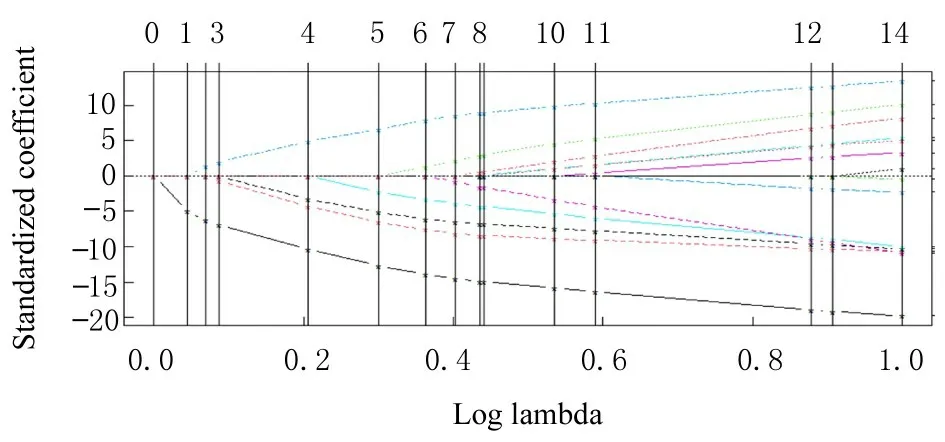
图2 拟纳入变量LASSO 回归分析结果Fig.2 LASSO regression results for proposed inclusion variables

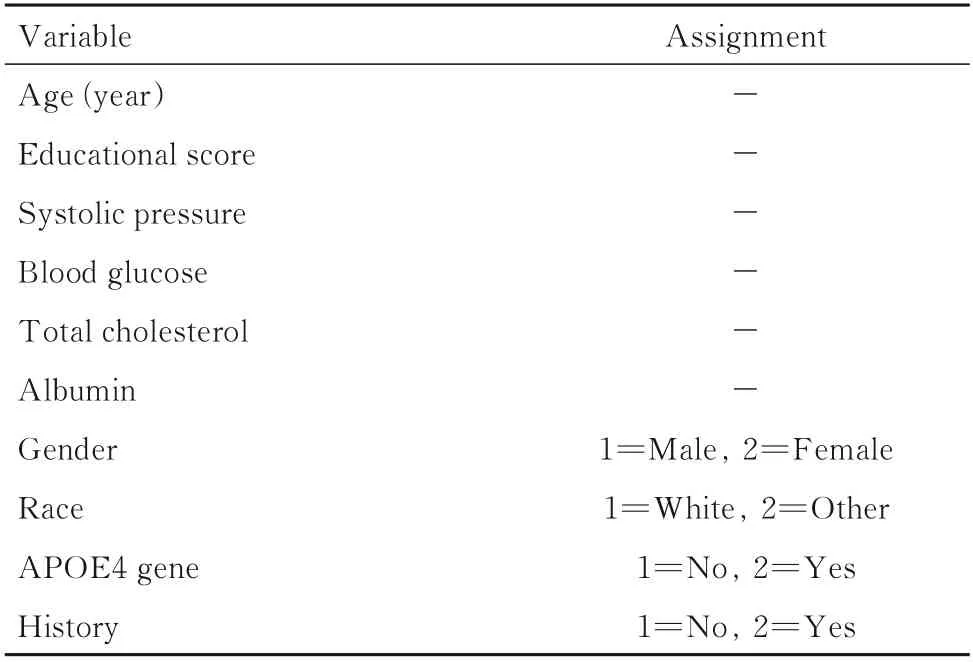
表2 纳入变量和赋值情况Tab.2 Included variables and assignments

2.3 425 名随访者纵向数据的分位数回归分析

采用贝叶斯线性分位数模型分析MMSE 不同分位数点的影响因素。根据MMSE 评分标准，当MMSE 的分位数分别取τ=0.15、τ=0.25 和τ=0.75 时，对应的评分分别为痴呆、认知障碍和正常的判断界值。因此，本研究选择在MMSE 评分的τ=0.15、τ=0.25、τ=0.75 和τ=0.85 时构 建分位数回归模型，结果见表3。在MMSE 评分的不同分位数上，白蛋白、血糖浓度、教育程度评分和APOE4 基因均为MSSE 评分变化的影响因素。在MMSE 评分的τ=0.15，τ=0.25 和τ=0.75 时，年龄成为MSSE 评分变化的影响因素；在MMSE 评分 的τ=0.15，τ=0.75 和τ=0.85 时，性 别 是MMSE 评分改变的影响因素；仅在τ=0.85 时，种族是MMSE 评分变化的影响因素。

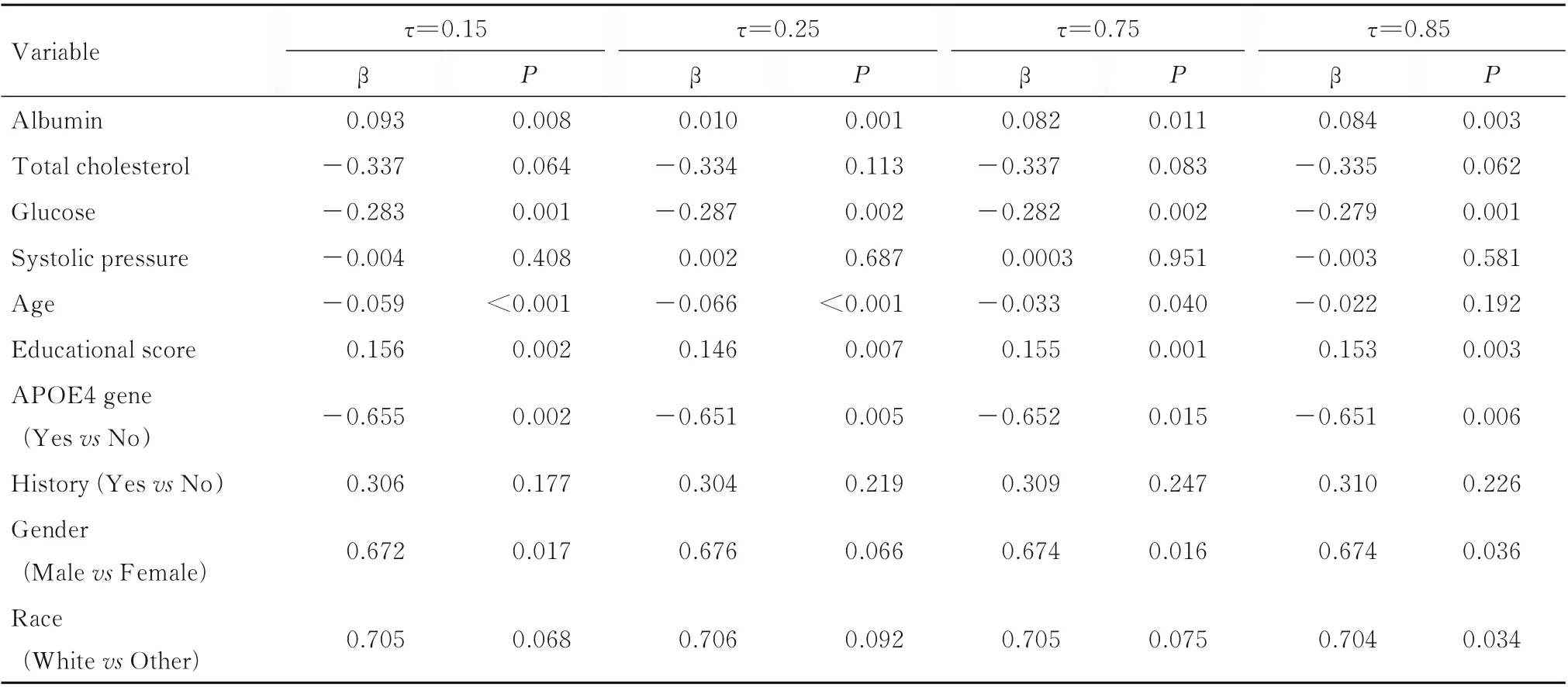
表3 425 名随访者纵向数据的贝叶斯线性分位数模型分析Tab.3 Bayesian linear quantile model analysis on longitudinal data of 425 interviewers

2.4 425 名随访者生存数据的Cox 回归分析本研究基于年龄、性别、教育程度评分、种族、婚姻情况、APOE4 基因、家族史、基线收缩压、基线血糖浓度、基线总胆固醇和基线白蛋白等变量构建影响AD 发病的Cox 比例风险模型。仅有APOE4基因对AD 发病有影响，存在APOE4 基因的人群发生 AD 的风险是无 APOE4 基因人群的2.174 倍。见表4。

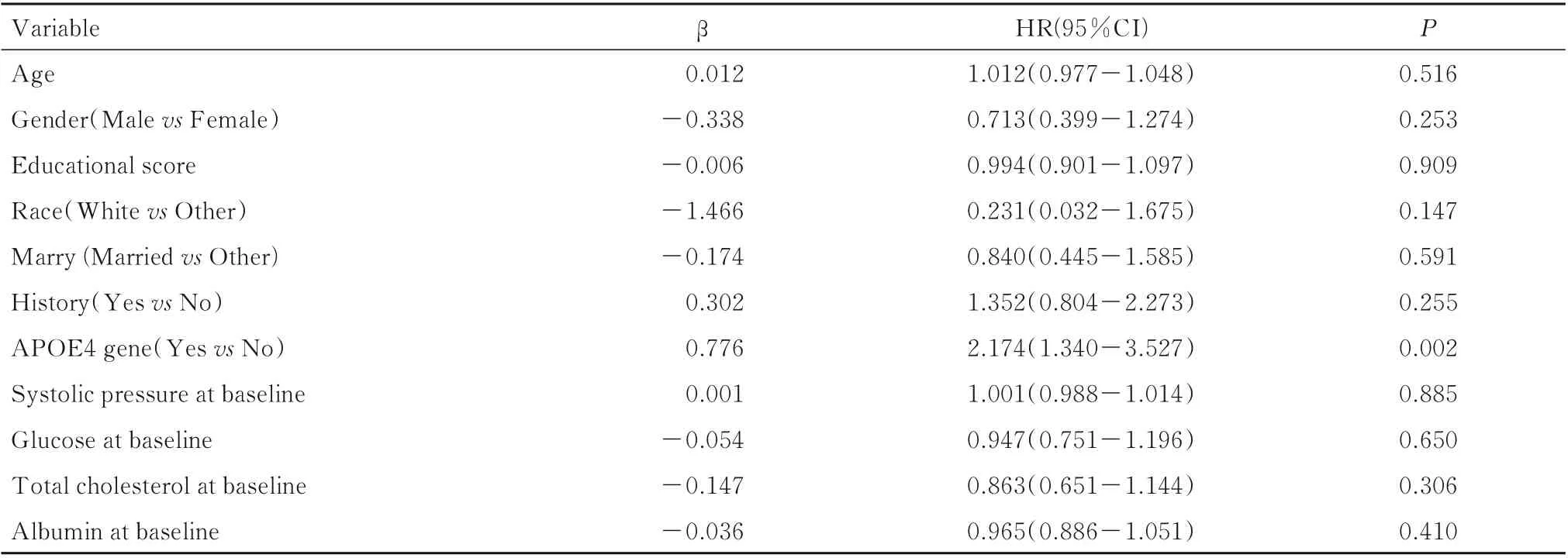
表4 425 名随访者的生存数据Cox 比例风险回归模型分析Tab.4 Cox proportional risk regression model analysis on survival data of 425 followers

2.5 425 名随访者的贝叶斯分位数回归联合模型分析本研究分别选择在MMSE 评分的τ=0.15、τ=0.25、τ=0.75 和τ=0.85 处，建立贝叶斯分位数回归联合模型。白蛋白、血糖浓度、年龄、APOE4 基因、性别和教育程度评分在不同分位数水平上均是MMSE 评分的影响因素。当MMSE 评分的τ=0.25 时，白蛋白和性别变量对MMSE 评分的影响最小，而变量APOE4 基因和教育程度评分在此分位数对其影响程度最大。即使是相同的影响因素，如血糖浓度，在不同百分位数对MMSE 评分的影响程度不同，在MMSE 评分的τ=0.15、τ=0.25、τ=0.75 和τ=0.85 时，血糖浓度每增加1 个单位，MMSE 分数分别降低0.327、0.175、0.212 和0.205，影响程度逐渐下降，年龄在不同分位数上呈现影响程度逐渐下降的趋势。联合模型生存子模型分析得到的结果与单Cox 模型结果不同，在考虑到MMSE 评分轨迹变化的情况下，除APOE4 基因变量外，种族在不同分位数上是影响AD 发病的风险因素，变量基线总胆固醇在MMSE评分的τ=0.25，τ=0.75 和τ=0.85 为AD 发病的风险因素，风险比分别为0.739［exp（－0.302），95%CI：0.624，0.882］、0.767［exp（－0.265），95%CI：0.629，0.938］和0.778［exp（－0.251），95%CI：0.669，0.909］。而家族史在MMSE 评分的τ=0.75 和τ=0.85 时是影响AD 发病的风险因素，风 险 比 是1.725 ［exp （0.545），95%CI：1.154，2.578］和1.251［exp（0.224），95%CI：1.093，1.487］。在MMSE 评 分 的τ=0.15、τ=0.25、τ=0.75 和τ=0.85 时，体内存在APOE4 基因的人群发生AD 的相对危险度是无APOE4 基因的2.188 倍（95%CI：1.775，2.620）、1.751 倍（95%CI：1.422，2.042）、1.706 倍（95%CI：1.391，2.102）和 2.056 倍 （95%CI：1.439，3.206）。见表5。

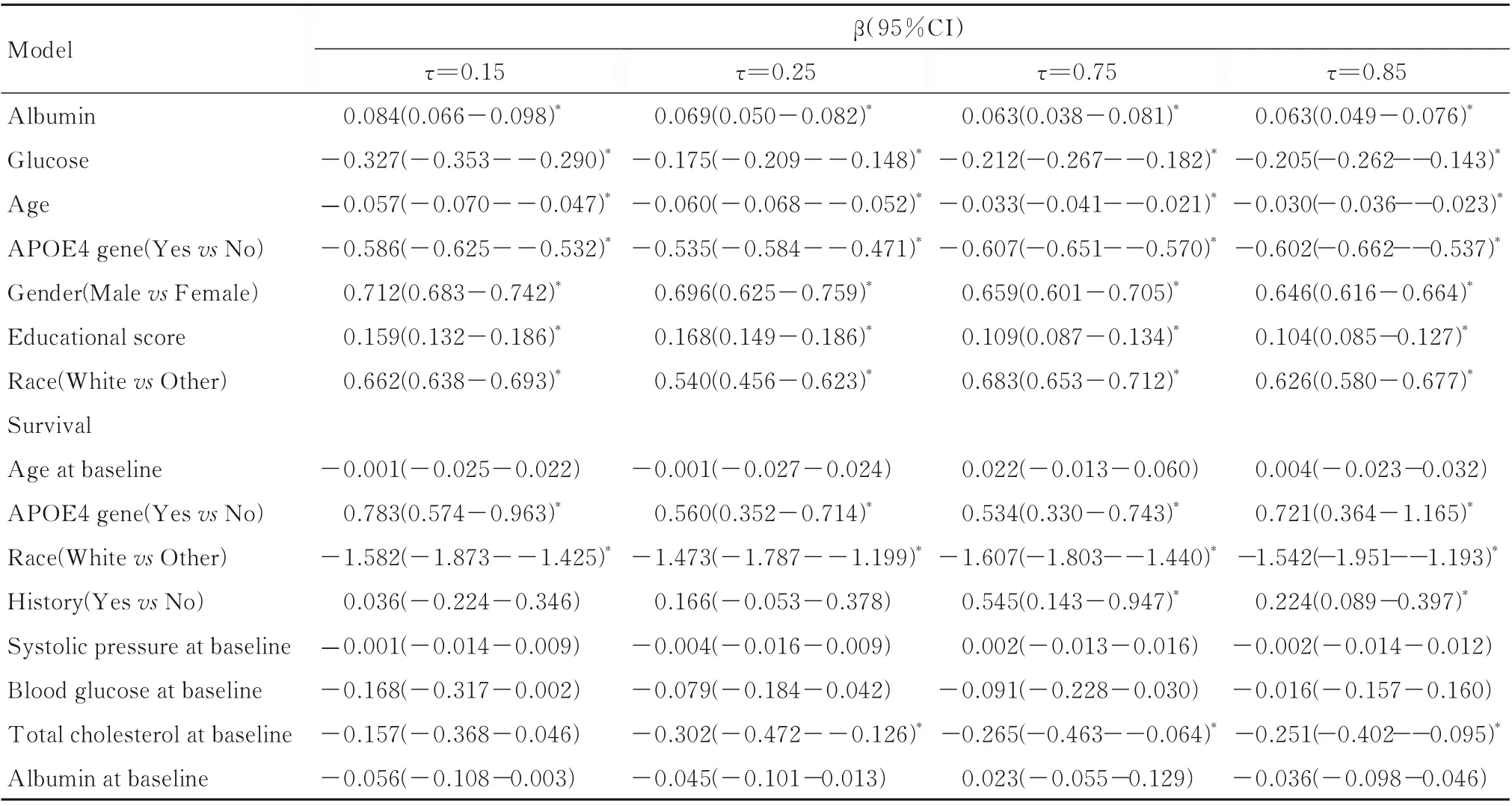
表5 425 名随访者的贝叶斯分位数回归联合模型的纵向子模型分析Tab.5 Longitudinal sub-model of bayesian quantile regression joint model analysis on 425 followers

3 讨 论

AD 是一种进行性中枢神经系统退行性疾病，是老年痴呆症的所有类型中最常见的一种［17-18］。然而AD 病因错综复杂，目前尚无有效的治疗方法。因此，探讨分析影响AD 发病的重要危险因素具有重要的临床意义。本研究采用贝叶斯分位数回归联合模型，对MMSE 评分不同分位数处的AD 的发病风险因素进行了深入探讨分析。

分位数回归模型结果显示：不同人群的MMSE 评分影响因素不同，白蛋白、血糖浓度、年龄、教育程度评分、性别、种族和APOE4 基因是MMSE 评分的主要影响因素。Cox 比例风险模型结果显示：仅有APOE4 基因对AD 的发病有影响，该结果与其他研究结果一致［19］。另有研究［20-21］结果显示：家族史和教育程度评分亦是AD发病的风险因素，造成本研究结果与其他国内外研究结果［20-21］不一致的原因可能是随访时间过长，左删失类型数据较多。通过贝叶斯分位数联合模型的纵向子模型分析结果显示：与单独的分位数回归模型结果相同，所有变量均是MMSE 评分的主要影响因素，不同分位数水平的MMSE 评分人群，影响因素不同。白蛋白对MMSE 评分的影响程度变化趋势呈现白蛋白随着MMSE 评分的升高，影响程度逐渐减小。贝叶斯分位数联合模型的生存子模型分析结果显示：APOE4 基因和种族是AD 发病的主要影响因素，基线总胆固醇仅在τ=0.15 时不是AD 发病的影响因素，而家族史在τ=0.75 和τ=0.85 时是AD 发病的影响因素，该研究结果与其 他 学 者 的 研 究 结 果 一 致［22-23］。YU 等［24］研 究 发现：高血压、肥胖和家族史也是AD 发病的危险因素，该研究结论与本研究结果不一致。

综上所述，白蛋白、血糖浓度、年龄、教育程度评分、性别、种族和APOE4 基因是MMSE 评分轨迹变化的主要影响因素，不同MMSE 评分人群发生AD 的影响因素存在一定差异。因此，在AD的诊疗过程中，针对不同MMSE 评分人群，应采取有针对性的干预措施，进而有效降低AD 的发病风险。本研究结果尚存在一定的局限性。如本研究中的研究变量较少，仅包含一些临床指标，未包括饮食习惯可纠正因素等［25］，因此，采取的干预措施受到一定的限制。另外，本研究仅对不同MMSE 评分轨迹变化状况下的AD 发病风险因素进行研究，后期在条件许可的情况下，可以考虑针对更多的生物标志物进行讨论，进而对AD 的发病风险因素进行进一步深入探讨。