引导学生探究解法,变式练习强化应用
2023-05-05广东省深圳市深圳科学高中518129朱小亮
广东省深圳市深圳科学高中(518129) 朱小亮
在最新高考评价体系中,作为学科素养指导体系,强调了“知识整合”,根据应对问题情境的需要,合理地组织相关知识和能力,注重发散性,提出新视角、新方法[1].因此对于一类经典问题,不应该浅尝辄止,而应当引导学生多角度,多方位分析,拓展学生的思维空间,提升学生的思维能力.
双变量问题灵活多变,综合性强,蕴含着丰富的解题技巧和思想方法,因此是高考的热点,也是难点.本文以一道双变量不等式问题解法教学为例,引导学生自主解法探究,并做了变式练习和应用,期待对学生的思维能力有所提升.
题目已知f(x)=xex−mx2,m∈R.若函数f(x)在(0,+∞)上有两个零点x1,x2,证明:x1+x2>2.
法一:差值换元
令xex−mx2=0,因为x>0,所以ex=mx,所以ex2=mx2,ex1=mx1,两式相除,得

评注这是答案给出的解析,令t=x2−x1,通过差值换元,把双变量问题转化为单变量问题,然后再构造函数,从而转化为证明单变量不等式.然而这道题解法丰富,教师不能就题讲题,浅尝辄止,而应引导学生探究更多解法,以提升学生思维能力.
法二:比值换元

评注法二用比值换元的方法,把双变量问题转化为单变量问题,然后再构造函数,从而转化为证明单变量不等式,这也是很重要的类比思想.在解题过程中,引导学生解题的方法有:1.取对数.2.对数分开走.

法三:对数均值不等式

评注法三,根据对数不等式,快速找到转化思路,运算更加简洁,但是要能构造出对数不等式的形式,有解题条件限制.
师问:以上三种方法均从条件的结构式子出发,经过整体换元或者结构变形进行转化,从而证明x1+x2>2.如果我们从结果x1+x2>2出发,用分析法找x1+x2>2成立的充分条件呢?
这个问题想引导学生向极值点偏移方向思考,但学生之前没有学过极值点偏移,学生一时没有思路,因此老师应做一些铺垫.
师问:f(x)=0有两个零点,可以转化为什么问题?
师问:我们再考察x1+x2>2,如果把x1移到右边,会出现什么结果?
学生开始自己探究,发现x1+x2>2,转化为x2>2−x1,而x2,2−x1都在极值点1的右边,在一个单调增区间上,从而证明x1+x2>2,可以转化为证明g(x2)>g(2−x1),又g(x1)=g(x2),又可以转化为证g(x1)>g(2−x1),从而转化为单变量问题,再构造对称函数F(x)=g(x)−g(2−x)证明,具体证明如下:
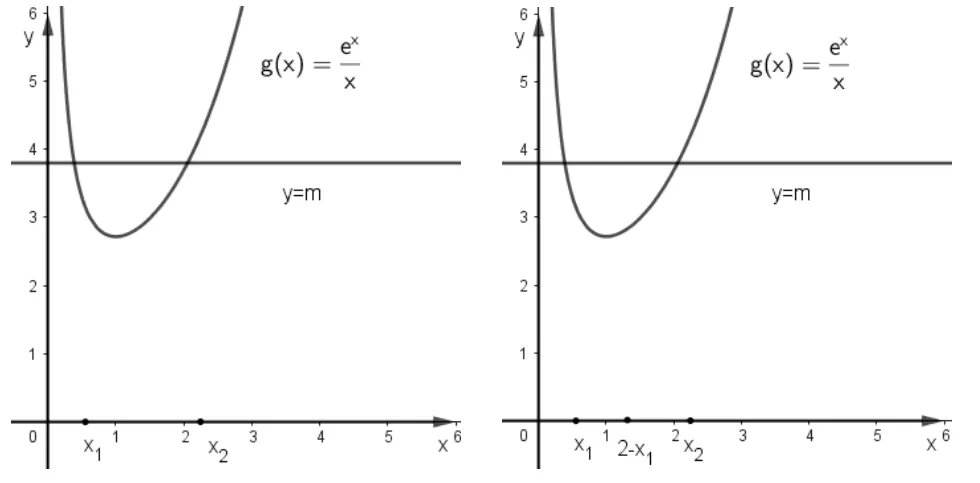
法四:极值点偏移
令f(x)=xex−mx2=0,因为x>0,所以ex=mx,得记x∈(0,1),g′(x)<0,g(x)递减,x∈(1,+∞),g′(x)>0,g(x)递增,g(1)=e,x→0+,g(x)→+∞,x→+∞,g(x)→+∞,所以m>e时,g(x)有两个零点x1,x2,且0
要证x1+x2>2,需证x2>2−x1,又g(x)在(1,+∞)上递增,所以等价证明g(x2)>g(2−x1),又g(x1)=g(x2),所以等价证明g(x1)>g(2−x1).记F(x)=g(x)−g(2−x)(0 记φ(x)=ex−ex(2−x)(0 师问:x1+x2>2,可以转化为>1,x=1是函数g(x)的极值点,如果函数图形关于x=1对称,那么应该有现在说明极值点相对向左偏移,这就是极值点偏移问题.大家回顾一下法四,总结一下极值点偏移问题题型和解答步骤. 学生开始自己探究总结,相互讨论补充,得到极值点偏移题型和解答步骤: 极值点偏移题型:若函数f(x)有极值点x=a,f(x)有两个零点x1,x2,且两个零点分布在极值点x=a两侧,证明:x1+x2>2a(或者x1+x2<2a). 极值点偏移题型解答步骤:(1)移项,将x1或者x2移到右边(一般移范围较小的),(2)转化,利用单调性,转化为函数值的不等式,(3)构造对称函数. 师问:法四涉及到指数运算和指数不等式放缩,计算量较大,那有什么方法可以优化运算呢? 于是有了下面法五. 令f(x)=xex−mx2=0,因为x>0,所以ex=mx,得易知m>0,两边取对数得lnm=x−lnx,记g(x)=x−lnx,g′(x)=1−x∈(0,1),g′(x)<0,g(x)递减,x∈(1,+∞),g′(x)>0,g(x)递增,g(1)=1,x→0+,g(x)→+∞,x→+∞,g(x)→+∞,所以lnm>1,即m>e时,g(x)有两个零点x1,x2,且0 要证x1+x2>2,需证x2>2−x1,又g(x)在(1,+∞)上递增,所以等价证明g(x2)>g(2−x1),又g(x1)=g(x2),所以等价证明g(x1)>g(2−x1).记F(x)=g(x)−g(2−x)(0 评注法四,法五,都是极值点偏移,构造对称函数.但法五两边取对数后,对称函数的导函数形式较简单,运算量比法四少很多,指对互化,也是解题的常用技巧. 以上对一道例题进行了5种解法,总结了处理双变量问题的一些策略.当然遇到具体例题,还要根据例题的结构特点,选择恰当的方法,例如以下的变式练习: 变式一已知f(x)=xex−mx2,m∈R.若函数f(x)在(0,+∞)上有两个零点x1,x2,x1 学生都能想到差值换元和比值换元,但用比值换元,采用对数分开走的技巧,运算量较少.解答过程如下: 变式二已知f(x)=xex−mx2,m∈R.若函数f(x)在(0,+∞)上有两个零点x1,x2,x1 学生通过解法对比,选择极值点偏移方法解答,但法四的极值点偏移解答,会涉及到复杂的指数运算,所以选择法五,取对数之后,再用极值点偏移解答. 解析如图, 总结一道经典题,就是一个宝藏,蕴含着丰富的研究价值.本道题蕴含的解题技巧:整体换元,指对互换,对数分开走,构造对称函数,参数分离,指数不等式放缩等;蕴含的思想方法:数形结合,类比思想,等价转化,包括:通过差值换元或者比值换元,把两元问题转化为一元问题;将函数的零点问题转为两个函数交点问题;将指数问题转化为对数问题;将自变量大小问题转化为函数值大小问题.培养了学生综合分析,数学运算的能力. 教师应当经常带领学生挖掘经典题,以问题为驱动,由点到面,由浅入深,循序渐进引导学生深度思考,自主探究,同时可以变式练习,加深对解题方法的理解和应用,从而促进学生思维发展,提升学生的分析能力.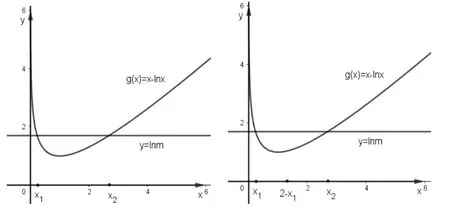
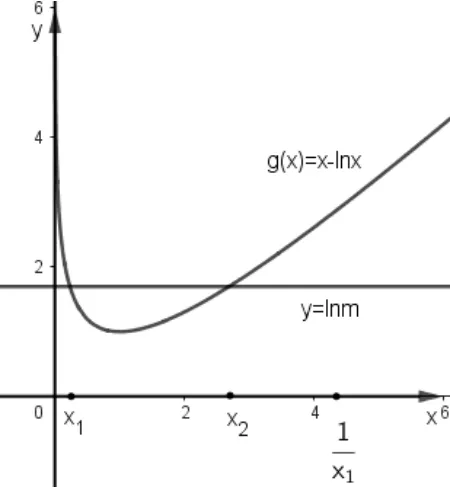
法五:两边取对数,极值点偏移