点代法求解圆锥曲线中一类定点问题

广东省佛山市第一中学(528000) 刘振兴

圆锥曲线中动直线过定点问题是高考的热点问题,对学生数学抽象、逻辑推理、数学建模、数学运算、直观想象等数学核心素养的要求较高,是区分学生数学学科思维水平的有力载体.其中有一类定点问题出现频率很高,就是由圆锥曲线上两个动点确定的直线过定点问题,本文对这类定点问题进行探究,给出了一个新的解答视角.

1 引理和性质

引理1已知两点A(x1,y1),B(x2,y2),则直线AB的方程为(y2−y1)x+(x1−x2)y+x2y1−x1y2=0.

推论1若A(x1,y1),B(x2,y2)两点都在抛物线y2=2px(p>0)上,则直线AB的方程为2px−(y1+y2)y+y1y2=0.

证明由=2px1,=2px2,结合引理1得2px−(y1+y2)y+y1y2=0.

2 方法应用

2.1 点代法在双曲线中的应用

例1(2022年佛山市高三教学质检卷第21题)已知双曲线C的渐近线方程为且过点

(1)求C的方程;

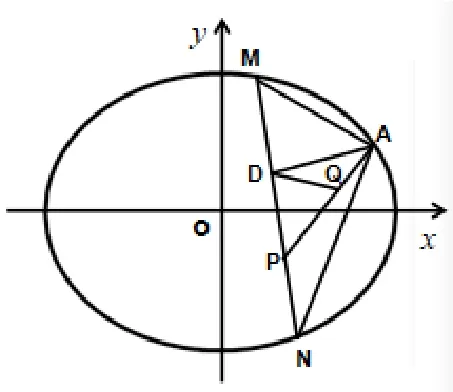
(2)设Q(1,0),直线x=t(t∈R)不经过P点且与C相交于A,B两点,若直线BQ与C交于另一点D,求证:直线AD过定点.

解(1)=1(过程略).

(2)设A(x1,y1),D(x2,y2),则B(x1,−y1).由引理1知,直线AD的方程

根据性质2得

联立 ①②得x1y2−x2y1=3(y2−y1).代入(*)式得(y2−y1)(x−3)+(x1−x2)y=0,所以直线AD过定点(3,0).

评析利用B,Q,D三点共线, ①式出现x1y2和x2y1项,结合引理1和性质2,解答过程非常简洁,运算量降低很多.

2.2 点代法在椭圆中的应用

例2(2022年深圳市高三第二次调研考试第21题)已知椭圆=1(a>b>0)经过点且焦距|F1F2|=线段AB,CD分别是它的长轴和短轴.

(Ⅰ)求椭圆E的方程;

(Ⅱ)若N(s,t)是平面上的动点,从下面两个条件中任选一个,证明:直线PQ经过定点.

(2)t=2,s∈R,直线NC,ND与椭圆E的另一交点分别为P,Q.

解(Ⅰ)=1(过程略).

(Ⅱ)若选(1),由题意A(−2,0),B(2,0),设P(x1,y1),Q(x2,y2).由引理1知,直线PQ的方程

又由性质1得

若选(2),求解方法类似,过程略.

评析利用A,N,P和B,N,Q都是三点共线,消去t后 ①式出现3x2y1和x1y2项,结合性质1求解,解答高效.

2.3 点代法在抛物线中的应用

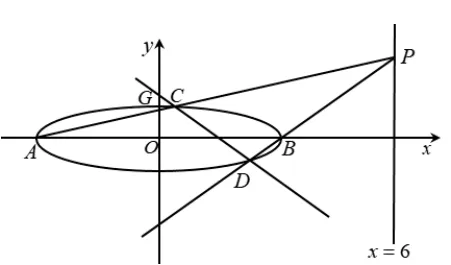
例3(2022年湘潭市三模考试第21题)已知抛物线E:y2=2px(0

(1)求抛物线E的方程;

(2)设点P(x0,y0)在抛物线E上,且4,过P作圆C:(x−4)2+y2=4的两条切线,分别与抛物线E交于点M,N(M,N两点均异于P).证明:直线MN经过R(6,−y0).

证明(1)y2=2x(过程略).

(2)设M(x1,y1),N(x2,y2),由推论1得直线PM方程为2x−(y0+y1)y+y0y1=0.直线MN的方程为

评析利用推论1,需求出y1+y2和y1y2,故只要找出y1和y2对应的一元二次方程就可以完成求解.

3 高考链接

例4(2020年新高考山东卷第22题)已知椭圆=1(a>b>0)的离心率为且过点A(2,1).

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足．证明:存在定点Q,使得|DQ|为定值.

解(1)=1(过程略).

(2)设M(x1,y1),N(x2,y2).由引理1知,直线MN的方程为

1○−②化简得3(x2y1−x1y2)=2(y1−y2)+(x1−x2).代入(*)式得所以直线MN过定点

当直线AM和AN的斜率为零或不存在时,不妨设直线AM的斜率为零,直线AN的斜率不存在.由A(2,1),得M(−2,1),N(2,−1),所以直线MN方程为x+2y=0,此时直线MN也过点

例5(2020年高考全国Ⅰ卷理科第20题)已知A,B分别为椭圆1(a>1)的左、右顶点,G为E的上顶点,=8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明:直线CD过定点.

解(1)E:=1(过程略).

(2)由题意A(−3,0),B(3,0),设C(x1,y1),D(x2,y2),P(6,t),由引理1知,直线CD的方程为

又由性质1得

4、总结

从以上例题可以看出,用点代法求解圆锥曲线中动直线过定点问题,过程简洁,解答高效.但要注意只能是圆锥曲线上两动点(x1,y1)和(x2,y2)确定的直线过定点问题,才能用点代法求解.解题时,经常利用到三点共线或斜率关系等条件,通过代数变形,转化出x2y1和x1y2项,然后结合引理1及其性质求解.