一道压轴题的命制与思考

安徽省合肥市合肥一六八玫瑰园学校东校区(230601) 蔡志永 汪文龙

作为初中数学教师,笔者有幸参加了2022年安徽省某高中高一入学选拔测试试卷的命制.对于如何选择命题材料、控制试题难度、确定考查内容等有了切身体会.现与大家分享与探讨,不妥之处敬请批评指正.

1 命题立意

根据本次测试的性质,学校命题组要求,本次试卷考查的内容、方法和数学思想等都是初中阶段所学,不涉及高中特别是高一的知识和解题技巧.防止部分学生暑假提前学习,无法保证公平性.同时,又需要考查出高中阶段对学生所需的部分能力.

基于以上要求,考虑到初高中在知识方法等方面的衔接、本题在整张试卷的地位,数学命题组决定以二次函数为载体.二次函数的图形与性质是初中的重点也是难点,它与一元二次方程、韦达定理、因式分解以及简单的一元二次不等式等都有密切联系.同时,二次函数还可以提供平面直角坐标系的解题环境,进而与两点间距离公式关联.

为了考查高中阶段所需的部分能力,命题组决定加入三角形和圆的知识,特别是三角形的外接圆和内切圆等知识,通过数形结合的思想,考查学生的计算能力.为步入高中以后,学习数列和解析几何等内容做好准备.同时增加题目的难度,提高区分度.

2 命制过程

初稿1若n为正整数,二次函数y=x2−nx+1的图像与x,y轴分别交于点A(x1,0),B(x2,0)、P三点,如图所示.记∆PAB的外接圆半径为Rn.

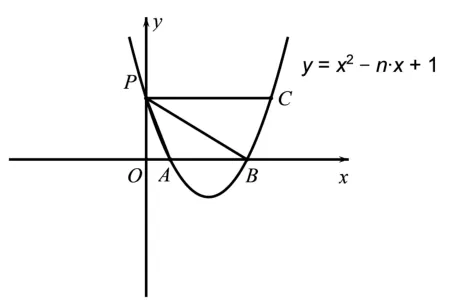
(1)求n的最小值;

(2)求Rn;

此题以二次函数为背景,以图像与坐标轴的三个交点为顶点构造三角形,借助平面直角坐标系,重点考查了二次函数与一元二次方程的联系,简单二次不等式的解法,三角形外接圆的性质,两点间距离公式等知识.侧重考查学生的逻辑思维能力和运算能力.

但此题考查高中数列知识的“味道”太浓,特别是第(3)问还考查了数列放缩、裂项等处理技巧.不能有效考查学生的现有水平,与命题立意相悖.于是命题组重新考虑,将第(3)问删掉,在保留(1)(2)的前提下,加入∆PAB的内切圆,完成初稿2.

初稿2若n为正整数,二次函数y=x2−nx+1的图像与x,y轴分别交于点A(x1,0),B(x2,0)、P三点,如图所示(图形不变).记∆PAB的外接圆半径为Rn.

(1)求n的最小值;

(2)求Rn;

(3)求∆PAB的内切圆半径rn.

1.发展经济，尽可能地满足人民群众的物质生活需要。生产力的发展是解决民生问题的前提条件。抗战时期人民生活异常困苦，在改善民生问题上，毛泽东更为关注的是物质生活的关照方面。他说：“要不要民生呢？使老百姓有点饭吃有点衣穿。”［2］125改善民生，“一句话，使人人有衣穿，有饭吃，有书读，有事做”［2］133；民生问题，“只有从切切实实的有效的经济发展上才能解决”［4］892；组织人民发展生产，“就是我们党的根本路线，根本政策”［5］468。

此题在初稿1的基础上,减少数列技巧的考查.通过求解三角形内切圆的半径,增加了运算的复杂性.对学生的计算能力和方法有了更高的要求,为高中解析几何等内容的运算作准备.除此之外,本题还考查了三角形的内切圆的性质、韦达定理、分母有理化、因式分解、约分以及整体代入等知识和技能.

但此题第(3)问与第(1)(2)问之间联系不大,且与初中知识联系也不紧密.数学思想的考查又过于单一.如果作为压轴题的话,不仅难度不够,三个小题的难度梯度设置也不合理.因此,为了增加初中知识的考查和数学思想的渗透,提高压轴题的考查区分度,命题组参考近几年安徽中考关于二次函数的考查方式,对初稿1和初稿2的试题结构及设问重新调整、构思与优化,最终定稿如下:

定稿若n为正整数,二次函数y=x2−nx+1的图像与x,y轴分别交于点A(x1,0),B(x2,0)、P三点.过点P作x轴的平行线,交二次函数图像于点C,如图所示.记∆PAB的外接圆和内切圆半径分别为R、r.

(1)求P、C两点的坐标(可以用含n的式子表示)及n的最小值;

(2)(i)求证:PA2+PB2=PC2

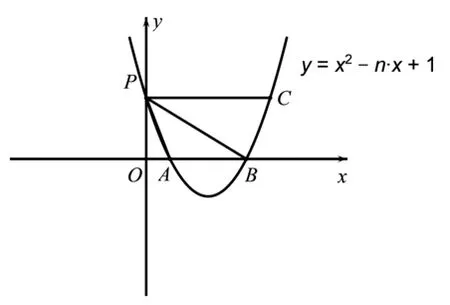
(ii)求∆PAB的外接圆半径R;

解(1)当x=0时,y=1,∴P(0,1);∵PC//x轴,∴点C的纵坐标为1,当y=1时,x2−nx+1=1,解得x1=0,x2=n,∴C(n,1);∵二次函数图像与x轴交于不同的两点,∴一元二次方程x2−nx+1=0的判别式∆>0,即n2−4>0,解得n>2或n<−2,∵n为正整数,∴n的最小值为3.

此题在初稿1和初稿2的基础上,将部分问题进一步优化.其中第(1)问增加了求P、C两点坐标,一方面是降低题目的着手点,让该题的难度梯度设置的更合理;另一方面也可以帮助学生熟悉题目背景.该问还考查了二次函数的图形与性质,一元二次方程的解,二次函数与一元二次方程的联系以及解简单的一元二次不等式.不管是从难度上还是知识方法上,都为后面做了铺垫.第(2)(i)问是命题组成员在研究了PA,PB,PC三条线段之间的数量关系以后新增加的.三者除了满足PA2+PB2=PC2这一关系之外,还满足PA·PB=PC.但由于平方的关系学生更熟悉,能减轻做题时的畏难情绪,同时平方的形式也更能引导学生采用两点之间距离公式,进而利用韦达定理以及一元二次方程根的意义化简求解.这一计算技巧的渗透也为第(3)问打下了基础,体现了解题方法考查的连续性.第(2)(ii)在前两稿的基础上将Rn改为R,目的是为了弱化高中的表达方式,让学生在更熟悉的表述中做题,以此提高做题正确率.本小问考查了三角形外接圆的性质、两点间距离公式,一元二次方程根的意义.同时,在求解过程中,考查了学生的计算能力.最后一问除了考查以上知识和技能,三角形内切圆,还着重考查了学生函数思想、换元思想的运用.利用一些计算技巧和换元变化,将转化为二次函数表达式,然后利用二次函数的性质求出的最大值.可以说,该题相较于前面两题,考查的方式学生更熟悉,考查的知识和技能更全面,同时还渗透了数形结合、换元以及函数等数学思想.

3 命题感悟

通过该题的命制,笔者对于命制一道压轴题时,命题材料的选择、考查内容的确定、试题难度的控制有了更多的思考和感悟.

3.1 命题材料的选择

初中阶段涉及的知识点很多,但适合作为压轴题素材的内容不多.一般具有以下三个特点的内容较适合作为压轴题素材:一是重点知识;二是与其他知识联系点多;三是要服务于考试目的.

所谓重点知识,主要是指学生在数学学习过程中占据重要位置的内容,同时也是课标和教材强调的重点知识.比如二次函数,在初高中函数思想的渗透中都占据着极其重要的位置,同时二次函数的学习也为学生以后学习其他高等函数在方法和知识上都打下了基础.

与其他知识联系点多,这一特点保证了考查知识和方法的灵活性,同时便于控制题目的效度和区分度.与二次函数有关的联系点有:一元二次方程、一元二次不等式、因式分解、韦达定理、配方法、整体思想、函数思想;由于坐标系的存在,为几何知识的考查提供了背景,因此又与两点间距离公式、三角形的面积和周长、三角形的内心与外心等相联系,在考查计算的同时,又渗透了数形结合思想和换元思想.而这些联系点,将极大的方便命题者根据考查目的设置更合理的考查方式,同时也有利于控制考查难度,提高试题区分度.

一张试卷,特别是压轴题,考试目的是首先要满足的,也是这份试卷的意义所在.本次考试要求考查的内容、方法和数学思想等都是初中阶段所学,同时又需要考查出高中阶段对学生所需的部分能力.二次函数作为初高中都极其重要的知识,自然很容易达成考试目标.

3.2 考查内容的确定

压轴题,作为一份试卷的灵魂,要特别重视数学最核心的“四基”:基本知识、基本技能、基本思想方法和基本活动经验,而数学基本思想方法的考查更是数学的本质所在.本题考查了与二次函数相关的众多知识点、运算能力,同时还渗透了函数思想、数形结合思想、整体思想、换元思想等,较为全面的考查了学生的综合水平.

3.3 试题难度的控制

一道题目难度过高或过低都较容易达成,但如何通过难度的控制达到区分的效果就不那么简单了.这其中问题的呈现方式和问题串之间的衔接至关重要.

问题的呈现方式包含两个方面:问题串的设置和整道题目特别是每个小问题的表述方式.问题串的设置一般按照难度从低到高的方式,第一问突破口要宽,难度要低,主要帮助学生熟悉题意;后面几问的难度依次增加,但跨度不宜过大.题目的表述方式也会影响学生的思考.题目中字词的使用如果符合学生的习惯,便于学生理解,学生做起来也将更顺畅,无形中也会降低题目的难度.

本题第一问主要是让学生熟悉题目,通过求点P和点C,引导学生通过分析函数图形与x轴交点情况求解n的最小值.第(2)(i)通过学生较熟悉的线段平方和的形式,引导学生利用两点间距离公式、韦达定理、整体代换等知识和方法求解,难度中等.同时也是为后面两问的求解提供计算方法的指引.而最后一问的换元思想则提高了对学生的要求,难度很大.本题虽然考查的角度不是初中生所熟悉的,但整道题目的表述都避免了高中的习惯,比较符合初中生的理解习惯.