基于SOLO分类理论的中考数学试题的比较研究<br/>——以2020—2022年连云港市数学中考试卷为例

基于SOLO分类理论的中考数学试题的比较研究
——以2020—2022年连云港市数学中考试卷为例

2023-05-05江苏省连云港市新海初级中学222000姜晓刚

中学数学研究(广东) 2023年4期

江苏省连云港市新海初级中学(222000) 姜晓刚

《义务教育数学课程标准(2022版)》指出:“遵循课标要求,严格依标命题.全面理解和体现课程标准要求,依据课程标准所规定的课程目标、内容要求、学业要求和学业质量命题,各领域考查内容所占比例与其在课程标准中所占比例大体一致,难易程度大体平衡,保证命题的科学性.”

本文将基于SOLO分类理论,从考查的领域主题和SOLO层次的视角分析研究2020年、2021年和2022年的连云港市数学中考试卷,旨在剖析连云港市中考数学试卷结构和命题趋势,为课堂教学、中考复习提供有价值的参考和借鉴.

1 研究对象

选取2020—2022年连云港市中考数学试卷及评分标准为研究对象.以下将2020—2022年这三套中考试卷分别简称为“20年卷”,“21年卷”,“22年卷”.

2 研究工具

以比格斯(Biggs)和卡利斯(Collis)在其代表作《评价学习的质量—SOL0分类法》(1982年)中系统阐述的SOLO分类理论为研究工具.

3 试题领域主题的划分

《义务教育数学课程标准(2022版)》指出:“义务教育阶段数学课程内容由数与代数、图形与几何、统计与概率、综合与实践四个学习领域组成.”其中“数与代数”分为“数与式”、“方程与不等式”、“函数”等三个主题;“图形与几何”分为“图形的性质”、“图形的变化”、“图形与坐标”等三个主题;“统计与概率”分为“抽样与数据分析”、“随机事件的概率”等两个主题.

4 试题的SOLO层次划分

依据SOLO分类理论将中考试题分为单点结构(U)试题、多点结构(M)试题、关联结构(R)试题和抽象拓展结构(E)试题,分别对应简记为U试题、M试题、R试题、E试题.

5 试题SOLO层次评定

在试题考查内容领域主题、SOLO层次划分确定后,请三位资深老师(专家)独立地将三年的连云港市数学中考试卷的每道试题进行主题归类和SOLO层次评定,然后再对于不同评定结论的试题展开面对面的研讨,以致形成共识.

特别说明:(1)由于“综合与实践”领域的特殊性,所有试题按照前三个领域主题进行归类;(2)如果一道试题考查的知识点涉及了几个领域时,以重点考查的知识点为依据归类;(3)大题的各小问所考查知识点领域不同,将把各小问按(2)分别分类(其分值也对应处理);(4)如果试题SOLO层次处于多点结构和关联结构之间、关联结构和抽象拓展结构之间的情况时,将从学生对试题的熟悉程度、解题过程的复杂程度、解题所需的思维水平的高低等方面进行分析,最终确定试题的SOLO层次.

6 “领域主题+SOLO层次”数据分析

按照试题的SOLO层次划分,分别对2020年、2021年、2022年的连云港市数学中考试题进行归类和评定,得到如下数据表1:

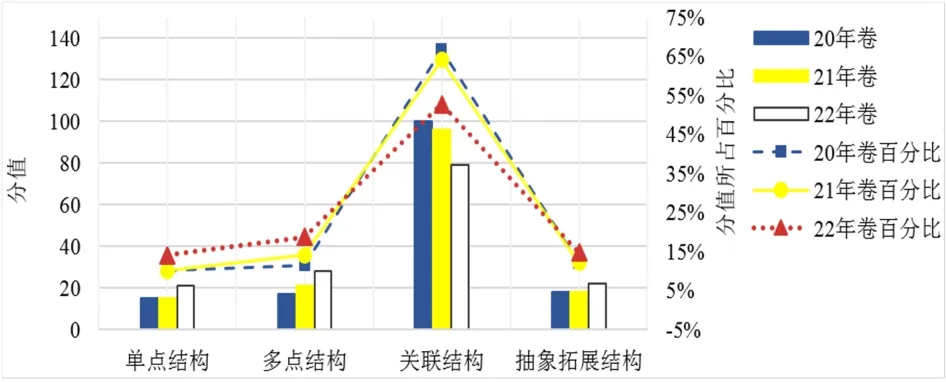
图1

从SOLO结构层次比重对照表对比可以看出:

(1)2022年试卷中的单点结构(U)试题简单题(即简单题)与多点结构(M)试题较简单题(即较简单题)所占比分别为14%、18.67%,大于2021年的10%、14%和2020年的10%、11.33%,说明2022年的试卷更加注重考查考生的数学基础知识、基本技能、基本思想和基本活动经验.

(2)2020年试卷中的关联结构(R)试题(即中档题)的比重为66.67%,稍高于2021年试卷的64%,高于2022年试卷的52.67%,说明2020年的试卷偏向于考生应该具备的数学思想、数学方法和数学活动经验的考查.

(3)2020年试卷、2021年试卷、2022年试卷的抽象拓展结构(E)试题(即难题)所占比重分别为12%、12%、14.66%,相差无几,说明三份试卷对考查考生较高的分析问题、解决问题的能力的定性与定量几乎是一致的.

(4)为了计算整份试卷的难度,笔者参照了苑宝立在《用SOLO分类评价理论评价吉林中考试卷》一文中对SOLO层次题目的赋值方法:单点结构层次(U层次)题目赋值为1分,多点结构层次(M层次)题目赋值为2分,关联结构层次(R层次)题目赋值为3分,拓展抽象结构(E层次)题目赋值为4分,则试题的难度为:U的比重*1+M的比重*2+R的比重*3+E的比重*4.经过计算,2020年试卷、2021年试卷、2022年试卷的难度分别为2.81、2.78、2.68,难度以2022年试卷为略低.三份试卷在难度的把握上还是几乎保持稳定的.

按照试题考查的领域主题和SOLO层次划分,分别对2020年、2021年、2022年的连云港市数学中考试题进行归类和评定,得到数据表2:

从考查主题的SOLO结构层次比重表对比可以看出:

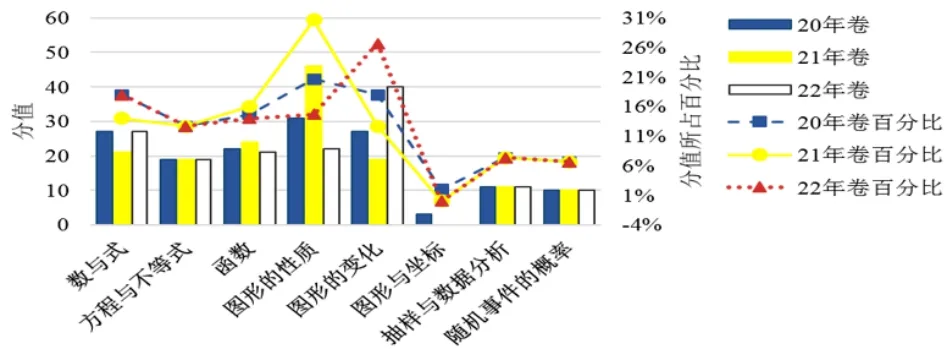
图2

(1)三份试卷在抽样与数据分析主题与随机事件的概率主题几乎没有差别,延续了统计与概率领域的命题的质量与规律.

(2)在数与代数领域内,三份试卷对方程与不等式主题的考查几乎没有变化,2021年试卷在数与式主题的考查比重小些、在函数主题的考查比重略大些.2020年试卷与2022年试卷在数与代数领域内的考查几乎是一致的.

(3)在图形与几何领域内的波动就大了些.2022年试卷偏重于图形的变化主题的考查,2021年的试卷更加注重对图形的性质主题的考查,三份试卷缺乏对图形与坐标主题的足量的考查.

按照试题考查的领域主题和SOLO层次划分,分别对2020年、2021年、2022年的连云港市数学中考试题进行归类和评定,得到如下数据表3:

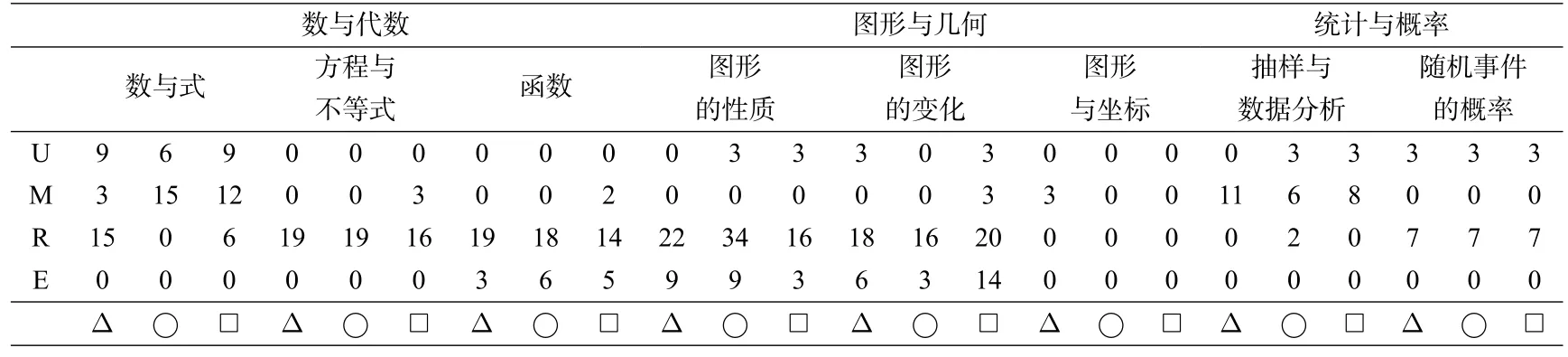
表1

从考查主题的SOLO结构层次分值表对比可以看出:

(1)三年试卷的单点结构(U)试题(简单题)和多点结构(M)试题(即较简单题)多以“数与式”主题的内容为主,其次是“抽样与数据分析”主题.

(2)三年试卷的关联结构(R)试题(即中档题)多以“方程与不等式”、“函数”、“图形的性质”、“图形的变化”主题的内容为主.

(3)三年试卷几乎都缺乏对“图形与坐标”主题的考查.

(4)三年试卷对“随机事件的概率”主题的考查的题型和SOLO结构层次几乎没有变化.

(5)“函数”、“图形的性质”和“图形的变化”主题是抽象拓展结构(E)试题(即难题)考查的重点.其中2022年试卷“图形的变化”的“E试题”的分值达到14分之多.

7 建议

7.1 重视关联结构(R)试题

关联结构(R)试题一题包含多个知识点,可以帮助学生构建系统的知识体系,培养学生分析、总结与知识迁移能力.关联结构(R)试题在难度上表现为中档题,符合数学中考以中等难度试题为主的命题要求.教学、复习中应重视重视关联结构(R)试题,命制模拟试卷时应保证足量的关联结构(R)试题.

7.2 注重试题的SOLO层次结构分布的均衡

对于各领域主题的SOLO层次分布进行分析时,发现三年的连云港市数学中考试卷都存在部分主题的SOLO层次缺失,如“图形与坐标”几乎整体缺失、“随机事件的概率”等主题也存在部分缺失.在命制试卷时,应注重SOLO层次分布的全面性,低思维层次的试题考查尽量涵盖各个主题,并尽力合理增加高思维层次试题在更多主题的分布.