数学史融入数学概念教学的实践探索与启示

广东省深圳市深圳大学附属实验中学(518000) 王金莹

《普通高中数学课程标准(2020修订版)》中的课程基本理念提出“体现数学的文化价值”.数学课程应适当反映数学的历史、应用和发展趋势,数学的社会需求,数学发展和社会发展相互推动的作用,数学科学的思想体系,数学的美学价值,数学家的创新精神.数学课程应帮助学生了解数学在人类文明发展中的作用,逐步形成正确的数学观,实现学科渗透“五育并举”,将素养教育落实到课堂中.

本文以对数的概念和弧度制的概念这两个教学片段为例,展示数学史融入数学概念教学的实践探索,并从中得到启示.

1 教学片段1:对数的概念

1.1 环节(1):问题引入,以史启迪

数学史1(“对数思想”的源起):

15世纪的数学家对一列有序的正整数思考过这样的问题.例如下表:

0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 4 8 16 32 64 128 256 512 1024 2048 4096

1544年史提非在《整数算术》中把第一行数称之为“指数”,德文中意为“代表者”,后来成为正式的数学术语.欲求第二行任意两个数的积,只要计算与这两个数对应的第一行的数之和即可.如求32×128,32对应的第一行数是5,128对应7,5+7=12,在12下面的4096就是所求的数.

问题1第一行的数和第二行的数存在什么关系?

追问:若想知道4096是2的多少次方,即已知底数和幂,应该如何求指数?

师生活动:教师通过介绍数学史上数学家对表格中对应数的计算思考,引导学生发现其中的关系,从已知底数和指数求幂的问题,转化到思考已知底数和幂,如何求指数的问题上来.

设计意图:问题1其实就是“对数思想”的源起,由第一行的和对应求第二行的积,其实是指数的运算法则,反之,想要由第二行的积求第一行的和,则要利用对数的运算法则,其中蕴含了指数与对数的相互转化,从而引入对数的概念,也为下一课时学习对数的运算做好铺垫.

1.2 环节(2):指对互化,深化概念

问题2:如果ax=N(a>0,a1),那么x=?

对数的概念:x=logaN,其中a称为底数,N称为真数,读作以a为底N的对数.

追问:对数和指数存在怎样的对应关系?如何进行对数与指数的相互转化?

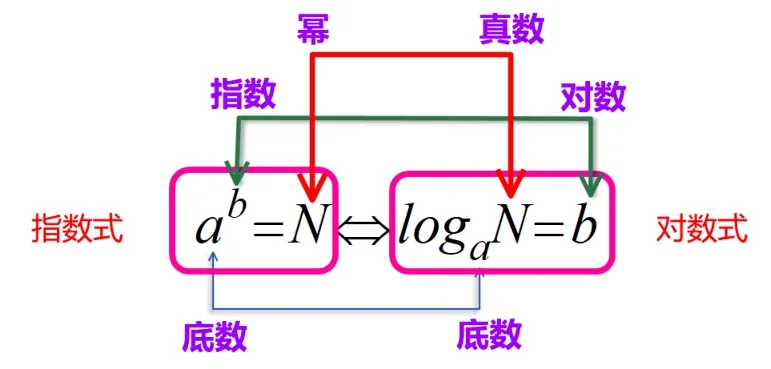
图1 指数式与对数式的关系

数学史2(改编自课本128-129页阅读与思考“对数的发明”):

【创始人】苏格兰数学家纳皮尔于1614年出版了《奇妙的对数定律说明书》,标志着对数的诞生.纳皮尔借助运动学,用几何术语阐述了对数方法,定义x为y的对数:其中,e为自然对数的底.

纳皮尔在讨论对数概念时,并没有使用指数与对数的互逆关系,因为当时还没有明确的指数概念,直到20多年后的1637年法国数学家笛卡尔才开始使用指数符号,18世纪瑞士数学家欧拉才发现指数与对数的互逆关系,他指出:“对数源于指数”,而对数的发明先于指数,这成为数学史上的珍闻.

【自然对数】伦敦数学家斯彼德于1619年以e为底制得《新对数表》.

自然对数logeN=lnN表示以自然对数e为底的对数,其中e≈2.71828.

【改良与补足】英格兰数学家布里格斯1624年出版《对数算术》,建议改为以10为底的常用对数,并制得1至20000以及90000到100000的14位以10为底的对数表;到1628年由佛拉哥进一步补足.

常用对数log10N=lgN表示以10为底的对数.

【在中国的发展】波兰数学家穆尼阁于1648年(清顺治3年)到访中国,于1653年与中国薛凤祚合编《比例对数表》,这是我国最早的对数著作.清代数学家戴煦发现多种求对数的便捷方法,并发表著作《求表捷术》,包含《对数简法》(1845)、《续对数简法》(1846)、《假数测圆》(1852).

问题3根据指数与对数的转化,由写出纳皮尔对数x与自然对数的关系.

师生活动:教师说明指数式中的底数、指数、幂分别一一对应对数式中的底数、对数、真数,并列举几个简单指数式转化为对数式的例子.进而介绍对数的发明历史,引出自然对数和常用对数的概念,学生通过问题3巩固练习如何进行指数与对数的转化,得到纳皮尔对数

设计意图:介绍对数的发明与发展的数学史,一方面是为了让学生感受知识的发生发展过程,理解所学知识是为了解决什么问题,同时感受中国数学家在相关知识中的建树,在数学学习中培养民族自豪感;另一方面也很顺畅地引入了自然对数、常用对数的概念.最后通过纳皮尔对数与自然对数的关系,让学生巩固练习指数与对数的转化.

2 教学片段2:弧度制

2.1 环节(1):问题引入,激发兴趣

引导语:在初中我们学习过锐角三角函数,但是存在一个问题,自变量的值与函数值不能运算,阻碍了三角函数通过运算法则形成其他初等函数.

问题1若s=30◦,t=sin30◦,则s+t=?

追问:如何解决s=30◦与t=sin30◦之间不能相加的矛盾?

师生活动:学生小组讨论思考问题,教师在学生提出因为“单位不同”而不能相加的原因之后,引导学生考虑用sin30◦的度量单位——长度来度量30◦,以实现单位的统一.从而确定本节解决问题的突破口:用长度度量角度.

设计意图:通过用角度作为自变量表示三角函数使得自变量的值与函数值不能进行运算的问题引入,让学生产生认知冲突,从而激发探究的兴趣.

2.2 环节(2):以史启迪,类比探究

问题2如何用长度度量角度呢?

追问:类比角度制中的定义,如何引入一个利用长度来度量角的新单位制?

数学史1(1◦的来源):

1◦的定义最早是由古巴比伦人提出的,当时人们信赖“地心说”,认为地球是圆的.由于地球的公转,地球上的我们就像看走马灯一样,在特定的时间看到特定的星座.古人发现了这个规律,并且以星座为参照物,近似观察出循环周期为360天,也就是一年.因此,天就被等分成了360份,也就是圆被等分成了360份.因而在“把一个圆周的角度固定为360◦”的前提下,给出了的定义:把圆周长划分成360份,每一份弧长所对应的圆心角定义为1◦的角.类比1◦的定义得到新单位定义:把圆周长划分成几份,每一份弧长所对应的圆心角是1个单位的角.

问题3用什么来划分圆周长?

师生活动:教师通过介绍数学史,与学生共同类比1◦的定义给出新单位定义的范式,引导学生回想突破口:用长度度量角度.进而想到可以利用圆中与长度相关的量.

追问3-1在圆中,我们学习过哪些与长度相关的概念?

追问3-2用哪一个长度的量来划分圆周长?

师生活动:教师通过不变性引导学生想到用半径划分是合理的.在一个定圆中,弦长、弧长会随着圆心角的变化而变化,但半径是不变的.

追问3-3以半径为单位划分圆周长,则圆周长会被划分成几份?

追问3-4你能完成“弧度定义:把圆周长划分成____份,每一份弧长所对应的圆心角是____(1个单位)的角”了吗?

师生活动:学生根据以上探究得出答案“把圆周长划分成2π份,每一份弧长所对应的圆心角是1弧度的角”.

设计意图:问题2属于对突破口的进一步分析,通过数学史的介绍引出1◦的定义,进而类比1◦的定义,经历4个追问的探究建立起弧度的定义.学生在这个过程中经历了概念的建构与“发现问题、提出问题、分析问题”的过程,体会“类比”的数学思想方法.

活动1几何画板动态探究

拖动点A改变半径(∠AOB的大小不变),观察弧长AB与半径OA比值的变化.

追问3-5弧长AB与半径OA比值与半径有关吗?

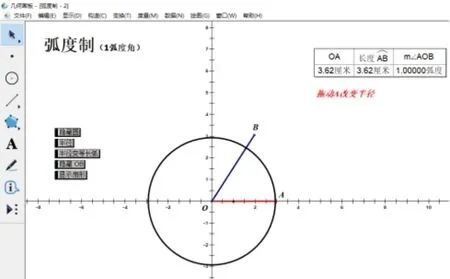
图2 探究弧长与半径的比值与半径的关系

师生活动:教师通过动态展示半径的变化过程.学生通过观察到弧长AB与半径OA比值始终不变,发现弧长AB与半径OA比值与半径无关,也就是说,这个比值随α的确定而唯一确定.教师在此基础上进一步给出精确的弧度定义.

设计意图:通过活动1认识到用等于半径的弧所对的圆心角作为弧度制的度量单位的合理性.

2.3 环节(3):深化概念,角弧互化

活动2根据弧度的定义完成表格.

问题4角α的弧度数的正负由什么决定?

追问:在一个半径为r的圆上,圆心角α对应的弧长为l,那么角α的弧度数的绝对值是多少?

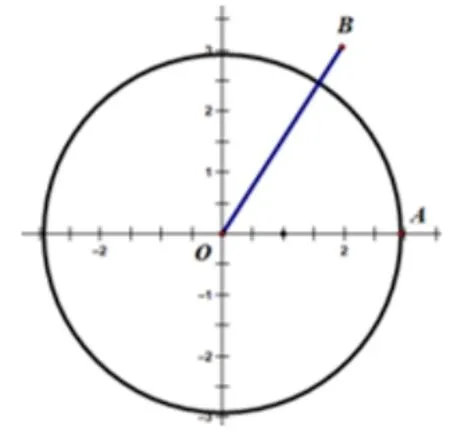
图3

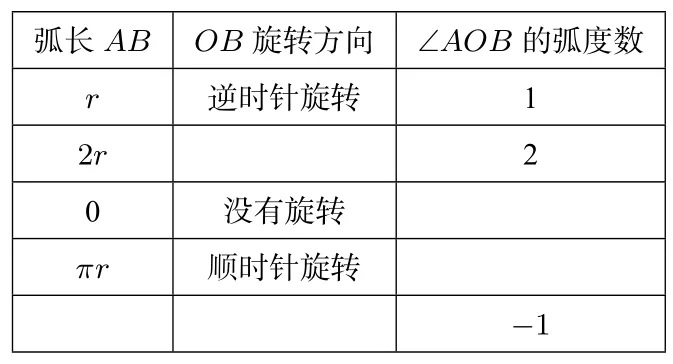
弧长AB OB旋转方向∠AOB的弧度数r 逆时针旋转1 2r 2 0没有旋转πr 顺时针旋转−1

设计意图:通过完成活动2,学生可以归纳出规律:角的终边的旋转方向决定了角的弧度数的正负;且结合定义知道

数学史2(弧度的来源):

【萌芽】弧度制是从圆周运动的角度来定义的.古人的世界观是“天圆地方”,人们的旅行都被视为直线运动.可事实是,地球是圆的,随着技术的发展,大航海时代的来临,大家都越来越认识到这一点,传统意义上的直线,在地球表面都不复存在,必须重新定义球面距离的含义.弧度制也是在这样的背景下开始萌发.

【发展】公元6世纪,印度人在制作正弦表时,曾用同一单位度量半径和圆周,孕育着最早的弧度制概念.

【提出】1748年瑞士数学家欧拉在他的一部划时代著作《无穷小分析概论》中的第八章提出了弧度制思想——把圆的半径作为弧长的度量单位.这一思想将线段与弧的度量统一起来,大大简化了三角公式及计算.

【诞生】19世纪北爱尔兰数学教师汤姆生正式使用了“弧度(radian)”一词,是半径(radius)与角(angle)两词的合成,被人们广泛接受和应用.

设计意图:此环节是对弧度制本质的深化,通过数学史的介绍,让学生感受一个数学概念从萌芽到诞生的曲折过程,感受数学的人文精神,体会到引入弧度制的价值.

问题5如何进行角度与弧度的相互换算?

师生活动:教师引导学生从一个圆周的弧度数与角度数进行分析,学生独立思考解决问题.

思考:在弧度制下,角的集合与实数集之间存在怎样的关系?

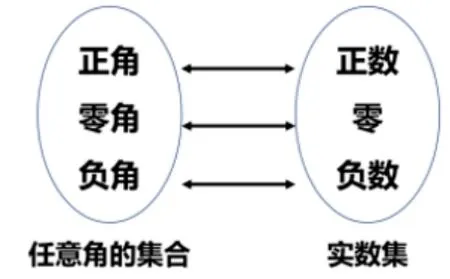
图4 任意角的集合与实数集的关系

设计意图:通过问题5与活动2完成教学目标:掌握角度制与弧度制的互换,知道一些特殊角的弧度知道弧度制下的角的集合可以与实数集建立一一对应关系.

3 数学史融入数学概念教学的实践启示

3.1 以数学文化搭建脚手架,发挥学生自主性

研读新教材、新课标可以发现,数学文化是激发学生学习兴趣、联系数学与现实世界与其它数学内容的重要工具,例如教学中可以提供体现数学发生发展过程的数学史,提出宏观的研究思路,由具体的例子引导学生提出微观想法.

从现实世界的数学化、数学发展与社会发展的相互推动过程、数学历史出发,呈现问题情境,以数学的联系、数学的价值、数学的发生发展过程搭建学习架构,设计逻辑连贯的学习内容、环环相扣的问题串、系列化的数学活动,促使学生自主发现和提出问题、分析问题和解决问题.

3.2 联系已有知识经验,充分调动数学认知结构

为了引导学生建构良好的数学认知结构,对教材中数学文化拓展、数学史介绍的阅读材料进行再创造和补充,一方面,教师要熟悉学生原有的认知结构,即我们常说的“备学生”,把握学习内容的上下位关系,把握数学的整体性,根据学生已有的知识经验,找到学生思维的生长点.另一方面,要创设合理的问题情境,以问题调动认知结构的整合或是造成认知冲突,驱动思维发展.总而言之,就是要让学生看到材料有兴趣,有想法,有表达欲和求知欲.

3.3 注重研究数学对象的基本路径

研究一个数学对象的基本路径包括:(1)明确研究对象,即定义、表示、分类;(2)明确研究对象的性质、特例及与其它内容的联系.对于性质,可以开展定性研究和定量研究.通过数学史中介绍数学对象发明和发展的过程,我们要关注到研究一个新的数学对象的基本路径,这样有助于学生在之后的学习中举一反三,类比迁移到其它问题中去.例如通过介绍数学史上1◦的来源,类比1◦的发现和定义的过程来定义新的度量角的制度.再如通过回顾数学史上的数系扩充过程,我们为解决生产、生活、数学情境中遇到的问题而定义了负数、有理数、无理数……,进而为解决方程x2+1=0在实数集上没有解的问题,继续将实数集扩充到复数集.