采用滑动窗口与克里金插值算法的复杂系统可靠性评估方法
2023-05-05叶爽怡扈晓翔司小胜袁勃
叶爽怡,扈晓翔,司小胜,袁勃
(1. 西北工业大学自动化学院,710129,西安; 2. 火箭军工程大学导弹工程学院,710025,西安;3. 西安微电子技术研究所,710065,西安)
复杂系统在运行过程中,一旦出现故障不仅会造成经济损失,更甚者还可能造成人员伤亡。因此,在复杂系统的大规模使用中,及时对其进行可靠性评估并采取一定的预防维修措施,对于切实保障复杂系统的运行安全性具有重要的意义[1]。
可靠性是指产品在规定时间规定条件完成规定功能的能力[2],此产品可以是一个部件也可以是一整个系统,而产品的质量可以通过可靠性进行衡量。因此,复杂系统的可靠性评估可以提高产品的质量和使用年限,提高市场竞争力,满足现代生产的需要和人们生活的需求,还可以节约成本并获得巨大的经济效益。随着技术的不断进步和发展,系统也在日益朝着大型化、复杂化、智能化的方向发展,正是由于其迅速发展,才更容易受到外界因素的影响[3-4]。这类系统在受到外界环境、材料疲劳特性以及结构性能老化等因素的影响时,随着其使用,部件的性能就会发生不可避免地持续性退化,最终导致整个系统失效,而失效不可避免地就会带来大量的经济损失,甚至严重的还有可能造成安全事故的发生[5-8]。为了减少经济损失以及避免事故的发生,对复杂系统在完全失效之前的可靠性评估就十分重要。
针对上述问题,周国辉等[9]以WSN实际监测数据为研究对象,提出了基于证据推理规则的WSN数据可靠性评估模型。Li等[10]通过建立有限元模型模拟车辆轨道动力学,从车轨系统运行角度对板式轨道结构进行可靠性评估。由于工业过程中对可靠性和安全性的需求不断增加,Huang等[11]提出了将自抗扰控制应用于含扰动系统的早期故障诊断中。姜涛[12]针对多状态系统运行过程中的状态观测数据的多层次性以及系统状态的退化行为,建立了基于动态贝叶斯网络的多状态系统可靠性评估模型。Huang等[13]针对滚动轴承早期故障特征隐蔽以及难以识别的缺点,提出了变分模态分解和随机配置网络相结合对滚动轴承可靠性评估以及早期故障诊断。陈保家等[14]提出了一种基于比例协变量模型和Logistic回归模型混合的可靠性评估方法。胡伟飞等[15]针对液体火箭发动机运行过程中外界载荷及自身属性存在不确定性导致失效的问题,提出了一种基于泰森多边形区域划分结合自适应克里金代理模型的液体火箭发动机可靠性分析方法。Liang等[16]介绍了一种基于马尔可夫状态模型的简化方法用于复杂安全系统可靠性评估。赵福均等[17]基于证据推理对大型系统的安全性评估提出了一种在线监测和评估的方法,满足了系统对于实时性的要求,但在对历史、当前和未来时刻的安全性状态进行融合时,假设3个时刻的安全性状态重要性一致。实际情况下,根据Kriging(克里金)的思想,越靠近当前时刻权重越大,因此本文提出一种采用滑动窗与克里金插值算法的复杂系统可靠性评估方法,目的在于改进三时刻安全性状态重要性一致的问题。
本文方法首先借助滑动窗口技术不断更新下一时刻的状态,剔除历史时刻的状态[18],以便达到对滑动窗口内数据动态更新的效果。接着,根据Kriging的思想,按照越靠近当前时刻权重越大的思想[19],对安全性状态的权重进行重新自适应调整。最终,基于证据推理算法融合自适应调整后的权重及其置信分布完成对整个系统的在线可靠性评估。
1 可靠性评估模型与问题描述
1.1 可靠性评估模型
对于传统的可靠性评估和分析方法大多采取离线的分析方式。对于大多数的实际复杂系统,实时的反映系统的可靠性评估结果对系统的长期运行是大有裨益的。然而,要想建立一个精确的可靠性评估模型,在现实中是很难实现的。复杂系统的可靠性评估可以通过影响系统状态正常运行的指标来反映,因此借助传感器监测数据来反映系统的运行状态。对一个复杂系统进行可靠性评估时,综合考虑历史、当前和未来时刻的安全性状态信息,可以得到更加全面的结果。与赵福均等[17]研究的大型系统在线评估方法不同,本文的模型不考虑未来时刻的状态信息,因为未来时刻包含太多的不确定性信息,因此只需要综合考虑历史时刻和当前时刻的安全性状态信息。但是,历史数据的数量选择又是一个亟待解决的问题,所以本文借助滑动窗口技术,提前确定好最优滑动窗口的大小,随着时间的推移,每次更新一个时刻,剔除一个历史时刻,这样不断地更新滑动窗口内的数据,以便对权重及其置信分布进行动态更新。对于滑动窗口内状态的权重分配问题,基于越靠近当前时刻权重越大的思想,对滑动窗口内的状态权重进行自适应调整,这样调整后的结果更加切合实际。本文的主要内容如下:首先,借助滑动窗口技术确定最优滑动窗口的大小,更新下一时刻的状态,剔除历史时刻的状态;接着,根据Kriging的思想,越靠近当前时刻状态权重越大,对安全性状态的权重进行重新自适应调整;最后,使用证据推理算法对自适应调整后的状态权重及其置信分布进行融合,得到复杂系统整体的可靠性评估结果。
1.2 问题描述
根据上述可靠性评估模型的构建,存在以下两个问题需要解决。
问题1复杂系统是一个随时间变化的动态过程,历史和当前时刻的安全性状态信息权重需要在不同时刻不断地动态更新,而滑动窗口可以解决状态信息权重在线更新的问题。但是,滑动窗口大小的确定又是一个亟需解决的问题,因此问题1主要是解决滑动窗口数量选择的问题。
问题2为了全面综合考虑复杂系统的可靠性评估,需要将历史时刻的状态信息与当前时刻的状态信息进行融合。但是,在综合分析时又会引入一个新的问题,即靠近当前时刻的状态信息与远离当前时刻的状态信息对系统整体的影响应该如何界定。
根据Kriging的思想,按照越靠近当前时刻权重越大的思想对所有的状态信息的权重进行重新自适应调整,因此问题2主要是建立表达式
(1)
2 证据推理基础知识
对复杂系统进行可靠性分析时,早期使用较多的是传统的可靠性分析方法,如故障树、事件树等,但这些方法已经不足以解决复杂系统的可靠性问题。由于样本信息的缺失或不可靠,会导致某些确定性变量趋向于不确定。在这种情况下,传统的可靠性分析方法受到了约束和限制。证据理论算法对这样的不确定性分析方法具有独特的优势[20],可以利用变量所处的边界条件对不确定性的变量进行描述,这是概率模型所不能满足的。
但是,由于证据理论的不足,它对于完全冲突的证据、证据之间有关系、组合爆炸问题以及各个变量之间的重要程度和可靠程度无法解决,于是又引入了证据推理算法[21]。
证据推理算法表述如下。假设一个评估方案由L条证据进行分析评估,这L条证据ei(i=1,2,…,L)彼此之间是相互独立的,辨识框架定义为Θ,它是由N个不同的评估等级Fn(n=1,2,…,N)所组成的,Fn可以取Θ中的任意一个元素,因此Θ={F1,F2,…,FN}。这L条证据可以表示为置信分布形式ei={(Fn,βn,i),n=1,2,…,N;(X,βX,i)},也就是在ei(i=1,2,…,L)这条证据的支持下把这个方案评估为Fn这个等级的置信度是βn,i。Wang等[21]推导出了证据推理算法的解析算式
(2)
(3)
3 基于滑动窗与克里金插值算法的复杂系统可靠性评估
3.1 历史当前和未来三状态权重均分方法
赵福均等[17]的基于证据推理的动态系统安全性在线评估方法,已经详细地阐述了如何借助证据推理算法对复杂系统进行在线评估。为了得到更加全面的评估结果,首先需要预测未来时刻的指标信息,接着求取指标信息的动态权重,然后使用证据推理算法对指标信息融合得到安全性状态的信息,最后再利用证据推理算法融合安全性状态的信息得到整体安全性评估结果。然而,再次使用证据推理算法时,需要得到每一时刻安全性状态的相对权重信息,但现有的复杂系统可靠性评估中都是假设历史、当前、未来时刻安全性状态的重要性一致,通过均分权重融合安全性状态的置信分布得到整体的安全性评估结果。
这样做存在两方面问题:一方面,需要预测未来时刻的指标信息,但是未来时刻的信息包含太多的不确定性因素,会对最终的分析造成一定的阻碍;另一方面,单纯假设历史、当前、未来时刻安全性状态的重要性一致会造成历史时刻权重过大的问题,因为根据Kriging的思想,越靠近当前时刻权重越大,这就与假设的条件相矛盾。基于这两方面存在的问题,本文做出如下改进:①不考虑未来时刻的信息,只综合考虑历史和当前时刻安全性状态的信息,对整个系统进行可靠性评估;②基于滑动窗与克里金插值算法对状态权重进行动态更新以及自适应调整,最终得到整体的可靠性评估结果。
3.2 滑动窗口模型
滑动窗口是指数据流上的一个区间,窗口中保存着数据流中最新进来的T个数据,随着数据流上新的数据的到来,窗口队列不断更新第T+1数据进入,同时丢弃最早的一个数据。采用先进先出机制,保障窗口中总有T个数据,称为窗口队列。窗口队列数据是不断更新的,因此称为滑动窗口[22]。简而言之,就是用一组固定长度的窗口从长序列的起点滑到终点,每向前滑动一步,就剔除一个历史时刻,获取一个新的时刻,直至当前时刻为最终时刻[23]。借助此想法,本文采用固定窗口大小的滑动窗口,假定所有的安全性指标融合后的状态信息X有n个按照时间排列的数据集,其时间序列构造为X(n)=[x(1),x(2),x(3),…,x(k),…,x(n)],x(k)代表状态信息X的第k个时刻的数据。若以k为当前时刻,则指标信息融合后的安全性状态的前T时刻的时间序列可表示为X(k)=[x(k-T+1),…,x(k-1),x(k)],其中T为滑动窗口的大小。时间序列的滑动窗口如图1 所示。

图1 时间序列的滑动窗口Fig.1 A sliding window for time series
借助此想法,本文采用固定窗口大小的滑动窗口。固定窗口大小的确定根据Imani等[24]提出的多窗口查找器,其基本思想是任何给定的窗口大小的移动平均误差都会随着接近时间序列的实际窗口大小而减小,并随着越来越远离时间序列的实际窗口大小而增加,正确的窗口大小是移动平均值与平均值的距离最小的窗口大小。
目前,窗口大小的确定是由时间序列所反映的特点以及领域专家的意见来获取,结果包含人们的主观意见,可靠度会降低。因此,根据Imani等[24]的思想,首先根据安全性指标融合后的状态信息的时间序列X(n)=[x(1),x(2),x(3),…,x(k),…,x(n)],用一个窗口大小可变的时间窗口对此时间序列进行滑动平均。假设可变化的时间窗口为w,根据滑动平均的思想,新序列可以表示为
Y={y1,y2,…,yi,…,yn-w+1}
(4)
Y中的每一个新数据yi是根据窗口大小w滑动平均得到的结果,yi的具体计算公式为
(5)
式中x(i)表示初始时间序列的数据信息,i=1,2,…,n-w+1。
以上思想基于的假设条件是:对于一个最优的时间窗口大小T,根据T的滑动平均产生的新的序列Y与其平均值E(Y)之间的距离总和是最小的。
因此,根据上述思想,将可变的窗口大小w从最小值取到状态信息数量的最大值,对原始的序列计算不同窗口大小wj的滑动平均结果Yj,并计算新序列的平均值E(Yj),得到新序列与其平均值距离的总和sum(Yj-E(Yj))。将距离的总和作为纵坐标,时间窗口大小作为横坐标,绘制曲线图。曲线图中第一个局部最小值点对应的横坐标即为最优的时间窗口。
3.3 基于滑动窗与克里金插值算法的权重自适应调整策略
根据上述的滑动窗口模型,首先得到最优的滑动窗口大小,综合考虑多个历史和当前时刻安全性状态的信息,对复杂系统的可靠性进行评估。然而,针对滑动窗口内状态信息的相对重要性问题,考虑到克里金插值算法,靠近当前时刻的状态相对于其他时刻来说更重要。在进行融合时,一般更加注重离当前时间点近的时刻数据的重要性,而离当前时间点比较远的数据可以作为一种参考。
克里金插值的思想是利用已经存在的数据的加权求和来估计预测未知的数据,即在随机场中利用未观测到的值附近的值(已知值)去插值一个未观测到的值[19]。

(6)
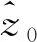
采取普通克里金方法求取权重,做出如下假设:
(1)数学期望未知,但是空间中任何一点的数学期望都是相同的,即E[z(x,y)]=μ;
(2)协方差函数cij未知,但是可以利用变异函数rij代替,因为rij(x,y)=E[(zi-zj)2]。
假设空间中任意一点的期望是相同的,而且空间的属性是均一的。因此,可以把每一个数值都记作是均值和一个随机偏差的加和,即z(x,y)=μ+R(x,y),通常方差可以被记为
σ2=var(z(x,y))=E[(z(x,y)-μ)2]
(7)
根据式(5),随机偏差的方差也是一个常数
var(R(x,y))=E[R2(x,y)]=σ2
(8)
(9)
(10)
(11)
在这里,定义半方差公式是rij=σ2-Cij,它的等价条件是rij=0.5E[(zi-zj)2],利用zi-zj=ri-rj可以很容易证明上述两个公式是等价的。
最终的目标是求出来一组最合适的权重系数使方差的估计值和实际观测值的方差最小,这就是求取权重系数的条件,即
(12)
将式(6)代入式(12),可以得到
(13)
又根据式(11)的条件以及定义的半方差公式,式(13)变为
(14)
根据式(11)的条件,式(14)变成了一个有条件的极值问题。选取拉格朗日乘数法进行求解,设参数为φ,构造的拉格朗日函数为
(15)
将式(14)代入式(15)后,为了使J最小,最终得到系数
(16)
根据克里金插值的思想,式(16)最终得到的系数便是每一个已知的观测值相对于未知点的权重系数,即权重自适应调整策略后得到的权重结果,表示为
ωi=λi,i=1,2,…,n
(17)
3.4 基于权重自适应调整策略的可靠性评估方法
首先,使用基于效用的信息转化技术得到输入指标信息的置信分布[25],利用ER算法对指标信息进行融合得到安全性状态的置信分布。然后,借助滑动窗口模型得到所需要的置信分布数据,再利用滑动窗与克里金插值算法对滑动窗口内的权重进行自适应调整。最后,利用ER算法将滑动窗口内数据的置信分布以及对应的权重进行融合,得到系统整体的可靠性评估结果。其中,置信分布表示融合后被划分的等级及相应等级对应的置信度。利用式(2)、(3)得到复杂系统整体的可靠性分析结果
O(R(k))={(Fl,β′l(k))},l=1,2,…,N
(18)
式中:Fl是N个评价等级;β′l(k)表示安全性状态融合之后的复杂系统整体被评估为Fl这个等级的置信度,置信度表示相信复杂系统此时被评估为相应等级的程度。将滑动窗口内自适应调整策略下的权重信息和指标融合后的置信分布进行融合,最终得到复杂系统整体的可靠性分析和评估的结果。
4 仿真结果与分析
为了验证本文所提方法的有效性,选取轴承作为研究对象,对上述方法进行仿真分析和验证。数据来源于西安交通大学机械工程学院雷亚国教授团队和浙江长兴昇阳科技有限公司历时两年的滚动轴承加速寿命实验[26]。实验选取的轴承为LDK UER204滚动轴承,本文在转速为2 100 r/min、径向力为12 kN的工况下选取Bearing 1_1数据集[26],针对其水平方向和竖直方向的数据进行融合。
将本文所提方法与假设历史、当前和未来时刻安全性状态同等重要的方法进行对比,得到的置信分布如图2和图3所示。
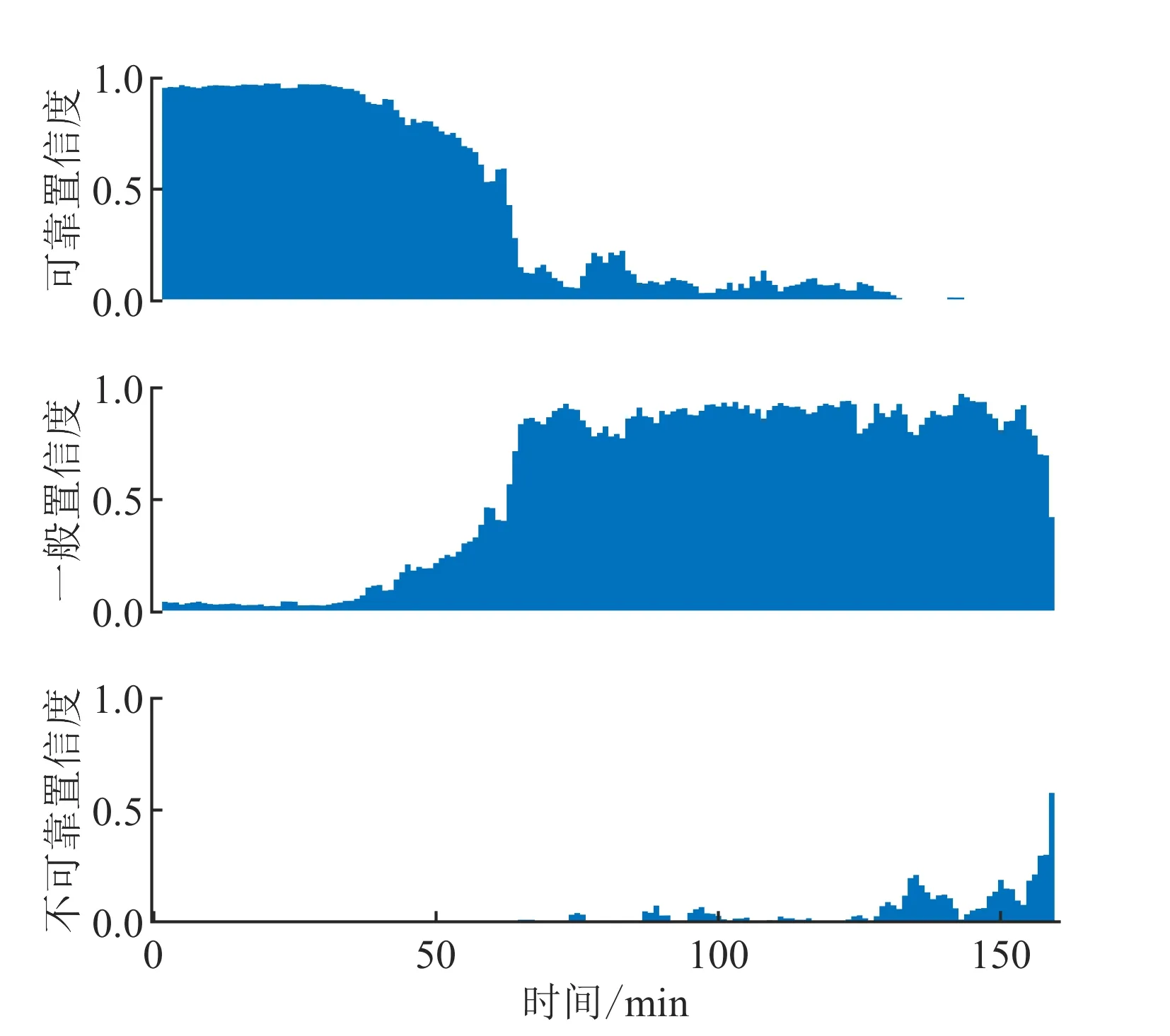
图2 三状态融合的置信分布Fig.2 Confidence distribution for three-state fusion
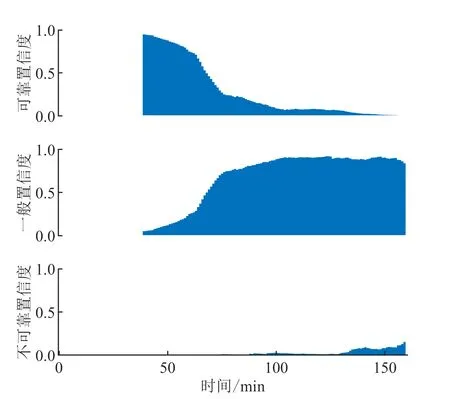
图3 滑动窗口状态融合的置信分布Fig.3 The confidence distribution of the sliding window state fusion
本文将整个系统的评估结果分为3个不同的等级,可靠、一般和不可靠,每个时刻三者置信度之和为1。由图2和图3可以看出,系统被评估为可靠的置信度在逐渐减小,被评估为一般的置信度基本保持不变,而被评估为不可靠的置信度在不断增加,说明系统整体的可靠性程度是逐渐下降的。
为了更好地验证所提方法的有效性,将上述结果使用效用的概念转化为数值输出的形式。设定系统评价为可靠性等级的效用为μ(F1)=1,评价为一般性等级的效用为μ(F2)=0.5,评价为不可靠等级的效用为μ(F3)=0。综合考虑三者,按照期望效用的格式输出,结果如图4所示。需要说明的是,图中振动信号是根据专家经验以及轴承退化的水平方向和竖直方向的振动信号综合作用得到的轴承退化趋势。可以看出,本文方法与振动信号呈现整体相同的退化趋势,可以较明确地反映轴承退化情况。

图4 本文方法的评估曲线Fig.4 The evaluation curve of the method in this document
本文方法评估结果与提取振动信号有效值A[27]的对比如图5所示。可以看出:初始时刻轴承处在一个运行状况良好的阶段,因此初始一段时间可靠度较高,振动信号有效值也很小;但是,随着使用可靠度开始逐渐降低,振动信号有效值也开始升高,在同一时刻二者的变化趋势是相对应的;之后,振动信号有效值开始出现减小的趋势,此时可靠度也有明显增加的趋势;随着进一步的退化,振动信号有效值开始增大得更加明显,而可靠度曲线也开始进一步下降。通过二者的对比可以很好地验证本文方法评估轴承可靠度的有效性。提取振动信号有效值方法虽然简单易行且相对直观,但是不能反映轴承早期微弱故障阶段的特征,如图5所示的初始一段时间内,振动信号有效值的变化趋势基本不明显,而本文方法可以直接反映轴承的退化趋势。提取振动信号有效值方法提取了振动信号水平方向和竖直方向的有效值,二者得到的结果存在一定的区别,无法获取综合的结果,而本文方法得到的是综合值。因此,本文方法相较于提取振动信号有效值方法更有效。

图5 本文方法评估结果与提取振动信号有效值对比 Fig.5 The results of this article are compared with the results of extracting valid values
根据最优窗口确定的规则,对指标融合后得到的安全性状态的置信分布进行转化,得到数值输出结果。经过不同窗口大小的滑动平均,最终得到的结果如图6所示。
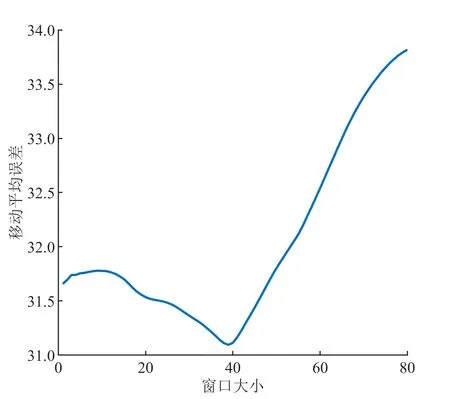
图6 最优窗口大小的确定Fig.6 Determination of the optimal window size
与文献[17]所提的三状态重要性一致的方法进行对比,结果如图7所示。可以看出:在初始一段时间内,轴承的性能还没有发生退化时,两种方法得到的可靠度都是接近1;随着轴承使用,不可避免地发生退化,二者得到的趋势与振动信号反映的退化趋势一致。但是,本文方法得到的可靠度曲线更加平滑,而文献[17]方法得到的可靠度曲线振荡比较明显。根据实际情况可知,轴承的退化程度不可能在下降和上升之间持续振荡。而且,在最终时刻,文献[17]方法显示轴承的可靠度急剧下降,但是本文方法所得结果与实际振动信号反映的退化趋势一致,基本稳定在0.4附近。文献[17]方法所得可靠度均方误差为0.028 1,而本文方法的为0.016 7,更符合实际情况。这是因为文献[17]在对历史、当前和未来时刻安全性状态的重要性分析时,假设三者重要性一致。然而,本文根据Kriging的思想,考虑越靠近当前时刻权重越大,这样得到的结果更加符合实际。

图7 轴承可靠性评估结果Fig.7 Reliability assessment of bearings
5 结 论
本文在现有的大型复杂系统在线可靠性评估方法的基础上,针对未来时刻所包含的不确定性信息和假设历史、当前和未来时刻安全性状态的重要性一致会造成历史和未来时刻安全性状态权重过大的问题,提出一种采用滑动窗口与克里金插值算法的复杂系统可靠性评估方法。本文首先介绍了所研究问题的基本模型及需要解决的问题,接着对证据推理算法进行了简单的介绍,然后介绍了滑动窗口模型,采用任何给定的窗口大小的移动平均误差都会随着接近时间序列的实际窗口大小而减小的思想,得到最优的窗口大小,以便对历史数据进行选择并动态更新数据,使用Kriging的思想对权重进行自适应调整,最后使用基于权重自适应调整策略的可靠性评估准则对整体的可靠性进行评估。以西安交通大学的轴承退化数据对本文方法进行验证,并与文献[17]方法在两种工况下进行了对比,实验结果充分验证了本文方法的有效性。本文方法是基于数据的,因此针对退化数据充足的系统一般都适用。
