沿流向放样的轴流压气机叶道设计方法
2023-05-05赵奕博李浩琚亚平张楚华
赵奕博,李浩,琚亚平,张楚华,3
(1. 西安交通大学能源与动力工程学院,710049,西安; 2. 上海交通大学机械与动力工程学院,200240,上海; 3. 西安交通大学机械结构强度与振动国家重点实验室,710049,西安)
轴流压气机作为航空发动机、燃气轮机和工业压缩系统的核心部件之一,其内部流动具有三维、非定常、黏性、可压缩性等特点[1]。经历过去几十年研究后,轴流压气机整体气动性能有显著提升,但仍面临端区流动损失较大且难以调控的难题。如何实现端区流动的精细化组织和控制是突破压气机性能极限的关键所在。从流动控制角度而言,压气机端区流动控制方法可分为被动控制和主动控制两类。其中,前者包含非对称端壁[2]、前缘边条[3]、叶身融合等方法,相比于后者具有无需添加附加装置、结构简单等优点,旨在通过重新设计叶片角区和端壁结构,改善近壁区流场分布,抑制或消除端区流动分离、减弱二次流及其影响,在高负荷轴流压气机中具有较好的应用前景[4]。
在轴流压气机非对称端壁研究方面,Atkins[5]、Rose等[6]先后采用实验和数值模拟方法开展研究,发现非对称端壁能够改善叶片尾缘后静压分布特性。Brennan等[7]通过数值研究发现,非对称端壁可以提高压气机效率、减小出口旋转角变化,但压力损失增大。李国君等[8-9]将数值模拟和实验相结合,发现非轴对称端壁减小了端部压力面与吸力面之间的压差,减弱了通道涡强度,达到了降低二次流损失的目的。Hergt等[10-11]将数值模拟和实验相结合,发现加入非对称端壁后近壁面流体被偏转移向下游,减弱同吸力面侧边界层的交互作用。Chu等[12]构建了非对称端壁理论模型,并将其应用于高负荷压气机中,结果显示二次流和流动损失得到有效改善。
在轴流压气机前缘边条和叶身融合研究方面,Debruge等[13]通过实验研究发现,前缘边条可以提高叶片气动性能。Goodhand等[14-15]通过数值研究发现,边条对压气机性能影响较大,去除边条后流动损失增加18%,有边界层分离现象时边条作用更加显著。季路成等[16-18]提出叶身融合技术,对局部角区结构进行几何参数化和设计优化,研究发现叶身融合结构可以有效消除角区分离和减轻前缘马蹄涡,并大幅提升压气机负载能力。
从上述研究可以看出,非对称端壁、前缘边条和叶身融合方法为改善端区附近流场分布、提升压气机气动性能提供了有效途径,但这些研究均是基于基元叶型+径向积叠的常规设计体系[19],该体系中端区控制和叶型控制线关联性弱,本质上难以将压气机叶片、角区和端壁结构进行协同考虑,更难以实现叶片到端壁的高阶光滑过渡,限制了端区流动的改善及压气机性能的提升空间。为此,本文打破惯有思维,创新性地提出了一种轴流压气机叶道设计新方法,通过将若干横截面沿流向进行放样生成压气机叶道,实现叶片、角区和端壁几何的联合调控和高阶光滑融合,以解决前述难题,并以NASA Rotor37为例,验证所提出方法的有效性。研究成果有望为发展轴流压气机先进设计方法提供新的思路。
1 沿流向放样压气机叶道设计方法
1.1 叶道流向放样几何定义
如图1所示,与常规压气机的基元叶型+径向积叠的定义方法不同,本文所提出的沿流向放样的轴流压气机叶道几何包含5个元素:前缘面周线A1B1C1D1、尾缘面周线A3B3C3D3、中间截面周线如A2B2C2D2及叶顶线A1A2A3、B1B2B3和叶根线C1C2C3、D1D2D3。其中,前缘面周线A1B1C1D1由前缘线A1D1(B1C1)、前缘轮毂线C1D1和前缘机匣线A1B1构成,尾缘面周线A3B3C3D3由尾缘线A3D3(B3C3)、尾缘轮毂线C3D3和尾缘机匣线A3B3构成,中间截面周线A2B2C2D2由叶片交线A2D2(B2C2)、中间轮毂线C2D2和中间机匣线A2B2构成。根据该定义,压气机叶道经前缘面周线A1B1C1D1、若干中间截面周线如A2B2C2D2与尾缘面周线A3B3C3D3放样生成,叶顶线A1A2A3、B1B2B3和叶根线C1C2C3、D1D2D3是放样过程的引导线。显然,在该定义方法中,各截面周线的空间位置能直观反映压气机叶片的弯扭掠特征,通过控制各截面周线几何坐标,可容易实现压气机叶片、角区和端壁结构的协同设计及叶片到端壁的高阶光滑过渡。

图1 叶道定义方法Fig.1 Geometric definition of blade passage in compressor
压气机前/尾缘面周线与叶顶/叶根线由原始叶片的几何数据得到,中间若干截面周线计算思路如下。
对子午面内轮盖和轮毂的曲线数据进行平均,得到子午面几何中心线

(1)
式中r和z分别表示径向坐标和轴向坐标。在流向不同位置处(如图1中的E处)做子午面内几何中心线的垂线(如图1中的FG),该垂线是子午面内直线,将其绕旋转轴旋转,获得旋转面,该旋转面与叶片曲面的交线(如图1中的A2B2C2D2)即为叶道中间截面周线。在流向不同位置处作垂线并旋转,即可得到不同位置处的中间截面周线。
1.2 叶道几何参数化建模
根据上述叶道几何定义方式,分别对叶道前/尾缘面周线、中间截面周线、叶顶/叶根线进行几何参数化建模(如图2所示),建模方法如下。
(1)前/尾缘面周线。如图2(a)所示,采用4阶Bezier曲线[20-21]描述叶片前/尾缘线。其中:前缘线控制点V3~V5沿±z和±θ两个方向变动,尾缘线控制点V8~V10沿±θ方向变动;采用2阶Bezier曲线描述叶片前/尾缘与轮毂之间的过渡线,即前/尾缘边条,边条控制点V1和V11沿±z方向变动以控制边条轴向延展区域,控制点V2和V12须分别沿前尾缘线变化以控制边条径向延展区域并确保高阶连续;待控制点V1与V11位置确定后,采用3阶Bezier曲线描述前/尾缘截面轮毂曲线,控制点V6、V7及V13、V14均沿±r方向变化以实现非对称端壁几何的灵活控制。综上可知,共需17个设计变量控制前/尾缘面周线几何,其中前缘面10个、尾缘面7个。
(2)中间截面周线。如图2(b)所示,采用3条3阶Bezier曲线分别描述叶片交线与中间轮毂线,控制点V15、V16、V19、V20沿±θ方向变动以控制叶道两侧形状。考虑到叶片强度,控制点V15、V16、V19、V20改变后需校核叶片重心分布,保证叶片重心在一条直线上。控制点V23、V24沿±r方向变化以实现非对称端壁几何的灵活控制;采用两条2阶Bezier曲线生成叶片与轮毂的过渡线以实现叶身融合,控制点V17和V21沿叶片交线变化以控制叶身融合径向位置,V18和V22沿中间截面轮毂线变化以控制叶身融合周向位置。综上可知,共需10个设计变量控制1个中间截面周线,本文采用3个中间截面,故共有30个设计变量。
(3)叶顶/叶根线。如图2(c)所示,为保证叶顶线和叶根线在前/尾缘处光滑过渡,采用3段Bezier曲线分别描述其首尾与中间部分。具体地,叶顶/叶根中间部分曲线由5阶Bezier曲线生成,叶顶/叶根首尾部分曲线由3阶Bezier曲线生成。已知机壳型线,待叶顶线确定之后,方可获得叶顶间隙叶道几何。本文中,叶顶线和叶根线固定不变。
综上可知,采用所提出的沿流向放样的压气机叶道设计方法对单排叶道进行参数化造型,共需47个几何设计变量,其中叶片区域设计参数为33个。若考虑设计成本,针对具体研究对象可适当调整参数化曲线阶次与中间截面数以降低设计变量数目。需要指出的是,上述方法不仅适用于对轴流压气机动叶通道进行参数化表征,对静叶通道及进/出口管道的参数化表征也同样适用。
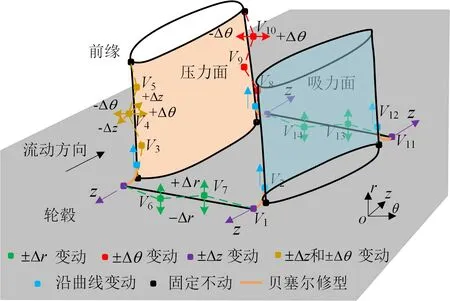
(a)前/尾缘面周线
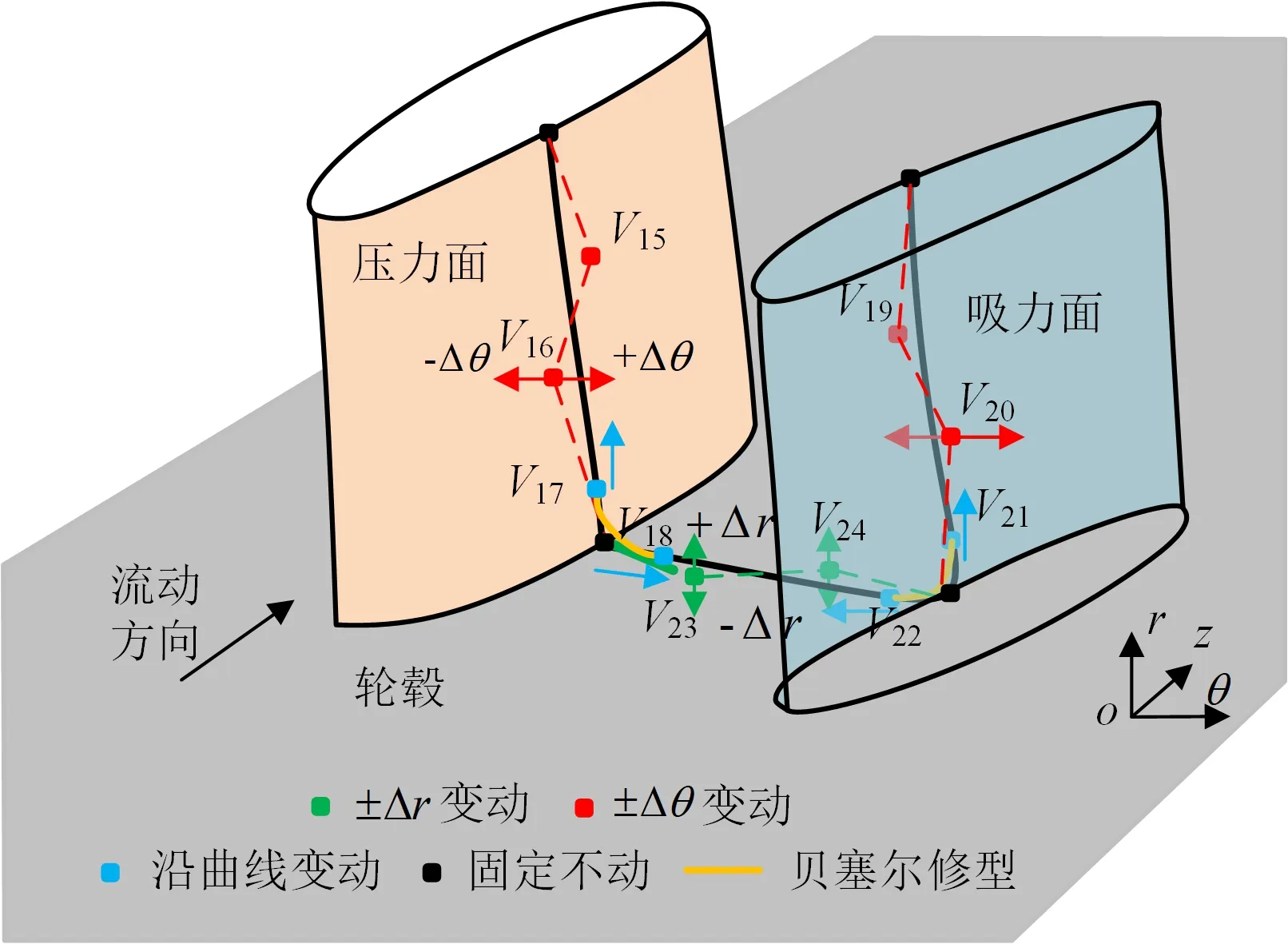
(b)中间截面周线

(c)叶顶/叶根线
2 数值计算方法
2.1 研究对象
压气机转子NASA Rotor37原始模型的运行参数如表1所示[22]。采用上述叶道定义新方法和参数化造型方法分别对其进行重构和参数化造型,并通过改变叶根和端壁处结构参数进行改型设计,下文分别针对原始模型、重构模型、参数化模型和改进模型的气动性能和内部流场进行对比分析。

表1 NASA Rotor37设计及运行参数
2.2 数值方法
采用NUMECA FINE/Turbo软件求解三维定常雷诺平均Navier-Stokes(N-S)方程,求解压气机气动性能及内部流场,补充Spalart-Allmaras湍流模型保证方程组封闭,方程对流项采用二阶中心差分格式并添加人工黏性进行离散,时间推进项采用4阶显式Runge-Kutta法,采用多重网格、隐式残差及当地时间步等技术加速收敛过程。采用单通道计算模型,计算区域进口给定总温(288.15 K)、总压(101 325 Pa)并设置轴向进气,出口给定静压分布,由径向平衡方程获得[22],叶片表面及端壁均设置为无滑移绝热条件,周期性边界设置周期性边界条件。基于Numeca Autogrid5在计算区域内生成结构化计算网格,如图3(a)所示。叶片表面采用HOH拓扑结构,叶顶、叶根间隙采用O4H拓扑结构,对于改进模型,叶根处采用蝶形网格。此外,通过对近壁面处网格进行局部加密,确保y+≤10。
图3(b)展示了不同网格数下计算出的原始模型的气动性能对比。可以看出,当网格数从40万增加到80万时,压气机的性能曲线基本不变,表明当计算网格数为40万时,已达到网格无关性。在下文计算中,原始模型、重构模型和参数化后模型的网格数均在40万左右,而改进模型由于在前尾缘边条及叶身融合等部位进行网格加密处理以辨识细微几何,计算网格数约为70万。

(a)网格划分结果

(b)性能曲线对比
图4和图5展示了原始模型、重构模型与参数化后模型的气动性能曲线和流场分布与实验数据对比情况。可以看出:原始模型的等熵效率与实验数据最大绝对误差小于2个百分点,总压比计算结果与实验数据最大相对误差小于3.7%,说明数值计算模型具有较高的精度;重构模型与原始模型相比等熵效率最大绝对误差小于0.8个百分点,总压比最大相对误差为2.1%;参数化模型与原始模型相比,等熵效率最大绝对误差小于0.44个百分点,总压比最大相对误差为1.44%,原始模型预测的气动性能与流场分布与实验数据基本一致。显然,原始模型、重构模型与参数化模型的整体气动性能吻合良好,说明所提出的叶道沿流向放样定义方法和参数化建模方法的可行性。

图4 性能曲线对比Fig.4 Comparison of aerodynamic performance
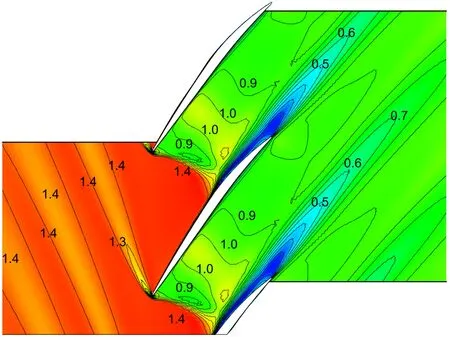
(a)预测结果

(b)实验数据[23]
3 轴流压气机叶道改型设计
3.1 压气机叶道改型
为验证所提出的沿流向放样叶道设计方法的先进性,本小节采用均匀设计实验设计方法生成不同叶道几何,通过优选实现原始叶道的改型设计,并分析改型前后气动性能和流场的变化。考虑到吸力面角区和前缘边条结构对压气机气动性能影响较大,选取吸力面侧角区控制变量和前缘边条控制变量(即图2中的V21、V22与V1、V2)为设计变量,其具体变化范围如表2所示。值得注意的是,在改型过程中,须调整轮毂参数以维持通流面积不变[24]。
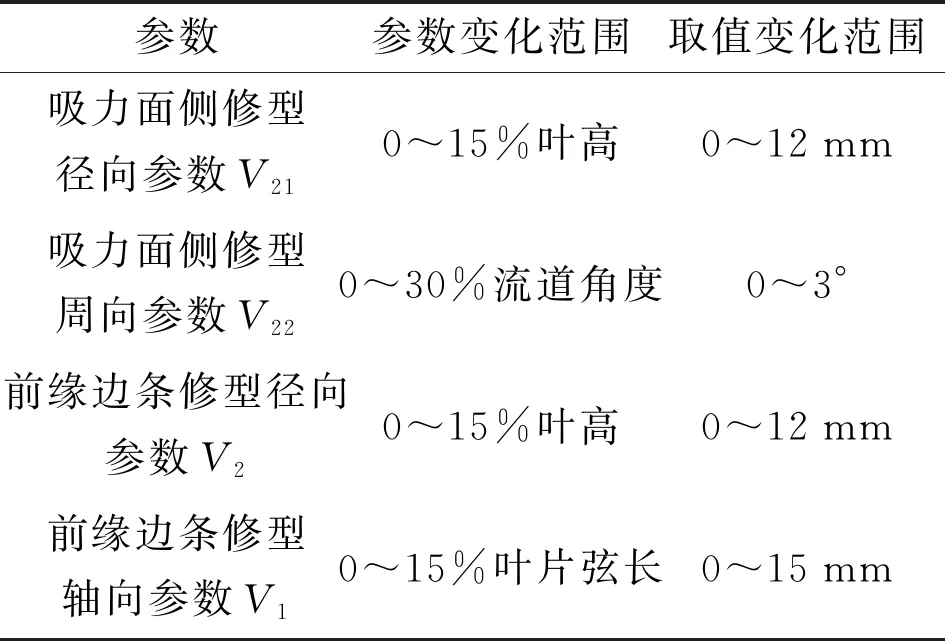
表2 改型参数变化范围
运用均匀实验设计表U9(96)生成9个样本,并基于前述数值模拟方法对每个样本的气动性能进行计算分析[25]。图6对比了气动性能最优的改型叶道与原始模型叶道几何。相比于原始模型叶道,改型叶道具有明显的前缘边条和叶身融合特征,且端壁有所下凹,吸力面角区径向参数V21的r坐标增加5 mm,周向参数V22的θ坐标减小1.8°,前缘边条轴向参数V1的z坐标减小5.75 mm,径向参数V2的r坐标增加3.25 mm,端壁控制点V23、V24的z坐标减小0.718 0 mm,生成的压气机流道端壁最大下凹0.65 mm。

(a)原始模型
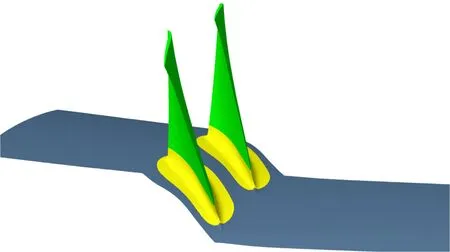
(b)改进模型
原始模型与改进模型的气动性能对比如图7所示。可以看出,改型前、后通流能力不变,最高效率点均为20.77 kg·s-1,可见下凹的非对称端壁结构可以弥补叶身融合对通流面积和通流能力的影响。相比于原始模型,改进模型最高等熵效率提升0.3个百分点,总压比提升2.43%,且喘振裕度显著提升。喘振裕度定义为稳定边界线和共同工作线上的压比之差除以共同工作线上的压比,按等转速换算且考虑换算流量变化影响的定义式为

(2)
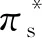
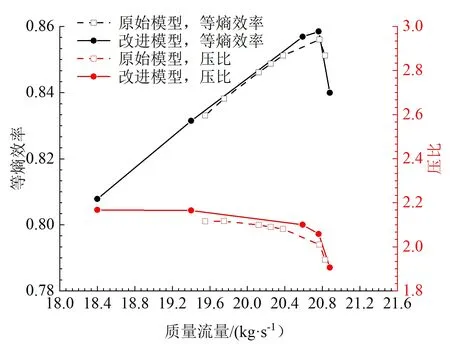
图7 改型前后压气机的气动性能对比Fig.7 Comparison of aerodynamic performance of the rotor before and after design modification
3.2 流场分析
为深入探究改型后整体效率提高、喘振裕度拓宽的原因,首先得出改型前后设计工况(20.77 kg·s-1)和近失速工况(19.54 kg·s-1)下的出口总温、总压和等熵效率分布图,如图8和图9所示。

图8 改型前后设计工况下出口总压、总温、等熵效率沿叶高的分布Fig.8 Comparison of spanwise distributions of total temperature, total pressure and isentropic efficiency before and after design modification at design point
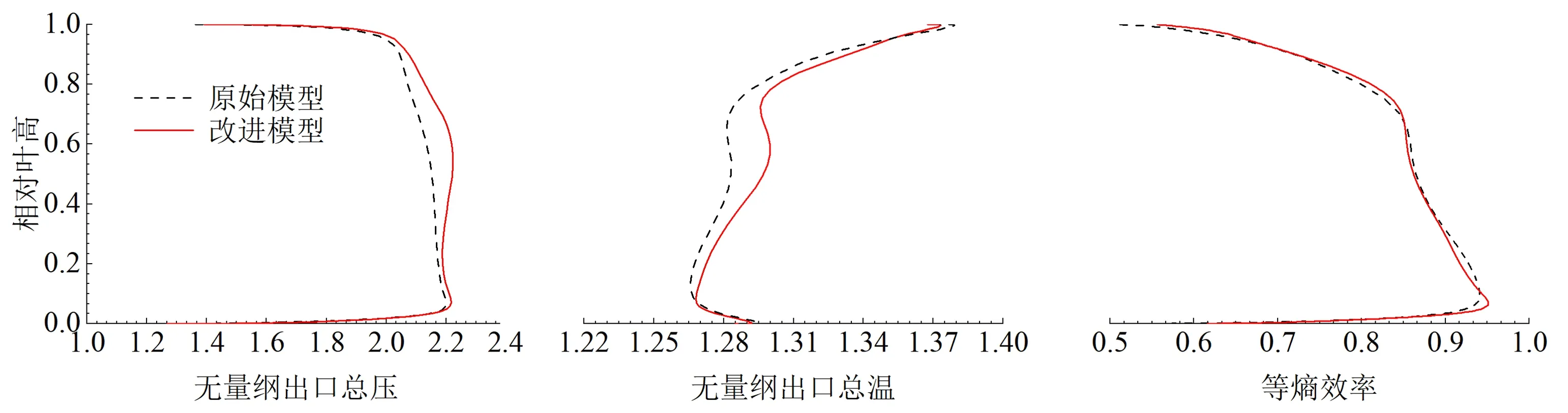
图9 改型前后近失速工况下出口总压、总温、等熵效率沿叶高的分布Fig.9 Comparison of spanwise distributions of total temperature, total pressure and isentropic efficiency before and after design modification at near stall point
可以看出,改型后叶中区域总压、总温改变明显,压气机8%叶高以下及约50%叶高以上的等熵效率均有提高,而在中间叶高处等熵效率略有下降。相比设计工况,近失速工况下靠近叶根处流动效率提升更加显著,表明叶身融合结构可以减少叶根处流动损失,且近失速工况下作用更加显著,下文将针对流场继续进行分析。
图10和图11分别对比了设计工况和近失速工况下改型前后叶根、叶中、叶顶截面相对马赫数云图分布。可以看出:设计工况下,由于改型叶道主要改变了角区结构,叶根处叶背激波强度减弱,叶中和叶顶处马赫数分布变化不显著;近失速工况下,改进模型流动状况明显改善,各叶高处叶背激波强度和尾迹区均有所减小,流动分离减少,稳定性增强。

(b)改进模型
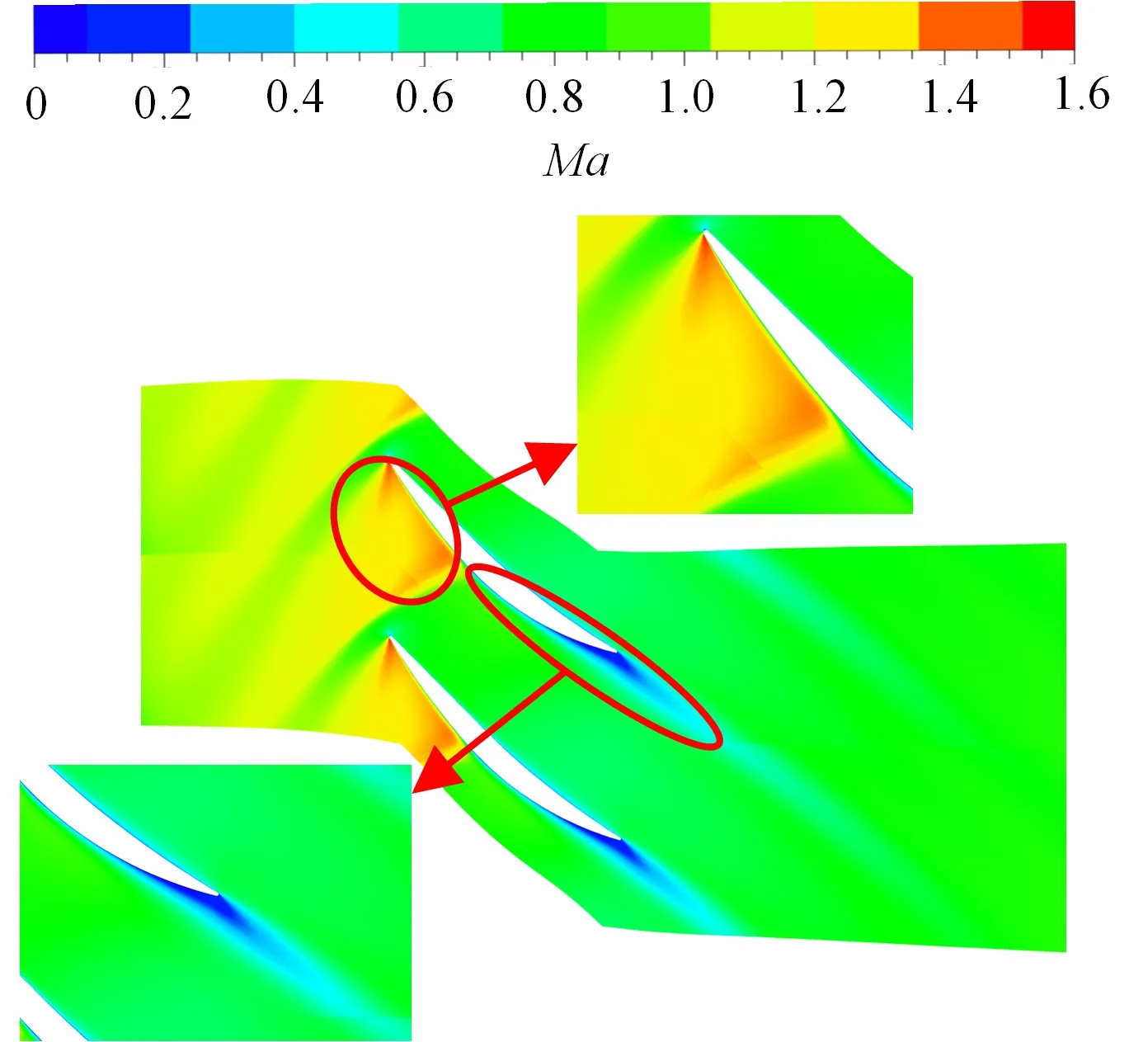
(a)原始模型5%叶高

(b)改进模型5%叶高

(c)原始模型50%叶高

(d)改进模型50%叶高

(e)原始模型95%叶高
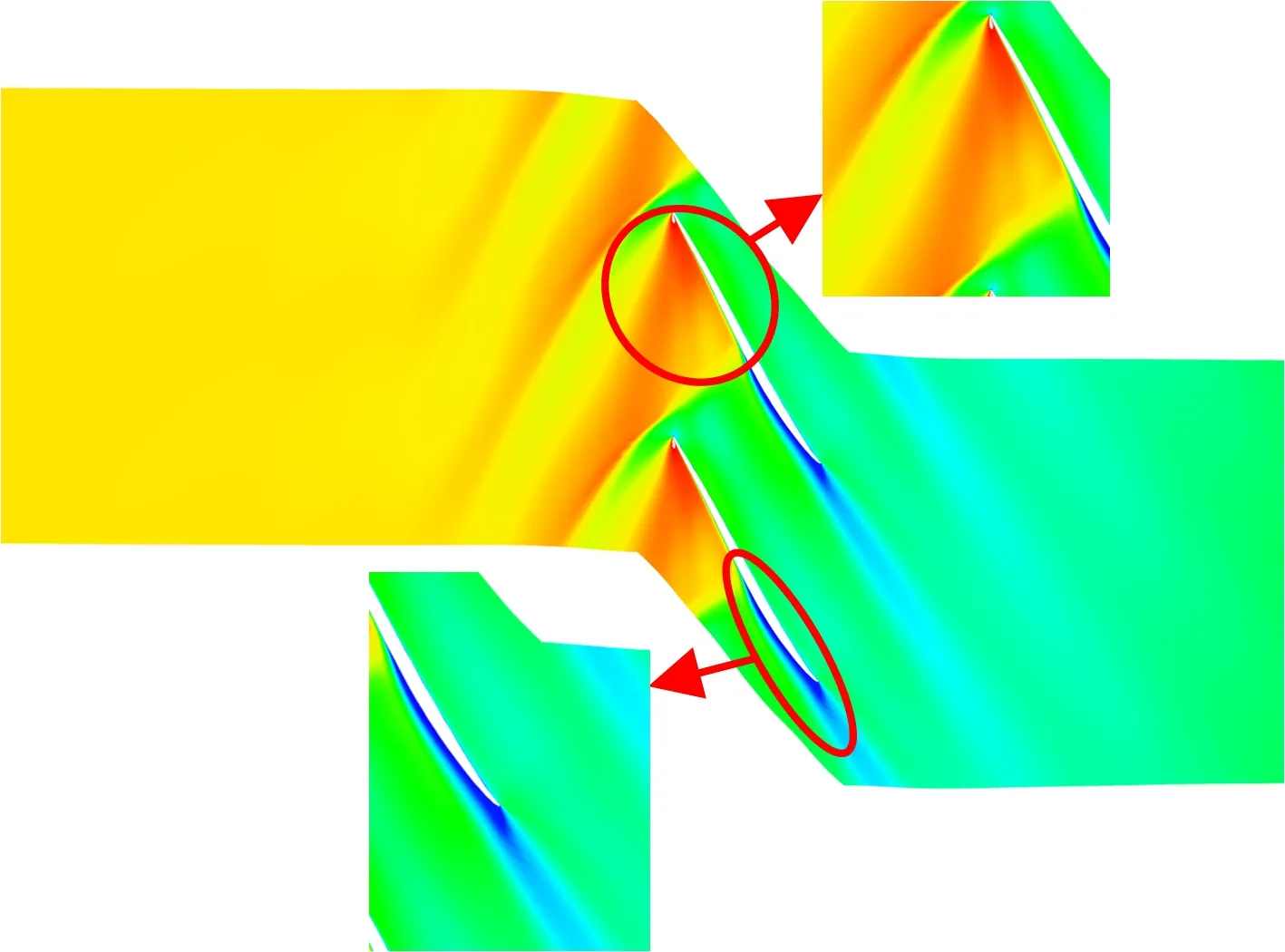
(f)改进模型95%叶高
图12和图13分别给出了设计工况和近失速工况下叶片静压系数和近壁面流线分布。叶片表面静压系数Cp[26]能够展示叶片负载分布情况,定义为
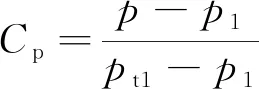
(3)
式中pt1、p和p1分别表示压气机进口平均总压、当地静压和进口静压。从图中可以看出,叶身融合结构实现了叶片与端壁的高阶光滑过度,提高了叶片叶根处静压系数,从而增大了从叶根到主流区的压力梯度,诱导叶根处低能流体向主流区迁移。同时,前缘边条结构向前探伸的细长边条同样能够诱导前缘叶根附近低能流体流向主流区。低能流体的径向迁移一方面能够避免其在叶根处聚集,减少角区附近流动损失。另一方面,通过加强与主流区流体的动量交换,使得角区分离现象得到缓解,在近失速工况下尤为明显(如图13所示),喘振裕度因而拓宽。此外,叶根处低能流体的径向迁移又会使得主流区损失轻微增大(如图8(c)所示)。总之,叶身融合结构和前缘边条结构通过诱导叶根附近低能流体径向迁移,使得压气机整体效率有所提升,喘振裕度得到拓宽。
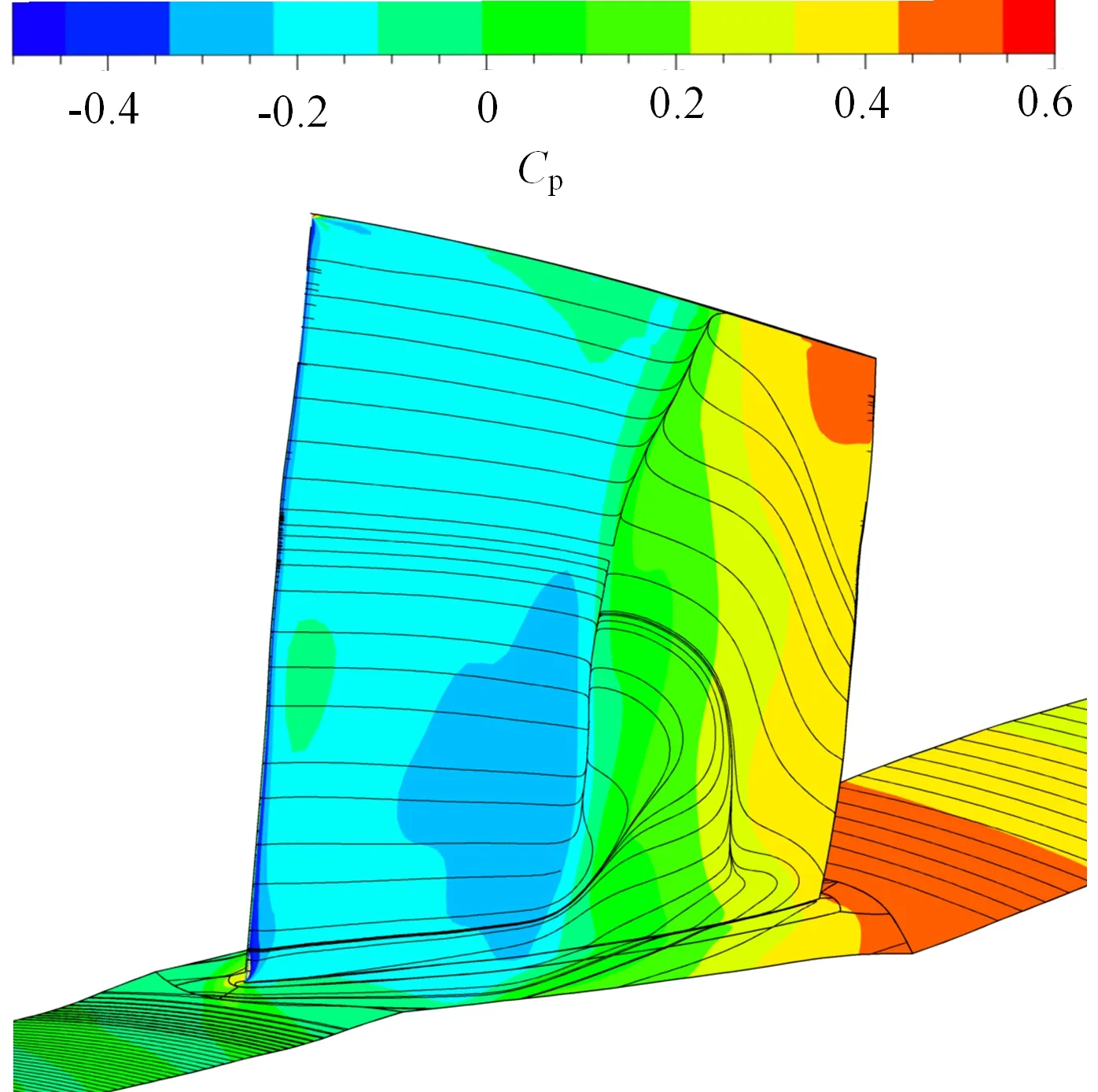
(a)原始模型
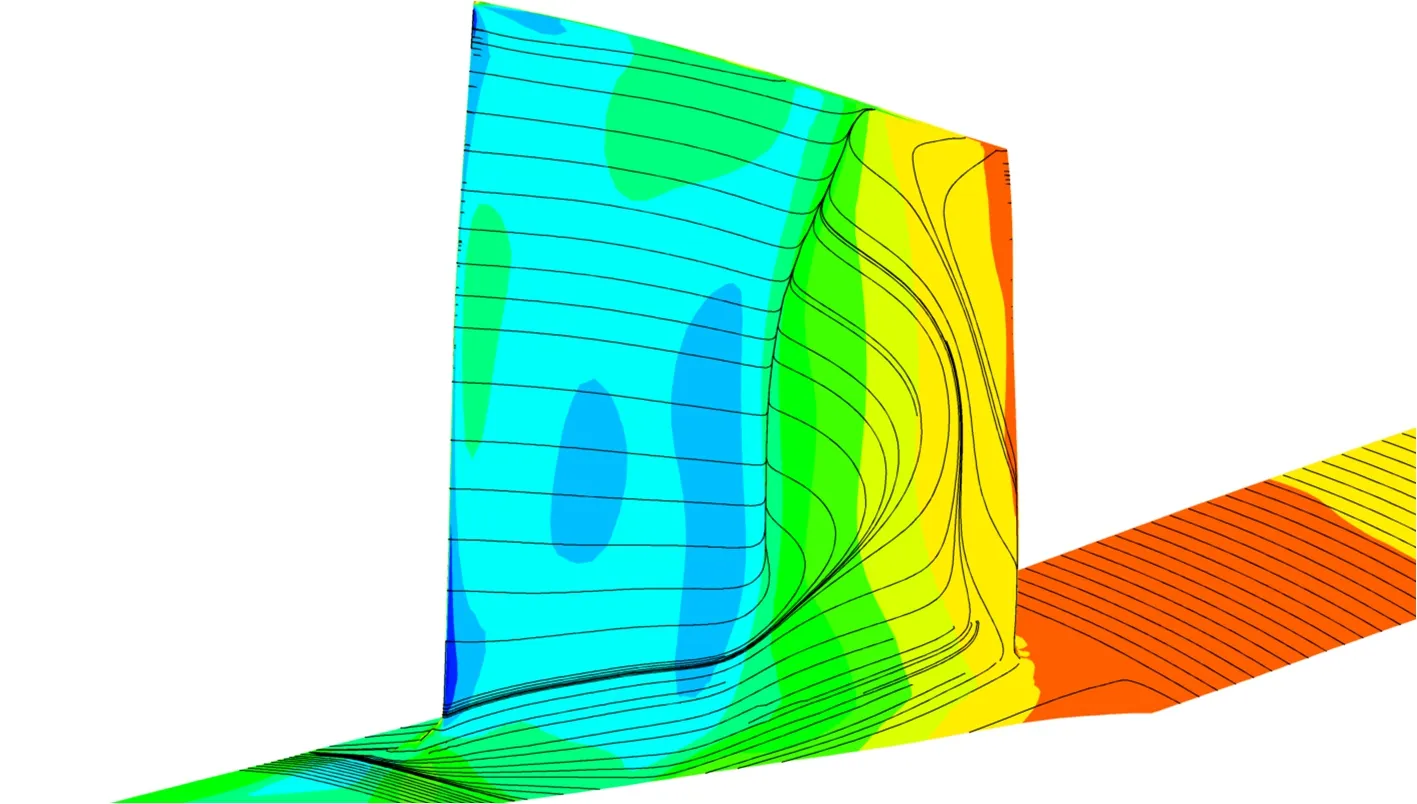
(b)改进模型

(a)原始模型

(b)改进模型
4 结 论
本文提出了一种轴流压气机的叶道定义与参数化建模新方法,叶道经前缘面周线、若干中间截面周线与尾缘面周线放样生成,叶道参数化后包含47个控制参数,应用于NASA Rotor37完成了叶道重构与角区改型,得到以下结论。
(1)采用沿流向方向放样的轴流压气机叶道设计方法,实现了压气机叶片、角区和端壁结构的协同设计及叶片到端壁的高阶光滑过渡。针对 NASA Rotor37完成了叶道改型,改型后的压气机动叶设计工况等熵效率提高了0.3个百分点,总压比提高了2.43%,喘振裕度由11.85%增加至18.8%。
(2)叶身融合和前缘边条结构通过诱导叶根附近低能流体的径向迁移,减少角区处流动损失,延缓流动分离现象。非对称端壁能够弥补叶身融合结构造成的通流能力下降,下凹端壁可以帮助稳定压气机通流能力。叶片、叶身融合、前缘边条、非对称端壁结构的合理配置是充分发挥叶道设计方案优势的重要前提,后续将继续基于本文提出的轴流压气机叶道设计方法开展压气机整机设计优化。
