低温可视化力学装置传热分析与计算研究

吴姗姗,王珏,张恒成,刘辉明,黄传军,黄荣进,李来风,周远

(1. 中国科学院理化技术研究所航天低温推进剂技术国家重点实验室,100190,北京;2. 中国科学院大学,100049,北京; 3. 航天科工空间工程发展有限公司,100854,北京)

材料的低温力学性能与实际工程应用息息相关,ITER计划通过全超导Tokamak产生的强磁场来实现大规模的核聚变反应[1-2]。然而,超导线缆产生强磁场时在电磁力的作用下容易发生变形甚至破坏,从而影响超导磁体正常运行[3-4]。超导磁体在极端温度(4.2 K)下运行,此过程中材料的力学性能发生改变[5]。因此,超导磁体材料以及线圈外部的保护夹套在工作环境下的力学性能是保证超导磁体安全运行的重要因素[6]。此外,材料的低温性能在航空航天液体燃料储存系统、材料改性等应用中也引起了众多学者的关注。材料的力学性能与材料的成分、组织结构、结构缺陷以及材料所处的环境温度有关,特别是在低温下应用时,其力学性能与室温下截然不同[11-13]。以金属材料为例,面心立方的金属在低温下仍具有较好的韧性与强度,体心立方的金属在低温下易发生低温脆性,而316LN不锈钢材料在低温环境中则会发生应力诱导马氏体相变,因此需要了解材料随温度变化的综合力学行为[14-15]。

在材料的变形测试中,位移和应变是保证测量精度的重要数据,而机械引伸计测量和光学测量是应变测量中常用的方法。其中机械引伸计受测量环境(温度、震动)的影响大,且测量范围有限,无法测量位移场及应变场,在使用时受到诸多限制[16]。数字图像相关(DIC)光学测量方式是通过对比试样变形前后的数字图像来获取力学性能的测试方法,可以对试样表面进行高精度全场动态测量[17-22],本文中的低温力学性能测试装置采用后者对试样进行测量。

为了将3D-DIC技术应用到材料的低温变形测试中,需要为试样提供便于采集数字图像的低温环境。目前,常用的低温冷却方式包括低温液体冷却和制冷机冷却两种方法。低温液体冷却包括液氦(4.2 K)、液氢(20.3 K)、液氮(77.4 K)和液化天然气(111 K)等,这种冷却方式是通过低温液体的汽化潜热和气体显热将物体进行冷却[23-26]。然而,低温液体会使采集到的数字图像出现扭曲与变形,低温氦气的热对流也会引起折射率的变化,从而使相机拍到的数字图像模糊,影响DIC方法测量的准确性。制冷机冷却方式通过有效的传热方式将物体温度在一定温度范围内连续、可调、可控地降低,且无需采用其他低温工质[27-29],本文采用制冷机冷却的方式来提供连续可调可控的低温环境。由于低温装置需要配置光学窗口,其发射率较大,无疑增加了被测样品与外界的辐射换热量,且制冷机在低温下提供的冷量有限,为了在更低温度下测得材料的力学性能,需可靠估计低温装置内的漏热量,选取直观的传热分析方法尤为重要。

本文首先介绍了4.2～300 K温区内材料力学性能测试的可视化低温装置的几何结构,并对装置进行了传热过程分析;其次,对此研究对象中各部件之间的传热关系进行了介绍,并分别采用了COMSOL、Sage软件对试样进行传热计算;最后,分析对比了两种计算方法的温度分布,并基于Sage研究了试样尺寸、试样发射率、窗口尺寸、窗口表面发射率对试样温度分布的影响,为低温装置中传热分析与计算提供理论参考。

1 研究对象及传热过程分析

本文中低温DIC力学性能测试系统的结构具有不同的换热方式,需要对其进行理论传热分析。

1.1 研究对象

本装置中使用的3D-DIC光学成像系统主要由两台高速摄像机和普通白光组成,其中DIC测量系统主要包括光学成像系统、光电转换传感器和数字图像处理系统,光学成像系统将试样表面的散斑图像通过摄像机读取至图像卡中,通过计算机中的数字图像处理系统将图像进行相关计算转换。低温-DIC力学性能测试装置结构及其传热关系示意图如图1所示,整个装置为偏置式,真空罩和辐射屏上分别开设了两个窗口,一个为50 mm×230 mm的矩形石英玻璃窗口,另一个为Ф50 mm的圆形石英玻璃窗口。真空罩内真空度可达1.3×10-5Pa。试样测试前需均匀喷涂一层哑光漆便于图像识别,两台相机在竖直方向上通过两层矩形窗口呈15°～45°对试样表面进行图像采集,白光光源通过两层圆形窗口在试样表面形成均匀光场。 低温力学测试装置内主要部件如图1(b)所示,真空罩、支撑管与夹具均为不锈钢材质,拉伸杆为钛合金材质,辐射屏、热桥以及制冷机冷头为铜质,矩形窗口和圆形窗口均为石英玻璃,热桥与连接端面均匀涂覆Apiezon N脂并压接。真空罩内部在实验过程中始终保持真空,两台住友RDK-415D制冷机作为冷源安装在真空罩法兰上,辐射屏通过制冷机一级冷头连接并冷却,制冷机二级冷头通过铜质柔性热桥连接至力学拉伸部件使其冷却。力学拉伸组件主要由拉伸杆、支撑管、拉伸夹具组成,拉伸杆直接连接真空罩法兰(室温端,300 K)和低温夹具(低温端,4.2 K),支撑管分别连接真空罩法兰、辐射屏以及低温夹具,夹具通过热桥与冷头相连,且直接与试样接触。

(a)低温-DIC装置外部示意图

(b)装置内部几何结构及传热关系示意图

1.2 传热过程分析

热量通过拉伸杆和支撑管从高温端向低温端传导,材料的导热换热量为

(1)

式中:A为横截面积;L为导热长度;ks为热导率,是固体材料温度依赖的特性;Qcond为净热流。

除热传导外,部件间的辐射传热亦不可忽略。装置内存在温差的部件间皆存在辐射换热,如真空罩与辐射屏间的辐射换热Qrad1、辐射屏窗口与试样间的辐射换热Qrad2-1、辐射屏窗口与拉伸组件表面的辐射换热Qrad2-2、辐射屏对制冷机组件的辐射换热Qrad3、辐射屏与拉伸组件表面的辐射换热Qrad4以及辐射屏与试样间的辐射换热Qrad5等。

两表面间的辐射换热量为

Qrad=A1X1,2J1-A2X2,1J2

(2)

(3)

式中:Qrad为两表面间的辐射换热量;A1、A2分别为两辐射表面的辐射面积;X1,2、X2,1分别为从表面1到表面2的角系数和从表面2到表面1的角系数;Ji为i表面的有效辐射力;εi为i表面的表面发射率;C0为黑体辐射系数,其值为5.67 W/(m2·K4);Ti为i表面的温度。

在实验过程中,真空罩内恒为高真空(10-4Pa)环境,因此忽略对流换热。若Th、Tl、Ts在此装置内分别表示室温、低温以及辐射屏温度,根据以上装置结构和传热分析结果,与试样有关的导热和辐射换热关系可表示为热阻关系图,如图2所示。热阻R可表示为

(4)

式中:ΔT为物体两端的温差;Q为辐射换热量或导热换热量。

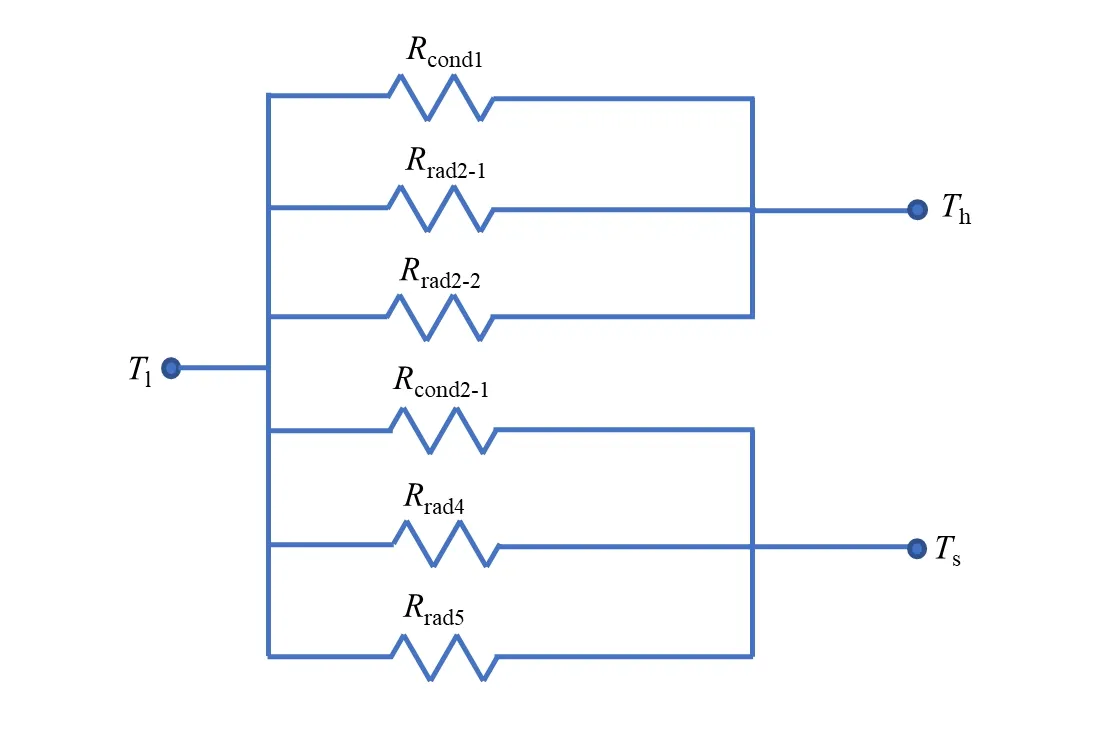
(a)低温端Tl向室温Th及辐射屏Ts间的传热

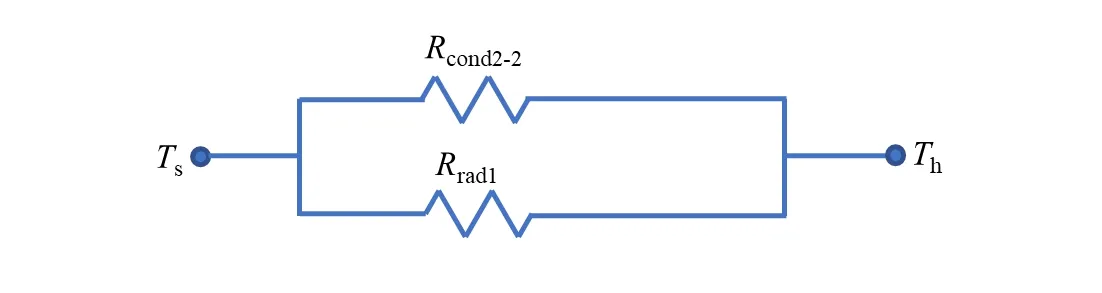
(b)辐射屏Ts向室温Th的传热

2 模型简化及计算方法

为了探索更准确简洁的传热计算方法,针对上节中的几何模型和传热关系,首先使用COMSOL三维求解方法计算了各个传热结构的传热量,然而此方法所需的计算模型复杂,且计算时间较长。因此,使用Sage一维求解方法分别开发出导热模型和辐射模型,此方法的计算成本显著降低。

2.1 COMSOL三维求解

COMSOL Multiphysics可将单一类型物理场扩展到耦合的物理场模型,且可以同时进行计算。对整个低温力学拉伸装置建立涵盖两台制冷机、真空罩、辐射屏、石英窗口、被测试样、拉伸夹具、拉伸杆、支撑管、热桥等结构的三维辐射场与导热场的耦合求解域物理模型。根据以上结构分析与传热分析结果,在COMSOL软件仿真中做出如下假设:①除与热桥接触的界面外,其余所有界面间为理想接触;②所有参与导热的结构温度呈线性分布;③玻璃窗口与真空罩、辐射屏的温度始终保持一致。

首先建立几何模型,为节约软件计算成本,三维耦合求解时只关注辐射屏以内的传热情况。用于COMSOL软件的三维简化几何模型如图3所示,辐射屏内部为制冷机、热桥、夹具、试样、拉伸杆、支撑管等组件,各个配合结构间均简化为简单的面接触,忽略法兰结构。本仿真中采用固体传热与表面对表面辐射耦合的多物理场,以稳态求解方式计算温度场的分布情况。

在稳态传热场中,定义在固体区域的温度方程为傅里叶定律的微分形式,即

(5)

(6)

式中:ρ为密度;cp为比定压热容;u为速度矢量;T为绝对温度;q为热传导通量;qr为辐射热流;Q为外加热源;k为导热系数。

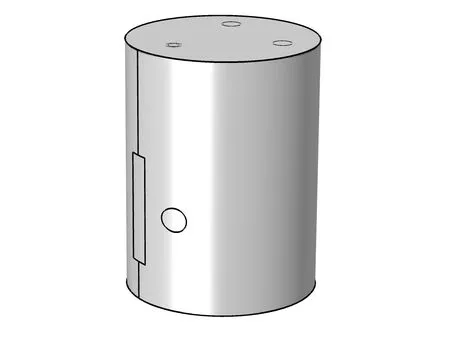
(a) 辐射屏

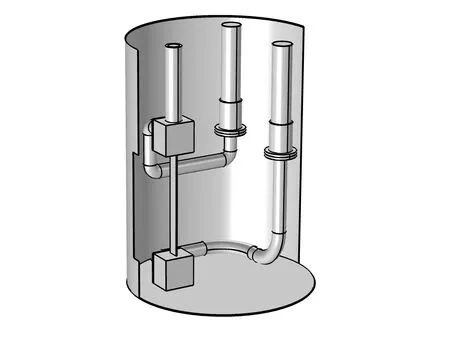
(b)辐射屏内部组件

辐射屏和二级冷头处的温度初始值分别为50、4.2 K。边界条件设置如下:考虑实际装置中支撑管上端面、内层石英玻璃、制冷机一级冷头均与辐射屏紧密接触,将其温度统一设置为50 K;二级冷头及其接触表面温度为4.2 K;制冷机冷头与热桥界面、夹具与热桥界面的热接触均设为等效热阻。计算中需要的材料的导热系数、密度、恒压热容等相关特性数据均来源于COMSOL软件中内置材料库,具体参数如表1所示。

初始温度为软件计算的多场耦合结果。边界条件分别设置如下:将试样表面、制冷机冷头表面、回热器表面、拉伸结构表面、玻璃表面以及辐射屏内表面分别设置为漫反射表面,均匀地向各个方向反射辐射强度,将辐射属性的波长相关性简化为常数,各表面的表面辐射率如表2所示。由于辐射屏内为真空环境,环境辐射率和散射辐照度均定义为0。辐射传热的计算方法为Hemicube(半立方体法),模型为稳态研究。通过表面对表面辐射传热耦合接口建立了传热-表面对表面辐射模型,分析了固体传热和辐射换热对温度场的影响。由于计算网格较密时,软件所需内存超出计算机内存能力,在满足网格独立性的基础上,本计算中将网格划分为24 264个。

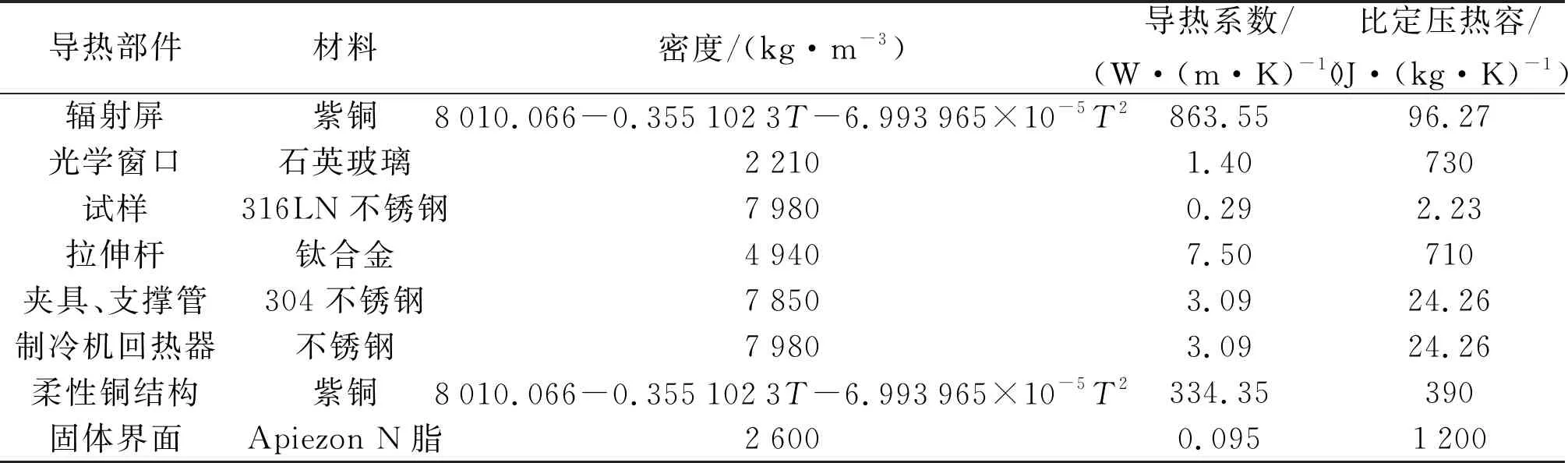
表1 COMSOL模型中材料的导热参数

表2 表面对表面辐射场中各个表面的辐射率[21-22]

2.2 Sage一维求解

对于辐射换热,Sage中两表面之间的辐射通过将它们连接至自带的辐射交换模型组件来实现建模,每个辐射面均以这种方式连接至其他辐射面并与之交换辐射。由于实际装置的模型的复杂度较高,因此对于低温力学拉伸装置中的局部结构特征,需要将其近似为Sage中可提供的模块。本装置结构转化为Sage模型的简化如下:装置中偏置的试样及拉伸组件在Sage中将采用与真空罩同轴的方式表达;在辐射换热计算中将拉伸组件统一视为一个整体,由于其形状复杂,简化为具有固定辐射面积的表面;初步假设室温端温度为300 K,试样、夹具、制冷机二级冷头等低温部件温度为4.2 K,辐射屏及其连接界面温度为50 K。

首先采用Sage计算导热传热量,根据上述装置的传热关系分析可知,参与导热的部件包括拉伸杆和支撑管,其材料、尺寸及传热参数如表3所示,Sage模型如图4所示。该模型为简单的固体传导,主要包括热端、冷端和导热体,导热体设置为一维导热。

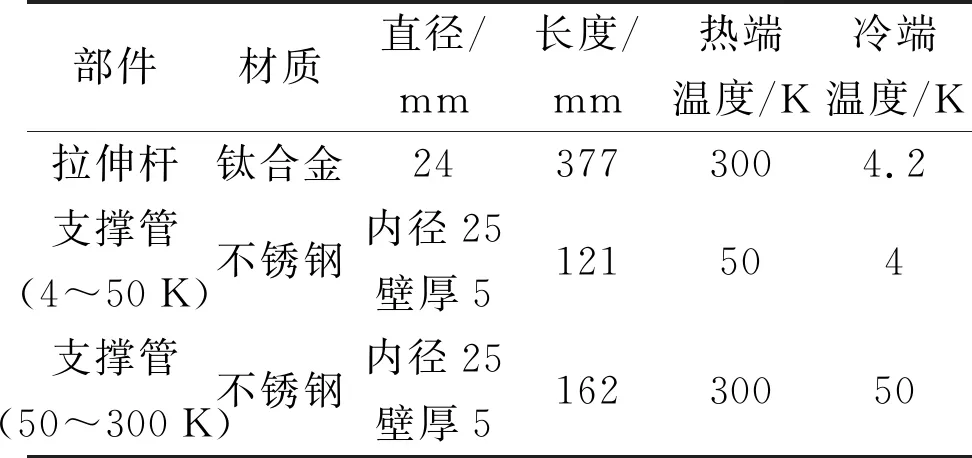
表3 导热部件尺寸及温度参数

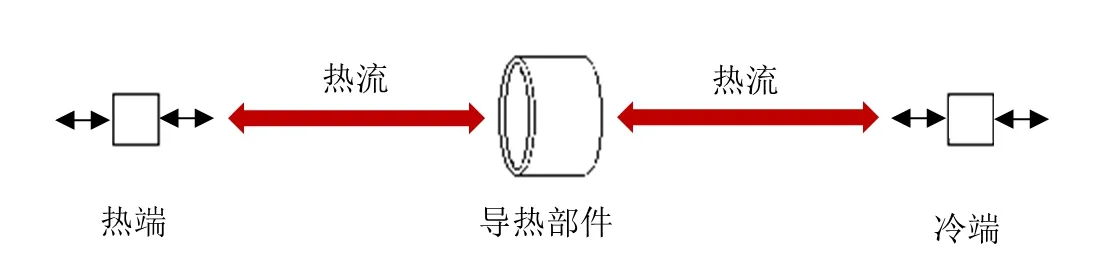
图4 低温拉伸装置中导热部件的Sage模型图Fig.4 Sage model of thermal conductive components in cryogenic mechanical testing device

各表面之间辐射换热的Sage模型均由热端、冷端和视图配置组件组成,视图配置组件根据两个相邻辐射表面的几何形状以及它们在空间中的相对方向在Sage自带的组件中选取,辐射换热的Sage模型如图5所示。视图配置组件汇总在子模块中。以辐射屏窗口与试样表面的辐射传热为例,图5(b)展示了子模块中辐射换热关系的基本结构,可以看出矩形窗口表面和圆形窗口表面为两个连接至热端点热源的辐射表面,试样表面连接至冷端点热源。假设试样表面与两窗口表面为平行放置,选取Sage中的平行表面组件,通过设置辐射流将辐射表面与组件连接。通过输入各表面计算参数,可计算出自热端表面至冷端表面的辐射换热量。计算过程中各表面的计算参数如表4所示。采用Sage计算时,共划分为420个节点。

(a)辐射屏窗口与试样的Sage辐射模型

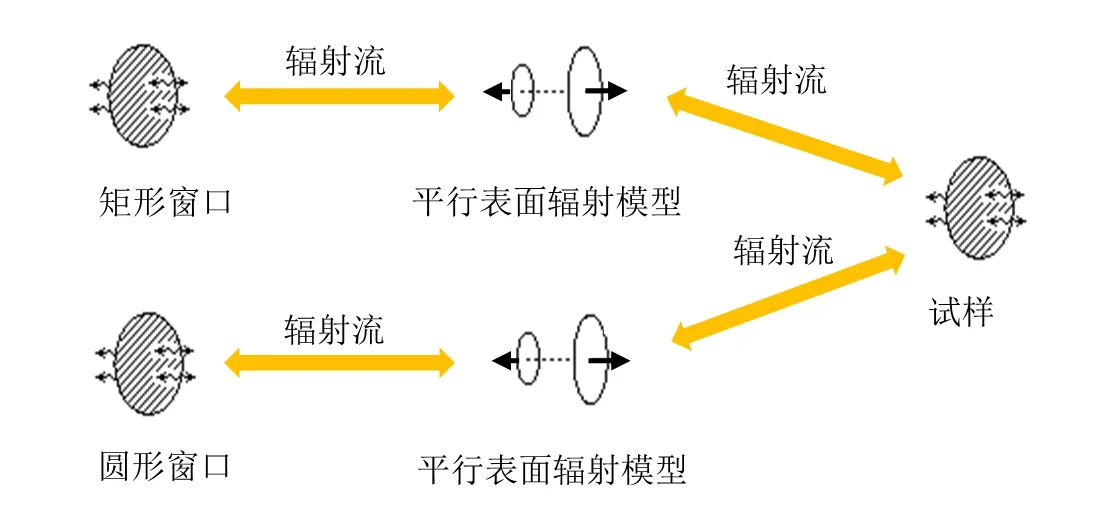
(b)辐射模型子模块的基本结构

表4 Sage辐射换热模型中采用的参数

根据上述计算的低温部件与外部环境的总换热量计算每个部件的热阻,还原部件自身因热阻产生的温差。

Apiezon N脂两侧的界面温差、导热部件两端温差为

(7)

(8)

式中:φ为换热量;A1-2为界面换热面积;A1为导热截面积;hAp为界面换热系数;λ为导热系数。

装置中的热阻如图6所示,图中C为冷头,tb1为热桥冷端,tb2为热桥热端,jig1为夹具冷端,jig2为夹具热端,Sam1为试样端部,Sam2为试样中部。热桥端部与其他部件的接触面之间界面换热系数hAp取1 835 W/(m2·K)[12]。部件的导热参数取平均温度对应的值,其结构参数与三维仿真中模型的取值相同。

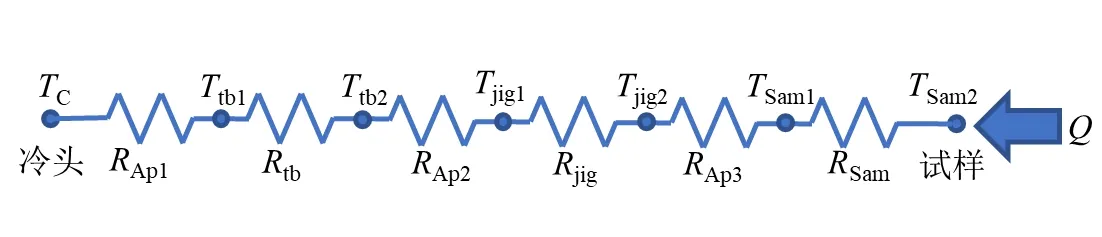
图6 低温力学拉伸装置内热阻简化图Fig.6 Simplified diagram of thermal resistance in the device

3 计算结果及讨论

对比分析了三维和一维求解方法对试样温度的计算结果,在保证计算精度的前提下,选择计算成本相对较低的一维求解方法分别计算了试样尺寸、试样表面发射率、窗口表面发射率和窗口尺寸对试样温度影响,为后续实验提供了参考。

3.1 三维求解方法与一维求解方法的计算结果对比

三维物理场计算结果如图7所示,导热部件的温度均呈线性分布,试样的两端温度为4.219 4 K,试样中部温度(最高温度)为9.676 5 K。

一维计算中,导热和辐射换热量如表5所示。从图1(b)可以看出,热阻计算中从试样至冷头的换热量为Qrad2-1+Qrad5,从夹具至冷头的换热量为Qrad2-1+Qrad5Qrad2-2+Qrad4。各部件或接触面间的温差如表6所示,试样自身的最低温度(即两端温度)、最高温度(即中部温度)分别为TSam1=4.211 5 K、TSam2=9.612 9 K。对比三维计算与一维计算的结果,可以看出两种计算结果几乎一致,认为在三维传热模型中可以将其解耦为各部件的一维传热单独计算,节约了计算时间,降低了操作难度。此外,由于一维计算中各部件被拆分为单独的模型,因此各部件的传热路径更加清晰,且传热参数更易提取。

(a)各部件的温度分布情况

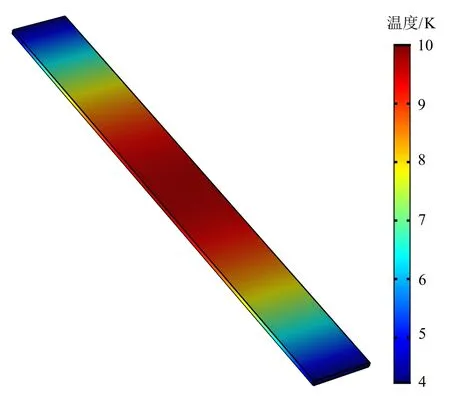
(b)试样温度分布

表5 Sage一维方法计算的制冷机二级冷头负载

表6 各温度节点间的温差

3.2 试样尺寸对其温度分布的影响

为进一步验证两种计算方法的一致性,保持其他结构参数不变,比较了3种不同尺寸的试样温度分布情况,其中试样1、2、3的尺寸分别取25 mm×230 mm×2 mm、12.5 mm×100 mm×2.5 mm和3 mm×30 mm×2.5 mm。试样尺寸对其温度的影响如图8所示,分别使用COMSOL、Sage计算的试样最低温度、最高温度,可以看出两种计算方法的结果基本吻合。3种尺寸的试样最低温度始终保持在4.20～4.22 K之间;最高温度却因尺寸不同有较大差别,试样1的最高温度高达约9.7 K,而试样3的最高温度最高约为4.4 K,说明试样尺寸是影响试样温度是否均匀的重要因素,且试样尺寸越小,其温度分布越趋于均匀。

根据图8中两种方法的结果,将其存在差异的原因总结如下:COMSOL通过三维几何模型可以将计算模型与实际装置中各部件的关系完好的呈现与匹配;而Sage的默认模型中只能根据各部件的关系选择较为合适的固有模型,在此基础上设置各参数的值。然而此装置中的很多部件与辐射屏为偏心放置,无法在Sage中匹配到完全适用的模型,故只能做近似处理与计算。COMSOL中将所有参与辐射换热的表面设置为漫反射表面,最终可获得综合辐射换热的结果;Sage中只考虑了各部件与辐射屏或光学窗口之间单独的辐射关系,而未将辐射屏内各部件之间的辐射关系考虑在内。

图8 试样尺寸对其温度的影响Fig.8 Effect of specimen size on specimen temperature

3.3 试样表面发射率对其温度分布的影响

由一维和三维计算方法的对比可知,两种方法的计算结果几乎一致,而Sage的计算时间和操作难度远小于COMSOL。因此,使用Sage研究了上述3种尺寸的试样在表面发射率分别为0.01、0.25、0.5、0.75以及0.95时试样的温度分布情况。试样尺寸与试样表面发射率对其温度的影响如图9所示,以试样1为例,随着试样发射率由0.95减小至0.01,试样最低温度由4.213 K降至4.202 K,降低幅度较小;而试样最高温度降低幅度较大,由9.799 K降至4.447 K。随着试样尺寸减小,表面发射率对温度的影响显著减小,其温度分布逐渐趋于均匀。试样3在发射率为0.01时,端部、中部温度分别为4.201、4.206 K,由此可见,在低温力学拉伸装置的实际使用中,减小试样尺寸和试样的表面发射率是使试样温度均匀分布的有效方法。

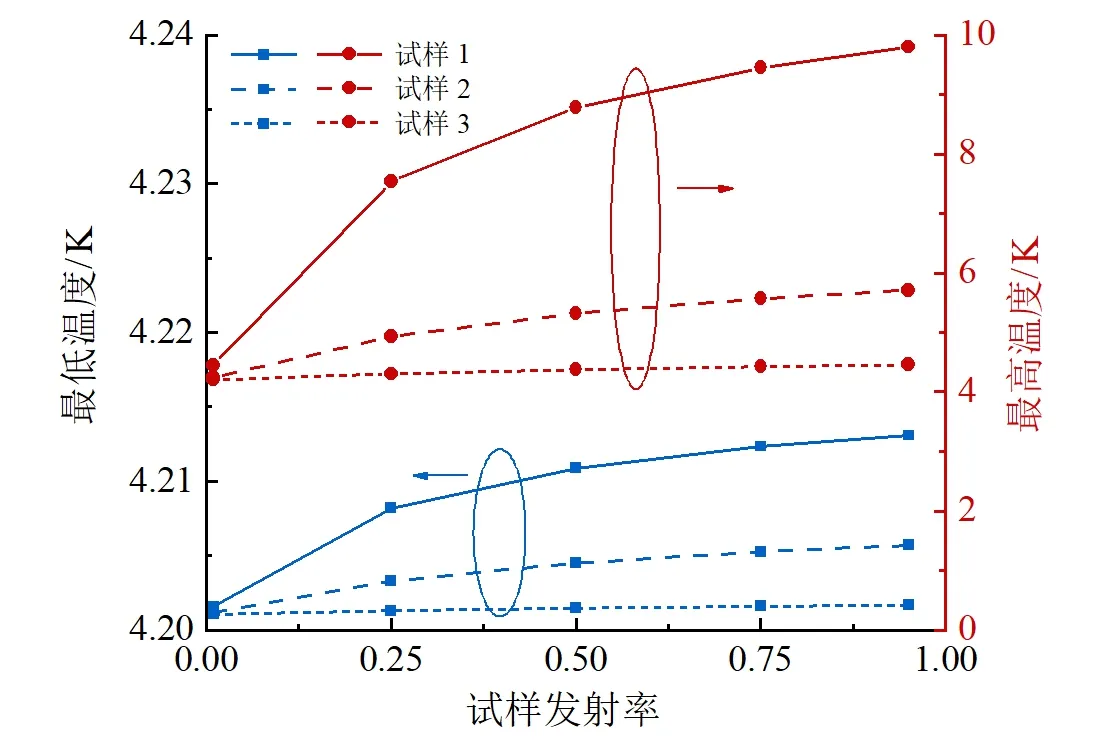
图9 窗口发射率为0.94时试样尺寸与试样表面发射率对其温度的影响Fig.9 The effect of sample size and specimen surface emissivity on its temperature for a window emissivity

3.4 窗口的表面发射率及其尺寸对试样温度分布的影响

使用Sage计算了窗口参数对3种试样温度分布的影响,其中试样的表面发射率均为0.95。玻璃窗口的表面发射率对试样温度的影响如图10所示,由图10可知:随着表面发射率由0.94降至0.01,试样1的自身温差由5.586 K降至3.195 K,尤其在窗口表面发射率从0.25降至0.01时,试样自身温差降幅显著;对于小尺寸试样3,试样自身温差始终保持最低,当窗口发射率为0.94时,试样自身最大温差仅为0.295 K。由此可见,降低窗口的表面发射率对大尺寸试样具有较为明显的效果,但小试样的温度分布几乎不受窗口表面发射率的影响。

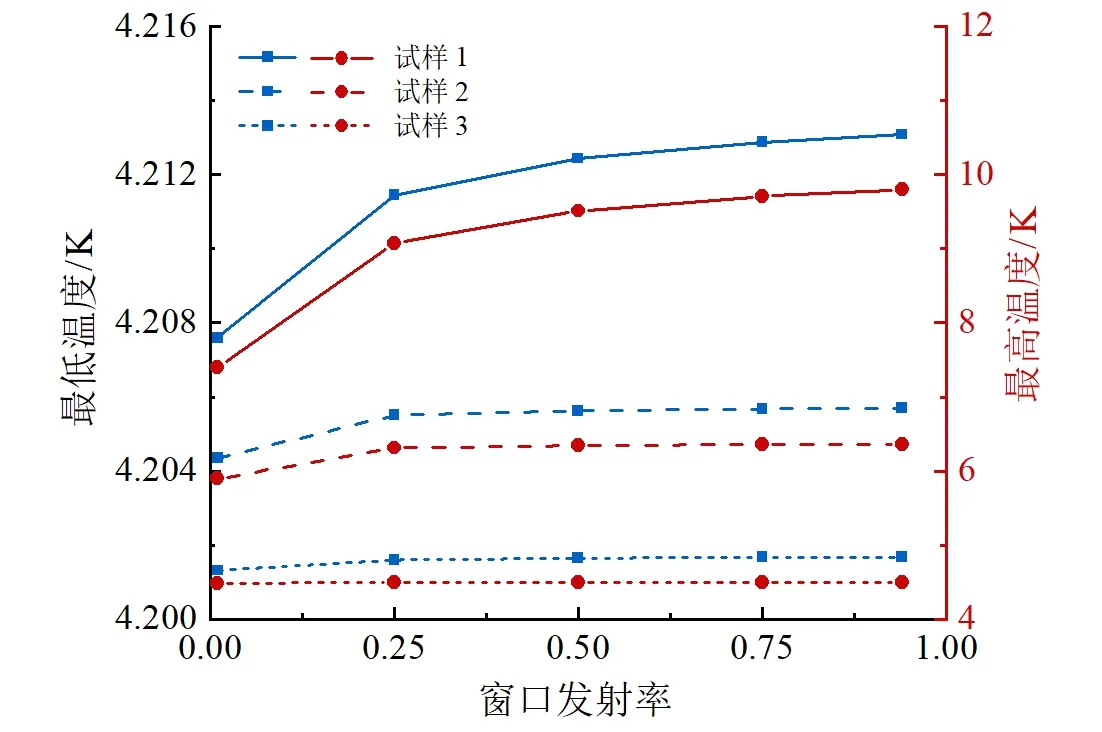
图10 试样发射率为0.95时窗口表面发射率对试样温度的影响Fig.10 Effect of window surface emissivity on sample temperature at sample emissivity of 0.95

窗口表面发射率为0.94、试样表面发射率为0.95时,窗口的有效辐射面积对3种试样温度的影响如图11所示。由图11可知,随着窗口的有效辐射面积增大,试样温度近似呈线性增长。随着窗口有效辐射面积由初始面积减小至初始面积的25%,试样1的自身温差由5.586 K减小至3.796 K,试样3的自身温差由0.294 K减小至0.264 K。因此,窗口的有效辐射面积对大尺寸试样的温度分布影响较大,对小尺寸试样几乎没有影响。

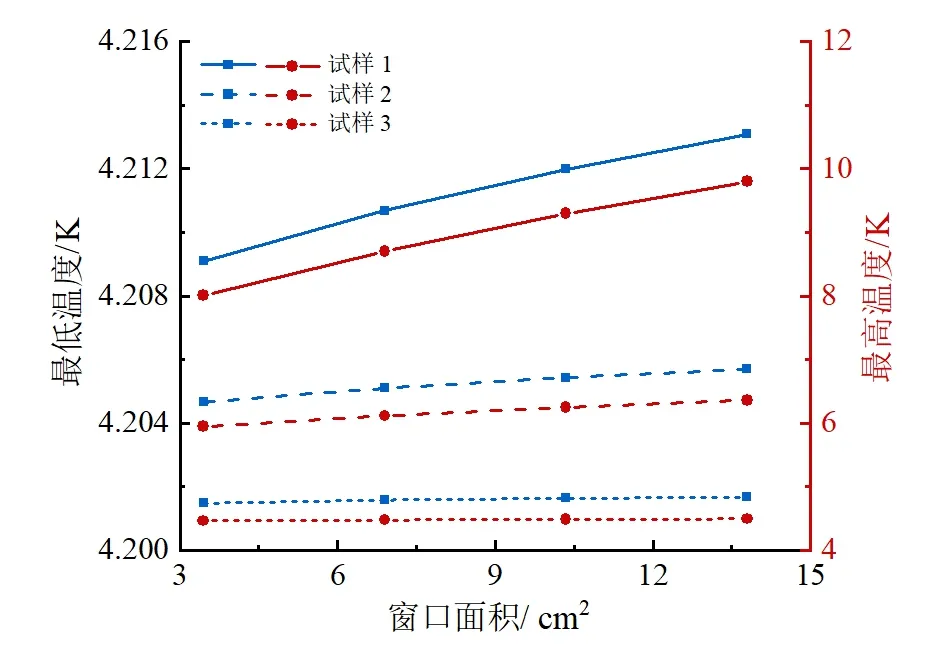
图11 试样发射率0.95、窗口发射率0.94时窗口有效辐射面积对试样温度的影响Fig.11 Effect of window effective radiation area on sample temperature for sample emissivity of 0.95 and window emissivity of 0.94

4 结 论

本文基于低温力学拉伸装置,分别使用COMSOL三维计算方法和Sage一维计算方法对装置中部件的传热情况进行了详细的数值研究,在此基础上对不同尺寸的试样温度进行了对比,最后研究了试样参数与窗口参数对试样温度分布的影响。得到如下主要结论。

(1)在相同的简化条件下,Sage一维计算方法与COMSOL三维仿真方法在传热计算与试样的温度场分析中得到的最低温度仅相差0.007 9 K,结果基本吻合。使用Sage软件建立的导热和辐射模型有助于对装置内的传热路径和热阻进行更为直观的分析。在传热场分析中,可以利用各部件间的空间关系选取Sage模块来代替复杂的三维耦合场计算,为低温装置的传热计算提供了新型计算方法与参考依据。

(2)对于大尺寸试样,将其表面发射率由0.95降至0.01后才可得到较为均匀的温度分布,自身温差由5.586 K降至0.245 K;随着试样尺寸减小,试样自身温度分布逐渐趋于均匀,对于本文中的小尺寸试样3(尺寸为3 mm×30 mm×2.5 mm),其自身温差几乎不受自身表面发射率的影响。

(3)随着窗口的表面发射率由0.94降至0.01,大尺寸试样1的自身温差由5.586 K降至3.195 K,而小尺寸试样3始终保持较为均匀的温度分布,其温差由0.295 K降至0.286 K。因此,小尺寸试样的温度分布几乎不受材料表面发射率和窗口参数的影响,且自身温差始终保持最小,满足实验要求。