基于最优方法的碰后辅助驾驶控制策略 *

2023-05-04魏佳宝吴晓建

汽车工程 2023年4期

周兵，魏佳宝，柴天，吴晓建，王鹤

（1.湖南大学，车身先进设计制造国家重点实验室，长沙 410082；2.南昌大学先进制造学院，南昌 330031）

前言

随着我国汽车保有量的增加，汽车事故也逐渐成为威胁人们生命与财产安全的重要原因之一［1］。汽车碰撞以及碰撞引发的二次碰撞是汽车事故中较为常见的情况，当车辆被撞后，往往会出现偏离车道、剧烈横摆等危险情况，极易导致二次碰撞甚至多次碰撞，严重威胁到驾乘人员的安全［2］，因此研究碰后的先进辅助驾驶技术对于保障驾乘人员安全具有重要意义。

面向汽车碰撞的先进辅助驾驶技术主要包括紧急避撞控制与稳定性控制等。在紧急避撞方面，Yuan等［3］基于模型预测控制统一了紧急避撞过程中的决策规划与控制问题，提升了车辆在应对避撞问题时的潜力。Cui 等［4］采用分阶段策略进行避撞控制，在第1 阶段控制车辆保持恒定的向心加速度进行转向避撞并且驶入相邻车道，同时采用差动制动来保证车辆稳定性；第2 阶段保持车辆行驶在相邻车道。Joseph 等［5］采用模型预测控制和反馈控制算法设计了新型控制框架，在避撞时可暂时忽视稳定性要求，从而在避撞时能够更充分地利用车辆性能。Jie 等［6］采用分层式结构，在路径规划层采用人工势场法规划避撞路径，在路径跟踪层采用多约束模型预测控制来计算前轮转角。

在稳定性控制方面，许男等［7］提出了新的车辆稳定性评价标准，在前后轮侧偏角相平面上计算稳定性指标，判断车辆的稳定性。Hou等［8］针对变附着系数路面，提出了一种分层转向控制策略。通过模糊控制适应路面附着系数和质心侧偏角的变化，并且在横摆力矩控制中通过滑模控制实现质心侧偏角与横摆角速度的综合控制。Wu 等［9］基于车辆质心侧偏角-质心侧偏角速度相平面提出了协调横摆角速度和质心侧偏角的动态权重系数，并且基于此动态权重系数提出了考虑控制目标变化的控制策略。

上述研究主要针对碰撞发生前的场景进行预警或控制，未考虑碰撞发生后对于被碰车辆的控制。Yang 等［10］针对车辆发生轻微碰撞的场景，在最优控制器中基于相对于初始碰撞发生位置的纵向和横向偏差设计了能够量化二次碰撞风险的代价函数，最终控制车辆停车。Di等［11］基于3 自由度车辆模型设计了次优2 阶滑模控制器，在跟踪期望的航向角与横向偏差方面相比1 阶滑模控制器具有更好的控制性能。Wang 等［12］针对四轮独立驱动车辆提出了碰后稳定性控制，首先通过滑模控制器计算恢复期望状态所需的附加横摆力矩，然后通过最优分配对前轮转角与四轮制动力矩进行分配。Wang 等［13］基于刚体碰撞模型提出了碰撞力估计模型，并且将模糊控制与PID 控制相结合控制车辆横摆角和相对于初始路径的横向位移。

以上研究对碰后车辆的控制做出了积极探索，但仍具有一定的局限性：（1）重视纵向和横向位移的最小化，但是却忽视了横摆稳定性，车辆容易出现失稳情况；（2）仅考虑了横摆稳定性，虽然能够控制车辆返回稳定域内，但是被碰车辆会产生较大的横向位移，容易发生二次碰撞；（3）虽然考虑了对横摆稳定性和横向位移的控制，但是对于控制量的分配却不够精确，不能充分发挥出轮胎纵向的力学性能。

针对这些问题，考虑到碰撞发生时普通驾驶员缺乏及时与正确的反应能力，参考宗长富等［14］对人机共驾技术中串联型双驾单控结构的研究，本文中提出一种碰撞后立即接管车辆驾驶权限的两阶段辅助驾驶控制策略。该策略在车辆发生侧向碰撞后默认驾驶员无法胜任驾驶任务，将强制接管驾驶权限。该策略分为两个阶段。在第一阶段中，通过分层控制使碰后车辆状态快速回归稳定域，并减小横向位移，以降低二次碰撞风险。综合车辆稳定性和横向位移两项指标设计了上层控制器的代价函数；下层控制器考虑前轮转角的影响设计了最优横摆力矩分配算法。然后依据相平面法所划分的稳定域制定切换准则，在判断车辆稳定后，控制系统切换至第2 阶段的路径跟踪控制，由模型预测路径跟踪控制器控制车辆驶回原车道，以减小对相邻车道的影响。

1 车辆动力学建模

1.1 整车动力学模型

配备线控制动执行器的过驱动车辆为碰后先进辅助驾驶技术的实现提供了更多可能，因此建立7自由度车辆动力学模型是进一步研究的基础。将悬架系统视为刚性系统，忽略由悬架引起的垂向运动、侧倾运动以及俯仰运动，建立合适的非线性7 自由度车辆模型，主要包括车辆的纵向运动、侧向运动、横摆运动以及4 个车轮的旋转运动。如图 1 所示，整车动力学方程如下。

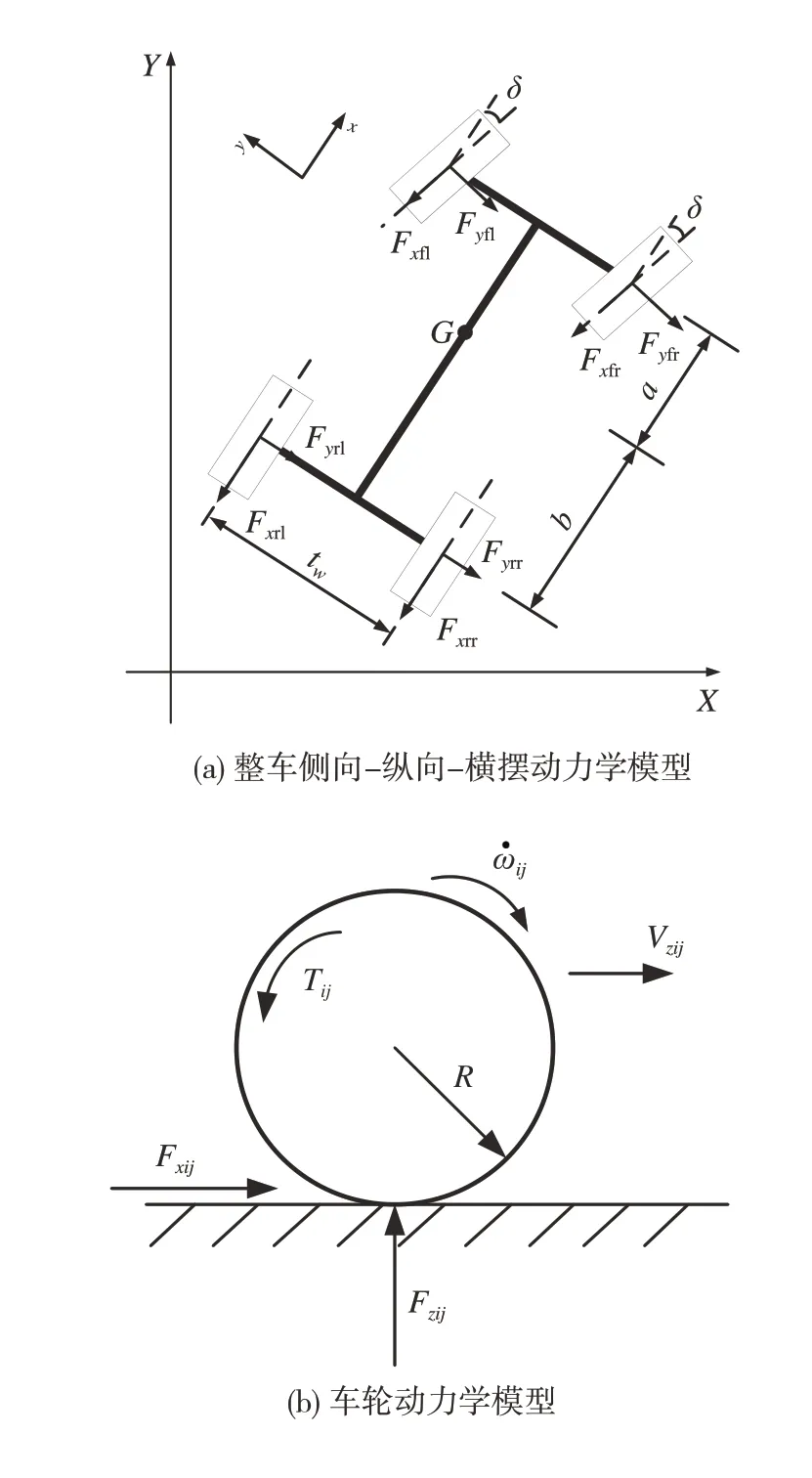
图1 车辆动力学模型

式（1）～式（12）中：m为整车质量（kg）；v、u分别是车辆在车身坐标系下沿x轴和y轴方向的速度分量(m/s)；Fxij、Fyij分别为地面施加给车轮的纵向力和侧向力（N），ij∈{fl，fr，rl，rr}分别表示车辆左前轮、右前轮、左后轮和右后轮，下文均采用此方式对车轮编号；δ为前轮转角（rad），这里忽略了阿克曼转角引起的左右前轮转角不一致性；φ̇为车辆横摆角速度（rad/s）；a、b分别为车辆质心到前、后轴的距离（m）；tw1、tw2分别为前、后轴的轮距（m）；Iz为车辆绕车身坐标系z轴的转动惯量（kg·m2）；Iw为车轮的转动惯量（kg·m2）；ωij分别为4个车轮的转速（rad/s）；Tbij分别为4 个车轮的制动力矩（N·m）；Tdij分别为4 个车轮的驱动力矩（N·m）；R为车轮滚动半径（m）。

1.2 轮胎模型

精确的轮胎模型将会提高车辆仿真的准确性。碰撞发生后，车轮侧偏角往往较大，车轮此时工作在非线性区，所以简单的线性轮胎模型已经不能满足需求，需要能够表现出轮胎非线性特性的轮胎模型。本文基于本团队之前的研究成果［15］，建立联合工况下的魔术轮胎公式［16］：

联合工况下，轮胎纵向力和侧向力存在耦合关系：

不同载荷下轮胎力与输入量的关系如图 2所示。

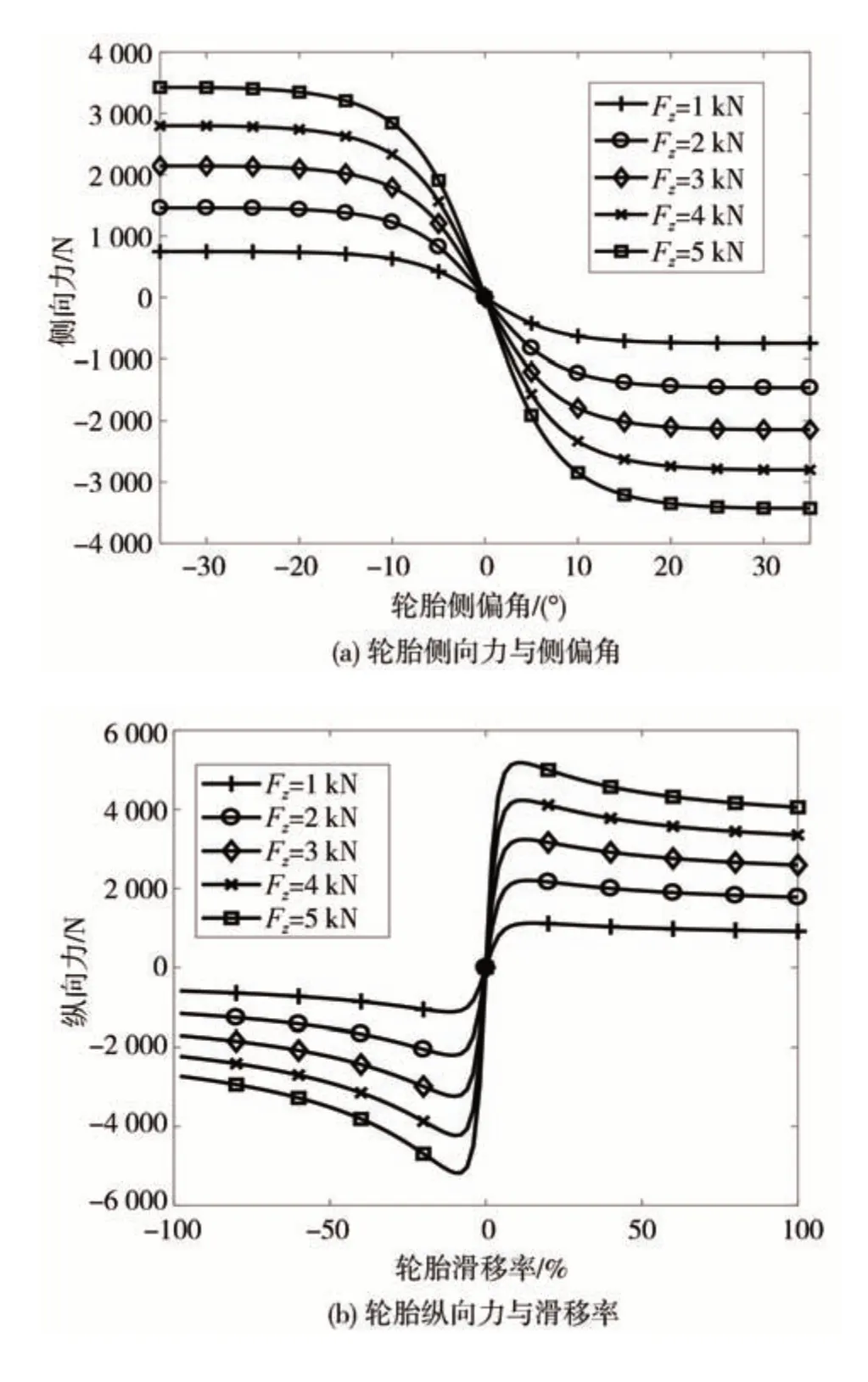
图2 不同载荷下轮胎力与输入量的关系

2 控制策略设计与算法实现

2.1 控制系统策略设计

本节将阐述车辆侧向碰撞场景以及发生碰撞后的控制策略。本文研究的侧向碰撞场景可简化为如图 3 所示，红色自车在双车道的右侧车道由西向东行驶，并且相邻车道没有其他车辆，在经过路口时与由南至北行驶的蓝色车辆发生碰撞。

图3 碰撞场景

需要说明的是，本文关注于碰撞发生后对目标车辆的控制，假设碰撞过程中没有碰撞损失以及碰后没有车辆故障。Yang 等在文献［17］中给出了目标车辆在纵向车速v= 15 m/s、横摆角Ψ= 0、路面附着系数μ= 0.9 的正常行驶状态下4 种具有代表性的碰后初始状态，如表 1所示。

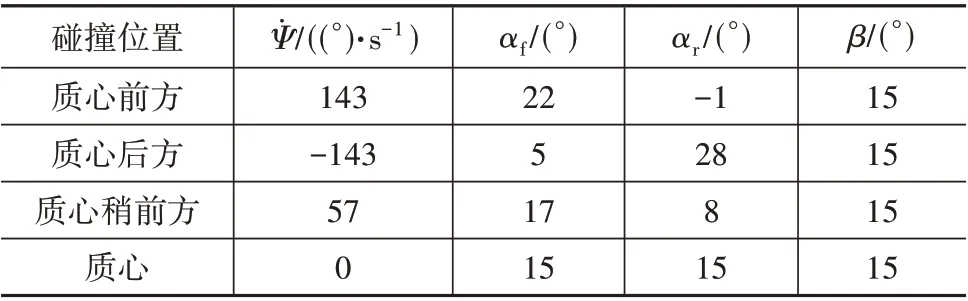
表1 被碰车辆常见状态

由表 1可见，车辆被碰后，状态将会发生剧烈变化，突然受到撞击的普通驾驶员基本难以应对此种紧急工况［18］，此类极端工况，有必要由控制器完全接管车辆驾驶权限。基于图 1 所示的碰撞场景分析，本文将碰后控制分为两个阶段，并根据两个阶段的车辆状态特点制定了不同的控制目标。

第1 阶段从自车被碰开始，以恢复车辆稳定性为目标，但是如果仅仅考虑车辆稳定性，可能会导致自车在回稳的过程中产生过大横向位移而与相邻车道发生碰撞，甚至行驶到道路边界线以外。因此也要兼顾车辆横向位移，直到车辆状态回归稳定域内为止。这样，避免了车辆在第1 阶段发生二次碰撞的同时，也为第2阶段尽快返回原车道做好准备。

第2 阶段从自车状态进入稳定域开始。为了减少主车对相邻车道的影响，控制器将控制车辆驶回原车道。系统结构图如图 4所示。

图4 系统结构图

综上，本文提出的两阶段控制器的控制目标有3 个部分：失稳状态下的横摆稳定性、最小横向位移和稳定状态下返回原车道。

2.2 第1阶段稳定性控制器

为简化控制器的复杂程度，第1 阶段采用分层控制。将前轮转角δ和附加横摆力矩Mz作为上层控制的输出量。模型预测控制算法通过权重矩阵协调不同的控制目标，能够求解出协调多个控制目标的最优解，能够满足上层控制器的设计需求。下层控制器则基于最优方法将附加横摆力矩Mz分配为4个车轮的制动力。

2.2.1 用于稳定性控制器的车辆模型

考虑控制目标与计算复杂度，忽略其他次要因素，将车辆简化为一个只有侧向运动与横摆运动的线性2 自由度单轨车辆动力学模型。用于第1 阶段上层控制器设计的状态空间方程为

其中：状态向量ξt1=[y，ẏ，φ，φ̇，X，Y]T

控制量ut1=[δ，Mz]T；输出向量ηt1=[φ，φ̇，Y]T

式中：y(m)是车辆在车身坐标系下的横向位移；ẏ（m/s）是车身坐标系下的横向速度；φ(rad)是车辆的横摆角；φ̇(rad/s)是车辆的横摆角速度；X(m)是车辆在大地坐标系下的纵向位移；Y(m)是车辆在大地坐标系下的横向位移；δ(rad)是前轮转角；Mz(N·m)是附加横摆力矩；Ccf、Ccr分别是前、后轮的线性侧偏刚度。

利用前向欧拉法对该连续系统进行离散，其中ts1为采样时间，得到离散状态空间方程：

其中：Ad1=At1ts1+I；Bd1=Bt1ts1；Cd1=Ct1

2.2.2 第1阶段上层控制器目标函数

在传统稳定性控制中，通常将理想2 自由度车辆模型作为参考模型［19］，将由理想2 自由度车辆模型得到的质心侧偏角和横摆角速度作为期望状态量。然而在碰后控制中，车辆受到冲击力的作用，状态发生突变，此时普通驾驶员的操作可能对恢复稳定性并没有参考意义，因此本文设计的稳定性控制器以车辆正常直行时的状态量作为期望状态量。车辆横摆角和横摆角速度表征了车辆的横摆稳定性［20］，因此将横摆角和横摆角速度作为第1 阶段的被控量。两者的期望值都为零，即：φr1= 0；φ̇r1= 0。

在恢复被碰车辆稳定性的同时，应尽量减少被碰车辆的横向位移，以避免二次碰撞的发生。以碰撞发生点为坐标原点建立大地坐标系，第1 阶段控制器的期望横向位移为零，即：Yr1= 0。

构建目标函数如下：

式中：期望状态向量ηr1=[φr1，φ̇r1，Yr1]T；U1=[δ，Mz]T；第1项是对期望状态量的跟踪；Qη是期望状态量的权重系数矩阵；第2 项对应于对控制增量的平滑；R是惩罚系数矩阵；第3 项中ε1为约束边界的松弛因子［21］，保证优化问题存在可行解；ρ1为松弛因子的权重系数。

当车辆处于第1 阶段时，轮胎往往工作于非线性区域，此时前轮转角增大，前轮侧向力并不会随之线性增长，所以前轮转角对于车辆的控制作用较小，而差速制动通过改变轮胎的纵向力实现对车辆稳定性的控制。通过权重矩阵QU协调两种控制量的控制作用。构建目标函数为

式中：Np和Nc分别为模型预测控制器的预测时域和控制时域；u1min和u1max分别为控制量的最小值和最大值约束；Δu1min和Δu1max分别为控制增量的最小值和最大值约束。

2.2.3 下层期望横摆力矩最优分配器

为了充分利用车辆4 个轮胎的制动力，本文采用最优分配的方式实现制动力的分配。目标函数为

式中δ为上层控制器计算出的前轮转角。当Mzr为正值时，表示其方向为绕车辆z轴逆时针旋转，Mzr为负值时，表示其方向为绕车辆z轴顺时针旋转。Fbi为待求解的轮胎纵向力，i∈{1，2，3，4}。

路面附着系数决定了车轮能够利用的最大纵向力，由轮胎摩擦圆可知

综合式（22）-式（25）得到期望横摆力矩最优分配控制器：

2.3 第2阶段路径跟踪控制器

在车辆状态进入稳定域后，控制目标转变为驶回原车道。基于模型预测控制算法设计了路径跟踪控制器。

2.3.1 用于路径跟踪控制器的车辆模型

第2 阶段车辆动力学模型与第1 阶段的不同之处在于状态转移方程的控制量与输出量，这里仅详细列出不同部分。状态空间方程如下：

其中：Ad2=At2ts2+I；Bd2=Bt2ts2；Cd2=Ct2

2.3.2 第2阶段目标函数

第2 阶段控制器的控制目标是驶回原车道，减少碰撞对临近车道的影响。这里取第2 阶段控制器的期望状态为φr= 0，Yr= 0。

构建目标函数如下：

需要注意的是，控制器切换时，可能会引起控制量的突变，这里指前轮转角的突变。因此，需要将切换前第1 阶段控制器求解的前轮转角作为第2 阶段控制器的初始解，以保证控制量的平滑变化。

2.4 控制器切换准则

2.4.1β-β̇相平面

相平面法可以很好地解决车辆稳定性判定的相关问题［22］。考虑到被碰后的车辆表现出强烈的非线性，因此这里采用基于质心侧偏角-质心侧偏角速度即β-β̇相平面法所划定的稳定域边界作为控制器切换准则。考虑车辆横摆运动和侧向运动，建立非线性2自由度车辆模型，即

对式（31）在不同的初始条件β(0)和φ̇(0)下给定前轮转角和车速，建立的β-β̇相平面如图 5所示。

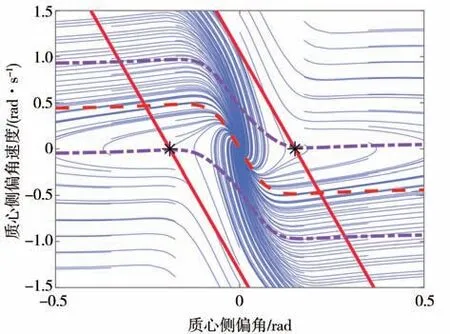
图5 相平面及其稳定域边界

2.4.2 相平面划分准则

一般根据相轨迹最终收敛的状态将相平面划分为稳定域和非稳定域。稳定域由收敛于平衡点的多条相轨迹构成，非稳定域由发散的多条相轨迹构成［23］。参考余卓平等［24］对相平面划分的研究，建立车辆稳定域，即

式中：kβ为通过仿真试验获得的稳定域边界斜率；βl，0和βh，0分别为相图左右两侧鞍点的横坐标；和分别为横摆角速度的上下限值。左右边界如图 5中红实线所示，上下边界在相平面中如图 5 紫色点画线所示。

在实际运用中，为了快速得到不同车速、转角与路面附着系数的相平面边界，可以建立相应的映射表，通过查表的方式实时得到相平面边界。

利用车辆状态与稳定域边界的关系建立两阶段控制器的切换准则。当车辆状态在稳定域外时，第1 阶段控制器发挥作用，当车辆状态进入稳定域后，如果继续跟踪第1 阶段的期望状态量，将会导致附加横摆力矩持续作用，这对车速、乘坐舒适性等产生较大影响，不利于第2阶段的控制。因此第2阶段控制器只控制前轮转向实现驶回原车道的控制目标。

3 仿真分析

为验证本文所提出的碰后辅助驾驶控制策略的有效性和性能，基于Matlab/Simulink 平台搭建了车辆模型和控制器模型，并进行多种碰撞工况下的仿真分析。车辆动力学模型参数来自于Carsim BClass 车辆模型，如表 2 所示。两阶段控制器的参数如表 3所示。仿真结果如图6和图7所示。

图6 仿真工况1结果对比

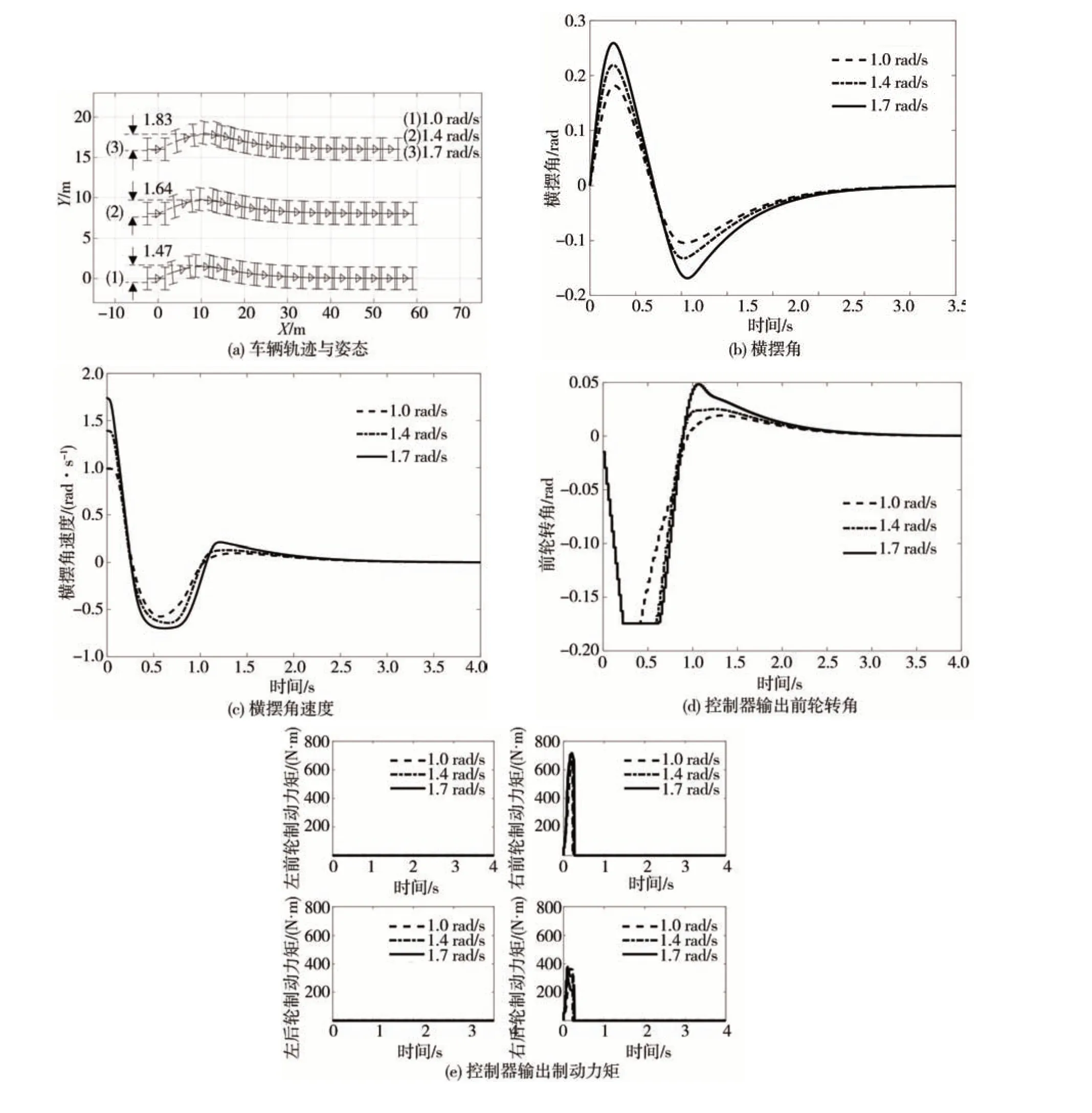
图7 仿真工况2结果对比

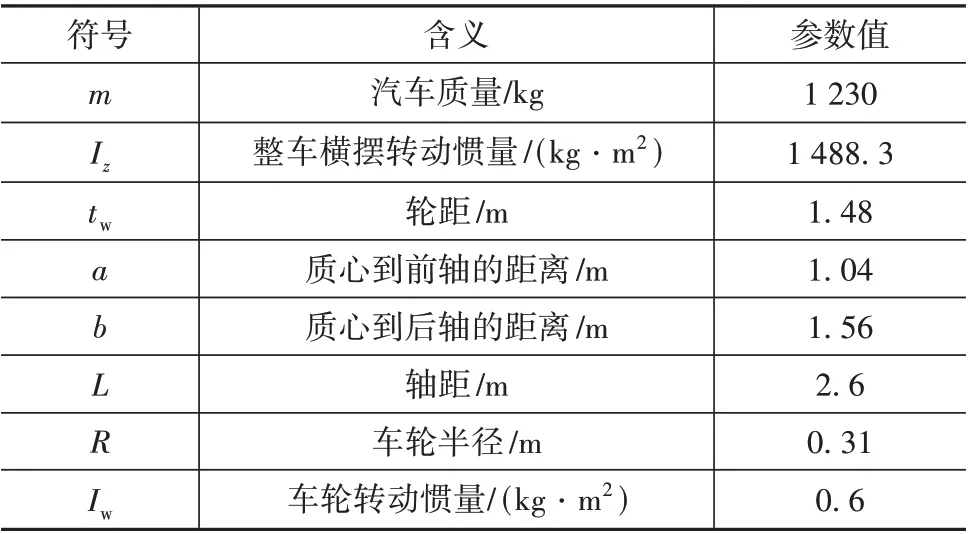
表2 车辆参数

表3 控制器参数

3.1 仿真工况1

设置主车被碰前的车速为15 m/s，路面附着系数为0.85，以表1 中质心前方轻碰的车辆状态作为主车被碰后的初始状态，与无控制、全制动、仅控制横摆稳定性、仅控制横向位移4 种仿真工况进行对比，验证本文提出的碰后控制的有效性。

图 6 为仿真工况1 的对比结果。结合图 6（a）-图 6（c）可以看出，两阶段控制能够在车辆被碰后0.26 s左右将车辆的横摆角速度降至0，此时车辆横摆角达到最大值，但是车辆仅产生5 m的纵向位移和1 m的横向位移。在此之前，其轨迹与其他控制方式下的车辆轨迹没有明显区别的原因在于此时车辆前轮处于非线性区域，前轮转角对车辆轨迹的控制作用较小。两阶段控制的最大的横向位移仅有1.4 m，随后便逐渐控制车辆恢复到原车道行驶，其横摆角和横摆角速度与仅控制横摆稳定性的横摆角和横摆角速度在第1阶段内十分接近，具有明显的控制效果。无控制的车辆横摆角保持在较大值，最终也冲出道路。四轮制动车辆的行驶距离最短，但是其横向位移明显将会冲出车道。仅控制横摆稳定性的车辆航向角较大，并且横向位移持续增大。仅控制横向位移的车辆横摆角和横摆角速度出现较大波动，说明车辆未能及时稳定。图6（f）和图6（g）展示了两阶段控制中各个车轮纵向力和侧向力的变化曲线，其中右前轮和右后轮的纵向力变化趋势与图6（e）中的一致。

当然，在两阶段控制下，能够观察到第2 阶段时车辆的横摆角和横摆角速度有一定的波动，但此时车辆已经进入稳定域，小波动的横摆角和横摆角速度是由于第2 阶段控制器将车辆引导回原车道时产生的，并不会影响车辆的稳定性。

3.2 仿真工况2

为了进一步验证本文提出的碰后控制的性能，在初始车速与路面附着系数不变的情况下，车辆被碰后的横摆角速度分别设为1、1.4、1.7 rad/s，对3 种不同的初始横摆角速度工况进行仿真。

图 7 为仿真工况2 的对比结果。从图7（a）中可以看出，随着车辆被碰后初始横摆角速度的增加，车辆的最大横向位移逐渐增加，但其最大值也没有超过1.9 m，对车辆被碰后的横向位移能够起到较好的控制作用。从图7（b）和图7（c）中可以看出，两阶段控制器在3 种工况下的第1 阶段都能及时对车辆的横摆角和横摆角速度产生控制作用。从图7（d）中可以看出，3 种工况下，第1 阶段的前轮转角控制量基本一致，说明本文提出的控制器具有较好的鲁棒性。从图7（e）中可以看出，随着初始横摆角速度的增加，车辆右侧两个车轮的制动力响应也逐渐加快，说明两阶段控制器能够适应不同强度的碰撞。

3.3 硬件在环实验

为验证本文所提出的碰后辅助驾驶控制策略的实时性，基于dSpace 平台开展了硬件在环实验。实验设备如图 8 所示，包括SCALXIO、DS1401/1513 MicroAutobox II和Break-Out Boxes等。

图8 硬件在环平台

车辆模型运行在SCALXIO 中，控制策略运行在DS1401/1513 MicroAutobox II 中，通过CAN 通信实现控制器与车辆模型的通信。模型在环（MIL）与硬件在环（HIL）结果对比如图 9所示。

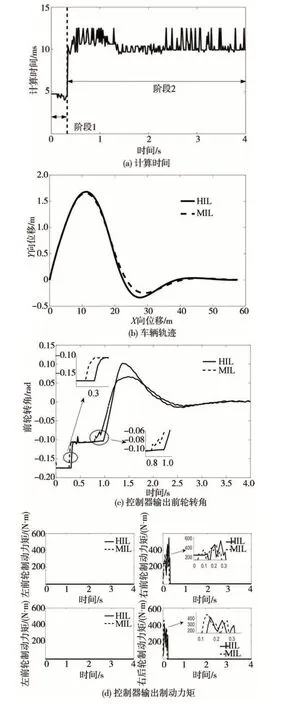
图9 模型在环与硬件在环实验结果对比

硬件在环实验平台中运行的碰后工况与仿真工况1 相同。图9（a）表明碰后控制策略的第1 阶段计算时间为5 ms左右，第2阶段的计算时间为10 ms左右，满足车辆控制的实时性要求。图9（b）-图9（d）表明硬件在环实验具有与模型在环相近的运行结果，但是由于CAN 通信，硬件在环实验存在一定的延迟。总之，硬件在环实验验证了所提出的碰后控制策略的良好性能。